数据结构之算法的时间复杂度和空间复杂度
本章重点:
1.算法效率
2.时间复杂度
3.空间复杂度
4. 常见时间复杂度以及复杂度oj练习
目录
1.算法效率
1.2算法的复杂度
2.时间复杂度
2.1 时间复杂度的概念
2.2 大O的渐进表示法
2.3常见时间复杂度计算举例
3.空间复杂度
4. 常见复杂度对比
5.复杂度的oj练习
5.1消失的数字
5.2旋转数组
1.算法效率
1.1 如何衡量一个算法的好坏
如何衡量一个算法的好坏呢?比如对于以下斐波那契数列:
long long Fib(int N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}斐波那契数列的递归实现方式非常简洁,但简洁一定好吗?那该如何衡量其好与坏呢
1.2算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般
是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算
机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计
算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
2.时间复杂度
2.1 时间复杂度的概念
可以将算法的时间复杂度看成是一个函数,类似于一个函数式子 F(N) = N,算法中的基本操作的执行次数,为算法的时间复杂度。即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}这个函数执行的基本操作次数:可以用函数式子
来表示当N 变化时候
N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010
对应的函数结果是不同的 那怎么衡量他的时间复杂度呢?实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法
2.2 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
2.3常见时间复杂度计算举例
实例1:
// 计算Func2的时间复杂度?
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}最差情况下 运行 2N + 10 大O渐进法 去掉影响因素较小的 以及系数,所以时间复杂度为O(N)
实例2:
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}
printf("%d\n", count);
}这个程序中并没有介绍M 和N 的大小 所以时间复杂度为O(M + N).
实例3:
// 计算Func4的时间复杂度?
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}所有常数的时间复杂度都可以优化到O(1)。
实例4:
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, int character );寻找字符串函数 最差情况就是O(N)
实例5:
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}最好的情况下:是顺序的 只需要两两比较,只需要O(N),如果不是有序的 需要每个比较 那就是O(N方)
实例6:
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n-1;
while (begin < end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid;
else
return mid;
}
return -1;
}二分查找,前提是有序 就像折纸一样,最悲观的情况 1 * 2 *2 *2 .......x = N 总共运行了x次
根据指数公式 x =
实例7:
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{
if(0 == N)
return 1;
return Fac(N-1)*N;
不为零 就要运行一次 一直运行到N = 0; 一共N + 1次 去掉没用的那就是O(N)
实例8:
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}
悲观计算法 时间复杂度 就是O(N)
3.空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用额外存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因
此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定
实例1:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
额外变量只有一个 所以空间复杂度是O(1)
实例2:
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if(n==0)
return NULL;
long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}额外申请了n+ 1 个空间 所以空间复杂度为O(N)
实例3:
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{
if(N == 0)
return 1;
return Fac(N-1)*N;
}递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
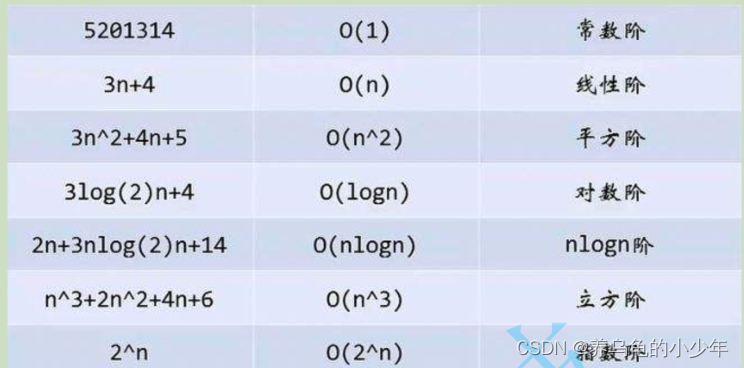
4. 常见复杂度对比
5.复杂度的oj练习
5.1消失的数字
#include<stdio.h>
// 利用异或的知识点,交换律不改变最终结果,所以 定义一个变量 初始值为0,与数组异或后,在与给定数组异或,剩下的值就是我们要找的
int missingNumber(int* nums, int numsSize)
{int x = 0;for (int i = 0; i <= numsSize; i++)// 不缺失,所以正常数组大小比给定数组大小大1{x ^= i;}for (int i = 0; i < numsSize; i++){x ^= *(nums + i);}return x;
}
int main()
{int nums[100] = { 0 };int num = sizeof(nums) / sizeof(nums[0]);for (int i = 0; i < num; i++){scanf("%d", nums[i]);}printf("%d", missingNumber(nums, num));return 0;
}5.2旋转数组
// 先封装一个转置函数
void reverse(int* pa, int left, int right)
{while (left < right){int temp = 0;temp = *(pa + left);*(pa + left) = *(pa + right);*(pa + right) = temp;++left;--right;}
}void rotate(int* nums, int numsSize, int k)
{if (k >= numsSize){k %= numsSize;}// 将前 numsSize - k - 1 个数 转置reverse(nums, 0, numsSize - k - 1);// 将后 k 个数 转置reverse(nums, numsSize - k, numsSize - 1);// 将整体转置 个数 转置reverse(nums, 0, numsSize - 1);}
相关文章:

数据结构之算法的时间复杂度和空间复杂度
本章重点: 1.算法效率 2.时间复杂度 3.空间复杂度 4. 常见时间复杂度以及复杂度oj练习 目录 1.算法效率 1.2算法的复杂度 2.时间复杂度 2.1 时间复杂度的概念 2.2 大O的渐进表示法 2.3常见时间复杂度计算举例 3.空间复杂度 4. 常见复杂度对比 5.复杂度…...

【微信小程序】使用页面跳转并携带多个特定参数
前言在我们项目的搭建时常常会用到页面跳转,在微信小程序中也支持多个跳转类型。如(wx.switchTab\wx.reLauch\wx.redirectTo\wx.navigateTo\wx.navigateBack)等等,每一个路由API都是有相对应的特定跳转功能,在这里我就不赘述了。微信开发者文…...

CVPR 2021 | Involution:超越convolution和self-attention的神经网络算子
CVPR 2021 | Involution:超越convolution和self-attention的神经网络算子 论文地址:https://arxiv.org/pdf/2103.06255v2.pdf 代码地址:https://github.com/d-li14/involution Involution卷积,文章描述说它比convolution更轻量更高效,形式上比self-attention更加简洁,可以…...
11 OpenCV图像识别之人脸识别
文章目录1 Eigenfaces1.1 建模流程1.2 示例代码2 Fisherfaces2.1 建模流程2.2 示例代码3 Local Binary Histogram3.1 建模流程3.2 示例代码OpenCV 提供了三种人脸识别方法:Eigenfaces Eigenfaces是一种基于PCA(Principal Component Analysis,…...
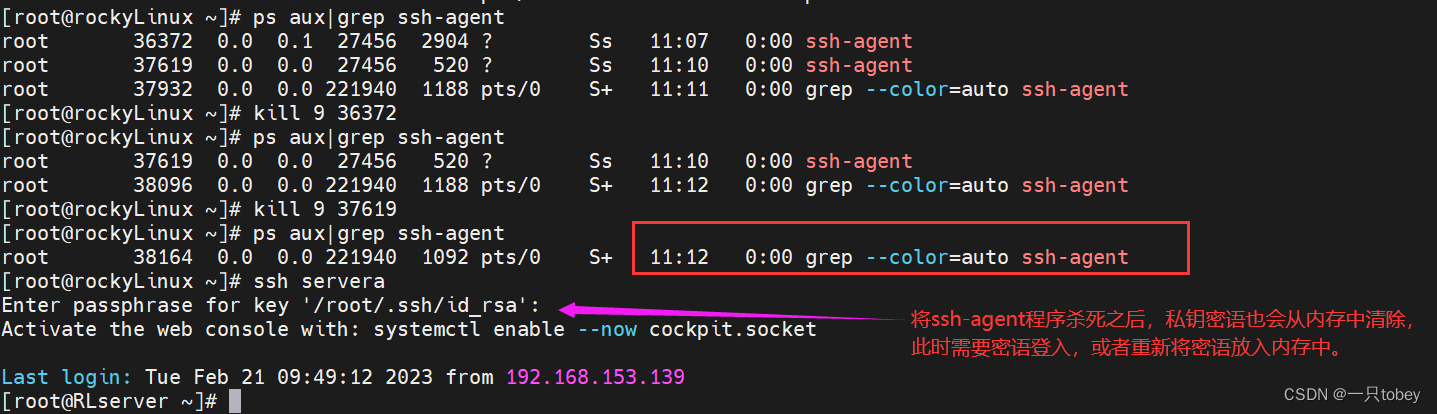
ssh设置:免密登入、修改默认端口、禁止root登入、限制错误登入次数
服务器: 客户端: 在下面不再说明服务器和客户端。 1.修改ssh默认端口 是在服务器中设置。 该设置涉及三部分:sshd配置文件修改/增加新端口、Selinux添加新端口、Firewall开放新端口。 vim /etc/ssh/sshd.config,找到#Port行&…...
【Fastdfs】| 入门连续剧——安装
作者:狮子也疯狂 专栏:《spring开发》 坚持做好每一步,幸运之神自然会降临在你的身上 目录一. 🦁 前言Ⅰ. 🐇 为什么要使用分布式文件系统?1.1 单机系统 vs 独立文件服务器1.2 分布式文件系统1.3 FastDFS引…...
【ESP32-S3】Pycharm 使用 microPython 教程(避坑)
一、下载Pycharm等操作 1.百度云下载链接 链接:https://pan.baidu.com/s/1tkbMzS5B_v-Cn4WQlTqS3Q?pwd0108 提取码:0108 2.安装 按照压缩包中的教程来,你懂的。 二、配置microPython环境 1.安装 microPython 插件 1.1 File > Sett…...
Allegro如何通过报表的方式检查单板上是否有假器件操作指导
Allegro如何通过报表的方式检查单板上是否有假器件操作指导 在做PCB设计的时候,输出生产文件之前,必须保证PCB上不能存在假器件,如下图,是不被允许的 当PCB单板比较大,如何通过报表的方式检查是否存在假器件,具体操作如下 点击Tools点击Reports...
清理bib文件(删除重复项,仅保留tex中引用的条目)
在写latex文件的过程中,经常会遇到添加了一堆文献的bibtex到bib文件中,有时候文章一长同一篇文献用不同的cite-key引用了多次,同时也会有一些文献最后并没被正文引用,这就需要对bib文件进行清理。 删除重复项 可以用JabRef 在J…...

Rust编程细节知识点拾遗
1.Rust中每一个引用都有生命周期,也就是引用保持有效的作用域。生命周期主要目标是避免悬垂引用,悬垂引用就是引用了已经释放的值。函数中,x的生命周期不能小于返回值得生命周期。当有x和y的时候,两者的生命周期是两个里面较小的那…...

【Linux】线程池
🎇Linux: 博客主页:一起去看日落吗分享博主的在Linux中学习到的知识和遇到的问题博主的能力有限,出现错误希望大家不吝赐教分享给大家一句我很喜欢的话: 看似不起波澜的日复一日,一定会在某一天让你看见坚持…...

运动版蓝牙耳机什么牌子的好、运动款蓝牙耳机推荐
何以解忧?唯有运动。事实已经无数次证明,运动不但可以让你更瘦身、更紧实,更重要的是精神状态也能焕然一新。不知道各位是不是也跟我一样,喜欢在运动的时候听着音乐。但是听音乐就需要有好的续航,否则运动一半没电了&a…...
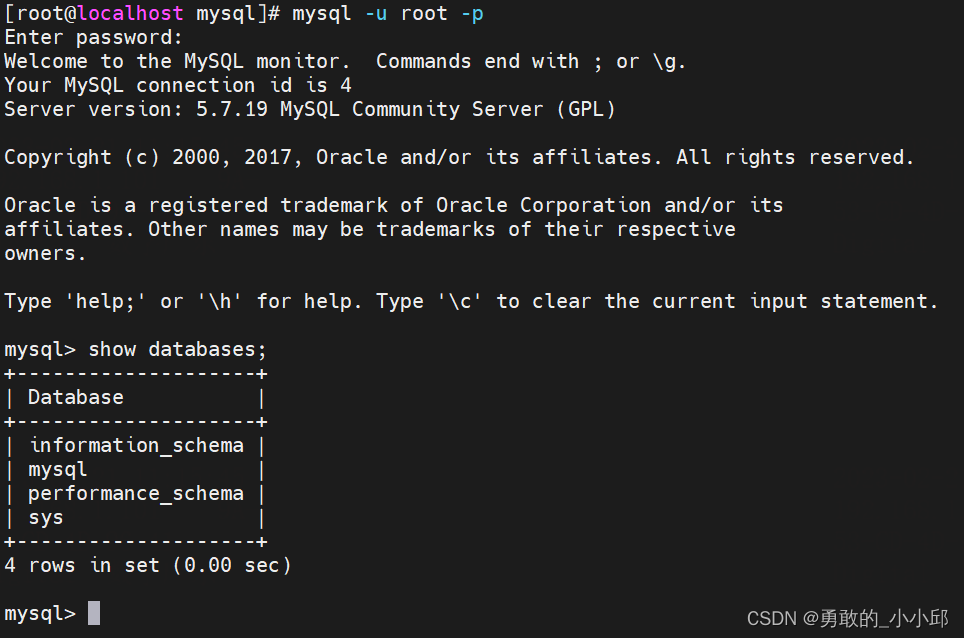
MySQL中自带的数据库表相关介绍
mysql的自带数据库表主要有以下几个: (1)information_schema (2)performance_schema (3)mysql (4)sys (5)可能存在空数据库test 一、informa…...

【微信小程序】--注册小程序账号(一)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &#…...

Java多线程 - 利用Callable或CompletableFuture实现多线程异步任务执行
文章目录1. Callable接口源码2. Future接口的源码3. RunnableFuture接口和FutureTask实现类4. 利用线程池和Callable接口实现异步执行任务5. 利用CompleteFutable实现多线程异步任务执行1. Callable接口源码 FunctionalInterface public interface Callable<V> {// 这个…...

【ts + webpack】贪吃蛇小游戏
目录 一、项目搭建 1.1 初始化项目 二、项目界面布局 三、完成Food类 四、完成记分牌类 五、初步完成snake类 六、创建游戏控制器类 - 键盘事件 七、GameControl - 使蛇移动 八、蛇撞墙和吃食检测 一、项目搭建 1.1 初始化项目 1.使用init命令生成package.json文件 …...

传统巨头生“变”,中国毫米波雷达市场战火再升级
进入2023年,中国车载毫米波雷达市场战火明显升级。 一方面,愈演愈烈的份额抢夺战不仅仅存在于几大传统巨头之间,也快速转移到与国产供应商之间;随着部分外资巨头的本土化战略深入落地,同时对国产供应商造成了压力。 …...

26岁曾月薪15K,现已失业3个月,我依然没有拿到offer......
我做测试5年,一线城市薪水拿到15K,中间还修了一个专升本,这个年限不说资深肯定也是配得上经验丰富的。今年行情不好人尽皆知,但我还是对我的薪水不是很满意,于是打算出去面试,希望可以搏一个高薪。 但真到面…...

华为OD机试 - 打印文件 | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 简易压缩算法(Python) | 机试题算法思路 【2023】 华为OD机试题 - 获取最大软件版本号(JavaScript) 华为OD机试 - 猜字谜(Python) | 机试题+算法思路 【2023】 华为OD机试 - 删除指定目录(Python) | 机试题算法思路 【2023】 华为OD机试 …...
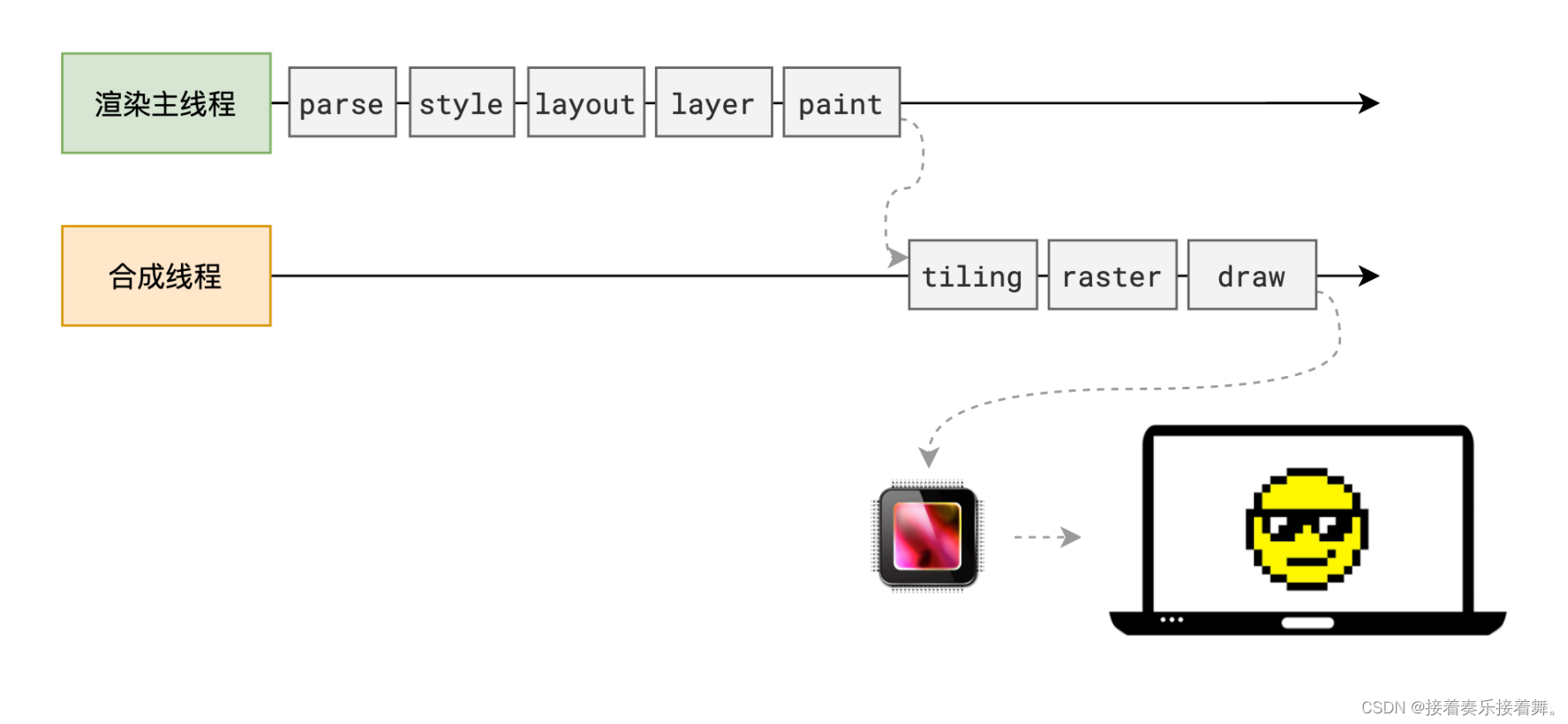
【前端】浏览器的渲染流程(完整)
本文主要包含以下内容:浏览器渲染整体流程解析 HTML样式计算布局分层生成绘制指令分块光栅化绘制常见面试题浏览器渲染整体流程浏览器,作为用户浏览网页最基本的一个入口,我们似乎认为在地址栏输入 URL 后网页自动就出来了。殊不知在用户输入…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
