当前位置： 首页 > news >正文

【25考研】- 整体规划及高数一起步

news 2026/2/10 13:05:43

【25考研】- 整体规划及高数一起步

  • 一、整体规划
  • 二、专业课870计算机应用基础
    • 参考网上考研学长学姐：
  • 三、高数一典型题目、易错点及常用结论
    • （一）典型题目
    • （二）易错点
    • （三）常用结论
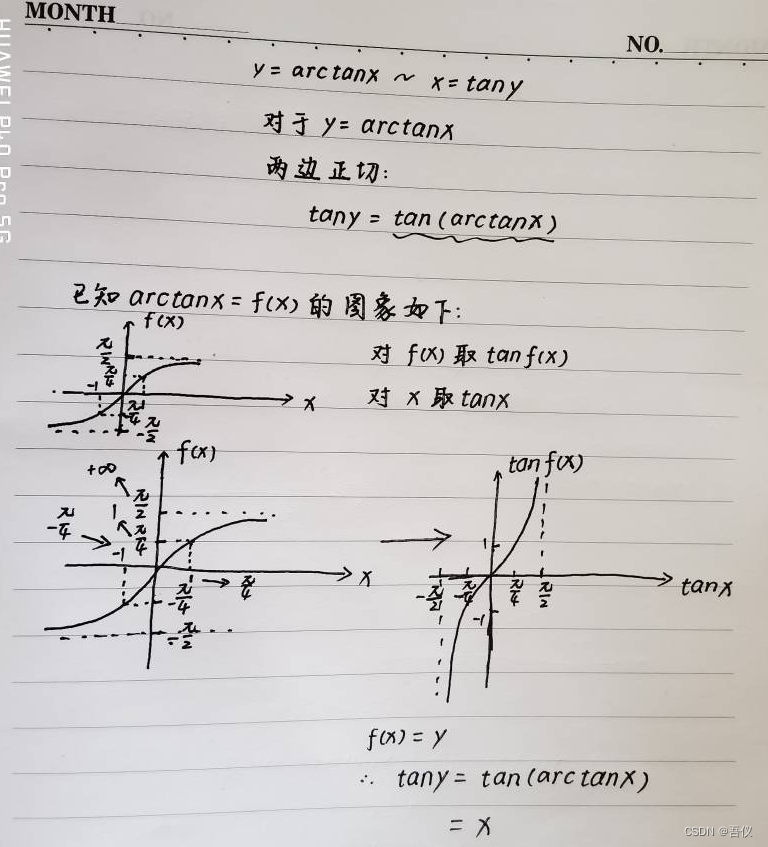
      • 1.令t=arctanx, 则x=tant
      • 2.arcsinx+arccosx=∏/2
      • 3.
      • 4.sec^2 X = tan^2 X + 1
      • 5.洛必达法则

一、整体规划

数（一）150：高数一、线代、概率论
英（一）100
政治 100
870计算机应用基础 150：C语言>数据结构>数据库>计算机基础知识

二、专业课870计算机应用基础

官方给的参考书目是：谭浩强的C程序设计（第五版）和徐士良的计算机软件技术基础（第四版）。计算机软件技术基础这本书包括了数据结构、操作系统、数据库、编译原理、软件工程5门课的内容，但编译原理和软件工程的内容很多年没考过了，可以忽略。

在这里插入图片描述

初试分数构成大概是C语言60％、数据结构30％、操作系统/数据库10％；题型是选择10×3分、读程序写结果6×5分、简答题3×15分、编程题3×15分。

  • 参考网上考研学长学姐：

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

三、高数一典型题目、易错点及常用结论

（一）典型题目

在这里插入图片描述

在这里插入图片描述

（二）易错点

在这里插入图片描述

（三）常用结论

1.令t=arctanx, 则x=tant

在这里插入图片描述

2.arcsinx+arccosx=∏/2

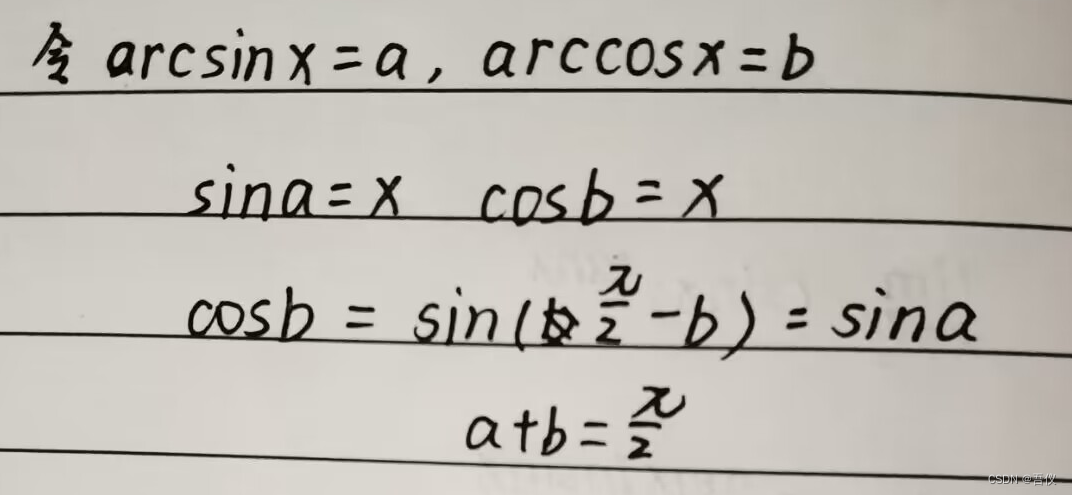
在这里插入图片描述

3.

在这里插入图片描述

4.sec^2 X = tan^2 X + 1

5.洛必达法则

在这里插入图片描述

相关文章：

【25考研】- 整体规划及高数一起步

【25考研】- 整体规划及高数一起步 一、整体规划二、专业课870计算机应用基础参考网上考研学长学姐： 三、高数一典型题目、易错点及常用结论（一）典型题目（二）易错点（三）常用结论1.令tarctanx, 则…...

编程日记 2023/8/30 15:17:52

【Unity】常见的角色移动旋转

在Unity 3D游戏引擎中，可以使用不同的方式对物体进行旋转。以下是几种常见的旋转方式： 欧拉角（Euler Angles）：欧拉角是一种常用的旋转表示方法，通过绕物体的 X、Y 和 Z 轴的旋转角度来描述物体的旋转。在Un…...

编程日记 2023/8/30 15:16:51

今天的小结

1、冒泡排序 冒泡排序（Bubble Sort）是一种简单的排序算法，它重复地遍历待排序的元素列表，比较相邻的元素并交换它们的位置，直到整个列表排序完成。冒泡排序的基本思想是通过不断交换相邻元素，将最大&#…...

编程日记 2023/8/30 15:15:50

了解 Socks 协议：它的过去、现在与未来

在网络世界的江湖中，有一名叫做 Socks 协议的高手，它凭借着一招“代理”绝技，在网络安全领域独步天下。今天，就让我们来了解一下这位神秘高手的过去、现在和未来。 在过去，互联网世界的江湖可谓是风起云涌，…...

编程日记 2023/8/30 15:14:48

小谈静态类和单例模式

静态类（Static Class）和单例（Singleton）都是在编程中用于实现特定类型的设计模式或代码组织方式。它们在不同的情境下有不同的用途和特点。 静态类（Static Class） 静态类是一种类，它的方法和属…...

编程日记 2023/8/30 15:13:47

​LeetCode解法汇总823. 带因子的二叉树

目录链接： 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目： https://github.com/September26/java-algorithms 原题链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台 描述： 给出一个含…...

编程日记 2023/8/30 15:12:46

TypeScript的变量声明的各种方式

TypeScript是一种静态类型的JavaScript超集，它为JavaScript代码提供了类型检查和更好的代码组织结构。在TypeScript中，变量声明是非常重要的，因为它们定义了变量的类型和范围。本文将详细介绍TypeScript的变量声明，并通过代码案例…...

编程日记 2023/8/30 15:11:44

c++ lambda

Lambda Lambda 表达式一般用于定义匿名函数，使得代码更加灵活简洁，优点： 声明式编程风格：就地匿名定义目标函数或函数对象，不需要额外写一个命名函数或者函数对象。以更直接的方式去写程序，好的可读性和可…...

编程日记 2023/8/30 15:10:43

泊松回归和地理加权泊松回归

01 泊松回归 泊松回归（Poisson Regression）是一种广义线性模型，用于建立离散型响应变量（计数数据）与一个或多个预测变量之间的关系。它以法国数学家西蒙丹尼泊松（Simon Denis Poisson）的名字命名，适用于计算“事件发生次数”的概率，比如交通事故发生次数、产品缺陷数…...

编程日记 2023/8/30 15:09:38

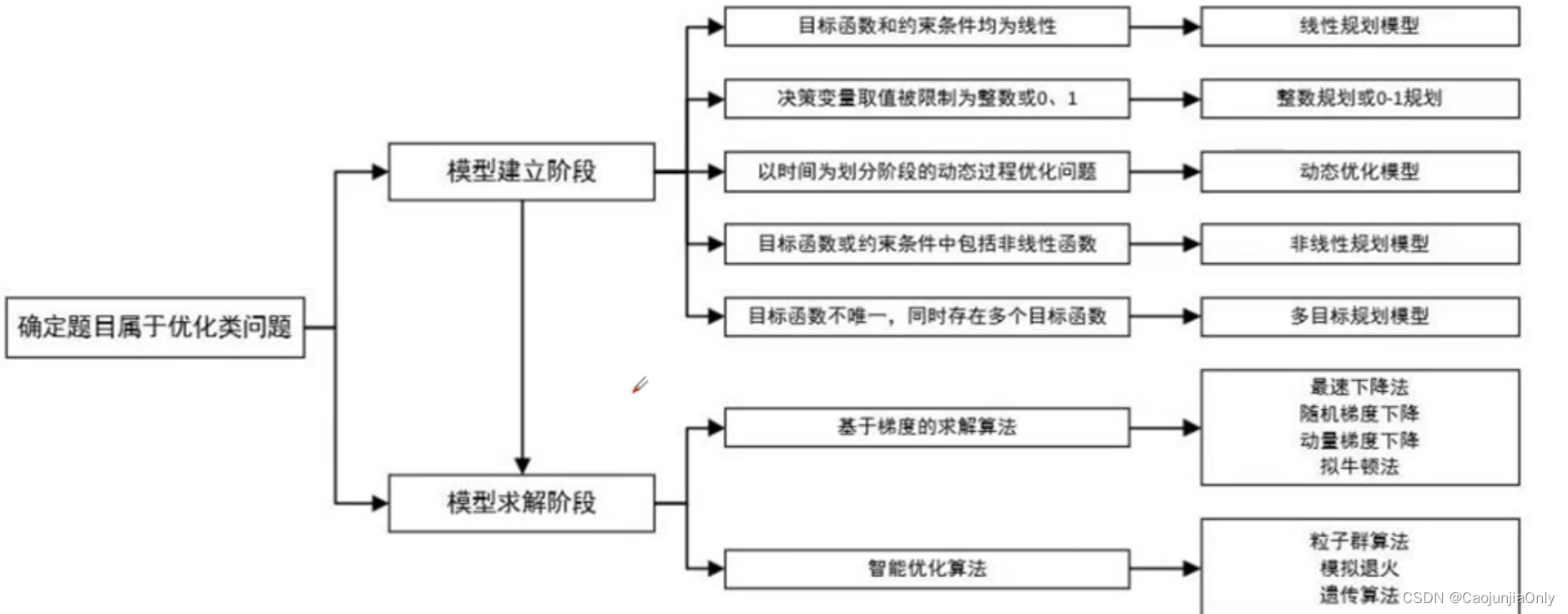
【数学建模竞赛】各类题型及解题方案

评价类赛题建模流程及总结 建模步骤 建立评价指标->评价体系->同向化处理（都越多越好或越少越少）->指标无量纲处理 ->权重-> 主客观->合成 主客观评价问题的区别 主客观概念主要是在指标定权时来划分的。主观评价与客观评价的区别…...

编程日记 2023/8/30 15:08:30

【12期】谈一谈redis两种持久化机制的区别？

Redis两类持续性的方法 RDB方案可以在规定时间间隔内创建数据集的时间点快照。 AOF方案记录了服务器执行的所有写操作命令，并在服务器启动时通过重新执行这些命令来还原数据集。AOF文件完全遵循Redis协议格式保存，新命令会被追加到文件末尾。此外&#…...

编程日记 2023/8/30 15:07:29

Lambda 编程（Kotlin）一

学习记录，以下为个人理解 知识点： Lambda的定义：允许你把代码块当作参数传递给函数Lambda的语法约定：如果lambda 表达式是函数调用的最后一个实参，它可以放到括号的外边当lambda表达式时函数唯一的实参时&#xff0c…...

编程日记 2023/8/30 15:06:26

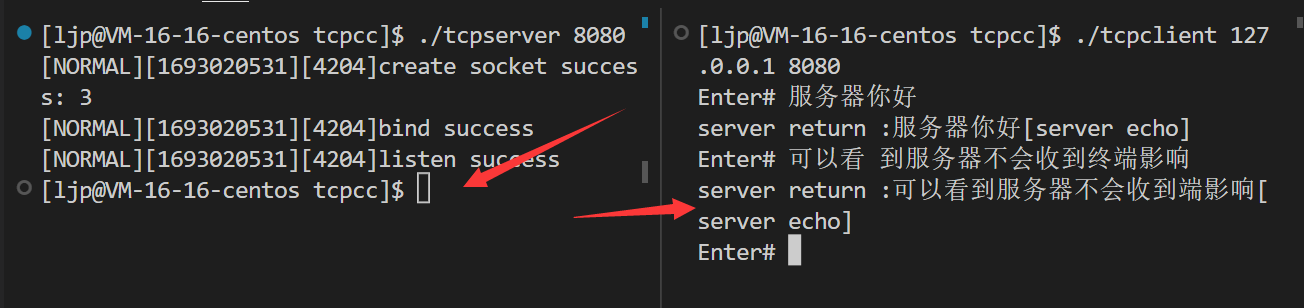
网络字节序——TCP接口及其实现简单TCP服务器

网络字节序——TCP接口及其实现简单TCP服务器 文章目录 网络字节序——TCP接口及其实现简单TCP服务器简单TCP服务器的实现1. 单进程版：客户端串行版2. 多进程版：客户端并行版netstat查看网络信息3.多线程版：并行执行log.hpp 守护进程fg、bg s…...

编程日记 2023/8/30 15:05:25

RxJS如何根据事件创建Observable对象？

RxJS提供了一些用来创建Observable对象的函数，我们可以根据事件、定时器、Promise，AJAX等来创建Observable对象。 下面是根据事件创建Observable对象的几个例子。 this.outsideClick$ fromEvent(document, click).subscribe((event: MouseEvent) > …...

编程日记 2023/8/30 15:04:25

网站常见安全漏洞 | 青训营

Powered by:NEFU AB-IN 文章目录 网站常见安全漏洞 | 青训营 网站基本组成及漏洞定义服务端漏洞SQL注入命令执行越权漏洞SSRF文件上传漏洞 客户端漏洞开放重定向XSSCSRF点击劫持CORS跨域配置错误WebSocket 网站常见安全漏洞 | 青训营 网站常见安全漏洞-网站基本组成及漏洞定义…...

编程日记 2023/8/30 15:03:24

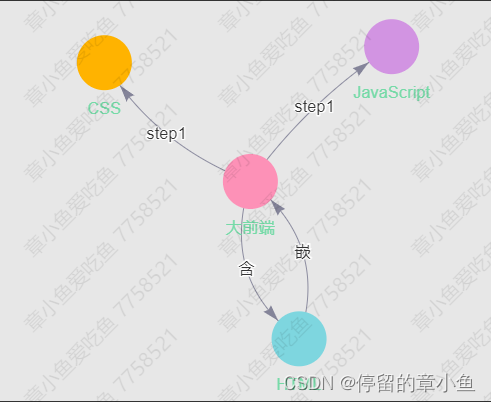
vue2使用 vis-network 和 vue-vis-network 插件封装一个公用的关联关系图

效果图&#xff1a; vis组件库&#xff1a;vis.js vis-network中文文档&#xff1a;vis-network 安装组件库&#xff1a; npm install vis-network vue-vis-network 或 yarn add vis-network vue-vis-network 新建RelationGraph.vue文件&#xff1a; <template><…...

编程日记 2023/8/30 15:02:22

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。

LeetCode第73题矩阵置零 1.思路&#xff1a; 想到一个开辟一点空间来解决方法&#xff0c;使用哈希集。就是使用一个哈希集&#xff08;row和col&#xff09;来储存数组中的元素为0的下标。然后再遍历&#xff0c;整个二维数组&#xff0c;在哈希集中存在对应的下标&#xff0c…...

编程日记 2023/8/30 15:01:21

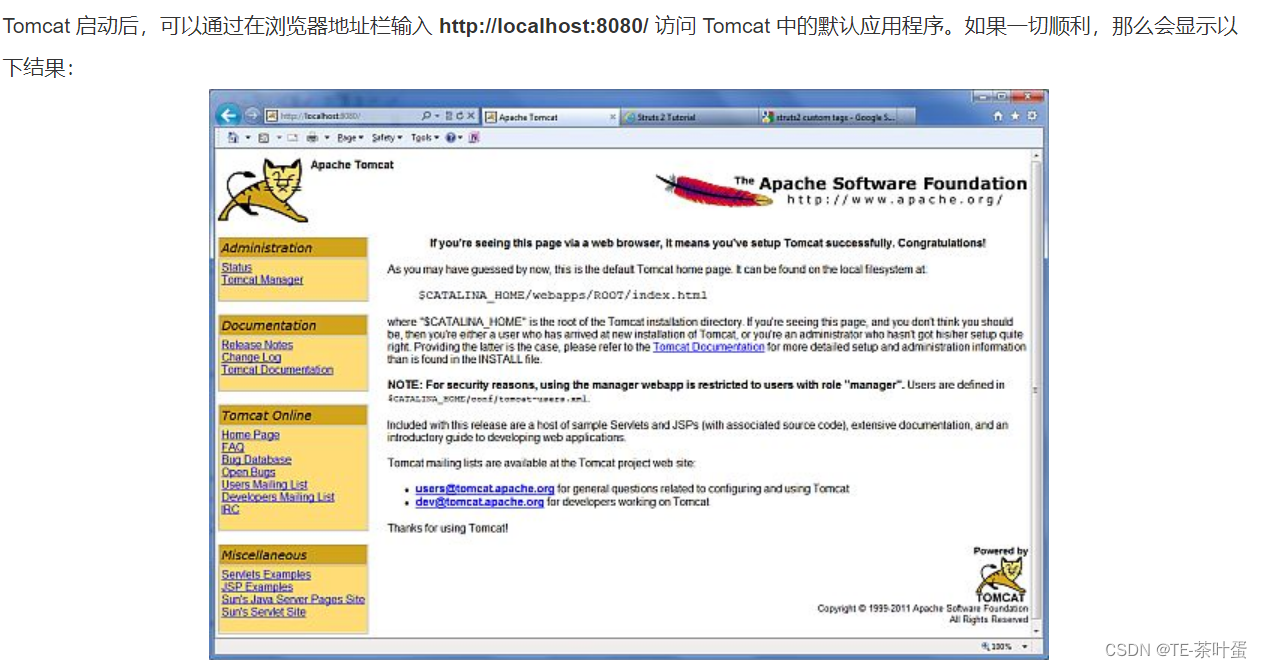
java-初识Servlet,Tomcat，JDBC

文章目录 前言一、ServletServlet 生命周期Servlet 实例Servlet 过滤器 二、TomcatJDBCJDBC连接数据库实例 总结 前言 java入门须知的重要概念/名词/技术 等 一、Servlet Servlet是Java Web开发中的一个核心组件&#xff0c;它是基于Java语言编写的服务器端程序&#xff0c;…...

编程日记 2023/8/30 15:00:19

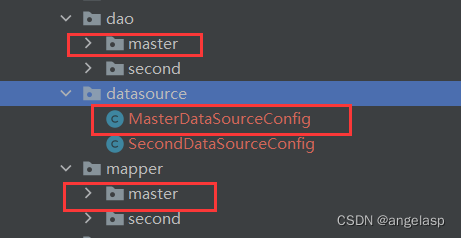
SpringBoot+mybatis+pgsql多个数据源配置

一、配置文件 jdk环境&#xff1a;1.8 配置了双数据源springbootdruidpgsql&#xff0c;application.properties配置修改如下&#xff1a; #当前入库主数据库 spring.primary.datasource.typecom.alibaba.druid.pool.DruidDataSource spring.primary.datasource.driver-class…...

编程日记 2023/8/30 14:59:17

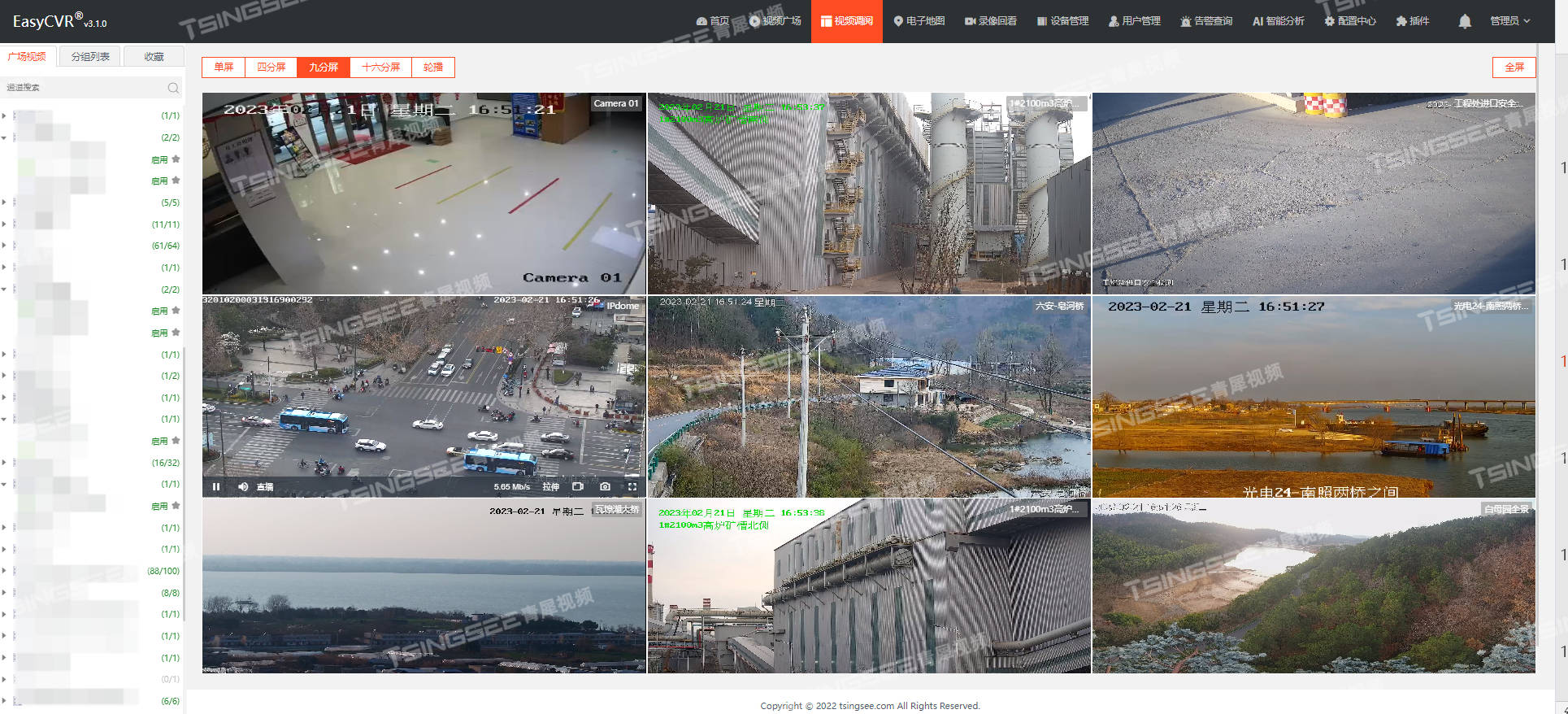
视频汇聚/视频监控管理平台EasyCVR接入海康SDK协议后无法播放该如何解决？

开源EasyDarwin视频监控/安防监控/视频汇聚EasyCVR能在复杂的网络环境中&#xff0c;将分散的各类视频资源进行统一汇聚、整合、集中管理&#xff0c;在视频监控播放上&#xff0c;视频安防监控汇聚平台可支持1、4、9、16个画面窗口播放&#xff0c;可同时播放多路视频流&#…...

编程日记 2023/8/30 14:58:16

Vim 调用外部命令学习笔记

Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

编程新知 2025/11/16 8:24:16

Spark 之 入门讲解详细版（1）

1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室&#xff08;Algorithms, Machines, and People Lab&#xff09;开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目&#xff0c;8个月后成为Apache顶级项目&#xff0c;速度之快足见过人之处&…...

编程新知 2026/2/5 4:17:31

k8s从入门到放弃之Ingress七层负载

k8s从入门到放弃之Ingress七层负载 在Kubernetes&#xff08;简称K8s&#xff09;中&#xff0c;Ingress是一个API对象&#xff0c;它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress&#xff0c;你可…...

编程新知 2025/9/7 0:12:53

Docker 运行 Kafka 带 SASL 认证教程

Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明&#xff1a;server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

编程新知 2026/1/23 4:15:03

蓝桥杯 2024 15届国赛 A组 儿童节快乐

P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡&#xff0c;轻快的音乐在耳边持续回荡&#xff0c;小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下&#xff0c;六一来了。 今天是六一儿童节&#xff0c;小蓝老师为了让大家在节…...

编程新知 2025/12/5 2:40:04

学校招生小程序源码介绍

基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码&#xff0c;专为学校招生场景量身打造&#xff0c;功能实用且操作便捷。 从技术架构来看&#xff0c;ThinkPHP提供稳定可靠的后台服务&#xff0c;FastAdmin加速开发流程&#xff0c;UniApp则保障小程序在多端有良好的兼…...

编程新知 2026/1/26 14:19:52

力扣-35.搜索插入位置

题目描述 给定一个排序数组和一个目标值&#xff0c;在数组中找到目标值&#xff0c;并返回其索引。如果目标值不存在于数组中&#xff0c;返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

编程新知 2025/12/3 3:22:43

重启Eureka集群中的节点，对已经注册的服务有什么影响

先看答案&#xff0c;如果正确地操作&#xff0c;重启Eureka集群中的节点&#xff0c;对已经注册的服务影响非常小&#xff0c;甚至可以做到无感知。 但如果操作不当&#xff0c;可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

编程新知 2025/9/24 3:38:34

vulnyx Blogger writeup

信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面&#xff0c;gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress&#xff0c;说明目标所使用的cms是wordpress&#xff0c;访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

编程新知 2026/1/29 5:24:50

4. TypeScript 类型推断与类型组合

一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式&#xff0c;自动确定它们的类型。 这一特性减少了显式类型注解的需要&#xff0c;在保持类型安全的同时简化了代码。通过分析上下文和初始值&#xff0c;TypeSc…...

编程新知 2025/11/2 1:48:43