HOT100打卡—day10—【DP+多维DP】—最新8.29(剩6题)
DP
1 70. 爬楼梯
70. 爬楼梯
一次做,AC代码:
疑问:怎么判断用搜索还是dp?这题,我没有受过dp训练所以第一反应是用dfs搜索,找到所有符合要求的叶子。
class Solution {
public:int dp[50]; // step1:含义: 对于下标i 有多少种方案到第i层/*step2:状态转移方程 dp[i] = dp[i-2] + dp[i-1]step3: dp数组初始化 dp[1] = 1 , dp[2] = 2step4: 遍历顺序 i递增step5: 模拟 1,2,3(1 1 1 + 2 1 +1 2 ),5*/ int climbStairs(int n) {// 这题我的第一感觉是搜索 什么时候用dp????dp[1] = 1;dp[2] = 2;for(int i = 3; i <= n; i++)dp[i] = dp[i-1] + dp[i-2];return dp[n];}
};2 118. 杨辉三角
118. 杨辉三角
简单,AC:
class Solution {
public:vector<vector<int>> ans;vector<vector<int>> generate(int numRows) {vector<int> tmp;tmp.push_back(1);ans.push_back(tmp);if(numRows == 1)return ans;tmp.clear();tmp.push_back(1);tmp.push_back(1);ans.push_back(tmp);if(numRows == 2)return ans;for(int i = 3; i <= numRows;i++){tmp.clear();tmp.push_back(1);for(int j = 0; j < ans[ans.size()-1].size()-1;j++){tmp.push_back(ans[ans.size()-1][j] + ans[ans.size()-1][j + 1]);}tmp.push_back(1);ans.push_back(tmp);}return ans;}
};3 198. 打家劫舍
198. 打家劫舍
就按照五部曲思考,AC代码:
class Solution {
public:int dp[120]; // 从左往右偷 偷到第i个房子(不包含本房子)时候已经赚了的最多钱/*dp[i] = max(dp[i-1] + 0,dp[i-2]+nunms[i-2])dp[0] = 0dp[1] = 0升序模拟 样例2=== 0 0 2 7 11*/int rob(vector<int>& nums) {dp[0] = 0;dp[1] = 0;if(nums.size() == 1)return nums[0];int i = 2;for(; i < nums.size();i++)dp[i] = max(dp[i-1] + 0,dp[i-2]+nums[i-2]);return max(dp[i-1] + nums[i - 1],dp[i-2]+nums[i-2]); // 这里的return 和状态转移方程不太一样}
};4 279. 完全平方数
279. 完全平方数
之前没学多重背包之前看到题目是蒙的,现在学完完全背包很自然就做出来了,AC代码:
class Solution {
public:int dp[10010]; // dp[1]表示 凑成i的完全平方数最少需要的数目/*转成完全背包物品:i = 1....sqrt(n)背包:ndp[j] = min(dp[j- i]+1,dp[j])装i 不撞idp[0] = 0 其他非0下标全设为INT_MAXi++j++模拟——*/int numSquares(int n) {dp[0] = 0;for(int j = 1; j <= n; j++)dp[j] = INT_MAX;for(int i = 1; i*i <= n; i++){for(int j = 0; j <= n; j++){if(j >= i*i)dp[j] = min(dp[j- i*i]+1,dp[j]);else dp[j] = dp[j];}// for(int j = 0; j <= n; j++) cout << dp[j] << ' ';// puts("");}return dp[n];}
};5 518. 零钱兑换 II + 322. 零钱兑换
518. 零钱兑换 II
根据上面学的理论,一次AC代码:
class Solution {
public:int dp[5005]; // 能正好装满i的背包的方式数目/*dp[j] += dp[j - coins[i]];dp[0] = 1;i++ j++模拟——*/int change(int amount, vector<int>& coins) {dp[0] = 1;for(int i = 0; i < coins.size(); i++)for(int j = 0; j <= amount; j++)if(j >= coins[i])dp[j] += dp[j - coins[i]];return dp[amount];}
};322. 零钱兑换
类似的一题:
class Solution {
public:long long dp[10005]; // 能正好装满i的背包的最少硬币个数/*dp[j] = min(dp[j],dp[j - coins[i]] + 1)不装i 装idp[0] = 0;其他非0下标初始化为INT_MAXi++ j++模拟——0 1 2 3 4 5 6 7 8 9 10 11 0 1 1 2 2 3 3 4 4 5 5 6 0 1 1 2 2 1 2 2 3 3 2 3 */int coinChange(vector<int>& coins, int amount) {dp[0] = 0;for(int i = 1; i <= amount; i++)dp[i] = INT_MAX;for(int i = 0; i < coins.size(); i++){for(int j = 0; j <= amount; j++)if(j >= coins[i])dp[j] = min(dp[j],dp[j - coins[i]] + 1);// for(int j = 0; j <= amount; j++)cout << dp[j] << ' ';// cout << endl;}if(dp[amount] == INT_MAX)return -1;else return dp[amount];}
};6 139. 单词拆分
139. 单词拆分
做了很久...估计2h 一开始我的思路卡死了 + 看题解之后的思路的详解见注释,
我的写法和carl 答案在一些微小的细节上略有不同,我的更好理解,但他的解法更简单。
我写的过程中,需要注意下标和字符串大小的关系要不要+1-1,而且dp[] 需要从1开始到n有意义,dp[0] 不管它。不可以只有0,...,n-1 这样会忽略s = "a" Dict = ["b"] 这样的样例,因为dp[0] 恒为1。
AC代码:
class Solution {
public://多重背包且排列/*一开始我的思路——物品:字典里面str背包:容量为?的背包 求装满时候的情况dp[wordDict.size()][s.size()]如果n = wordDict.size() m = s.size() 又感觉要考虑每个字符和Dict中每个字符串的关系 很麻烦 *//*看了题解,才知道我纠结的地方 每个字符和Dict中每个字符串的关系 很麻烦,但其实可以用substr函数考虑背包的s的子串和Dict中每个字符串来比较,这样就变得很简单了。而且之前思考时候不知道dp[]存的值要是int还是char什么东西其实就题目结果反推,dp[] = trur/flase*/bool dp[310]; //以i结尾的字符串是否可以利用字典中出现的单词拼接出来/*dp[j] = dp[j - wordDict[i].size()] && substr(s,j - wordDict[i].size(),wordDict[i].size()) == wordDict[i];dp[0] = 1;多重背包+排列背包j++ 物体i++模拟——6 7 8 9 10 11j = 11 size = 5 dp[6]*/bool wordBreak(string s, vector<string>& wordDict) {dp[0] = 1;bool tmp[100][100];for(int j = 0; j <= s.size();j++){for(int i = 0; i < wordDict.size();i++){if(j == wordDict[i].size()) // 能装下一个dp[j] = (s.substr(j - wordDict[i].size(),wordDict[i].size()) == wordDict[i]) || dp[j];else if(j > wordDict[i].size() ) // 能至少装2个 dp[j] = dp[j - wordDict[i].size()] && (s.substr(j - wordDict[i].size(),wordDict[i].size()) == wordDict[i]) || dp[j];}}// for(int i = 0; i < wordDict.size();i++)// {// for(int j = 0; j < s.size();j++)// cout << tmp[i][j] << ' ';// cout << endl;// }return dp[s.size() ];}
};7
8
9 01背包应用题——416. 分割等和子集
416. 分割等和子集
一开始看到题目,想用贪心——排序+双指针 每次都把当前相对小的放进小的sum中,写完之后发现过不了:[1,1,2,2]这样的样例。错误代码:
class Solution {
public:/*左边的sum 小于 右边的sum l++,左边的sum+=左边的sum 大于 同理如果等于左边前进 1,2,3,4, 5,6,7,8,9, 10*/bool canPartition(vector<int>& nums) {// 解法1:排序+双指针if(nums.size() == 1)return 0;sort(nums.begin(),nums.end());int l = 0;int r = nums.size() - 1;int leftsum = 0;int rightsum = 0;while(l <= r){if(leftsum <= rightsum){leftsum += nums[l++];}else{rightsum += nums[r--];}}cout << l << " " << r << endl;cout << leftsum << " " << rightsum;if(leftsum == rightsum)return 1;else return 0;}
};要明确本题中我们要使用的是01背包,因为元素我们只能用一次。
回归主题:首先,本题要求集合里能否出现总和为 sum / 2 的子集。
那么来一一对应一下本题,看看背包问题如何来解决。
只有确定了如下四点,才能把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
具体分析过程见注释, AC代码:
class Solution {
public:// 找到一个背包 能够装nums.total(所有物体重量总和)/2的东西int dp[10005]; // 容积为i的背包 根据现有的物体重量情况最多能装的物体的重量/*转换成01背包问题:假设有一个nums.total/2的背包有若干个物体,每个物体的重量就是nums[i] 本题可以舍弃价值这个概念就是问一个nums.total/2的背包最多能够装的物体的重量是多少 能不能达到nums.total/2if(j < nums[i])dp[j] = dp[j];else dp[j] = max(dp[j] , dp[j - nums[i]]+nums[i]);dp[0] = 0;其他默认是0for物体i++ for容积j--模拟——*/bool canPartition(vector<int>& nums) {dp[0] = 0;int total = 0;for(auto i : nums)total += i;if(total % 2 == 0)total /= 2;else return 0;for(int i = 0; i < nums.size();i++){for(int j = total ; j >= 0; j--){if(j < nums[i])dp[j] = dp[j];else dp[j] = max(dp[j] , dp[j - nums[i]]+nums[i]);}}if(dp[total] == total)return 1;else return 0;}
};10
多维DP
1 62. 不同路径
62. 不同路径
自己试着写写,二维dp数组,还是五步曲,AC代码:
class Solution {
public:int dp[105][105];// (i,j) 表示到达这个格子最多几条不同的路径/*状态转移:dp[i][j] = dp[i-1][j] + dp[i][j-1];dp数组初始化(初始化 第一行和第一列)dp[0][0] = 0dp[0][x] = 1dp[x][0] = 1顺序:for(i++)中for(j++)模拟一下2*30 1 11 2 3*/int uniquePaths(int m, int n) {// 原来 用dp 不用搜索 是因为怕超时dp[0][0] = 0;for(int i = 1; i < n; i++)dp[0][i] = 1;for(int i = 1; i < m; i++)dp[i][0] = 1;for(int i = 1; i < m;i++)for(int j = 1; j < n; j++)dp[i][j] = dp[i-1][j] + dp[i][j-1];if(m == 1 && n == 1)return 1; // 特殊处理return dp[m-1][n-1];}
};1.2 63. 不同路径 II(有障碍物版本的上一题)
63. 不同路径 II
有障碍物就是加一堆if-else ,自己写的 ,然后debug半天很多边界通过反复提交才试出来,比如:
if(m == 1 && n == 1)return obstacleGrid[0][0] ^ 1; // 因为dp[0]设置为0 所以要特殊处理
if(obstacleGrid[0][0] || obstacleGrid[n-1][m-1] || dp[n-1][m-1] == -1)return 0; //特殊处理起点有障碍物 、终点有障碍物、 终点不可达(三种情况)
AC代码:
class Solution {
public:int dp[105][105];// (i,j) 表示到达这个格子最多几条不同的路径 -1表示不可达/*状态转移:if(obs[i-1][j] == 0 && dp[i-1][j] != -1) // 上一个不是障碍物且可达dp[i][j] += dp[i-1][j]if(obs[i][j-1] == 0 && dp[i][j-1] != -1) // 左边一个不是障碍物且可达dp[i][j] += dp[i][j-1]if((obs[i-1][j] == 1 || dp[i-1][j] == -1) && (obs[i][j-1] == 1 || dp[i][j-1] == -1))if(obstacleGrid[i][j]) // 两个都不能达到我 或者我本身是障碍物dp[i][j] = -1dp数组初始化(初始化 第一行和第一列)dp[0][0] = 0dp[0][x] = 1 这一行第一个障碍物 后面的格子都不可达 设为-1dp[x][0] = 1 这一列第一个障碍物 下面的格子都不可达 设为-1顺序:for(i++)中for(j++)模拟一下3*30 1 11 -1 11 1 1*/int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {dp[0][0] = 0;int n = obstacleGrid.size(); // 行int m = obstacleGrid[0].size();int x = 1;for(int i = 1; i < n; i++){if(obstacleGrid[i][0] == 1)x = -1;dp[i][0] = x;}x = 1;for(int i = 1; i < m; i++){if(obstacleGrid[0][i] == 1)x = -1;dp[0][i] = x;}for(int i = 1; i < n;i++)for(int j = 1; j < m; j++){if(obstacleGrid[i-1][j] == 0 && dp[i-1][j] != -1)dp[i][j] += dp[i-1][j];if(obstacleGrid[i][j-1] == 0 && dp[i][j-1] != -1)dp[i][j] += dp[i][j-1];if((obstacleGrid[i-1][j] == 1 || dp[i-1][j] == -1) && (obstacleGrid[i][j-1] == 1 || dp[i][j-1] == -1)) // 两个都满dp[i][j] = -1;if(obstacleGrid[i][j])dp[i][j] = -1;}for(int i = 0; i < n; i++){for(int j = 0; j < m; j++)cout << dp[i][j] << " ";cout << endl;}if(m == 1 && n == 1)return obstacleGrid[0][0] ^ 1; // 因为dp[0]设置为0 所以要特殊处理if(obstacleGrid[0][0] || obstacleGrid[n-1][m-1] || dp[n-1][m-1] == -1)return 0; //特殊处理起点有障碍物 、终点有障碍物、 终点不可达return dp[n-1][m-1];}
};看了题解,思路差不多,就是它遇到障碍dp[i][j]保持0,然后状态转移方程就可以写的很简单。
直接复制粘贴的代码:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍,直接返回0return 0;vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};2 64. 最小路径和
64. 最小路径和
和62.不同路径差不多。
AC代码:
class Solution {
public:int dp[210][210]; // (i,j)表示从起点出发到(i,j)的路径数字总和最小的数/*dp[i][j] = min(d[i-1][j]+grid[i][j] , d[i][j-1]+grid[i][j])dp[0][0] = grid[0][0]dp[0][j] += grid[0][j]dp[i][0] += grid[i][0]i++j++*/int minPathSum(vector<vector<int>>& grid) {int n = grid.size();int m = grid[0].size();dp[0][0] = grid[0][0];for(int j = 1; j < m; j++)dp[0][j] = dp[0][j-1]+grid[0][j];for(int i = 1;i < n; i++)dp[i][0] = dp[i-1][0]+grid[i][0];for(int i = 1; i < n; i++)for(int j = 1; j < m; j++ )dp[i][j] = min(dp[i-1][j]+grid[i][j] , dp[i][j-1]+grid[i][j]);return dp[n-1][m-1];}
};3
4
5
相关文章:
)
HOT100打卡—day10—【DP+多维DP】—最新8.29(剩6题)
DP 1 70. 爬楼梯 70. 爬楼梯 一次做,AC代码: 疑问:怎么判断用搜索还是dp?这题,我没有受过dp训练所以第一反应是用dfs搜索,找到所有符合要求的叶子。 class Solution { public:int dp[50]; // step1&a…...
【不会用这个工具,你的Linux服务器就是个摆设!】
01 Tcpdump Tcpdump 是一个强大的网络监控工具,它允许用户有效地过滤网络上的数据包和流量。 这可以获得有关 TCP/IP 和网络上传输的数据包的详细信息。 当你遇到网络协议问题一筹莫展的时候,这时候往往可以通过tcpdump来看网络的通讯过程中发生了什么…...

09 生产者分区机制
kafka如何保证消息的有序 可以通过key-ording策略解决。kafka可以为每条消息定义消息键,也称为key,通常是带有业务属性的比如用户id之类的。有相同消息键的消息会被发到同一个分区。下面实现了key-ordering策略,对key的hashcode进行取模来决…...
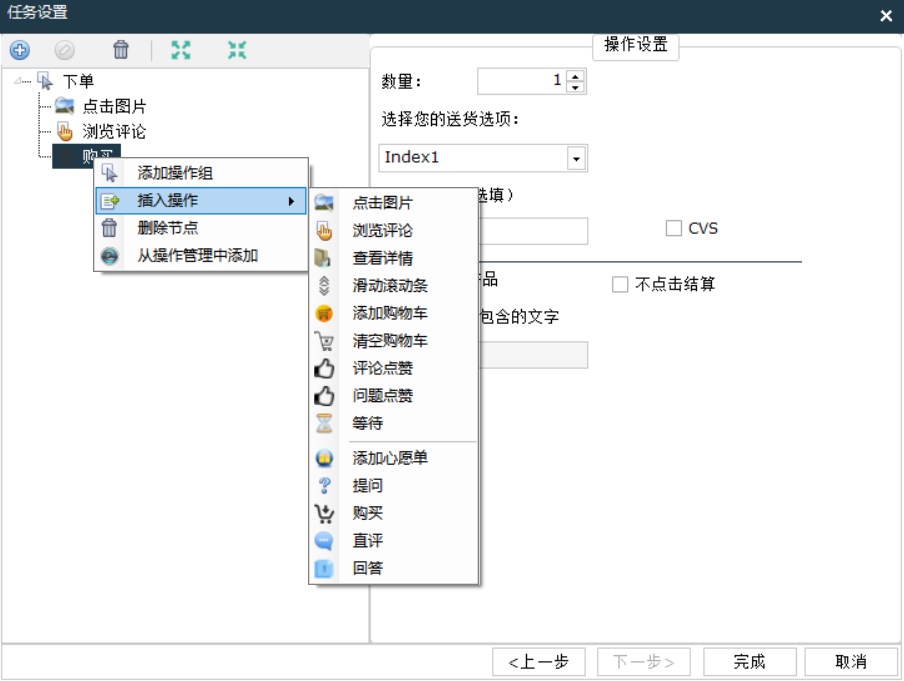
亚马逊鲲鹏系统是怎么操作测评的
亚马逊鲲鹏系统可以注册亚马逊买家号、养号、下单留评等,是一款功能比较齐全的测评软件,具体操作如下: 首先我们需要先准备好买家账号,账号可以直接去购买已经注册好了的账号,也可以准备好账号所需要的一些邮箱、ip、…...

电脑上的视频如何导入苹果手机?
AirDroid支持Windows、macOS、android、iOS相互传输文件、视频、图片等。 想要从电脑传输文件到iPhone也很简单,在电脑和iPhone都安装AirDroid,连接同一网络,然后登录同一个帐号就可以了。可绑定的iPhone数量不限,只要都登录同一…...
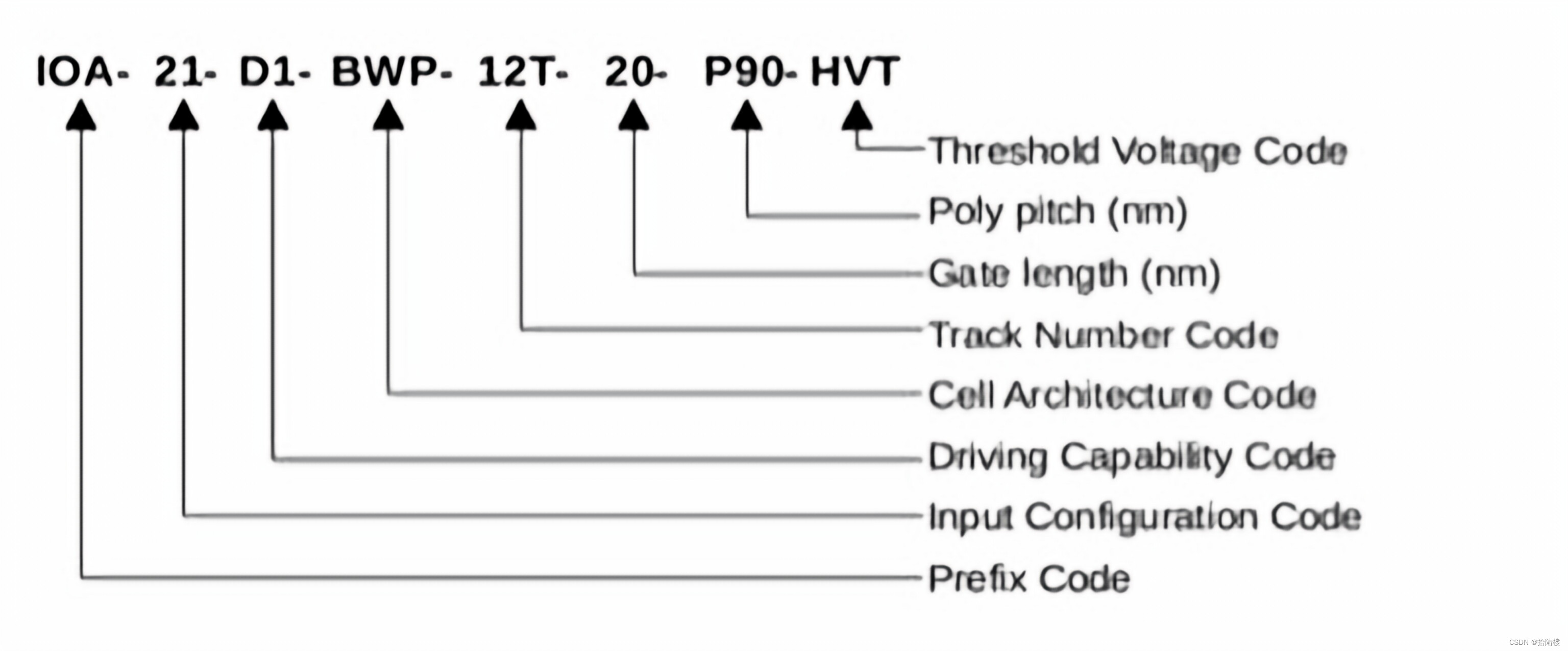
tsmc standard cell命名规则
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧? 拾陆楼知识星球入口 CKMUX2代表二输入clock mux,D2代表驱动强度X2,6T代表row高为6track,16P96C代表gate length和poly pitch,LVT就是low voltage thr…...

基于ssm医院在线挂号预约系统源码和论文
基于ssm医院在线挂号预约系统源码和论文072 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 课题研究的目的及意义: 专家号难求,是医院现场挂号存在的主要问题之一,每一名专…...

mysql binlog 浅谈
如何开启MySQL的binlog日志 在MySQL中,binlog指的是binary log,二进制日志文件。这个文件记录了MySQL所有的DML操作。通过binlog日志,我们可以做数据恢复,做主从复制等等。对于运维或架构人员来说,开启binlog日志功能…...

three.js(八):内置的三维几何体
三维几何体 BoxGeometry 立方体TetrahedronGeometry 四面体OctahedronGeometry 八面体DodecahedronGeometry 十二面体IcosahedronGeometry 二十面体PolyhedronGeometry 多面体SphereGeometry 球体ConeGeometry 圆锥CylinderGeometry 圆柱TorusGeometry 三维圆环TorusKnotGeomet…...
IDEA 性能优化
前言 IDEA 基于JVM,是内存紧张型的应用,即使是16GB内存也很一般。 机器配置: win10 proi7-4720hq 3.2G 4c8tddr3-1600IDEA 2023.2.1 本文优化在不升级硬件的前提下使用 优化 调整JVM堆内存及GC IDEA 自身的JVM运行时配置,启动…...

react 获取表单中输入框的值
通过使用useState钩子来创建一个状态变量,你可以同时获取多个Input框的值。 1获取input框的值: import React, { useState } from react;function MyComponent() {const [forms, setForms] useState({name: ,nation: ,});const handleInputChange (e…...
[虚幻引擎 UE5] EditableText(可编辑文本) 限制只能输入数字并且设置最小值和最大值
本蓝图函数可以格式化 EditableText 控件输入的数据,让其只能输入一定范围内的整数。 蓝图函数 调用方法 下载蓝图(5.2.1版本)https://dt.cq.cn/archives/618...

Docker技术--Docker容器管理
1.Docker容器相关的指令(单个容器操) 我们之前在Docker中部署了一个实际应用的案例wordpress,其中使用到了一些相关于容器的指令,那么下面我们一起来总结使用。 Docker指令的语法规则如下所示: Docker + 命令关键字 [+参数选项] -1类:关闭、开启、重启、开启自启 systemct…...
three.js(七):内置的二维几何体
二维几何体 PlaneGeometry 矩形平面CircleGeometry 圆形平面RingGeometry 圆环平面 PlaneGeometry 矩形平面 PlaneGeometry(width : Float, height : Float, widthSegments : Integer, heightSegments : Integer) width — 平面沿着X轴的宽度。默认值是1。height — 平面沿着Y…...

golang-bufio 缓冲读
缓冲 IO 计算机中我们常听到这样的两种程序优化方式: 以时间换空间以空间换时间 今天要来看的缓冲IO就是典型的以空间换时间,它的基本原理见上图。简单的解释就是:程序不再直接去读取底层的数据源,而是通过一个缓冲区来进行读取…...

前端 js实现 选中数据 动态 添加在表格中
如下图展示,表格上方有属性内容,下拉选中后,根据选中的内容,添加在下方的表格中。 实现方式,(要和后端约定,因为这些动态添加的字段都是后端返回的,后端自己会做处理,…...

MySQL—MySQL主从如何保证强一致性
一、前言 涉及到的东西:两阶段提交,binlog三种格式 1、两阶段提交 在持久化 redo log 和 binlog 这两份日志的时候,如果出现半成功的状态,就会造成主从环境的数据不一致性。这是因为 redo log 影响主库的数据,binlog…...
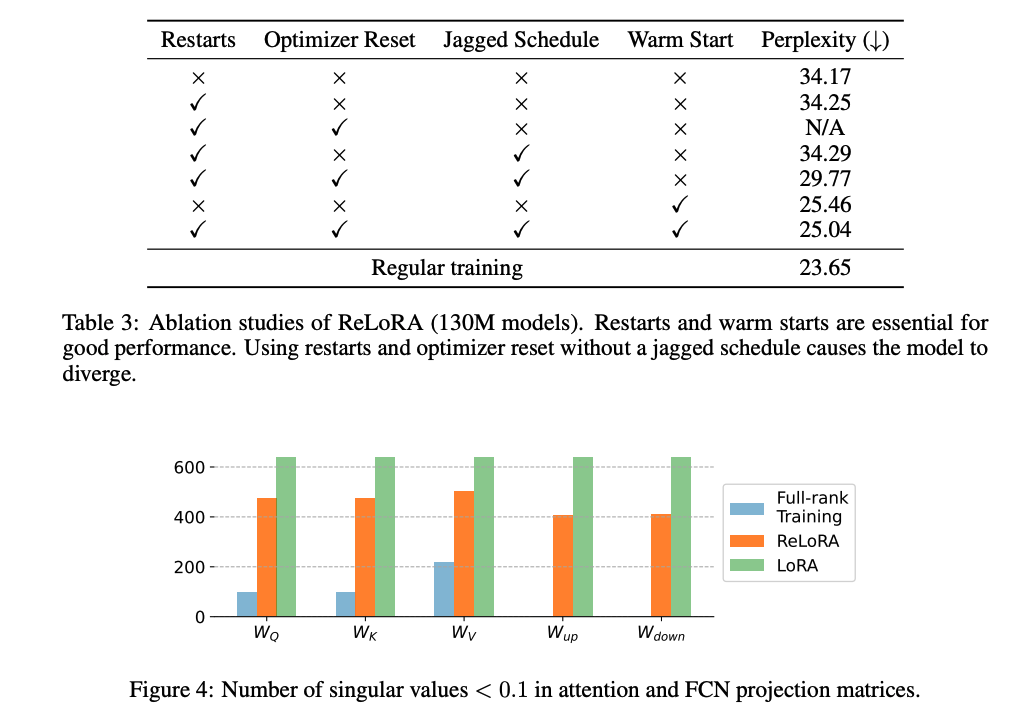
Lora升级!ReLoRa!最新论文 High-Rank Training Through Low-Rank Updates
目录 摘要1 引言2 相关工作3 方法4 实验5 结果6 结论7 局限性和未来工作 关注公众号TechLead,分享AI与云服务技术的全维度知识。作者拥有10年互联网服务架构、AI产品研发经验、团队管理经验,同济本复旦硕,复旦机器人智能实验室成员࿰…...

gateway动态路由和普通路由+负载均衡,借助eureka
gateway 中的动态路由和普通路由是相互独立配置的注意consumer使用了openFeign远程调用的配置文件中 prefer-ip-address: false 必须为false 否则 gateway的动态路由和负载均衡无法实现 spring:cloud:gateway:enabled: truediscovery:locator:enabled: true #表示动态路由&a…...
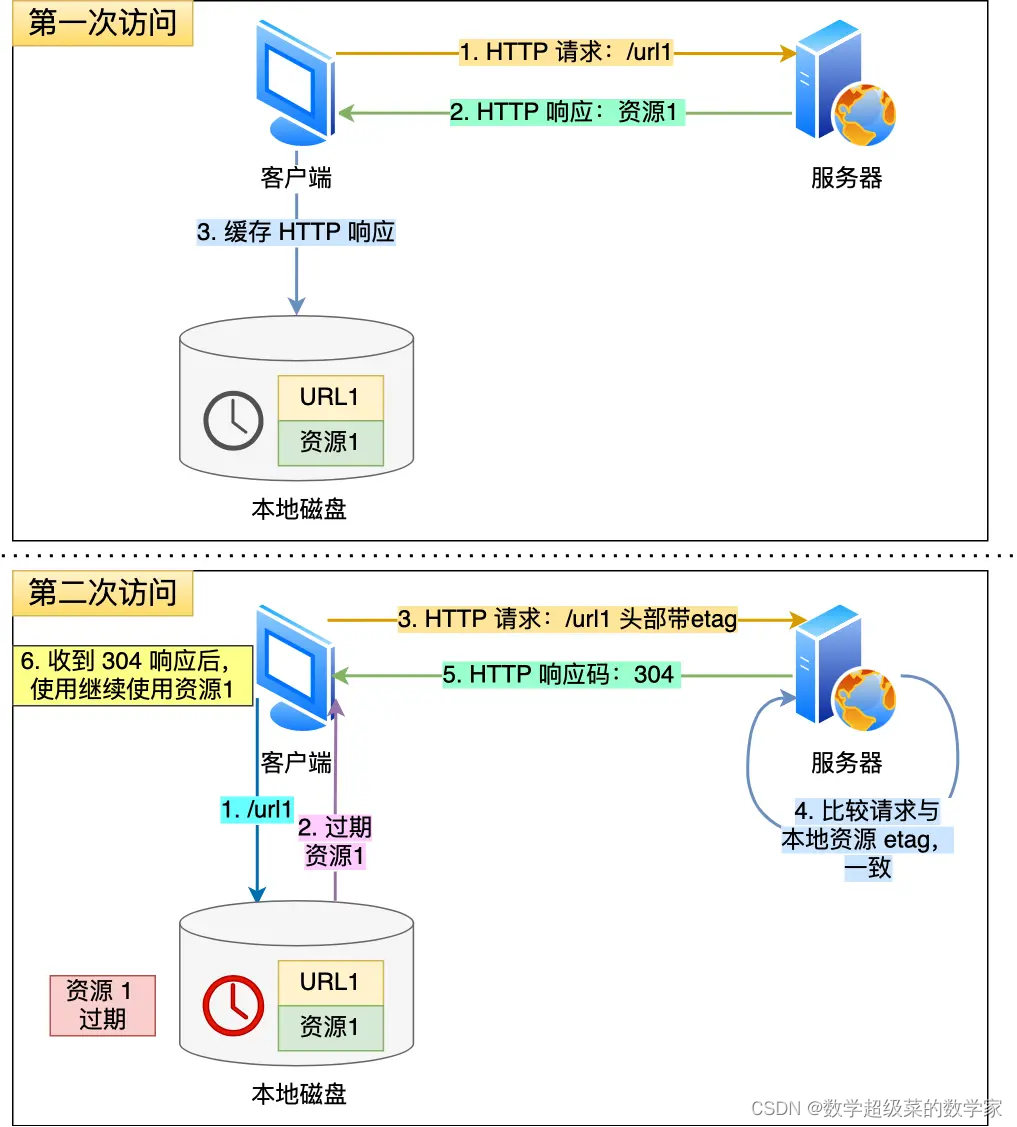
HTTP原理与实现
一、基本概念 一、基本原理* 1、全称: HyperText Transfer Protocol (超文本传输协议) 2、底层实现协议:建立在 TCP/IP 上的无状态连接。 3、基本作用:用于客户端与服务器之间的通信,规定客户端和服务器之间的通信格式。包括请…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
