C语言练习题解析:挑战与突破,开启编程新篇章!(2)
- 💓博客主页:江池俊的博客
- ⏩收录专栏:C语言刷题专栏
- 👉专栏推荐:✅C语言初阶之路 ✅C语言进阶之路
- 💻代码仓库:江池俊的代码仓库
- 🎉欢迎大家点赞👍评论📝收藏⭐

文章目录
- 🌴选择题
- 🌴编程题
- 📌尼科彻斯定理
- 📌等差数列
🎈前言:
- 本专栏每篇练习将包括
5个选择题 + 2个编程题,将涵盖C语言的不同方面,包括基础语法、数据类型、控制结构、数组、指针和函数等。通过练习,你将逐步掌握C语言的基础知识和常见问题,提高你的编程技巧和解决问题的能力。- 我希望这个博客能够为你提供有价值的练习资源,让你在实践中不断进步。同时,我们也鼓励你在练习过程中进行思考和创新,尝试使用不同的编程方法和技巧。
- 让我们一起挑战C语言练习题,攻克每一个难点,不断提升自己的编程技能!
在评论区分享你的练习心得和问题,与我们一起交流和成长。
🌴选择题
- 以下程序段的输出结果是( )
#include<stdio.h>
int main()
{char s[] = "\\123456\123456\t";printf("%d\n", strlen(s));return 0;
}
A: 12 B: 13 C: 16 D: 以上都不对

🔎正确答案:
A
【解析】:
这里考查转义字符,注意:\ \ 表示字符 ’ \ ',\123 表示字符 ‘{’,\t 表示制表符,这些都是一个字符。
- 若有以下程序,则运行后的输出结果是( )
#include <stdio.h>
#define N 2
#define M N + 1
#define NUM (M + 1) * M / 2
int main()
{printf("%d\n", NUM);return 0;
}
A: 4 B: 8 C: 9 D: 6

🔎正确答案:
B
【解析】:
宏只是替换,替换后NUM的样子是(2+1+1)*2+1/2,计算得8。
- 如下函数的 f(1) 的值为( )
int f(int n)
{static int i = 1;if (n >= 5)return n;n = n + i;i++;return f(n);
}
A: 5 B: 6 C: 7 D: 8

🔎正确答案:
C
【解析】:
此题注意静态局部变量的使用,static改变了i的生命周期,第一次调用函数:i初值是1,递归第二次调用函数时,i还是第一次那个变量,值已经变成了2,再一次调用函数时i就是3,依次类推.
- 下面3段程序代码的效果一样吗( )
int b;
(1)const int* a = &b;
(2)int const* a = &b;
(3)int* const a = &b;
A: (2)=(3) B: (1)=(2) C: 都不一样 D: 都一样
🔎正确答案:
B
【解析】:
const在*的左边,则指针指向的变量的值不可直接通过指针改变(可以通过其他途径改变);在*的右边,则指针的指向不可变。简记为 “左定值,右定向” ,(1)和(2)const都在*的左边,(3)中const在*的右边,所以应该选择B。
- 对于下面的说法,
正确的是( )
A: 对于 struct X{short s;int i;char c;},sizeof ( X )等于sizeof ( s ) + sizeof ( i ) + sizeof ( c )
B: 对于某个double变量 a,可以使用 a == 0.0 来判断其是否为零
C: 初始化方式 char a[14] = “Hello, world!”; 和char a[14]; a = “Hello, world!”;的效果相同
D: 以上说法都不对
🔎正确答案:
D
【解析】:
- A选项,没有考虑内存对齐。
- B选项,考察
double类型的比较,由于浮点数存在误差,不能直接判断两个数是否相等,通常 采用比较两数之差的绝对值是否小于一个很小的数字(具体的可自己设定这样一个数,作为误差)来确定是否相等。- C选项,
a为数组首地址是常量不能改变,- 所以A,B,C都是错的,选择D
🌴编程题
📌尼科彻斯定理
【牛客网链接:HJ76 尼科彻斯定理】
【题目信息】:

【答案解析】:
- 这道题的关键在于知道规律后,能够找到第
n个数据立方的起始奇数,从这个起始奇数开始,组成连续的n个奇数
项之和的表达式即可。 - 比如: 33 的起始奇数是 7 , 则 {7, 9, 11} 3个奇数求和表达式 7 + 9 + 11 。
而起始奇数有个规则: m3 的起始奇数值等于 m * (m - 1) + 1
奇数起始项规律:
首先所有奇数项构成一个差值为2的等差数列, 1 3 5 7 9 ....
其次,1的起始奇数是第1个等差数列项,2的起始奇数是第2个等差数列项,3的起始奇数是第4个等差数列项...
形成规律:
1 2 4 7....,而他们的差值分别是1 2 3 4 5...,所以第n项的起始奇数就是一个从1开始到n-1的等差数列(1 2 3 4 5....)之和+1
因此,
当需要求m的立方的起始奇数时,首先计算他的第一个奇数项是总体的第几个,然后再根据等差数列(1 3 5 7 9...)求这个起始奇数。
等差数列求和公式 Sn=n(a1+an)/2 ---> m * (m - 1) / 2 (计算奇数项是总体的第几个)
等差数列第n项公式 an=a1+(n-1)d ---> 1 + ((m * (m - 1) / 2) + 1 - 1) * 2 (计算这个起始奇数的值)
最终得到m的立方的表达式起始奇数: m * (m - 1) + 1 (最终的表达式)
//代码 1:
#include <stdio.h>
int main() {int m = 0;while (scanf("%d", &m) != EOF) {int start = m * m - m + 1;//找到起始奇数printf("%d", start);//先打印出起始奇数for (int i = 1; i < m; i++) //依次打印后面连续的m-1个奇数{printf("+%d", start + 2 * i);}printf("\n");}return 0;
}//代码 2:
#include <stdio.h>
int main()
{int m;while (~scanf("%d", &m)) {int start = m * (m - 1) + 1;//找到对应m^3的起始奇数char buf[10240] = { 0 };//sprintf(buf, format, ...) 与printf用法类似,格式化字符串但是不用于打印而是放到一个buf数组中sprintf(buf, "%d", start);//先将起始奇数转换成为字符串存入buf中for (int i = 1; i < m; i++) {//然后将紧随其后的m-1个奇数数字转换为字符串,按照指定格式放入buf中//%s+%d, 要求先有一个字符串,然后是+符号,然后是个数字的格式;buf对应原先的数据,start += 2对应紧随其后的奇数sprintf(buf, "%s+%d", buf, start += 2);}printf("%s\n", buf);} return 0;
}
【拓展】:sprintf 函数

下面是一些使用sprintf的例子:
- 基本的格式化
#include <stdio.h>int main() {char buffer[50];int a = 10;float b = 3.14;sprintf(buffer, "整数是 %d, 浮点数是 %f", a, b);printf("%s\n", buffer); // 输出: 整数是 10, 浮点数是 3.140000return 0;
}
- 使用标志符
#include <stdio.h>int main() {char buffer[50];int a = 10;float b = 3.14;sprintf(buffer, "整数是 %2d, 浮点数是 %6.2f", a, b);printf("%s\n", buffer); // 输出: 整数是 10, 浮点数是 3.1400return 0;
}
在这个例子中,%2d表示将整数输出为至少两位的数,如果不足两位则在前面补一个空格。%6.2f表示将浮点数输出为至少6位的数,其中小数点后有两位,如果不足则补0。
这只是sprintf函数的基本用法,实际上它还有许多更复杂的用法和标志符,可以用来处理各种复杂的字符串格式化需求。
📌等差数列
【牛客网链接:HJ100 等差数列】
【题目信息】:

【答案解析】:
- 这道题了解了等差数列求和公式
Sn=n(a1+an)/2就简单了 ,根据题目得知a1=2,而等差数列第n项也有具体公式
an=a1+(n-1)d,而公差为3, 这时候只需要套入公式计算即可。
#include <stdio.h>
int main()
{int n, a1 = 2;while (~scanf("%d", &n)) {int an = a1 + (n - 1) * 3;//等差数列第n项计算printf("%d\n", n * (a1 + an) / 2); //等差数列求和打印} return 0;
}
- 这题也可以遍历一遍等差数列,依次求和。
#include<stdio.h>
int main() {int n;while (EOF != scanf("%d", &n)) {int sum = 0;for (int i = 2; i <3* n+2; i+=3) //等差数列第n项的值为3*(n-1)+2{sum += i;//计算前n项和}printf("%d\n", sum);}return 0;
}
🔥今天的内容就到这里了,有什么问题的话欢迎大家在评论区讨论,也可以私信博主为你解答,如果觉得博主的文章还不错的话, 请👍三连支持一下博主哦🤞

相关文章:

C语言练习题解析:挑战与突破,开启编程新篇章!(2)
💓博客主页:江池俊的博客⏩收录专栏:C语言刷题专栏👉专栏推荐:✅C语言初阶之路 ✅C语言进阶之路💻代码仓库:江池俊的代码仓库🎉欢迎大家点赞👍评论📝收藏⭐ 文…...

sqlite3 加密访问
关于sqlite3 加密 一、相关加密用到的sqlcipher 1.1 sqlcipher 是一个数据库加密的开源库 sqlcipher开源地址 我这边是使用的docker镜像,镜像地址: https://hub.docker.com/r/pallocchi/sqlcipher 加密格式 docker run -v <workdir>:/sqlcip…...

clickhouse 系列1:clickhouse v21.7.5.29 源码编译
1.gcc10安装 安装依赖 yum update yum install -y gcc gcc-c++ yum install -y bzip2 下载gcc 源码包并解压 wget -P /data/base https://mirrors.aliyun.com/gnu/gcc/gcc-10.2.0/gcc-10.2.0.tar.gz cd /data/base && tar -xzvf /data/base/gcc-...

servlet初体验之环境搭建!!!
我们需要用到tomcat服务器,咩有下载的小伙伴看过来:如何正确下载tomcat???_明天更新的博客-CSDN博客 1. 创建普通的Java项目,并在项目中创建libs目录存放第三方的jar包。 建立普通项目 创建libs目录存放第三…...

宁芝 NIZ 键盘开机需要重新插拔 USB 线才能使用
宁芝 NIZ 键盘开机需要重新插拔 USB 线才能使用 问题描述 宁芝 NIZ 键盘开机后无法识别到键盘,需要重新插拔 USB 线才能使用。 解决方法 按住 Fn BackSpaceE 键 5 秒,键盘会切换模式, 状态灯闪 1 次为 USB 接口;状态灯闪 2 次为 PS / 2 …...

R编程教程_编程入门自学教程_菜鸟教程-免费教程分享
教程简介 R是用于统计分析、绘图的语言和操作环境。R是属于GNU系统的一个自由、免费、源代码开放的软件,它是一个用于统计计算和统计制图的优秀工具。R语言的核心是解释计算机语言,其允许分支和循环以及使用函数的模块化编程。 R语言允许与以Cÿ…...

[CMake教程] CMake列表 - list
目录 零、简介一、Reading二、Search三、Modification四、Ordering 零、简介 列表在CMake中大量使用。初始化列表语法如下: set(myList a b c) # Creates the list "a;b;c"归根结底,列表只是一个由分号分隔列表项的单个字符串,这…...
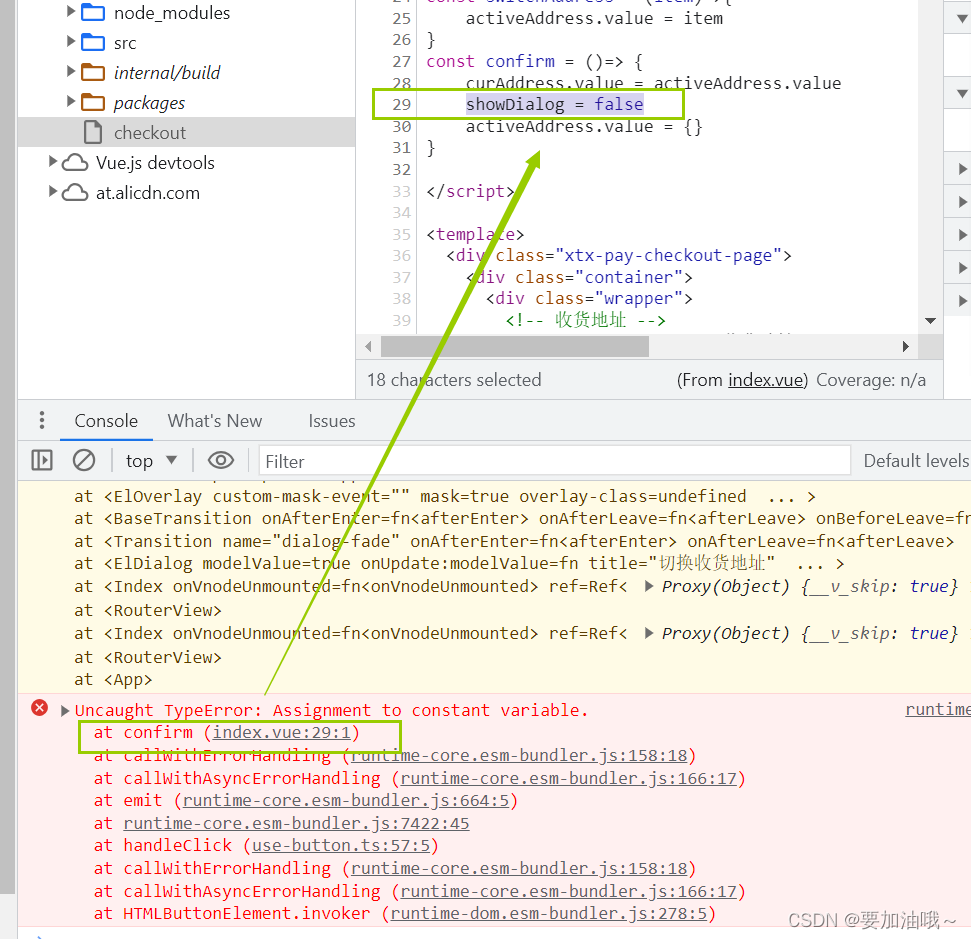
报错 - net::ERR_ABORTED 500 (Internal Server Error)
报错:net::ERR_ABORTED 500 (Internal Server Error) 根据提示找到对应文件 解决:检查代码,根据高亮颜色判断,发现箭头函数漏了一个>。 报错:Uncaught TypeError: Assignment to constant variable. 原因&#x…...

【Java Easypoi Apache poi】 Word导入与导出
引入依赖 <dependency><groupId>cn.afterturn</groupId><artifactId>easypoi-spring-boot-starter</artifactId> </dependency> <!-- 下面的版本需要对应上面依赖中的版本 否则可能会起冲突 --> <!-- 下面的依赖主要是为了使用A…...
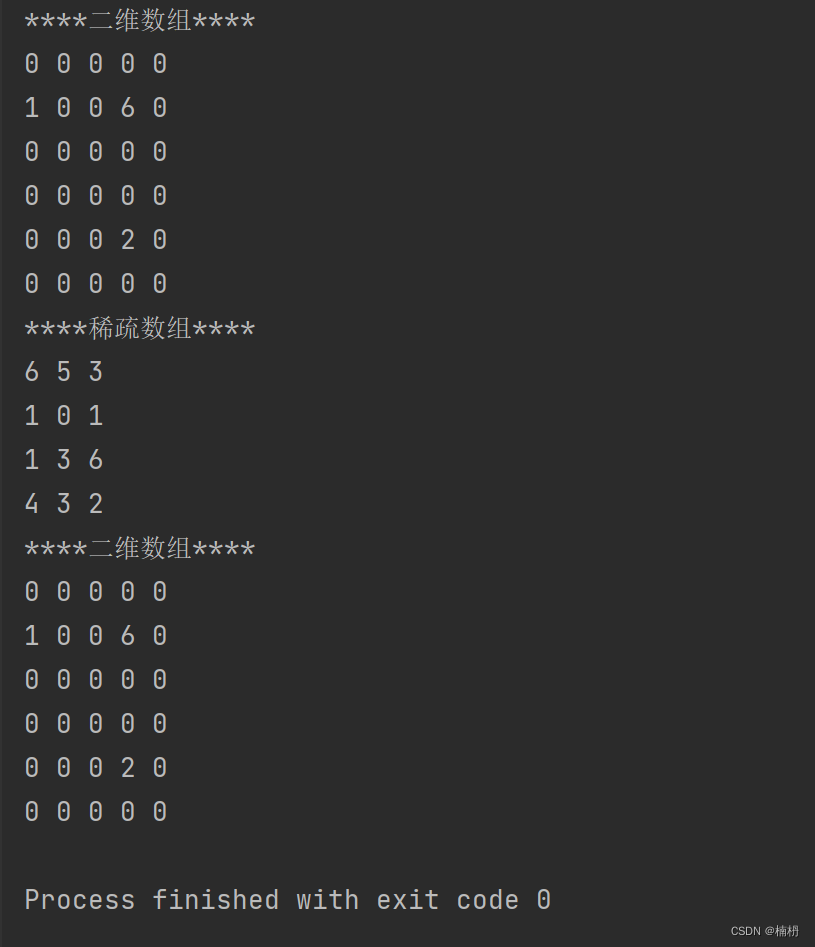
Java稀疏数组
目录 1.稀疏数组 2.稀疏数组的使用 2.1 二维数组转换为稀疏数组 2.2 稀疏数组转换为二维数组 1.稀疏数组 稀疏数组(Sparse Array):当一个数组中的大部分元素为相同的值,可使用稀疏数组来保存该数组,可以将稀疏数组…...

内存管理框架 --- 基础知识
文章目录 一、内存管理1.1 内存管理的出现1.2 内存管理的用途1.2.1 虚拟内存和物理内存的定义1.2.1.1 什么是虚拟内存? 1.2.2 虚拟内存的划分:用户空间与内核空间 1.3 操作系统和MMU1.3.1 OS和MMU的关系1.3.2 虚拟地址到物理地址的映射流程 1.4 物理内存…...

React + Next.js 搭建项目(配有对比介绍一起食用)
文章标题 01 Next.js 是什么02 Next.js 搭建工具 create-next-app03 create-react-app 与 create-next-app 的区别04 快速构建 Next.js 项目05 App Router 与 Pages Router 的区别 01 Next.js 是什么 Next.js 是一个 React 框架,它允许你使用 React 框架建立超强的…...

【Java】Java基础
环境准备 安装JDK和JRE 下载JDK,可以在官网Java Downloads | Oracle 中国下载,但是这里需要注册才能够下载。在Index of java-local/jdk (huaweicloud.com)也可以下载到,但是版本比较老,关系不大,直接下载࿰…...

Spring-SpringBoot-SpringMVC-MyBatis常见面试题
文章目录 Spring篇springbean是安全的的?什么是AOP你们工作中有用过AOP吗spring中的事务是如何实现的spring中事务失效场景Spring的生命周期spring中的循坏依赖springMVC的执行流程springboot的启动原理常用注解MyBatis执行流程Mybatis是否支持延迟加载?Mybatis的一…...

15.MyCat数据库分片
MyCat 是一个开源的数据库中间件,主要用于将数据库操作请求路由和分发到后端的多个数据库节点。 1.Mycat环境搭建 在两个不同数据库中创建相同表 下载mycat https://github.com/MyCATApache/Mycat-Serverhttps://github.com/MyCATApache/Mycat-Server 将下…...

【Python】PySpark
前言 Apache Spark是用于大规模数据(large-scala data)处理的统一(unified)分析引擎。 简单来说,Spark是一款分布式的计算框架,用于调度成百上千的服务器集群,计算TB、PB乃至EB级别的海量数据…...

pycharm 打开Terminal时报错activate.ps1,因为在此系统上禁止运行脚本,并因此无法进入虚拟环境
pycharm 打开Terminal时报错activate.ps1,因为在此系统上禁止运行脚本,并因此无法进入虚拟环境 如下图所示: 网上说可以set_restrictFalse什么的,虽然也可但可能会降低电脑安全性,可以将下面的终端改为cmd.exe即可...

[C++][C#]yolox TensorRT C++ C#部署
YOLOX是一种新型的高性能探测器,由开发者Zheng Ge、Songtao Liu、Feng Wang、Zeming Li和Jian Sun在《YOLOX: Exceeding YOLO Series in 2021》首次提出。与YOLOV5和YOLOV8相比,YOLOX具有更高的性能和更好的平衡,在速度和精度方面都表现出优越…...

根据源码,模拟实现 RabbitMQ - 网络通讯设计,自定义应用层协议,实现 BrokerServer (8)
目录 一、网络通讯协议设计 1.1、交互模型 1.2、自定义应用层协议 1.2.1、请求和响应格式约定 编辑 1.2.2、参数说明 1.2.3、具体例子 1.2.4、特殊栗子 1.3、实现 BrokerServer 1.3.1、属性和构造 1.3.2、启动 BrokerServer 1.3.3、停止 BrokerServer 1.3.4、处…...
MongoDB入门
简介 MongoDB是一个开源、高性能、支持海量数据存储的文档型数据库 是NoSQL数据库产品中的一种,是最像关系型数据库(MySQL)的非关系型数据库 内部采用BSON(二进制JSON)格式来存储数据,并支持水平扩展。 MongoDB本身并不是完全免费的,它对于…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
