哈希的应用——布隆过滤器
✅<1>主页::我的代码爱吃辣
📃<2>知识讲解:数据结构——位图
☂️<3>开发环境:Visual Studio 2022
💬<4>前言:布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
目录
一.布隆过滤器提出
二.布隆过滤器概念
三.布隆过滤器实现
1.布隆过滤器的结构
2.布隆过滤器插入
3.布隆过滤器的查询
4.布隆过滤器的删除
四.布隆过滤器优点
五.布隆过滤器缺陷
六.海量数据处理

一.布隆过滤器提出
我们在使用新闻客户端看新闻时,它会给我们不停地推荐新的内容,它每次推荐时要去重,去掉
那些已经看过的内容。问题来了,新闻客户端推荐系统如何实现推送去重的? 用服务器记录了用
户看过的所有历史记录,当推荐系统推荐新闻时会从每个用户的历史记录里进行筛选,过滤掉那
些已经存在的记录。 如何快速查找呢?
- 用哈希表存储用户记录,缺点:浪费空间
- 用位图存储用户记录,缺点:位图一般只能处理整形,如果内容编号是字符串,就无法处理了。
- 将哈希与位图结合,即布隆过滤器。
二.布隆过滤器概念
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概
率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存
在”,它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也
可以节省大量的内存空间。
三.布隆过滤器实现
1.布隆过滤器的结构
template<size_t N,class K=string,class Hash1= HashChange1,class Hash2=HashChange2 ,class Hash3=HashChange3>
class Bloom
{Hash1 hash1;Hash2 hash2;Hash3 hash3;
public:void set(const K key){}bool test(const K key){}private:static const size_t _X = 5;//存储数据个数和hash函数个数的一种关系,使得冲突率降到最低BitSet<N*_X> _bit; //位图共开N*_x个位
};注意:
static const size_t _X = 5;//存储数据个数和hash函数个数的一种关系,使得冲突率降到最低
BitSet<N*_X> _bit; //位图共开N*_x个位
具体介绍见详解布隆过滤器的原理,使用场景和注意事项 - 知乎。
2.布隆过滤器插入
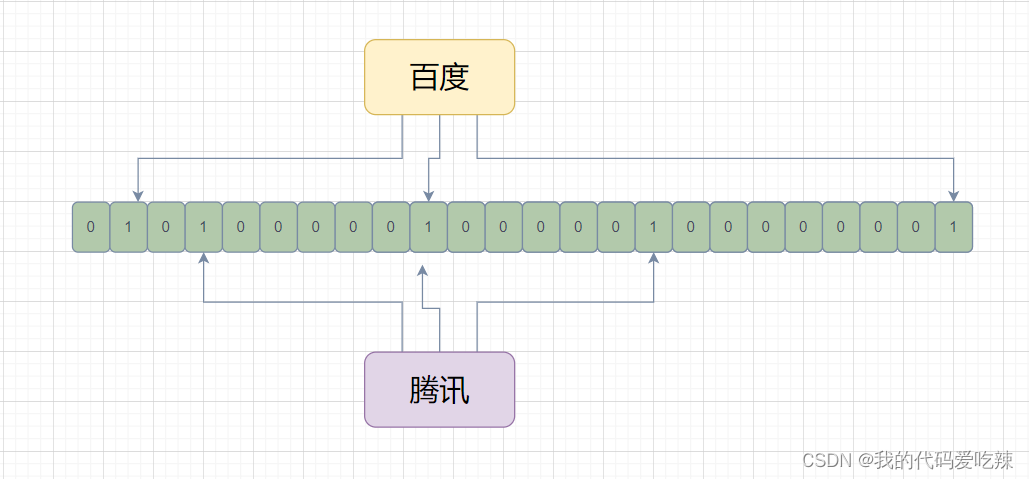
向布隆过滤器插入“百度”,“Tencent”

struct HashChange1
{size_t operator()(const string& str){size_t hash = 0;for (auto ch : str){hash += ch;hash *= 31;}return hash;}
};struct HashChange2
{size_t operator()(const string& str){size_t hash = 0;for (long i = 0; i < str.size(); i++){size_t ch = str[i];if ((i & 1) == 0){hash ^= ((hash << 7) ^ ch ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));}}return hash;}
};struct HashChange3
{size_t operator()(const string& str){size_t hash = 5381;for (auto ch : str){hash += (hash << 5) + ch;}return hash;}
};template<size_t N,class K=string,class Hash1= HashChange1,class Hash2=HashChange2 ,class Hash3=HashChange3>
class Bloom
{Hash1 hash1;Hash2 hash2;Hash3 hash3;
public:void set(const K key){//分别使用三个hash函数分别插入三个位置_bit.set(hash1(key) % (_X * N));_bit.set(hash2(key) % (_X * N));_bit.set(hash3(key) % (_X * N));}bool test(const K key){}private:static const size_t _X = 5;BitSet<N*_X> _bit;
};3.布隆过滤器的查询
布隆过滤器的思想是将一个元素用多个哈希函数映射到一个位图中,因此被映射到的位置的比特
位一定为1。所以可以按照以下方式进行查找:分别计算每个哈希值对应的比特位置存储的是否为
零,只要有一个为零,代表该元素一定不在哈希表中,否则可能在哈希表中。
注意:布隆过滤器如果说某个元素不存在时,该元素一定不存在,如果该元素存在时,该元素可
能存在,因为有些哈希函数存在一定的误判。
例如:
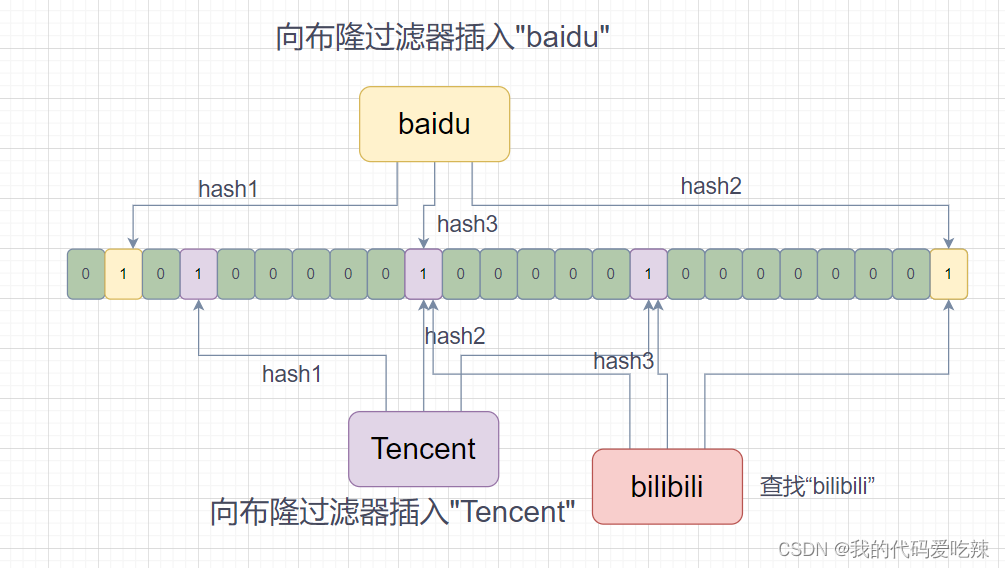
如果此时我们查询“bilibili”,即使我们没有插入"bilibili",也会得到一个存在的反馈,所以说存在的反馈是不准确的,但是如果我们得到的反馈是不存在,那就一定不存在。
bool test(const K key){//当有一个位置不存在时就是准确的不存在if (!_bit.test(hash1(key) % (_X * N))){return false;}if (!_bit.test(hash2(key) % (_X * N))){return false;}if (!_bit.test(hash3(key) % (_X * N))){return false;}return true;//不准确,存在误判}4.布隆过滤器的删除
布隆过滤器不能直接支持删除工作,因为在删除一个元素时,可能会影响其他元素。
比如:删除上图中"tencent"元素,如果直接将该元素所对应的二进制比特位置0,“baidu”元素也
被删除了,因为这两个元素在多个哈希函数计算出的比特位上刚好有重叠。
一种支持删除的方法:将布隆过滤器中的每个比特位扩展成一个小的计数器,插入元素时给k个计
数器(k个哈希函数计算出的哈希地址)加一,删除元素时,给k个计数器减一,通过多占用几倍存储
空间的代价来增加删除操作。
四.布隆过滤器优点
- 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关。
- 哈希函数相互之间没有关系,方便硬件并行运算。
- 布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势。
- 在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势。
- 数据量很大时,布隆过滤器可以表示全集,其他数据结构不能。
- 使用同一组散列函数的布隆过滤器可以进行交、并、差运算。
五.布隆过滤器缺陷
- 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白名单,存储可能会误判的数据)。
- 不能获取元素本身。
- 一般情况下不能从布隆过滤器中删除元素。
六.布隆过滤器实现源码:
BitSet.hpp
#include<vector>
#include<iostream>
#include<string>
using namespace std;template<size_t N>
class BitSet
{
public:BitSet(){_map.resize((N / 8) + 1, 0);}void set(const int num){size_t i = num / 8;size_t j = num % 8;_map[i] |= 1 << j;}void reset(const int num){size_t i = num / 8;size_t j = num % 8;_map[i] &= ~(1 << j);}bool test(const int num){size_t i = num / 8;size_t j = num % 8;return _map[i] & (1 << j) ;}private:vector<char> _map;
};
Bloom.hpp
#pragma once
#include"BitMap.hpp"struct HashChange1
{size_t operator()(const string& str){size_t hash = 0;for (auto ch : str){hash += ch;hash *= 31;}return hash;}
};struct HashChange2
{size_t operator()(const string& str){size_t hash = 0;for (long i = 0; i < str.size(); i++){size_t ch = str[i];if ((i & 1) == 0){hash ^= ((hash << 7) ^ ch ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));}}return hash;}
};struct HashChange3
{size_t operator()(const string& str){size_t hash = 5381;for (auto ch : str){hash += (hash << 5) + ch;}return hash;}
};template<size_t N,class K=string,class Hash1= HashChange1,class Hash2=HashChange2 ,class Hash3=HashChange3>
class Bloom
{Hash1 hash1;Hash2 hash2;Hash3 hash3;
public:void set(const K key){_bit.set(hash1(key) % (_X * N));_bit.set(hash2(key) % (_X * N));_bit.set(hash3(key) % (_X * N));}bool test(const K key){//当有一个位置不存在时就是准确的不存在if (!_bit.test(hash1(key) % (_X * N))){return false;}if (!_bit.test(hash2(key) % (_X * N))){return false;}if (!_bit.test(hash3(key) % (_X * N))){return false;}return true;//不准确,存在误判}private:static const size_t _X = 5;BitSet<N*_X> _bit;
};七.海量数据处理
1. 给定100亿个整数,设计算法找到只出现一次的整数?
答:我们要标识一个整数的状态,此时应该由三种:
- 一次也没有出现
- 只出现一次
- 出现次数在一次以上
我们使用两张位图即可,每个数值就会由两个比特位进行标识,两个比特位就可以标识这三种状态:
- 一次也没有出现:00
- 只出现一次:01
- 出现次数在一次以上:10
2.给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
方法一:我们将第一个文件插入位图,用第二个文件对第一个文件的位图进行查询,查询到了就是交集数据。如果文件中都有重复数据,就会对重复文件反复找到交集,我们可以每次,找到交集以后将上面一个位图交集位置置0,就不会下一次再重复找到交集了。
方法二:将两个文件的数据,全部加载带位图,在对两个位图按位与,交集位置都是1,按位与之后得到的就是交集。
3.位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
这个问题与第一个问题相似,想找到出现次数不超过两次的数据,我们就看需要几个状态进行标识,进而选择使用几张位图即可。不超过2次即需要4中状态标识:
- 一次也没有出现:00
- 出现一次:01
- 出现两次:10
- 出现两次以上:11
问题迎刃而解。
4.给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?
首先我们使用hash切割:针对A,B文件分别创建1000个小文件Ai,Bi(1<i<1000)。对文件A和文件B的每个query进行hash分割,分割就是对每一个query执行哈希函数,得到一个hash位置 i 控制在1000以内,然后进入Ai和Bi文件中。A和B相同的query因为使用同一个hash函数,就会得到同一个hash位置i,继而进入编号一样的小文件。
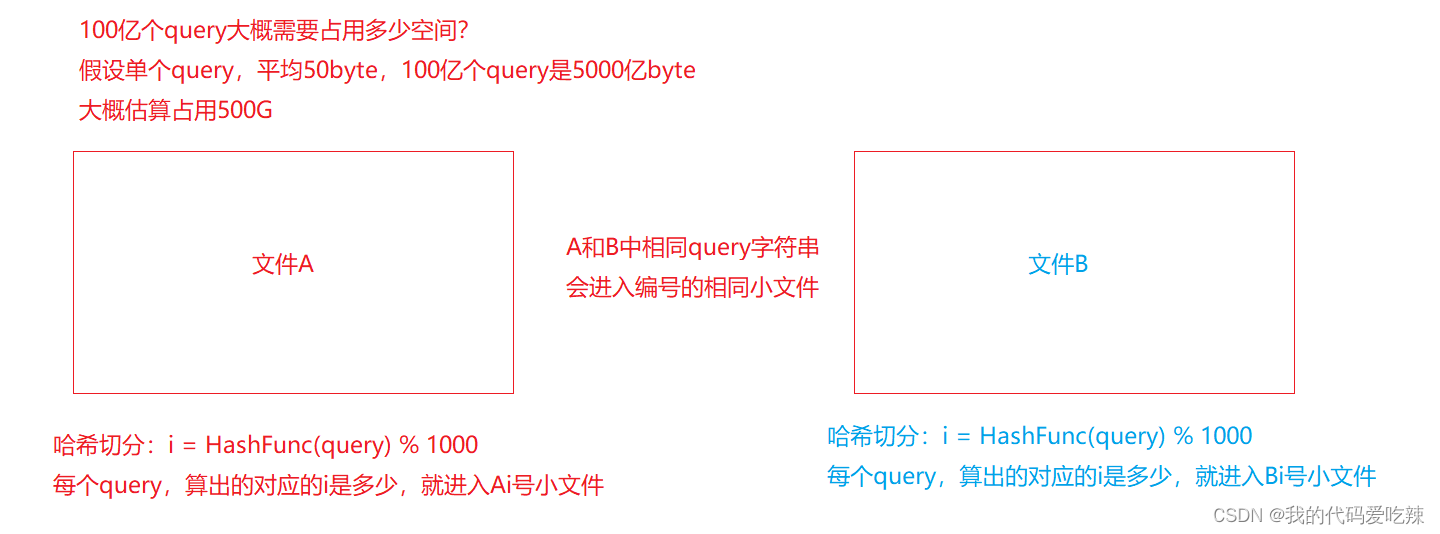

如果我们在hash分割小文间的时候,出现某一个小文件过大:

相关文章:

哈希的应用——布隆过滤器
✅<1>主页::我的代码爱吃辣 📃<2>知识讲解:数据结构——位图 ☂️<3>开发环境:Visual Studio 2022 💬<4>前言:布隆过滤器是由布隆(Burton Howard Bloom&…...

LNMT的多机部署和双机热备
目录 一、环境 二、配置tomcat 三、配置nfs共享 四、配置nginx 1、两台都需要折磨配置 2、在http下面插入这两条信息 五、配置keepalived 1、安装 2、重新启动一下keepalived查看IP 六、验证双机热备 1、查看调度器备的IP,ip漂移说明keepalived生效 2、访…...

软件测试/测试开发丨Pytest和Allure报告 学习笔记
点此获取更多相关资料 本文为霍格沃兹测试开发学社学员学习笔记分享 原文链接:https://ceshiren.com/t/topic/26755 Pytest 命名规则 类型规则文件test_开头 或者 _test 结尾类Test 开头方法/函数test_开头注意:测试类中不可以添加__init__构造函数 注…...
十七、命令模式
一、什么是命令模式 命令(Command)模式的定义:将一个请求封装为一个对象,使发出请求的责任和执行请求的责任分割开。这样两者之间通过命令对象进行沟通,这样方便将命令对象进行储存、传递、调用、增加与管理。 命令…...

服务器安装 anaconda 及 conda: command not found [解决方案]
[解决方案] conda: command not found Anaconda3 安装conda: command not found Anaconda3 安装 由于连接的服务器,无法直接在anaconda官网上下载安装文件,所以使用如下方法: wget https://repo.anaconda.com/archive/Anaconda3-2023.03-Li…...
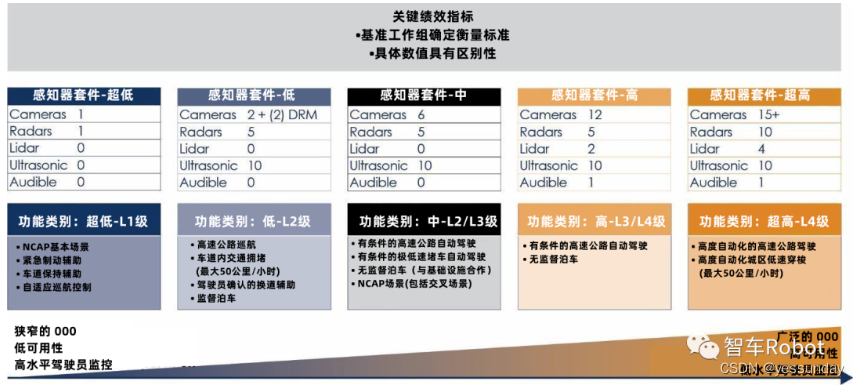
自动驾驶和辅助驾驶系统的概念性架构(二)
摘要: 本篇为第二部分主要介绍底层计算单元、示例工作负载 前言 本文档参考自动驾驶计算联盟(Autonomous Vehicle Computing Consortium)关于自动驾驶和辅助驾驶计算系统的概念系统架构。该架构旨在与SAE L1-L5级别的自动驾驶保持一致。本文主要介绍包括功能模块图…...
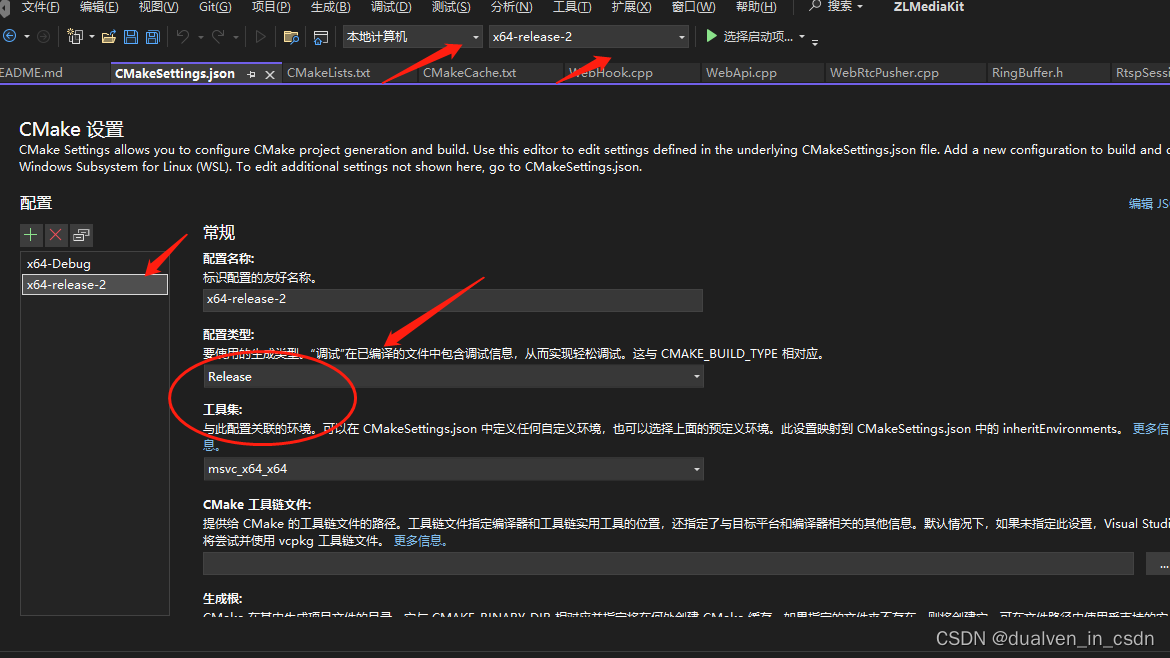
【c++】VC编译出的版本,发布版本如何使用
目录 使用release类型进行发布 应用程序无法正常启动 0xc000007b 版本对应 vcruntime140d 应用版本 参考文章 使用release类型进行发布 应用程序无法正常启动 0xc000007b "应用程序无法正常启动 0xc000007b" 错误通常是一个 Windows 应用程序错误…...

自然语言处理(五):子词嵌入(fastText模型)
子词嵌入 在英语中,“helps”“helped”和“helping”等单词都是同一个词“help”的变形形式。“dog”和“dogs”之间的关系与“cat”和“cats”之间的关系相同,“boy”和“boyfriend”之间的关系与“girl”和“girlfriend”之间的关系相同。在法语和西…...
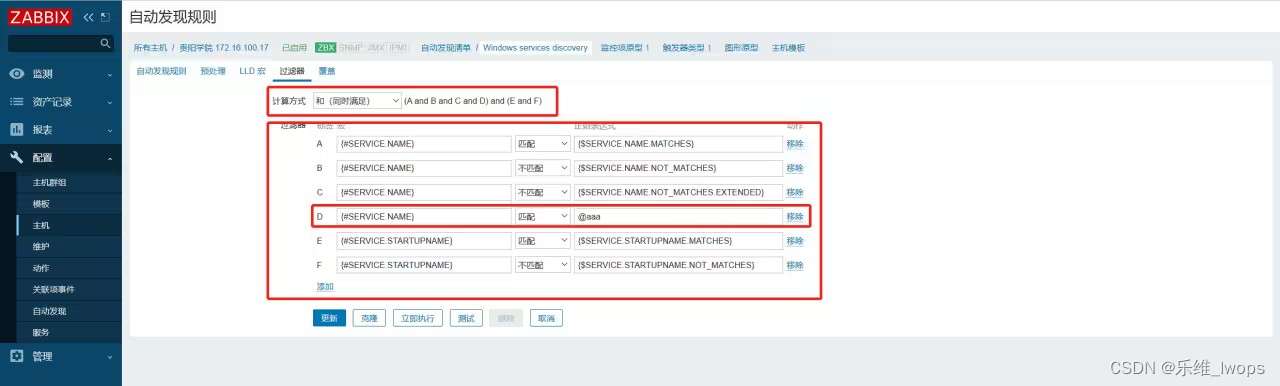
Zabbix“专家坐诊”第202期问答汇总
问题一 Q:请问一下 zabbix 里面怎么能创建出和sh文件有关联的监控项? A: 1.使用 Zabbix Agent 主动模式:如果你在目标主机上安装了 Zabbix Agent,并且想要监控与 sh 文件相关的指标,可以创建一个自定义的…...
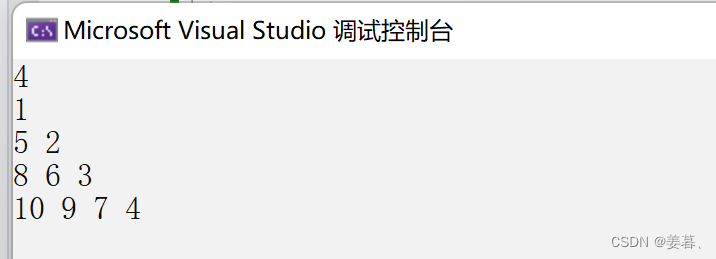
【c语言】输出n行按如下规律排列的数
题述:输出n行按如下规律排列的数 输入: 4(应该指的是n) 输出: 思路: 利用下标的规律求解,考察数组下标的灵活应用,我们可以看出数从1开始是斜着往下放的,那么我们如何利用两层for循环求解这道题ÿ…...

023 - STM32学习笔记 - 扩展外部SDRAM(二) - 扩展外部SDRAM实验
023- STM32学习笔记 - 扩展外部SDRAM(一) - 扩展外部SDRAM实验 本节内容中要配置的引脚很多,如果你用的开发板跟我的不一样,请详细参照STM32规格书中说明对相关GPIO引脚进行配置。 先提前对本届内容的变成步骤进行总结如下&…...

机器学习 | Python实现XGBoost极限梯度提升树模型答疑
机器学习 | MATLAB实现XGBoost极限梯度提升树模型答疑 目录 机器学习 | MATLAB实现XGBoost极限梯度提升树模型答疑问题系列问题回答问题系列 关于XGBoost有几个问题想请教一下。1.XGBoost的API有哪些种调用方法?2.参数如何调? 问题回答 XGBoost的API有2种调用方法,一种是我们…...
关于使用远程工具连接mysql数据库时,提示:Public Key Retrieval is not allowed
我在使用DBeaver工具连接 数据库时,提示:Public Key Retrieval is not allowed, 我在前一天还是可以连接的,但是今天突然无法连接了, 但是最后捣鼓了一下又可以了。 具体方法:首先先把mysql服务停了&#x…...

leetcode做题笔记117. 填充每个节点的下一个右侧节点指针 II
给定一个二叉树: struct Node {int val;Node *left;Node *right;Node *next; } 填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。 初始状态下,所有 next 指针都…...
解决博客不能解析PHP直接下载源码问题
背景: 在网站设置反向代理后,网站突然不能正常访问,而是会直接下载访问文件的PHP源码 解决办法: 由于在搞完反向代理之后,PHP版本变成了纯静态,所以网站不能正常解析;只需要把PHP版本恢复正常…...

voc 转coco
import os import random import shutil import sys import json import glob import xml.etree.ElementTree as ET""" 修改下面3个参数 1.val_files_num : 验证集的数量 2.test_files_num :测试集的数量 3.voc_annotations : voc的annotations路径 …...

【C语言每日一题】03. 对齐输出
题目来源:http://noi.openjudge.cn/ch0101/03/ 03 对齐输出 总时间限制: 1000ms 内存限制: 65536kB 问题描述 读入三个整数,按每个整数占8个字符的宽度,右对齐输出它们。 输入 只有一行,包含三个整数,整数之间以一…...

七大排序完整版
目录 一、直接插入排序 (一)单趟直接插入排 1.分析核心代码 2.完整代码 (二)全部直接插入排 1.分析核心代码 2.完整代码 (三)时间复杂度和空间复杂度 二、希尔排序 (一)对…...

C语言的数据类型简介
一、基本类型 (1)六种基本类型 **字符串常量和字符常量的不同 1)‘a’为字符常量,”a”为字符串常量 2)每个字符串的结尾,编译器会自动添加一个结束标志位‘\0’ “a”包含两个字符’a’和’\0’ &#x…...

Fei-Fei Li-Lecture 16:3D Vision 【斯坦福大学李飞飞CV课程第16讲:3D Vision】
目录 P1 2D Detection and Segmentation P2 Video 2D time series P3 Focus on Two Problems P4 Many more topics in 3D Vision P5-10 Multi-View CNN P11 Experiments – Classification & Retrieval P12 3D Shape Representations P13--17 3D Shape Represen…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
