线性代数的学习和整理13: 定义域,值域,到达域 和单射,满射,双射,反函数,逆矩阵
目录
1 函数与 向量/矩阵
2 初等数学的函数
2.1 函数
2.2 函数的定义:定义域 →映射→ 值域
3 高等数学里的函数:定义域和陪域/到达域(非值域)的映射关系
3.1 函数
3.2 单射,满射,双射等都是针对定义域 和 陪域的
3.3 易错地方:值域较小且是被决定的
3.4 单射,满射,双射
4 函数和反函数 → 矩阵和逆矩阵
4.1 函数和反函数
4.2 矩阵和逆矩阵 (待完善)
1 函数与 向量/矩阵
下面两者形式类似,本质也类似
- 函数的: ax=y ,常规函数里,a,x,y 一般都是单个数
- 矩阵: AX=Y , 矩阵乘法,这里 A,x,y 一般都是向量/矩阵
- 线性代数,就是处理 数组和矩阵(数组的数组)的学科
2 初等数学的函数
2.1 函数
形如 ax=y=f(x)的就是函数
- 自变量 input:x ,原像
- 因变量 output:y=f(x) ,像
- 函数/变化规则/映射法则 function :f
- 定义域domain: 自变量x的取值范围就是定义域,集合x
- 值域 range: 因变量f(x)=y 的取值范围就是值域, 所有x的像的集合?
2.2 函数的定义:定义域 →映射→ 值域
从映射的角度来看,定义域,值域
- 函数定义域里的每个值x,必须有且只有一个值y与之对应
- 每个x不能是0个y对应
- 每个x都必须对应1个y
- 每个x不能对应多个y
- 函数值域里的每个值y,必须有一个定义域的x与之对应
- 每个y都有1个x对应
- 有的y可能都多个x对应到它
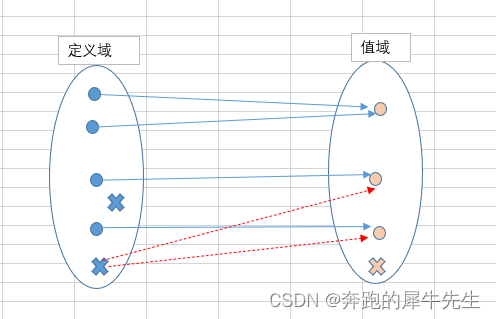
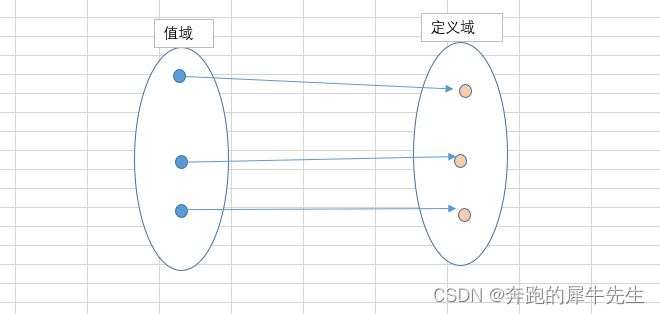
如果从图形上来说
- 函数f(x) 是从定义域 → 值域
- 下面定义域里打叉×的点都是错的
- 下面值域里打叉×的点都是错的
3 高等数学里的函数:定义域和陪域/到达域(非值域)的映射关系
3.1 函数
形如 ax=y=f(x)的就是函数
- 自变量 input:x ,原像
- 因变量 output:y=f(x) ,像
- 函数/变化规则/映射法则 function :f
- 定义域domain: 自变量x的取值范围就是定义域,集合x
- 值域 range: 因变量f(x)=y 的取值范围就是值域, 所有x的像的集合?
- 陪域/ 到达域codomain :因变量f(x)=y 可能的范围,集合y
3.2 单射,满射,双射等都是针对定义域 和 陪域的
- 理清概念
- 这个只针对 定义域 → 陪域/到达域
- 不针对 定义域 → 值域
- 就这么简单粗暴
- 前面的函数的映射定义,可能算初等数学的把
- 这个加入了 陪域/到达域的映射定义,可能算高等函数的把
3.3 易错地方:值域较小且是被决定的
- 定义域,值域取值范围都选 R 或者 R+
- 而值域,一般不存在选范围的问题,因为是同感 y=f(x) 一一映射决定的,一般肯定都是R的一个较小的子集!!
比如提前一个例题
- 为什么y=x^2 不是满射,因为都是针对 定义域 R→ 陪域/到达域R,而值域是R+,因此不是满射
3.4 单射,满射,双射
- 非函数: 定义域里有的x对应了多个y,这种情况还是非函数
- 单射: 定义域里的每个x 都有唯一的y对应。(但是有的y可能没有x对应)
- 非单射: 定义域里的每个x 都有y对应,但是可能对应相同的y
- 满射: 到达域里(非值域)的每个y 都有x对应 (但是有的y可能对应的2个x)
- 非满射: 到达域里(非值域)不是每个y 都有x对应,有些y值没有x映射
- 特例
- 双射: 定义域中的x 和值域中y 分别一一对应
- 双射的意义,只有满秩的双射矩阵,一定可逆矩阵(见下面)
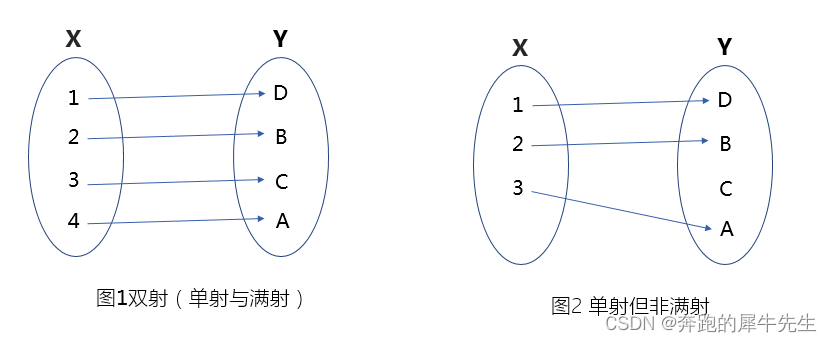
- 单射非满射: 普通单射,只单射,不满射
- 单射&满射: 双射
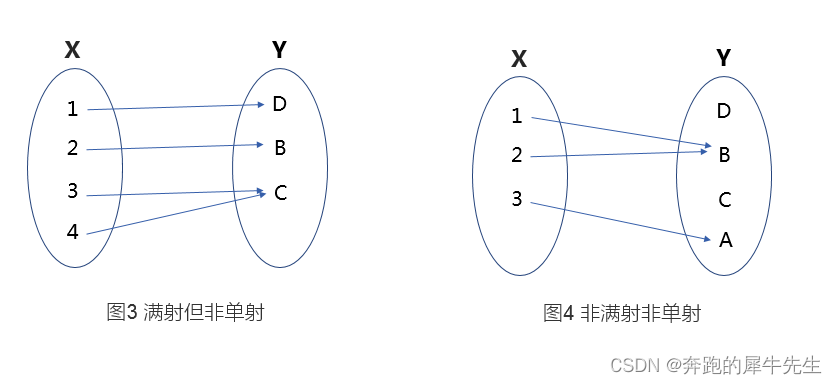
- 非单射&满射:
- 非单射&非满射:
4 函数和反函数 → 矩阵和逆矩阵
双射的意义,只有满秩的双射矩阵,一定可逆矩阵(见下面)
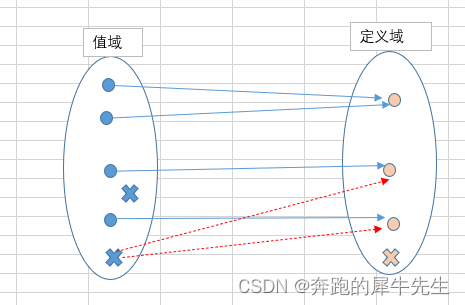
- 普通函数,直接让y 映射到x,很可能就不是函数
- 下面图可以看到,直接让y 映射到x,很可能1个y会映射多个x,这样就不是函数
4.1 函数和反函数
如果一个函数 y=f(x)=ax 反过来 x=f(y)
- 如果x和y调换,如果不是满射,反过来就不是单射,函数就不存在反函数
- 所以 函数必须是 双射,这个函数才会有反函数。
- 双射的函数,一定有反函数,见下图
4.2 矩阵和逆矩阵 (待完善)
- 同理,矩阵必须是满秩的,才会有逆矩阵
- 详细的需要写
相关文章:

线性代数的学习和整理13: 定义域,值域,到达域 和单射,满射,双射,反函数,逆矩阵
目录 1 函数与 向量/矩阵 2 初等数学的函数 2.1 函数 2.2 函数的定义:定义域 →映射→ 值域 3 高等数学里的函数:定义域和陪域/到达域(非值域)的映射关系 3.1 函数 3.2 单射,满射,双射等都是针对…...
深入MaxCompute -第十一弹 -QUALIFY
简介: MaxCompute支持QUALIFY语法过滤Window函数的结果,使得查询语句更简洁易理解。Window函数和QUALIFY语法之间的关系可以类比聚合函数GROUP BY语法和HAVING语法。 MaxCompute(原ODPS)是阿里云自主研发的具有业界领先水平的分…...

Mysql定时备份事件
创建了一个名为backup_database的定时任务,每天自动在当前时间的后一天开始执行。备份数据库的代码使用mysqldump命令将数据库导出为sql文件保存在指定的备份目录中。 需要注意的是,上述代码中的用户名 (username)、密码 (password)、主机名 (hostname) …...

探索ClickHouse——安装和测试
我们在Ubuntu 20 Server版虚拟机上对ClickHouse进行探索。 安装 检测环境 grep -q sse4_2 /proc/cpuinfo && echo "SSE 4.2 supported" || echo "SSE 4.2 not supported"SSE 4.2 supported 可以看到我们的环境支持编译版本的。如果不支持的环境…...
常用的css样式
1:flex布局 .flex-between {display: flex;justify-content: space-between; }.flex-evenly {display: flex;justify-content: space-evenly; }.flex-end {display: flex;justify-content: flex-end; }.flex {display: flex; }.flex-center {display: flex;justify…...
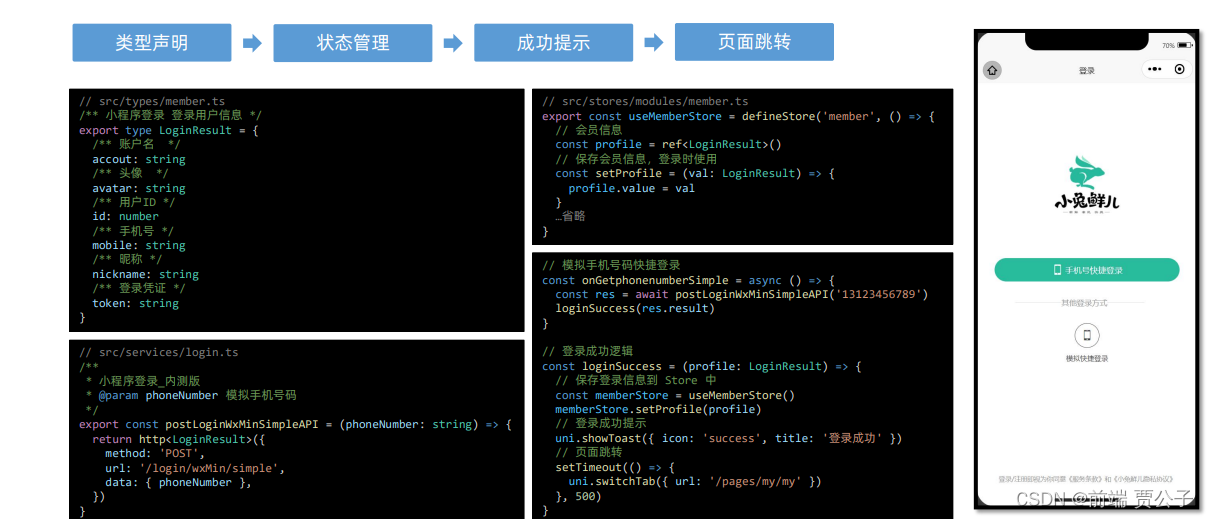
小兔鲜儿 - 微信登录
目录 微信登录 登录方式 静态结构 获取登录凭证 获取手机号码 微信登录接口(生产环境) 模拟手机登录(开发环境) 用户信息持久化存储 涉及知识点:微信授权登录,文件上传,Store 状态管理等。 微信登录 微信小程序的开放…...
)
C++ Primer阅读笔记--对象移动(右值引用、移动迭代器和引用限定符的使用)
目录 1--右值引用 2--std::move 3--移动构造函数 4--移动赋值运算符 5--移动迭代器 6--引用限定符 1--右值引用 右值引用必须绑定到右值的引用,通过 && 获得右值引用; 右值引用只能绑定到临时对象(即将被销毁的对象)…...

【办公类-16-01-02】2023年度上学期“机动班下午代班的排班表——跳过周三、节日和周末”(python 排班表系列)
背景需求: 2023年第一学期(2023年9-2024年1月),我又被安排为“机动班”,根据新学期的校历,手动推算本学期的机动班的带班表 排版原则 1、班级数量:共有6个班级,循环滚动 2、每周次…...

ChatGPT HTML JS Echarts实现热力图展示
热力图是一种常用的数据可视化图表,主要用于展示数据的分布和密度情况。它通过使用不同颜色的热点来表示数据在地理或二维空间上的分布情况,从而直观地显示出数据的密集程度和趋势。 热力图的功能和作用如下: 1. 数据分布展示:热力图可以将大量数据以热点的形式展示在地理…...

JavaScript七小知
文章目录 1. == 和 ===区别2. a++ 和 ++a区别3. 创建js对象的三种方式4. 原型与原型链相关4.1 prototype4.2 __proto__4.3 constructor4.4 原型链5. 定时器的两种设置方式6. 时间相关7. axios与axios拦截器1. == 和 ===区别 == 只是判断值是否一致, === 会判断数据类型和…...
Ubuntu【系统环境下】【编译安装OpenCV】【C++调用系统opencv库】
Ubuntu【系统环境下】【编译安装OpenCV】【C调用系统opencv库】 前言: 本人需要用C写代码,调用OpenCV库,且要求OpenCV版本号大于4.1.0 由于使用的是18.04的版本,所以apt安装OpenCV的版本始终是3.2.0,非常拉胯&#…...

AR界安卓在中国,Rokid引爆空间计算狂潮
击关注 文丨刘雨琦 你可能很难想象,在一个没有显示屏也没有鼠标的空间,仅凭一副AR眼镜和一台口袋主机,就能完成一篇5000字的文章。 没错,8月26日,在2023 Rokid Jungle 新品发布会现场,这样的场景正在真实…...

在 React 中如何使用定时器
在React中使用定时器通常有两种方式:使用setInterval和setTimeout函数。 使用setInterval函数: 首先,在组件中导入useEffect和useState函数: import React, { useEffect, useState } from "react";在组件中声明一个状…...

Unity记录4.6-存储-第四阶段总结
文章首发见博客:https://mwhls.top/4822.html。 无图/格式错误/后续更新请见首发页。 更多更新请到mwhls.top查看 欢迎留言提问或批评建议,私信不回。 汇总:Unity 记录 摘要:存储初步实现的总结 总结-2023/08/19 实现了tile存储&…...
)
【Python】从入门到上头— 使用包、模块、安装第三方模块(7)
一.什么是模块 在Python中,一个.py文件就称之为一个模块(Module)。 模块好处?: 方便重用代码,写完一个通用的模块,可以在很多地方直接拿来用相同名字的函数和变量完全可以分别存在不同的模块中…...
flutter和原生利用pigeon建立通道
首先导入依赖: dependencies: pigeon: ^10.0.0定义一个文件: /// 用于定于flutter和平台的桥接方法 /// HostApi() 标记的,是用于 Flutter 调用原生的方法; /// FlutterApi() 标记的,是用于原生调用 Flutter 的方法&…...
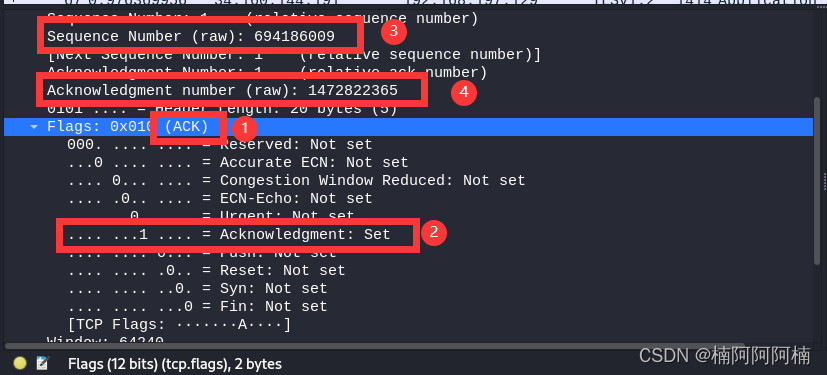
TCP连接分析:探寻TCP的三次握手
文章目录 一、实验背景与目的二、实验需求三、实验解法1. 预先抓包监测使用Wireshark工具2.进行TCP三次握手,访问www.baidu.com3.分析Wireshark捕获的TCP包 摘要: 本实验使用Wireshark工具,通过抓包监测和分析,深入研究了与百度服…...

gitHooks使用教程
1. 安装所需依赖 npm install eslint prettier husky lint-staged --save-dev 2.初始化 husky npx husky-init && npm install 这将创建一个 .husky/ 目录,并且在其中包含一个示例的 pre-commit 文件。 3.设置 pre-commit 钩子 npx husky add .husky/…...

2023.8 - java - 数组
声明数组变量 首先必须声明数组变量,才能在程序中使用数组。下面是声明数组变量的语法: dataType[] arrayRefVar; // 首选的方法或dataType arrayRefVar[]; // 效果相同,但不是首选方法int[] a {1,2,3};int b[] new int[10];TS:let a:…...

ChatGPT怎么辅助解决社会问题?
ChatGPT作为一个强大的自然语言处理模型,具有潜力辅助解决多种社会问题。其能力可以应用于信息传递、教育、宣传、意识提高等领域,为社会问题的解决提供支持。以下将详细探讨ChatGPT如何辅助解决社会问题。 **1. 教育与意识提高**: ChatGPT可…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
