数学建模:TOPSIS分析
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛
TOPSIS分析法
算法流程
- 假设有m个评价对象,n个评价指标,首先需要进行指标的正向化:
- 极大型
- 极小型
- 单点型
- 区间型
- 然后对正向化后的矩阵进行标准化,得到 Z Z Z 矩阵:假设 X X X 为正向化后的矩阵,则 Z Z Z 是标准化后的矩阵:
X = [ x 11 x 11 . . . x 1 n x 21 x 22 . . . x 2 n ⋮ ⋮ ⋱ ⋮ x m 1 x m 2 . . . x m n ] ; X=\begin{bmatrix}x_{11}&x_{11}&...&x_{1n}\\x_{21}&x_{22}&...&x_{2n}\\\vdots&\vdots&\ddots&\vdots\\x_{m1}&x_{m2}&...&x_{mn}\end{bmatrix}; X= x11x21⋮xm1x11x22⋮xm2......⋱...x1nx2n⋮xmn ;
Z i j = x i j ∑ i = 1 n x i j 2 Z_{ij}=\frac{x_{ij}}{\sqrt{\sum_{i=1}^nx_{ij}^2}} Zij=∑i=1nxij2xij
- 得到标准化后的矩阵后,我们要进行打分:计算出第 i i i个评价对象与最大值的距离 D i + D^{+}_i Di+ ,和最小值的距离 D i − D^{-}_i Di−
- 计算带组合权重的 TOPSIS 分析法还需要 D i + D^{+}_i Di+ D i − D^{-}_i Di− 分别再乘以权重 W W W
然后再开方。
- 计算带组合权重的 TOPSIS 分析法还需要 D i + D^{+}_i Di+ D i − D^{-}_i Di− 分别再乘以权重 W W W
Z = [ z 11 z 11 . . . z 1 n z 21 z 22 . . . z 2 n ⋮ ⋮ ⋱ ⋮ z m 1 z m 2 . . . z m n ] ; Z=\begin{bmatrix}z_{11}&z_{11}&...&z_{1n}\\z_{21}&z_{22}&...&z_{2n}\\\vdots&\vdots&\ddots&\vdots\\z_{m1}&z_{m2}&...&z_{mn}\end{bmatrix}; Z= z11z21⋮zm1z11z22⋮zm2......⋱...z1nz2n⋮zmn ;
最大值 ( z 1 + , z 2 + . . . z n + ) = ( max { z 11 , z 21 , . . . , z m 1 } , max { z 12 , z 22 , . . . , z m 2 } , . . . , max { z 1 n , z 2 n , . . . , z m n } ) ∣ 最大值(z^{+}_1,z^{+}_2 ...z^{+}_n) = \left.\left(\max\begin{Bmatrix}z_{11},z_{21},...,z_{m1}\end{Bmatrix},\max\begin{Bmatrix}z_{12},z_{22},...,z_{m2}\end{Bmatrix},...,\max\begin{Bmatrix}z_{1n},z_{2n},...,z_{mn}\end{Bmatrix}\right)\right| 最大值(z1+,z2+...zn+)=(max{z11,z21,...,zm1},max{z12,z22,...,zm2},...,max{z1n,z2n,...,zmn})
最小值 ( z 1 − , z 2 − . . . z n − ) = ( min { z 11 , z 21 , . . . , z m 1 } , min { z 12 , z 22 , . . . , z m 2 } , . . . , min { z 1 n , z 2 n , . . . , z m n } ) ∣ 最小值(z^{-}_1,z^{-}_2 ...z^{-}_n) = \left.\left(\min\begin{Bmatrix}z_{11},z_{21},...,z_{m1}\end{Bmatrix},\min\begin{Bmatrix}z_{12},z_{22},...,z_{m2}\end{Bmatrix},...,\min\begin{Bmatrix}z_{1n},z_{2n},...,z_{mn}\end{Bmatrix}\right)\right| 最小值(z1−,z2−...zn−)=(min{z11,z21,...,zm1},min{z12,z22,...,zm2},...,min{z1n,z2n,...,zmn})
D i + = ∑ j = 1 m ( z j + − z i j ) 2 D_{i}^{+}=\sqrt{\sum_{j=1}^{m}(z_{j}^{+}-z_{ij})^{2}} Di+=j=1∑m(zj+−zij)2
D i − = ∑ j = 1 m ( z j − − z i j ) 2 {\cal D}_{i}^{-}=\sqrt{\sum_{j=1}^{m}(z_{j}^{-}-z_{ij})^{2}} Di−=j=1∑m(zj−−zij)2
- 计算出第 i i i 个评价对象未归一化后的得分: S i S_i Si ,很明显 0 < = S i < = 1 0<= S_i <=1 0<=Si<=1,且 S i S_i Si 越大 D i + D^{+}_i Di+ 越小,越接近最大值。
S i = D i − D i + + D i − S_i=\frac{D_i^-}{D_i^++D_i^-} Si=Di++Di−Di−
- 计算归一化后的得分:即每分数除以所有分数之和:
s t a n d _ S = S i ∑ i = 1 n S i stand\_S=\frac{S_i}{\sum_{i=1}^nS_i} stand_S=∑i=1nSiSi
程序代码
function [score]=mfunc_TOPSIS(data,W) % TOPSIS方法:求解每个对象的综合评价得分% paramts: % data: 原始数据矩阵,(m,n) m为评价对象,n为评价指标% W: 每个指标的初始权重% returns:% Score:每个评价对象的综合得分%X输入的数据,W各指标的权重[n,~]=size(data);%Z=zscore(X);Z = data ./ repmat(sum(data.*data) .^ 0.5, n, 1); %矩阵标准化V_D = sum(((Z - repmat(max(Z),n,1)) .^ 2 ) .* repmat(W,n,1) ,2) .^ 0.5; V_X = sum(((Z - repmat(min(Z),n,1)) .^ 2 ) .* repmat(W,n,1) ,2) .^ 0.5; S = V_X ./ (V_D+V_X); %未归一化得分Score_S = S / sum(S); %归一化得分,即为每个企业的投资风险评分,值越大,投资风险也越大% score=Score_S;score=100*Score_S/max(Score_S);
end
相关文章:

数学建模:TOPSIS分析
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 TOPSIS分析法 算法流程 假设有m个评价对象,n个评价指标,首先需要进行指标的正向化: 极大型极小型单点型区间型 然后对正向化后的矩阵进行标准化,得到 Z Z Z…...

【Qt学习】10 利用QSharedMemory实现单例运行
问题 让应用程序只有一个运行实例 QSharedMemory除了可以完成进程间通信,还可以实现应用程序单例化。 解法 首先,看看QSharedMemory的几个函数: 1、QSharedMemory(const QString &key, QObject *parent Q_NULLPTR)构造函数 该构造函数…...

FPGA应用于图像处理
FPGA应用于图像处理 FPGA(Field-Programmable Gate Array)直译过来就是现场可编程门阵列。是一种可以编程的逻辑器件,具有高度的灵活性,可以根据具体需求就像编程来实现不同的功能。 FPGA器件属于专用的集成电流中的一种半定制电…...

vscode python 无法引入上层目录解决
在vscode 中.vscode 配置如下 { // Use IntelliSense to learn about possible attributes. // Hover to view descriptions of existing attributes. // For more information, visit: https://go.microsoft.com/fwlink/?linkid830387 “version”: “0.2.0”, “configurati…...

[开发|java] java list 取某个属性最大的项
示例代码: import java.util.*;class Person {private String name;private int age;public Person(String name, int age) {this.name name;this.age age;}public int getAge() {return age;} }public class Main {public static void main(String[] args) {List<Person…...

关闭浏览器的跨域校验
首发博客地址 问题描述 当你访问资源失败,并遇到以下类似提示时: Access to script at 资源路径 from origin null has been blocked by CORS policy: Cross origin requests are only supported for protocol schemes: http, data, isolated-app, chrom…...
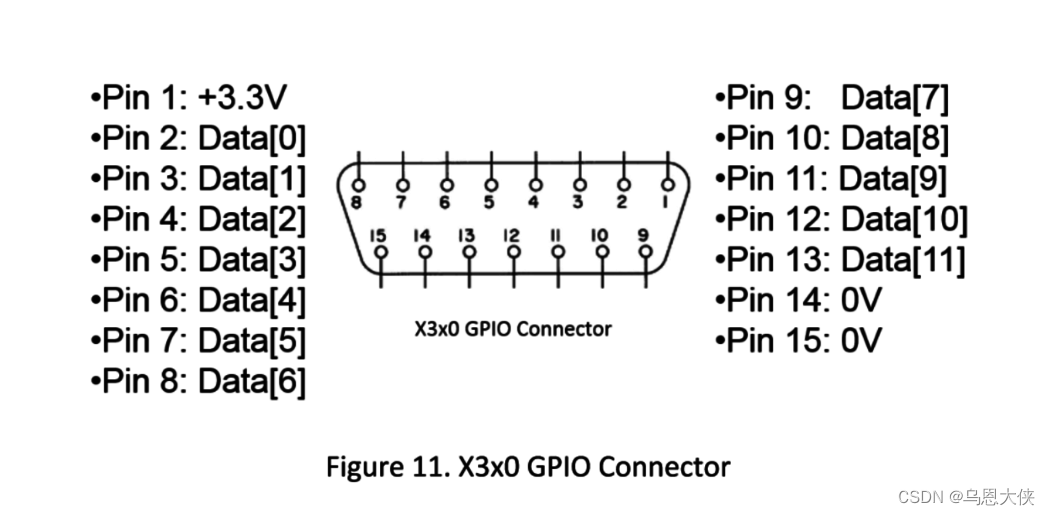
USRP 简介,对于NI软件无线电你所需要了解的一切
什么是 USRP 通用软件无线电外设( USRP ) 是由 Ettus Research 及其母公司National Instruments设计和销售的一系列软件定义无线电。USRP 产品系列由Matt Ettus领导的团队开发,被研究实验室、大学和业余爱好者广泛使用。 大多数 USRP 通过以太网线连接到主机&…...

RTE_Driver驱动框架和Keil下开发需要支持的xxx_DFP软件包分析
1.RTE_Driver驱动框架 RTE_Driver代表"Run-Time Environment Driver",是Keil MDK(Microcontroller Development Kit)中的一个概念。Keil MDK是一种用于嵌入式系统开发的集成开发环境,提供了开发、编译、调试等一系列工具…...

ImportError: Cannot load dynamic library. Did you compile LSD?
1、问题描述 >>> import pylsd2 Traceback (most recent call last):File "<stdin>", line 1, in <module>File "/data/data/wangzy-p-wangzy-p3-volume-pvc-0fee40a7-7013-49b4-8cfb-b4ab0394165b/.conda/envs/paddle/lib/python3.8/sit…...

音频应用编程
目录 ALSA 概述alsa-lib 简介sound 设备节点alsa-lib 移植编写一个简单地alsa-lib 应用程序一些基本概念打开PCM 设备设置硬件参数读/写数据示例代码之PCM 播放示例代码值PCM 录音 使用异步方式PCM 播放示例-异步方式PCM 录音示例-异步方式 使用poll()函数使用poll I/O 多路复用…...
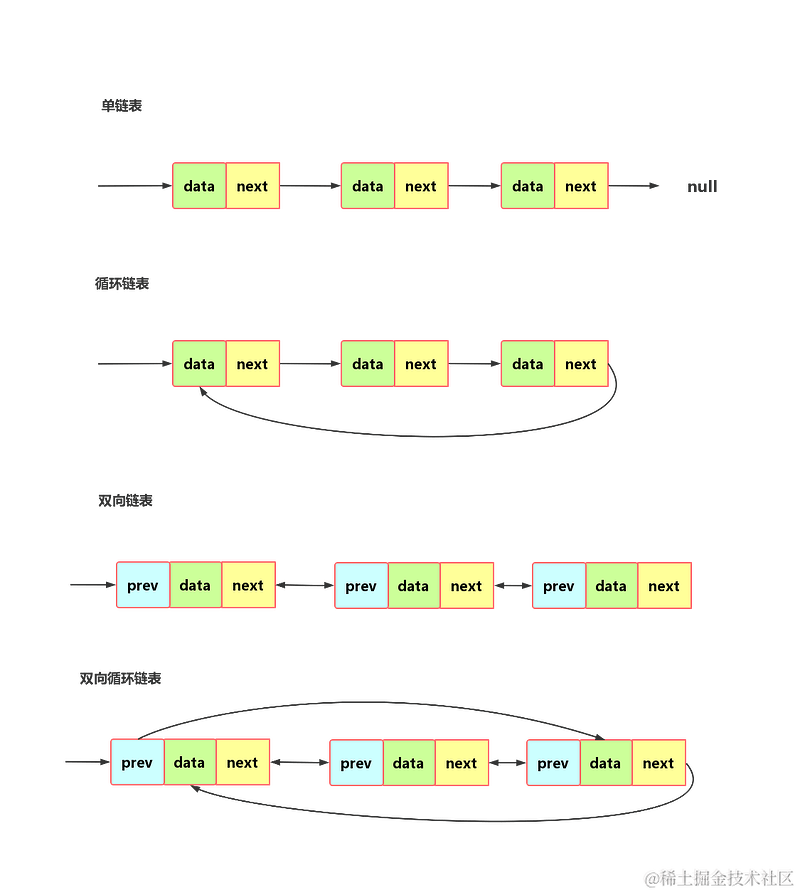
软件测试/测试开发丨Python 学习笔记 之 链表
点此获取更多相关资料 本文为霍格沃兹测试开发学社学员学习笔记分享 原文链接:https://ceshiren.com/t/topic/26458 链表与数组的区别 复杂度分析 时间复杂度数组链表插入删除O(n)O(1)随机访问O(1)O(n) 其他角度分析 内存连续,利用CPU的机制࿰…...
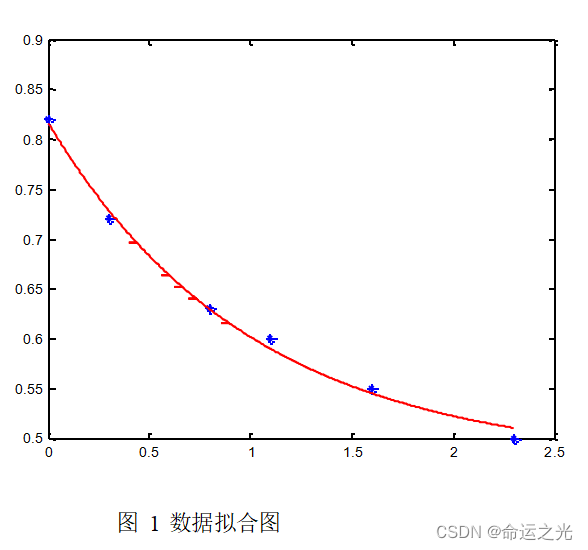
Matlab 使用经验分享(常用函数介绍;矩阵常见计算)
Matlab 使用经验分享 大家好!最近有很多朋友询问我关于 Matlab 的使用,于是我决定写一篇博客来分享一下我的经验。对于数学和编程爱好者来说,Matlab 是一个非常有用的工具。我自己在数学实验和数学建模竞赛中也经常使用它。那么,…...

软件工程(十七) 行为型设计模式(三)
1、观察者模式 简要说明 定义对象间的一种一对多的依赖关系,当一个对象的状态发生改变时,所有依赖于它的对象都得到通知并自动更新 速记关键字 联动,广播消息 类图如下 基于上面的类图,我们来实现一个监听器。类图中的Subject对应我们的被观察对象接口(IObservable),…...
在抖音中使用语聚AI,实现自动回复用户视频评论、私信问答
您可以通过集简云数据流程,将语聚AI助手集成到抖音视频评论、抖音私信,实现自动回复用户视频评论、私信问答,大大提升账号互动与运营效率。 效果如下: 自动化流程: ● 抖音普通号评论对接语聚AI(点击可一…...

pyqt5-快捷键QShortcut
import sys from PyQt5.QtWidgets import * from PyQt5.QtCore import * from PyQt5.QtGui import *""" 下面示例揭示了,当关键字绑定的控件出现的时候,快捷键才管用, 绑定的控件没有出现的时候快捷键无效 """…...
匿名函数( lambda 表达式)
在 C 中,匿名函数也被称为 lambda 表达式。C11 引入了 lambda 表达式,使得在需要函数对象(函数符)的地方可以使用匿名函数来代替。 lambda 表达式的基本语法如下: [capture list] (parameter list) -> return typ…...

基于SSM的汽车维修管理系统——LW模板
摘要 随着人们生活水平的不断提高,私家车的数量正在逐年攀升。这带动了汽车维修行业的发展。越来越多的汽车维修厂如雨后春笋般涌现。同时,维修厂的业务操作产生了庞大的数据,这给汽车维修厂工作人员的数据管理提出了新的要求,他们…...
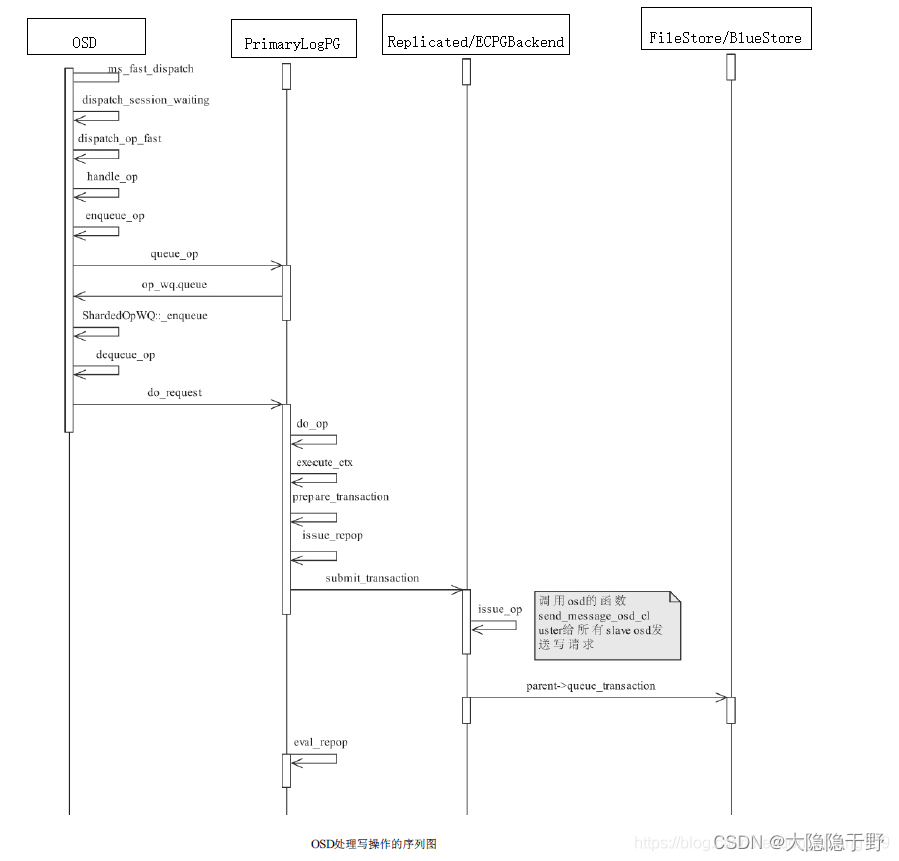
Ceph的纠删码特性 EC(Erasure Code)代码流程
从GitHub上Clone Ceph项目,我是基于(ceph version 12.2.11 luminous 版本)的代码来分析的 一、EC(Erasure Code)是什么? Ceph的纠删码特性EC:将写入的数据分成N份原始数据,通过这N份原始数据计算出M份效验…...

盘点那些国际知名黑客(上篇)
电影中的黑客仅靠一部电脑就可以窃取别人的信息,利用自己高超的技术让公司甚至国家都胆战心惊。“黑客”原指热心于计算机技术、水平高超的电脑高手,但逐渐区分为黑帽、白帽、灰帽。这些术语源自美国流行文化的老式西部电影,其中主角戴白色或…...
)
机器学习基础12-Pipeline实现自动化流程处理(基于印第安糖尿病Pima 数据集)
有一些标准的流程可以实现对机器学习问题的自动化处理,在 scikitlearn 中通过Pipeline来定义和自动化运行这些流程。本节就将介绍如何通过Pipeline实现自动化流程处理。 如何通过Pipeline来最小化数据缺失。如何构建数据准备和生成模型的Pipeline。如何构建特征选择…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
