Matlab 使用经验分享(常用函数介绍;矩阵常见计算)
Matlab 使用经验分享
大家好!最近有很多朋友询问我关于 Matlab 的使用,于是我决定写一篇博客来分享一下我的经验。对于数学和编程爱好者来说,Matlab 是一个非常有用的工具。我自己在数学实验和数学建模竞赛中也经常使用它。那么,为什么 Matlab 这么受欢迎呢?
Matlab 的起源
MATLAB 是美国MathWorks 公司自20 世纪 80 年代中期推出的数学软件, 优秀的数值 计算能力和卓越的数据可视化能力使其很快在数学软件中脱颖而出。
为什么选择 Matlab?
由于 Maltab 编程方便,有大量内部函数和工具箱可以使用,作图也十分方便,因此在 数学实验和数学建模竞赛中,我们就常使用 Matlab 作为我们的编程工具。
一些常用函数介绍
- 三角函数
- sin: --正弦
- sinh: 双曲正弦
- asin: -反正弦
- cosh: 双曲余弦
- acos: -反余弦
- atanh: --反双曲正切
- 指数函数与对数函数
- exp: -指数
- log: --e 为底的对数
- log10: 常用对数
- sqrt: --平方根
- 与复数有关的函数
- abs: -模或绝对值
- angle: 幅角
- conj: 复共轭
- imag: 虚部
- real: --实部
- 舍入函数及其它数值函数
- fix: – 向 0 舍入
- floor: 向负无穷舍入
- ceil: – 向正无穷舍入
- sign(x): -符号函数
- min(x): 向量 x 的元素的最小值
- max(x): 向量 x 的元素的最大值
- mean(x): 向量 x 的元素的平均值
- median(x): 向量 x 的元素的中位数
- std(x): 向量 x 的元素的标准差
- diff(x): 向量 x 的相邻元素的差
- sort(x): 对向量 x 的元素进行排序
- length(x): 向量 x 的元素个数
- norm(x): 向量 x 的 Euclidean 长度
- sum(x): 向量 x 的元素总和
- prod(x): 向量 x 的元素连乘积
- cumsum(x): 向量 x 的累计元素总和
矩阵常见计算
矩阵输入
矩阵输入最简单的方法是把矩阵的元素直接排列在方括号中。每行内的元素间用空格或逗号隔开,行与行之间用分号隔开。例如:
A=[1,4,7;3,6,9;6,7,4]
矩阵的转置
矩阵的转置用符号´来表示。例如:
A=[1,4,7;3,6,9;6,7,4];
B=A´
矩阵的加减
矩阵的加减使用的是”+”和”-“运算符。进行矩阵加减运算必须是同型矩阵。例如:
A=[1,3,6;4,5,7;7,8,9];
B=[3,5,7;2,4,6;1,3,9];
C=A+B
以下是关于矩阵与标量进行加减运算的内容:
矩阵可以与一个数进行加减运算,运算法则是对应每个元素加减同一个数。例如:
Z=C-1
结果为:
Z =
3
5
…
矩阵乘法
矩阵乘法用符号*表示。要求前一矩阵的列数与后一矩阵的行数相同。例如:
A=[1,4,7;2,5,8];
B=[4,5,9;1,7,8;3,2,1];
C=A*B
在 Matlab 中,还可以进行矩阵与数的乘法。其规则是矩阵的每个元素与该数相乘。例如:
A=[1,5,8;2,6,9];
B=3*A
结果为:
B =
3 15 24
6 18 27
矩阵的行列式
求方阵 A 的行列式,用 det(A) 表示。例如:
A=[1,3,6;2,5,8;3,9,11];
Z=det(A)
矩阵求逆
非奇异矩阵 ( A ) 的求逆用 inv(A) 表示。例如:
A=[1,3,6;2,5,8;3,9,11];
Z=inv(A)
结果为:
Z =
-2.4286 3.0000 -0.8571
0.2857 -1.0000 0.5714
…
以下是关于如何验证矩阵的逆以及如何使用逆矩阵来解方程组的内容:
要验证矩阵的逆是否正确,可以计算 ( C = A \times Z )。例如:
C =1.0000 0 -0.00000 1.0000 -0.0000...
利用逆矩阵可以解方程组。例如:
AX=b
其中:
A=[1,3,6;…
以下是关于如何使用矩阵来解方程组和函数拟合的内容:
例如,给定以下方程组:
A=[1,3,6;2,5,8;3,9,11];
b=[3,6,7]';
X=inv(A)*b
结果为:
X =
4.7143
-1.1429
0.2857
或者,使用 X=A\b 也可以求解。此外,X=A\b 还可以求解矛盾方程组。
函数拟合
假设因变量 y 与自变量 x 之间存在以下关系:
y = a + b * exp(-x)
观测数据为:
| x | 0.0 | 0.3 | 0.8 | 1.1 | 1.6 | 2.3 |
| y | 0.82| 0.72| 0.63| 0.60| 0.55| 0.5 |
基于这些数据,我们可以建立矛盾方程组 AX=y,其中X=[a,b] ′
以下是关于如何使用 m 文件进行函数拟合的内容:
我们可以创建以下 m 文件来进行拟合:
t=[0.0, 0.3, 0.8, 1.1, 1.6, 2.3]‘;
y=[0.82, 0.72, 0.63, 0.60, 0.55, 0.5]’;
A=[ones(size(t)),exp(-t)];
X=inv(A’*A)*A’*y;
或者
X=A\y;
计算结果为:
X = 0.4760 0.3413
即:a=0.4760,b=0.3413。
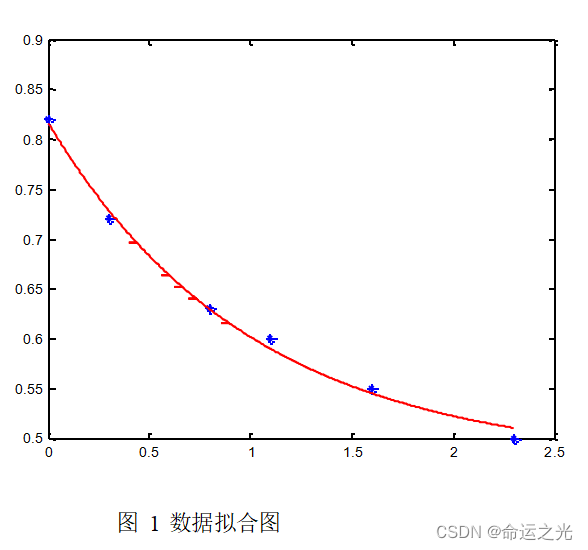
函数拟合为:y=0.476+0.3413×e^x 。
我们可以使用图形来表示结果。
以下是 M 文件的内容:
M 文件如下
t=[0.0 0.3 0.8 1.1 1.6 2.3]’
y=[0.82 0.72 0.63 0.60 0.55 0.5]’
A=[ones(size(t)),exp(-t)]
x=inv(A’*A)*A’y
n=500
tt=zeros(n,1);
yy=zeros(n,1);
dt=2.3/n;
for i=1:n
tt(i)=idt;
yy(i)=x(1)+x(2)*exp(-tt(i));
end
plot(t,y,‘*b’,tt,yy,‘r’)
b—表示蓝色,代表原数据
r-----表示红色,代表拟合曲线
矩阵特征值
如果 A 为方阵,满足 AX=λX 的 λ 称为 A 的特征值,X 称为 A 的特征向量。计算 A 的特征值用 eig(A)表示。
例如:
A=[1 3 6; 2 5 8; 3 6 8];
Z=eig(A)
结果为:
Z =
15.2382
-1.3365
0.0982
如要同时求出特征向量,采用表达式 [X,V]=eig(A)。
结果为:
X = -0.4135 -0.6094
-0.6765
V =
15.2382
0
0
需要直接看PDF文件,直接在博主主页的资源里免费下载,因为博主写的时候可能个别的会有缺漏,需要看原文档的直接下载即可。
相关文章:

Matlab 使用经验分享(常用函数介绍;矩阵常见计算)
Matlab 使用经验分享 大家好!最近有很多朋友询问我关于 Matlab 的使用,于是我决定写一篇博客来分享一下我的经验。对于数学和编程爱好者来说,Matlab 是一个非常有用的工具。我自己在数学实验和数学建模竞赛中也经常使用它。那么,…...

软件工程(十七) 行为型设计模式(三)
1、观察者模式 简要说明 定义对象间的一种一对多的依赖关系,当一个对象的状态发生改变时,所有依赖于它的对象都得到通知并自动更新 速记关键字 联动,广播消息 类图如下 基于上面的类图,我们来实现一个监听器。类图中的Subject对应我们的被观察对象接口(IObservable),…...
在抖音中使用语聚AI,实现自动回复用户视频评论、私信问答
您可以通过集简云数据流程,将语聚AI助手集成到抖音视频评论、抖音私信,实现自动回复用户视频评论、私信问答,大大提升账号互动与运营效率。 效果如下: 自动化流程: ● 抖音普通号评论对接语聚AI(点击可一…...

pyqt5-快捷键QShortcut
import sys from PyQt5.QtWidgets import * from PyQt5.QtCore import * from PyQt5.QtGui import *""" 下面示例揭示了,当关键字绑定的控件出现的时候,快捷键才管用, 绑定的控件没有出现的时候快捷键无效 """…...
匿名函数( lambda 表达式)
在 C 中,匿名函数也被称为 lambda 表达式。C11 引入了 lambda 表达式,使得在需要函数对象(函数符)的地方可以使用匿名函数来代替。 lambda 表达式的基本语法如下: [capture list] (parameter list) -> return typ…...

基于SSM的汽车维修管理系统——LW模板
摘要 随着人们生活水平的不断提高,私家车的数量正在逐年攀升。这带动了汽车维修行业的发展。越来越多的汽车维修厂如雨后春笋般涌现。同时,维修厂的业务操作产生了庞大的数据,这给汽车维修厂工作人员的数据管理提出了新的要求,他们…...
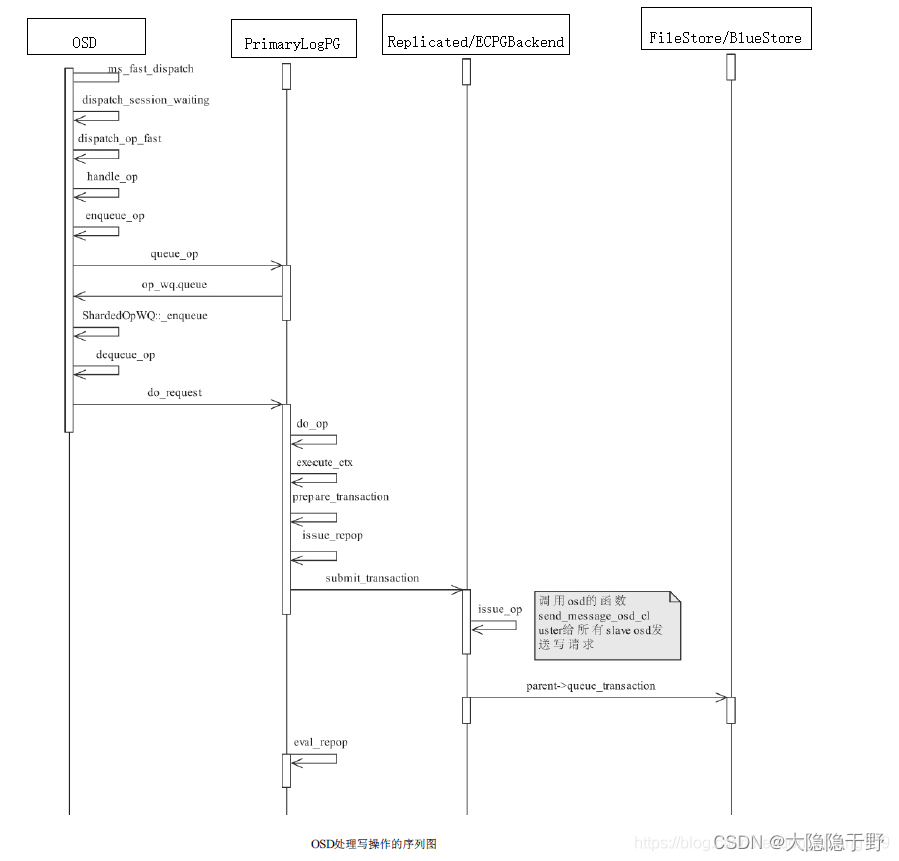
Ceph的纠删码特性 EC(Erasure Code)代码流程
从GitHub上Clone Ceph项目,我是基于(ceph version 12.2.11 luminous 版本)的代码来分析的 一、EC(Erasure Code)是什么? Ceph的纠删码特性EC:将写入的数据分成N份原始数据,通过这N份原始数据计算出M份效验…...

盘点那些国际知名黑客(上篇)
电影中的黑客仅靠一部电脑就可以窃取别人的信息,利用自己高超的技术让公司甚至国家都胆战心惊。“黑客”原指热心于计算机技术、水平高超的电脑高手,但逐渐区分为黑帽、白帽、灰帽。这些术语源自美国流行文化的老式西部电影,其中主角戴白色或…...
)
机器学习基础12-Pipeline实现自动化流程处理(基于印第安糖尿病Pima 数据集)
有一些标准的流程可以实现对机器学习问题的自动化处理,在 scikitlearn 中通过Pipeline来定义和自动化运行这些流程。本节就将介绍如何通过Pipeline实现自动化流程处理。 如何通过Pipeline来最小化数据缺失。如何构建数据准备和生成模型的Pipeline。如何构建特征选择…...
Ansible学习笔记15
1、roles:(难点) roles介绍: roles(角色):就是通过分别将variables,tasks及handlers等放置于单独的目录中,并可以便捷地调用他们的一种机制。 假设我们要写一个playbo…...

圆圈加数字的css
方式一 .circle { width: 50px; height: 50px; border-radius: 50%; background-color: #f00; color: #fff; text-align: center; line-height: 50px; } .circle::before { content: attr(data-number); display: block; } <div class"circle" data-number"…...

YOLOV5/YOLOV7/YOLOV8改进:用于低分辨率图像和小物体的新 CNN 模块SPD-Conv
1.该文章属于YOLOV5/YOLOV7/YOLOV8改进专栏,包含大量的改进方式,主要以2023年的最新文章和2022年的文章提出改进方式。 2.提供更加详细的改进方法,如将注意力机制添加到网络的不同位置,便于做实验,也可以当做论文的创新点。 3.涨点效果:SPD-Conv提升小目标识别,实现有效…...
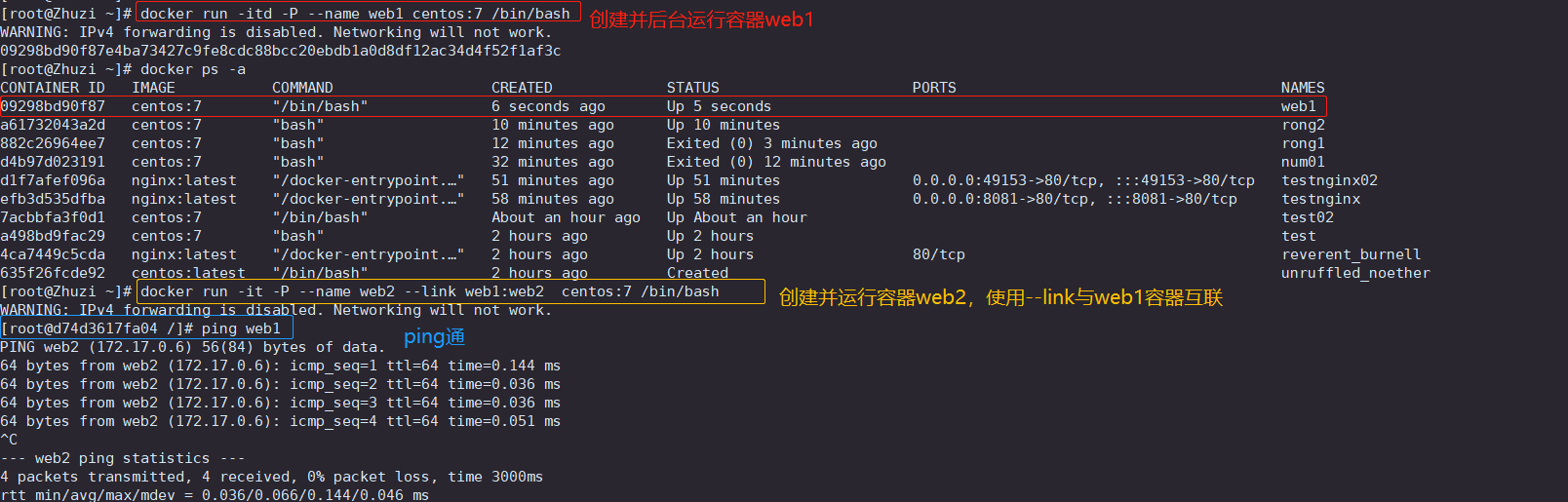
Docker数据管理(数据卷与数据卷容器)
目录 一、数据卷(Data Volumes) 1、概述 2、原理 3、作用 4、示例:宿主机目录 /var/test 挂载同步到容器中的 /data1 二、数据卷容器(DataVolumes Containers) 1、概述 2、作用 3、示例:创建并使用…...

大量TCP连接滞留TIME_WAIT、SYN_SENT、CLOSE_WAIT状态的分析
文章目录 一、统计各类状态的tcp连接数量二、TIME_WAIT应用服务器上,来自反向代理的连接反向代理上,访问应用服务的连接反向代理上,来自用户的连接 三、SYN_SENT反向代理上,访问位于防火墙另一侧的目标反向代理上,访问…...

kotlin怎么定义类
在Kotlin中,你可以使用class关键字来定义一个类。以下是一个简单的例子: class MyClass {// class body} 这个例子定义了一个名为MyClass的类。你可以在类体中定义属性和方法。 如果你想定义一个带有属性的类,你可以这样做: cla…...

如何查看数据集下载后保存的绝对路径?
1.问题 当我们下载torchvision.datasets里面的数据集时,有时候会遇到找不到数据集保存路径的问题。 2.解决 引入os库 import os调用如下方法 os.path.abspath(数据集对象.root)以下面代码为例 import os import torchvision.datasets as datasets# 指定数据集…...
使用php实现微信登录其实并不难,可以简单地分为三步进行
使用php实现微信登录其实并不难,可以简单地分为三步进行。 第一步:用户同意授权,获取code //微信登录public function wxlogin(){$appid "";$secret "";$str"http://***.***.com/getToken";$redirect_uriu…...
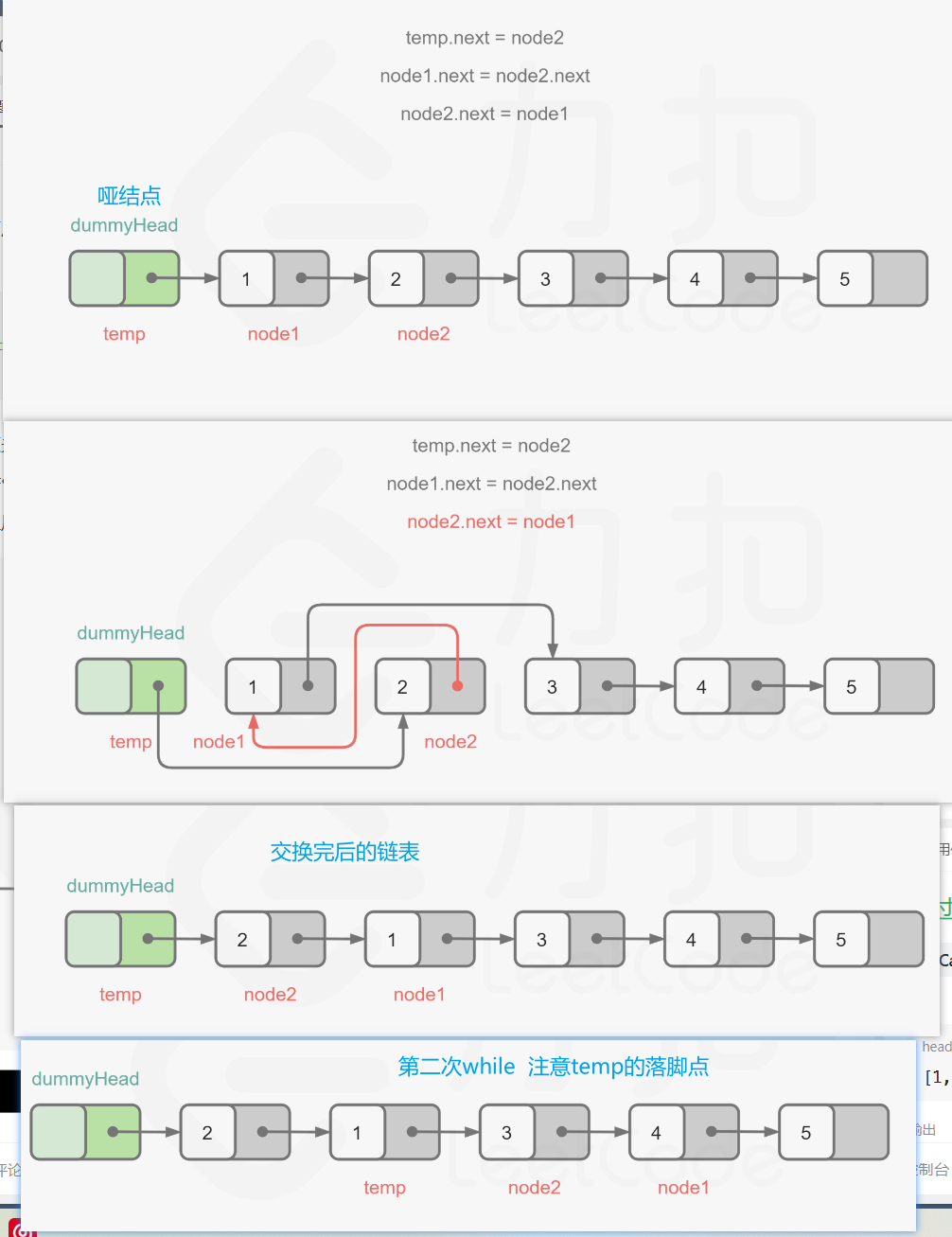
【LeetCode-中等题】24. 两两交换链表中的节点
文章目录 题目方法一:递归方法二:三指针迭代 题目 方法一:递归 图解: 详细版 public ListNode swapPairs(ListNode head) {/*递归法:宗旨就是紧紧抓住原来的函数究竟返回的是什么?作用是什么即可其余的细枝末节不要细究,编译器…...

5.10 汇编语言:汇编过程与结构
过程的实现离不开堆栈的应用,堆栈是一种后进先出(LIFO)的数据结构,最后压入栈的值总是最先被弹出,而新数值在执行压栈时总是被压入到栈的最顶端,栈主要功能是暂时存放数据和地址,通常用来保护断点和现场。 栈是由CPU管…...

【每日一题Day304】LC1267统计参与通信的服务器 | 哈希表
统计参与通信的服务器【LC1267】 这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表示没有。 如果两台服务器位于同一行或者同一列,我们就认为它们之间可以进行通信。 请你统…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
