【每日一题Day304】LC1267统计参与通信的服务器 | 哈希表
统计参与通信的服务器【LC1267】
这里有一幅服务器分布图,服务器的位置标识在
m * n的整数矩阵网格grid中,1 表示单元格上有服务器,0 表示没有。如果两台服务器位于同一行或者同一列,我们就认为它们之间可以进行通信。
请你统计并返回能够与至少一台其他服务器进行通信的服务器的数量。
-
思路
使用哈希表记录能与至少一台其他服务器进行通信的服务器坐标,那么最终结果即为哈希表的大小。
- 首先按行遍历元素,找到能与同行服务器通信的服务器坐标,记录前一个服务器的坐标,如果不为-1,那么将前一个服务器和当前服务器添加至结果集
- 然后按列遍历元素,找到能与同列服务器通信的服务器坐标,流程同上
-
实现
class Solution {public int countServers(int[][] grid) {int m = grid.length, n = grid[0].length;Set<Integer> set = new HashSet<>();for (int i = 0; i < m; i++){int pre = -1;for (int j = 0; j < n; j++){if (grid[i][j] == 1){if (pre != -1){set.add(pre);set.add(i * n + j);}pre = i * n + j;}}}for (int j = 0; j < n; j++){int pre = -1;for (int i = 0; i < m; i++){if (grid[i][j] == 1){if (pre != -1){set.add(pre);set.add(i * n + j);}pre = i * n + j;}}}return set.size();} }- 复杂度
- 时间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)
- 空间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)
- 复杂度
-
实现
先遍历一遍矩阵,统计每行每列的服务器个数;然后再遍历一遍矩阵,如果该行或者该列服务器个数大于1,那么数量+1
class Solution {public int countServers(int[][] grid) {int m = grid.length, n = grid[0].length;int[] row = new int[m];int[] col = new int[n];for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {if (grid[i][j] == 1) {row[i]++;col[j]++;}}}int ans = 0;for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {if (grid[i][j] == 1 && (row[i] > 1 || col[j] > 1)) {++ans;}}}return ans;} }作者:ylb 链接:https://leetcode.cn/problems/count-servers-that-communicate/solutions/2402089/python3javacgotypescript-yi-ti-yi-jie-ji-arec/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。- 复杂度
- 时间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)
- 空间复杂度: O ( n + m ) O(n+m) O(n+m)
- 复杂度
相关文章:

【每日一题Day304】LC1267统计参与通信的服务器 | 哈希表
统计参与通信的服务器【LC1267】 这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表示没有。 如果两台服务器位于同一行或者同一列,我们就认为它们之间可以进行通信。 请你统…...

深度解读零信任身份安全—— 全面身份化:零信任安全的基石
事实上,无论是零信任安全在数据中心的实践,还是通用的零信任安全架构实践,全面身份化都是至关重要的,是“企业边界正在瓦解,基于边界的安全防护体系正在失效”这一大背景下,构筑全新的零信任身份安全架构的…...

音视频 ffmpeg命令提取音视频数据
保留封装格式 ffmpeg -i test.mp4 -acodec copy -vn audio.mp4 ffmpeg -i test.mp4 -vcodec copy -an video.mp4提取视频 保留编码格式:ffmpeg -i test.mp4 -vcodec copy -an test_copy.h264 强制格式:ffmpeg -i test.mp4 -vcodec libx264 -an test.h2…...

vscode 配置
vscode 配置 安装插件 Better C SyntaxC/CCMake、CMake Tools 、CMake Language SupportDoxygen Documentation GeneratorGit Graphhighlight-wordsPythonvscode-iconsClang-Format和clangdtyporahex editor .vscode 中的文件 在 VS Code 中,.vscode 文件夹是用于…...

企业数字化管控平台及信息化治理体系建设方案(附300份方案)
本资料来源公开网络,仅供个人学习,请勿商用,如有侵权请联系删除,更多浏览公众号:智慧方案文库 数字化校园整体解决方案.doc150页6万字数字化智能工厂信息化系统集成整合规划建设方案.docx2022年采购数字化市场研究报告…...

ABB PCD231B通信输入/输出模块
多通道输入和输出: PCD231B 模块通常配备多个输入通道和输出通道,用于连接传感器、执行器和其他设备。 通信接口: 这种模块通常支持各种通信接口,如以太网、串口(RS-232、RS-485)、Profibus、CAN 等&#…...
在springboot项目中显示Services面板的方法
文章目录 前言方法一:Alt8快捷键方法二:使用Component标签总结 前言 在一个springboot项目中,通过开启Services面板,可以快速的启动、配置、管理多个子项目。 方法一:Alt8快捷键 1、在idea界面输入Alt8,在…...

spring之AOP简介
1.AOP简介 什么是AOP Aspect Oriented Program面向切面编程在不改变原有逻辑上增加额外的功能,比如解决系统层面的问题,或者增加新的功能 场景 权限控制缓存日志处理事务控制 AOP思想把功能分两个部分,分离系统中的各种关注点 核心关注点&a…...

ros::init用途用法
文章目录 用途:用法:ros::init 是 ROS(Robot Operating System)中的一个重要函数,它用于初始化 ROS 节点。在启动任何 ROS 节点之前,都必须首先调用这个函数。以下是其用途和基本用法。 用途: 节点初始化:为ROS系统中的节点进行初始化。一个节点是ROS计算图中的一个可…...

逻辑回归的含义
参考:线性回归 & 逻辑回归 问题 1、线性回归(Linear Regression)和逻辑回归(Logistic Regression)有什么联系? 2、逻辑回归的“逻辑”、“回归是什么意思”? 回答1 线性回归假设因变量…...

解决Apache Tomcat “Request header is too large“ 异常
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
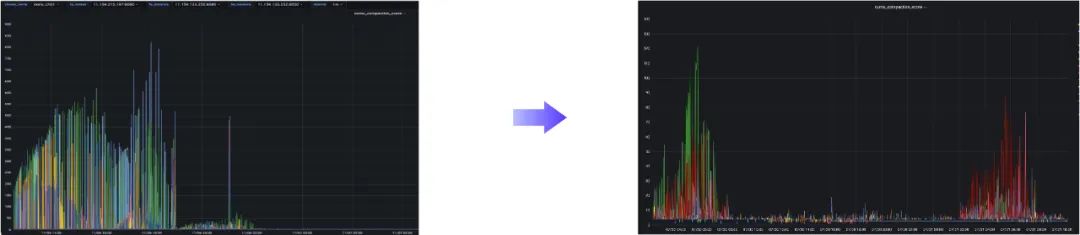
腾讯音乐如何基于大模型 + OLAP 构建智能数据服务平台
本文导读: 当前,大语言模型的应用正在全球范围内引发新一轮的技术革命与商业浪潮。腾讯音乐作为中国领先在线音乐娱乐平台,利用庞大用户群与多元场景的优势,持续探索大模型赛道的多元应用。本文将详细介绍腾讯音乐如何基于 Apach…...
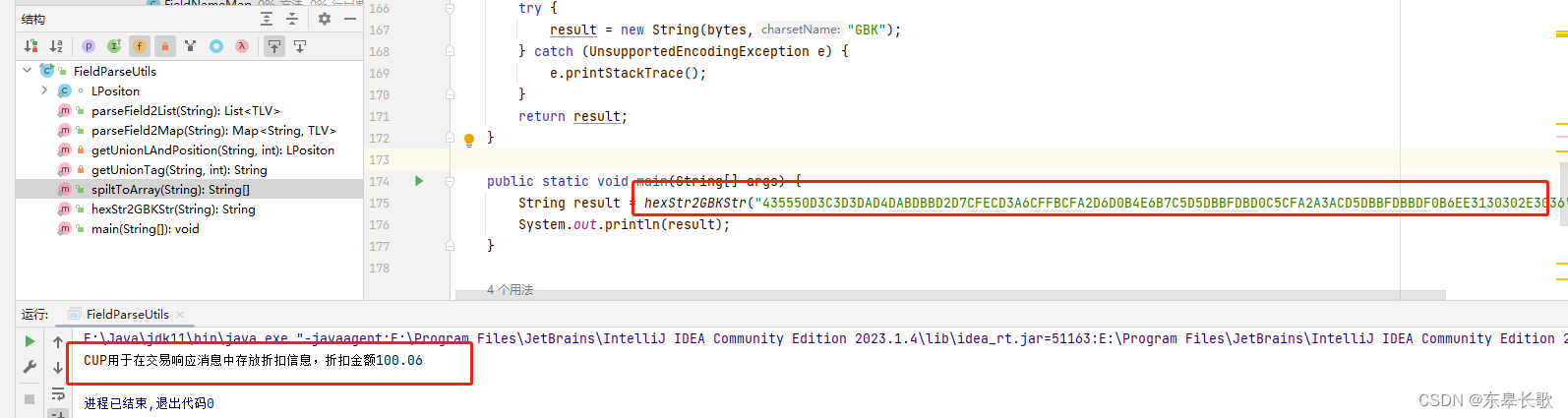
Java 16进制字符串转换成GBK字符串
问题: 现在已知有一个16进制字符串 435550D3C3D3DAD4DABDBBD2D7CFECD3A6CFFBCFA2D6D0B4E6B7C5D5DBBFDBD0C5CFA2A3ACD5DBBFDBBDF0B6EE3130302E3036 而且知道这串的字符串对应的内容是: CUP用于在交易响应消息中存放折扣信息,折扣金额100.06 但…...

【ES6】JavaScript中的Symbol
Symbol是JavaScript中的一种特殊的、不可变的、不可枚举的数据类型。它通常用于表示一个唯一的标识符,可以作为对象的属性键,确保对象的属性键的唯一性和不可变性。 Symbol.for()是Symbol的一个方法,它用于创建一个已经注册的Symbol对象。当…...

理解React页面渲染原理,如何优化React性能?
React JSX转换成真实DOM过程 当使用React编写应用程序时,可以使用JSX语法来描述用户界面的结构。JSX是一种类似于HTML的语法,但实际上它是一种JavaScript的扩展,用于定义React元素。React元素描述了我们想要在界面上看到的内容和结构。 在运…...
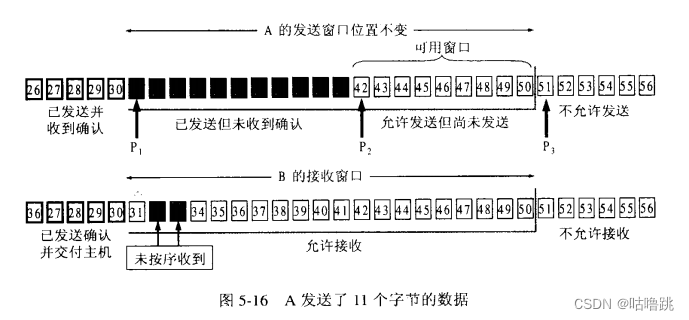
数据通信——传输层TCP(可靠传输机制的滑动窗口)
引言 之前提到过拥塞问题,如果大量数据疯狂涌入,接收端无法及时处理就会导致数据丢包,从而使得通信受到干扰。之前的连续ARQ如果不加以节制,疯狂发送报文,接收端无法及时返回ACK就会导致网络瘫痪。 滑动窗口机制协议 这…...
Mycat之前世今生
如果我有一个32核心的服务器,我就可以实现1个亿的数据分片,我有32核心的服务器么?没有,所以我至今无法实现1个亿的数据分片。——MyCAT ‘s Plan 话说“每一个成功的男人背后都有一个女人”,自然MyCAT也逃脱不了这个诅…...
和标准错误(stderr))
Linux- 重定向标准输出(stdout)和标准错误(stderr)
在Linux或Unix系统中,可以通过重定向标准输出(stdout)和标准错误(stderr)来将脚本的输出保存到一个文件中。以下是一些方法: 只重定向标准输出到文件: ./your_script.sh > output.txt这将只捕…...
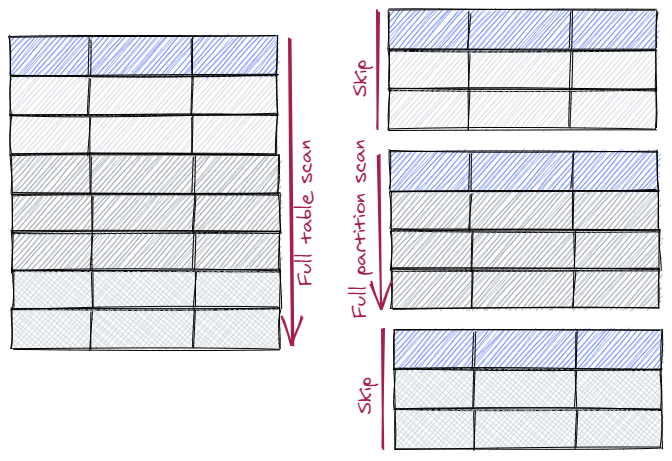
PostgreSQL分区表
什么是分区表 数据库分区表将表数据分成更小的物理分片,以此提高性能、可用性、易管理性。分区表是关系型数据库中比较常见的对大表的优化方式,数据库管理系统一般都提供了分区管理,而业务可以直接访问分区表而不需要调整业务架构,…...
)
android framework之Applicataion启动流程分析(二)
上一篇讲了Zygote是如何收到启动Application的启动消息,并一步步进入Fork(),下面来分析zygote fork启动application后,application进程后续处理操作,是如何真正的启动的。 ZygoteInit.main():-->...caller ZygoteServer.runSelectLoop()…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
