机器学习简介[01/2]:简单线性回归
Python 中的机器学习简介:简单线性回归
一、说明
二、技术背景
这是涵盖回归、梯度下降、分类和机器学习的其他基本方面的系列文章的第一篇文章。本文重点介绍简单的线性回归,它确定了一组点的最佳拟合线,以便进行将来的预测。
2.1 最佳拟合线

最佳拟合线是最准确地表示一组点的方程。对于给定的输入,公式的输出应尽可能接近预期输出。
在上图中,很明显,中间线比左线或右线更适合蓝点。但是,它是最适合的路线吗?有没有第四条线更适合这些观点?这条线当然可以向上或向下移动,以确保相同数量的点落在其上方和下方。但是,可能有十几行符合此确切标准。是什么让其中任何一个成为最好的?
值得庆幸的是,有一种方法可以使用回归在数学上确定一组点的最佳拟合线。
2.2 回归
回归有助于识别两个或多个变量之间的关系,它采用多种形式,包括简单线性、多重线性、多项式等。为了证明这种方法的有用性,将使用简单的线性回归。
简单线性回归尝试找到一组点的最佳拟合线。更具体地说,它标识自变量和因变量之间的关系。最佳拟合线的形式为 y = mx + b。
- x 是输入或自变量
- m 是直线的斜率或陡度
- b 是 y 截距
- y 是输出或因变量
简单线性回归的目标是确定 m 和 b 的值,当给定 x 时,这些值将生成最准确的 y 值。这个方程,也称为模型,也可以用机器学习术语进行评估。在等式中,w 表示“重量”:Ŷ = Xw₁+ w₀
- X 是输入或特征
- w₁ 是斜率
- w₀ 是偏置或 y 截距
- Ŷ 是预测,发音为“y-hat”
虽然这很有用,但需要评估方程的准确性。如果它的预测很差,它就不是很有用。为此,使用成本或损失函数。
2.3 成本或损失函数
回归需要某种方法来跟踪模型预测的准确性。给定输入,方程的输出是否尽可能接近预期输出?成本函数,也称为损失函数,用于确定方程的精度。
例如,如果预期输出为 5,而方程输出为 18,则损失函数应表示此差值。一个简单的损失函数可以输出 13,这是这些值之间的差值。这表明模型的性能很差。另一方面,如果预期输出为 5,模型预测为 5,则损失函数应输出 0,这表明模型的性能非常出色。
执行此操作的常用损失函数是均方误差 (MSE):
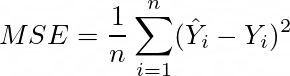
此函数用于查找模型的预测 (Ŷ) 和预期输出 (Y) 之间的差异。然后对差值进行平方,以确保输出始终为正。它跨一组大小为 n 的点执行此操作。通过将所有这些点的平方差相加并除以 n,输出是均方差(误差)。这是一种同时评估模型在所有点上的性能的简单方法。下面可以看到一个简单的例子:
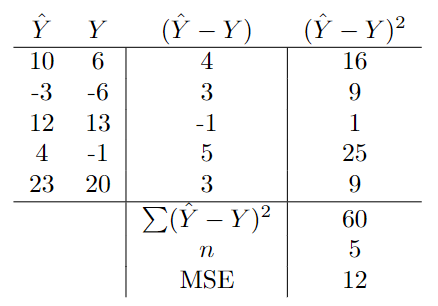
虽然还有无数其他损失函数同样适用于这种情况,但由于其简单性,这是机器学习中回归中最受欢迎的损失函数之一,尤其是在梯度下降方面,这将在后面解释。
为了最好地理解梯度下降的位置,可以评估一个示例。
三、预测最佳拟合线
若要显示操作中的简单线性回归,需要数据来训练模型。这以 X 数组和 Y 数组的形式出现。对于此示例,可以手动生成数据。它可以从“蓝图”函数创建。随机性可以添加到蓝图中,模型将被强制学习底层函数。PyTorch,一个标准的机器学习库,用于实现回归。
3.1 生成数据
首先,下面的代码使用随机整数生成器生成一个输入值数组。X 当前具有 (n 个样本,num 特征)的形状。请记住,特征是一个自变量,简单线性回归有 1。在本例中,n 将为 20。
import torchtorch.manual_seed(5)
torch.set_printoptions(precision=2)# (n samples, features)
X = torch.randint(low=0, high=11, size=(20, 1)) tensor([[ 9],[10],[ 0],[ 3],[ 8],[ 8],[ 0],[ 4],[ 1],[ 0],[ 7],[ 9],[ 3],[ 7],[ 9],[ 7],[ 3],[10],[10],[ 4]])然后可以通过 Y = 1.5X + 2 传递这些值以生成输出值,并且可以使用平均值为 0 且标准差为 1 的正态分布将这些值添加一些随机性。Y 的形状为 (n 个样本,1)。
下面的代码显示了具有相同形状的随机值。
torch.manual_seed(5)# normal distribution with a mean of 0 and std of 1
normal = torch.distributions.Normal(loc=0, scale=1)normal.sample(X.shape)tensor([[ 1.84],[ 0.52],[-1.71],[-1.70],[-0.13],[-0.60],[ 0.14],[-0.15],[ 2.61],[-0.43],[ 0.35],[-0.06],[ 1.48],[ 0.49],[ 0.25],[ 1.75],[ 0.74],[ 0.03],[-1.17],[-1.51]])最后,可以使用下面的代码计算Y。
Y = (1.5*X + 2) + normal.sample(X.shape)Ytensor([[15.00],[15.00],[-0.36],[ 6.75],[13.59],[15.16],[ 2.33],[ 8.72],[ 2.67],[ 1.81],[13.74],[14.06],[ 7.15],[12.81],[15.91],[13.15],[ 6.76],[18.05],[18.71],[ 6.80]])它们也可以与 matplotlib 一起绘制,以便更好地理解它们的关系:
import matplotlib.pyplot as pltplt.scatter(X,Y)
plt.xlim(-1,11)
plt.ylim(0,20)
plt.xlabel("$X$")
plt.ylabel("$Y$")
plt.show()
虽然为示例生成数据似乎违反直觉,但它是演示回归如何工作的好方法。该模型(如下所示)将仅提供 X 和 Y,并且需要将 w₁ 标识为 1.5,将 w₀ 标识为 2。
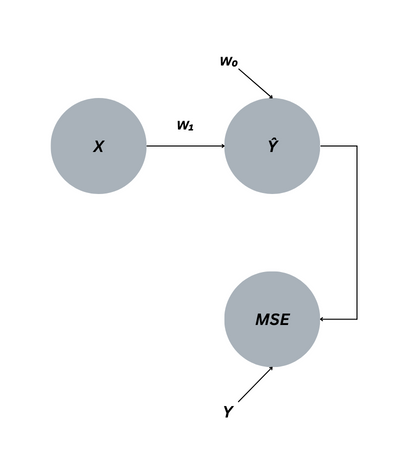
权重可以存储在数组 w 中。 这个数组中有两个权重,一个用于偏差,一个用于特征的数量。它的形状为 (数字特征 + 1 个偏差,1)。对于此示例,数组的形状为 (2, 1)。
torch.manual_seed(5)
w = torch.rand(size=(2, 1))
w tensor([[0.83],[0.13]])生成这些值后,可以创建模型。
3.2 创建模型
模型的第一步是为最佳拟合线定义一个函数,为 MSE 定义另一个函数。
如前所述,该模型的方程为 Ŷ = Xw₁+ w₀。 截至目前,偏差已添加到每个样本中。这相当于将偏差广播为与 X 大小相同并将数组相加。输出如下所示。
w[1]*X + w[0]tensor([[1.97],[2.09],[0.83],[1.21],[1.84],[1.84],[0.83],[1.33],[0.96],[0.83],[1.71],[1.97],[1.21],[1.71],[1.97],[1.71],[1.21],[2.09],[2.09],[1.33]])下面的函数计算输出。
# line of best fit
def model(w, X):"""Inputs:w: array of weights | (num features + 1 bias, 1)X: array of inputs | (n samples, num features + 1 bias)Output:returns the predictions | (n samples, 1)"""return w[1]*X + w[0]MSE 的功能非常简单:
# mean squared error (MSE)
def MSE(Yhat, Y):"""Inputs:Yhat: array of predictions | (n samples, 1)Y: array of expected outputs | (n samples, 1)Output:returns the loss of the model, which is a scalar"""return torch.mean((Yhat-Y)**2) # mean((error)^2)3.3 预览最佳拟合线
创建函数后,可以使用绘图预览最佳拟合线,并且可以创建标准函数以供将来使用。它将以红色显示最佳拟合线,以橙色显示每个输入的预测,以蓝色显示预期输出。
def plot_lbf():"""Output:plots the line of best fit in comparison to the training data"""# plot the pointsplt.scatter(X,Y)# predictions for the line of best fitYhat = model(w, X)plt.scatter(X, Yhat, zorder=3) # plot the predictions# plot the line of best fitX_plot = torch.arange(-1,11+0.1,.1) # generate values with a step of .1plt.plot(X_plot, model(w, X_plot), color="red", zorder=0)plt.xlim(-1, 11)plt.xlabel("$X$")plt.ylabel("$Y$")plt.title(f"MSE: {MSE(Yhat, Y):.2f}")plt.show()plot_lbf()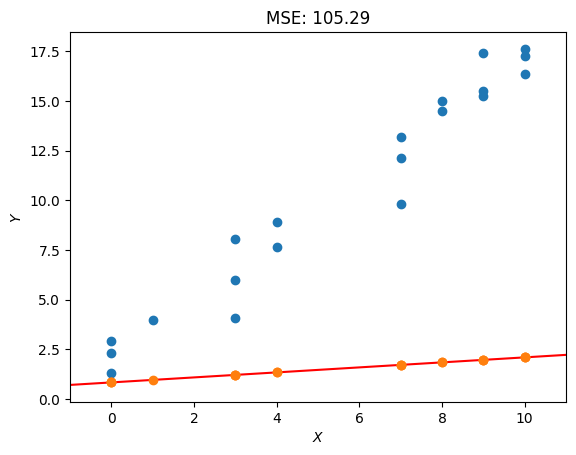
具有当前权重的输出并不理想,因为MSE为105.29。为了获得更好的MSE,需要选择不同的权重。它们可以再次随机化,但获得完美线的机会很小。这是梯度下降算法可用于以定义的方式更改权重值的地方。
3.4 梯度下降
梯度下降算法的解释可以在这里找到:梯度下降的简单介绍。在继续之前应阅读本文以避免混淆。
![]()
总结一下这篇文章,梯度下降使用成本函数的梯度来揭示每个权重对其的方向和影响。通过使用学习率缩放梯度并从每个权重的当前值中减去梯度,成本函数最小化,迫使模型的预测尽可能接近预期输出。
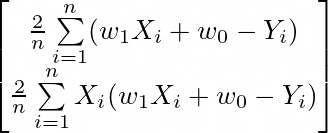
对于简单的线性回归,f 将是 MSE。Python 实现可以在下面看到。请记住,每个权重都有自己的偏导数用于公式,如上所示。
# optimizer
def gradient_descent(w):"""Inputs:w: array of weights | (num features + 1 bias, 1)Global Variables / Constants:X: array of inputs | (n samples, num features + 1 bias)Y: array of expected outputs | (n samples, 1)lr: learning rate to scale the gradientOutput:returns the updated weights""" n = len(X)# update the biasw[0] = w[0] - lr*2/n * torch.sum(model(w,X) - Y)# update the weightw[1] = w[1] - lr*2/n * torch.sum(X*(model(w,X) - Y))return w现在,该函数可用于更新权重。学习率是根据经验选择的,但它通常是一个较小的值。还可以绘制最佳拟合的新线。
lr = 0.01print("weights before:", w.flatten())
print("MSE before:", MSE(model(w,X), Y))# update the weights
w = gradient_descent(w)print("weights after:", w.flatten())
print("MSE after:", MSE(model(w,X), Y))plot_lbf()weights before: tensor([0.83, 0.13])
MSE before: tensor(105.29)
weights after: tensor([1.01, 1.46])
MSE after: tensor(2.99)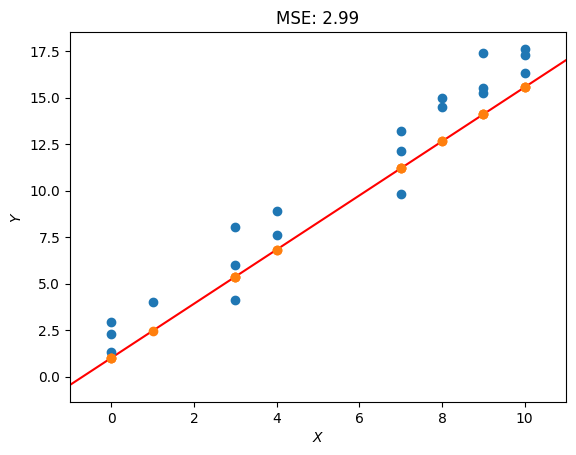
MSE 在第一次尝试时下降了 100 多分,但这条线仍然不能完全符合点数。请记住,目标是将 w₀ 设为 2,将 w₁ 设为 1.5。为了加快学习过程,可以再执行500次梯度下降,并且可以检查新结果。
# update the weights
for i in range(0, 500):# update the weightsw = gradient_descent(w)# print the new values every 10 iterationsif (i+1) % 100 == 0:print("epoch:", i+1)print("weights:", w.flatten())print("MSE:", MSE(model(w,X), Y))print("="*10)plot_lbf()epoch: 100
weights: tensor([1.44, 1.59])
MSE: tensor(1.31)
==========
epoch: 200
weights: tensor([1.67, 1.56])
MSE: tensor(1.25)
==========
epoch: 300
weights: tensor([1.80, 1.54])
MSE: tensor(1.24)
==========
epoch: 400
weights: tensor([1.87, 1.53])
MSE: tensor(1.23)
==========
epoch: 500
weights: tensor([1.91, 1.52])
MSE: tensor(1.23)
==========
500 个时期后,MSE 为 1.23。w₀ 为 1.91,w₁ 为 1.52。这意味着模型成功识别了最佳拟合线。可以执行其他更新,但添加到输出值的随机性可能会阻止模型实现完美的预测。
为了建立关于梯度下降如何工作的额外直觉,可以通过将它们与其输出 MSE 绘制来检查 w₀ 和 w₁ 的影响。绘制梯度下降的函数可以在附录中检查,输出可以在下面检查:
torch.manual_seed(5)
w = torch.rand(size=(2, 1))w0s, w1s, losses = list(),list(),list()# update the weights
for i in range(0, 500):if i == 0 or (i+1) % 10 == 0:w0s.append(float(w[0]))w1s.append(float(w[1]))losses.append(MSE(model(w,X), Y))# update the weightsw = gradient_descent(w)plot_GD([-2, 5.2], [-2, 5.2])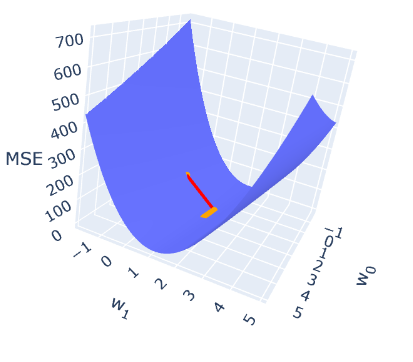
每个橙色点表示权重的更新,红线表示从一个迭代到下一个迭代的变化。最大的更新是从第一次迭代到第二次迭代,即红线。其他橙色点靠得很近,因为它们的衍生物很小,因此更新更小。该图显示了权重如何更新,直到获得最佳 MSE。
虽然这种方法很有用,但可以通过几种方式简化。首先,它没有利用矩阵乘法,这将简化模型的方程。其次,梯度下降不是回归的闭式解,因为每个问题的 epoch 数和学习率都不同,并且解是近似的。本文的最后一部分将解决第一个问题,下一篇文章将解决第二个问题。
四、另一种方法
虽然这种方法很有用,但它并不像它可能的那么简单。它不利用矩阵。截至目前,整个方程 Ŷ = Xw₁+ w₀ 用于模型的函数,并且必须单独计算每个权重的偏导数以进行梯度下降。通过使用矩阵运算和微积分,这两个函数都简化了。
首先,X 的形状为 (n 个样本,num 特征),w 的形状为 (num 特征 + 1 个偏差,1)。通过在 X 中添加额外的列,可以使用矩阵乘法,因为它将具有 (n 个样本、num 特征 + 1 个偏差)的新形状。这可以是一列将乘以偏差的列,这将缩放向量。这相当于广播偏差,这是先前计算预测的方式。
X = torch.hstack((torch.ones(X.shape),X))
Xtensor([[ 1., 9.],[ 1., 10.],[ 1., 0.],[ 1., 3.],[ 1., 8.],[ 1., 8.],[ 1., 0.],[ 1., 4.],[ 1., 1.],[ 1., 0.],[ 1., 7.],[ 1., 9.],[ 1., 3.],[ 1., 7.],[ 1., 9.],[ 1., 7.],[ 1., 3.],[ 1., 10.],[ 1., 10.],[ 1., 4.]]) 这会将等式更改为 Ŷ = X₁w₁+ X₀w₀。展望未来,偏差可以被视为一个特征,因此 num 特征可以表示自变量和偏差,并且可以省略 + 1 偏差。因此,X 的大小为 (n 个样本,num 特征),w 的大小为 (num features,1)。当它们相互相乘时,输出是预测向量,其大小为 (n 个样本,1)。矩阵乘法的输出与 相同。w[1]*X + w[0]
torch.manual_seed(5)
w = torch.rand(size=(2, 1))torch.matmul(X, w)tensor([[1.97],[2.09],[0.83],[1.21],[1.84],[1.84],[0.83],[1.33],[0.96],[0.83],[1.71],[1.97],[1.21],[1.71],[1.97],[1.71],[1.21],[2.09],[2.09],[1.33]])考虑到这一点,可以更新模型的功能:
# line of best fit
def model(w, X):"""Inputs:w: array of weights | (num features, 1)X: array of inputs | (n samples, num features)Output:returns the output of X@w | (n samples, 1)"""return torch.matmul(X, w)由于不再将每个权重视为单个分量,因此梯度下降算法也可以更新。基于梯度下降的简单介绍,矩阵的梯度下降算法如下:
![]()
这可以通过 PyTorch 轻松实现。由于 w 在文章开头被重塑,因此导数的输出需要重新整形以进行减法。
# optimizer
def gradient_descent(w):"""Inputs:w: array of weights | (num features, 1)Global Variables / Constants:X: array of inputs | (n samples, num features)Y: array of expected outputs | (n samples, 1)lr: learning rate to scale the gradientOutput:returns the updated weights | (num features, 1)""" n = X.shape[0]return w - (lr * 2/n) * (torch.matmul(-Y.T, X) + torch.matmul(torch.matmul(w.T, X.T), X)).reshape(w.shape)使用 500 个 epoch,可以生成与以前相同的输出:
lr = 0.01# update the weights
for i in range(0, 501):# update the weightsw = gradient_descent(w)# print the new values every 10 iterationsif (i+1) % 100 == 0:print("epoch:", i+1)print("weights:", w.flatten())print("MSE:", MSE(model(w,X), Y))print("="*10)epoch: 100
weights: tensor([1.43, 1.59])
MSE: tensor(1.31)
==========
epoch: 200
weights: tensor([1.66, 1.56])
MSE: tensor(1.25)
==========
epoch: 300
weights: tensor([1.79, 1.54])
MSE: tensor(1.24)
==========
epoch: 400
weights: tensor([1.87, 1.53])
MSE: tensor(1.23)
==========
epoch: 500
weights: tensor([1.91, 1.53])
MSE: tensor(1.23)
==========由于这些函数不需要为每个要素手动添加其他变量,因此可用于多元线性回归和多项式回归。
五、结论
下一篇文章将讨论不近似权重的回归闭式解决方案。相反,最小化的值将使用 Python 中的机器学习简介:Python 中回归的正态方程直接计算。
请不要忘记点赞和关注!:)
七、引用
- plot 3D 绘图
六、附录
绘制梯度下降
此函数利用 Plotly 在三维空间中显示梯度下降。
import plotly.graph_objects as go
import plotly
import plotly.express as pxdef plot_GD(w0_range, w1_range):"""Inputs:w0_range: weight range [w0_low, w0_high]w1_range: weight range [w1_low, w1_high]Global Variables:X: array of inputs | (n samples, num features + 1 bias)Y: array of expected outputs | (n samples, 1)lr: learning rate to scale the gradientOutput:prints gradient descent""" # generate all the possible weight combinations (w0, w1)w0_plot, w1_plot = torch.meshgrid(torch.arange(w0_range[0],w0_range[1],0.1),torch.arange(w1_range[0],w1_range[1],0.1))# rearrange into coordinate pairsw_plot = torch.hstack((w0_plot.reshape(-1,1), w1_plot.reshape(-1,1)))# calculate the MSE for each pairmse_plot = [MSE(model(w, X), Y) for w in w_plot]# plot the datafig = go.Figure(data=[go.Mesh3d(x=w_plot[:,0], y=w_plot[:,1],z=mse_plot,)])# plot gradient descent on loss functionfig.add_scatter3d(x=w0s, y=w1s, z=losses, marker=dict(size=3,color="orange"),line=dict(color="red",width=5))# prepare ranges for plottingxaxis_range = [w0 + 0.01 if w0 < 0 else w0 - 0.01 for w0 in w0_range] yaxis_range = [w1 + 0.01 if w1 < 0 else w1 - 0.01 for w1 in w1_range] fig.update_layout(scene = dict(xaxis_title='w<sub>0</sub>', yaxis_title='w<sub>1</sub>', zaxis_title='MSE',xaxis_range=xaxis_range,yaxis_range=yaxis_range))fig.show()七、参考和引用
- plot 3D 绘图
- 亨特·菲利普斯
相关文章:
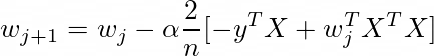
机器学习简介[01/2]:简单线性回归
Python 中的机器学习简介:简单线性回归 一、说明 简单线性回归为机器学习提供了优雅的介绍。它可用于标识自变量和因变量之间的关系。使用梯度下降,可以训练基本模型以拟合一组点以供未来预测。 二、技术背景 这是涵盖回归、梯度下降、分类和机器学习的其…...

Kubernetes技术--k8s核心技术yaml资源编排
(1).引入 我们可以使用kubectl实现单行指令的操作,但是这样做的坏处是不复用,所以为了更好的实现对一系列资源的编排工作。kuberntes中使用一种叫做资源清单文件(yaml)来实现对资源管理和资源对象编排部署。 (2).概述 yaml是一种标记语言。为了强调这种语言以数据做为中心,而…...

clickhouse-配置解释
详细内容看官网文档 一、全局服务配置 1.配置详解 名称含义默认值allow_use_jemalloc_memory允许使用 jemalloc 内存1(布尔)asynchronous_heavy_metrics_update_period_s更新异步指标的时间段(以秒为单位)120asynchronous_metr…...

基于亚马逊云科技无服务器服务快速搭建电商平台——性能篇
使用 Serverless 构建独立站的优势 在传统架构模式下,如果需要进行电商大促需要提前预置计算资源以支撑高并发访问,会造成计算资源浪费并且增加运维工作量。本文介绍一种新的部署方式,将 WordPress 和 WooCommerce 部署在 Amazon Lambda 中。…...

LINQ详解(查询表达式)
什么是LINQ? LINQ(语言集成查询)是将查询功能直接集成到C#中。数据查询表示简单的字符串,在编译时不会进行类型检查和IntelliSense(代码补全辅助工具)支持。 在开发中,通常需要对不同类型的数据源了解不同的查询语句,如SQL数据库…...

【DEVOPS】现状篇
0. 目录 1. 前言2. 现状2.1 需求管理2.2 开发流程2.3 测试流程2.4 部署流程2.5 维护阶段 3. 后记4. 相关 1. 前言 一直以来,深感内部工程化能力欠缺,急于将事情向前推进,总是希望能够向前走几步,再走几步。 可惜的是,…...

Linux文件管理知识:查找文件(第二篇)
Linux文件管理知识:查找文件(第二篇) 上篇文章详细介绍了linux系统中查找文件的工具或者命令程序locate和find命令的基本操作。那么,今天这篇文章紧接着查找文件相关操作内容介绍。 Find命令所属操作列表中的条目,有助于我们想要…...
医疗小程序:让服务更高效,用户体验更优化
随着移动互联网的快速发展,小程序已经成为了一个热门的开发方向。医疗健康类小程序也不例外,拥有广泛的市场需求和前景。本文将为你提供一份完整的医疗健康类小程序开发攻略,帮助你快速开发上线一个专业成熟的小程序商城。 一、选择合适的小程…...

C++11 std::transform函数使用说明
std::transform是C标准库中的一个算法,它用于对输入范围内的元素进行操作,并将结果存储在输出范围内。这个算法特别适合于将一种数据类型转换为另一种数据类型。 函数定义在头文件algorithm中 std::transform的基本语法如下: std::transfor…...

JavaScript-DOM查询
获取元素节点 获取元素节点的子节点 元素节点的属性 节点的修改 JavaScript中的DOM(文档对象模型)是一种编程接口,它允许JavaScript与HTML文档交互。创建DOM查询,可以使用多种方法. 获取元素节点 1. getElementById() – 通…...

大数据-玩转数据-Flink 水印
一、Flink 中的水印 在Flink的流式操作中, 会涉及不同的时间概念: 1.1 处理时间 是指的执行操作的各个设备的时间,对于运行在处理时间上的流程序, 所有的基于时间的操作(比如时间窗口)都是使用的设备时钟。比如, 一个长度为1个小时的窗口将会包含设备…...

【Apollo】阿波罗自动驾驶系统:驶向未来的智能出行(含源码安装)
前言 Apollo (阿波罗)是一个开放的、完整的、安全的平台,将帮助汽车行业及自动驾驶领域的合作伙伴结合车辆和硬件系统,快速搭建一套属于自己的自动驾驶系统。 开放能力、共享资源、加速创新、持续共赢是 Apollo 开放平台的口号。百度把自己所拥有的强大、…...

网络-Netty
how pipeline.addLast(ChannelHandler)...

如何使用vue-smooth-dnd
Vue Smooth DnD是一个基于Vue的平滑易用的拖放库。它提供了简单易用的API和可自定义的样式。 要使用Vue Smooth DnD,可以按照以下步骤进行操作: 安装Vue Smooth DnD npm install vue-smooth-dnd --save 在组件中引入Vue Smooth DnD import VueSmoot…...

为AWS认证做好准备:一份全面的备考指南
随着云计算的快速发展,越来越多的专业人士选择获取AWS(亚马逊网络服务)认证。这个认证不仅可以证明你对AWS的理解和专业技能,还有助于你在云计算领域获得更好的工作机会。 以下是一份全面的备考指南,帮助你为AWS认证做…...

尚硅谷SpringMVC
九、HttpMessageConverter...

django的简易的图书管理系统jsp书店进销存源代码MySQL
本项目为前几天收费帮学妹做的一个项目,Java EE JSP项目,在工作环境中基本使用不到,但是很多学校把这个当作编程入门的项目来做,故分享出本项目供初学者参考。 一、项目描述 django的简易的图书管理系统 系统有1权限:…...

力扣125. 验证回文串
125. 验证回文串 如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。 字母和数字都属于字母数字字符。 给你一个字符串 s,如果它是 回文串 ,返回 true &…...

用WebStorm创建Mock数据
WebStorm是一款强大的集成式开发环境,它集成了许多实用的功能,包括Mock数据的创建。 下面是用WebStorm创建Mock数据的步骤: 打开WebStorm,选择一个项目或新建一个项目;在项目中创建一个名为“mock”的文件夹…...

Python钢筋混凝土结构计算.pdf-已知弯矩确定混凝土梁截面尺寸
计算原理 确定混凝土梁截面的合理尺寸通常需要考虑弯矩、受力要求和约束条件等多个因素。以下是一种常见的计算公式,用于基于已知弯矩确定混凝土梁截面的合理尺寸: 请注意,以上公式仅提供了一种常见的计算方法,并且具体的规范和设…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
