精读《算法题 - 地下城游戏》
今天我们看一道 leetcode hard 难度题目:地下城游戏。
恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
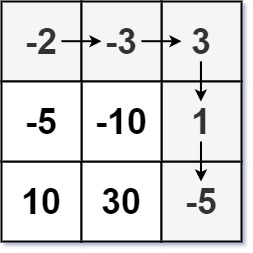
输入:
dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]输出:
7解释:如果骑士遵循最佳路径:右 -> 右 -> 下 -> 下 ,则骑士的初始健康点数至少为 7 。
思考
挺像游戏的一道题,首先只能向下或向右移动,所以每个格子可以由上面或左边的格子移动而来,很自然想到可以用动态规划解决。
再想一想,该题必须遍历整个地下城而无法取巧,因为最低健康点数无法由局部数据算出,这是因为如果不把整个地下城走完,肯定不知道是否有更优路线。
动态规划
二维迷宫用两个变量 i j 定位,其中 dp[i][j] 描述第 i 行 j 列所需的最低 HP。
但最低所需 HP 无法推断出是否能继续前进,我们还得知道当前 HP 才行,比如:
// 从左到右走
3 -> -5 -> 6 -> -9在数字 6 的位置所需最低 HP 是 3,但我们必须知道在 6 时勇者剩余 HP 才能判断 -9 会不会直接导致勇者挂了,因此我们将 dp[i][j] 结果定义为一个数组,第一项表示当前 HP,第二项表示初始所需最低 HP。
代码实现如下:
function calculateMinimumHP(dungeon: number[][]): number {// dp[i][j] 表示 i,j 位置 [当前HP, 所需最低HP]const dp = Array.from(dungeon.map(item => () => [0, 0]))// dp[i][j] = 所需最低HP最低(dp[i-1][j], dp[i][j-1])dp[0][0] = [dungeon[0][0] > 0 ? 1 + dungeon[0][0] : 1,dungeon[0][0] > 0 ? 1 : 1 - dungeon[0][0]]for (let i = 0; i < dungeon.length; i++) {for (let j = 0; j < dungeon[0].length; j++) {if (i === 0 && j === 0) {continue}const paths = []if (i > 0) {paths.push([i - 1, j])}if (j > 0) {paths.push([i, j - 1])}const pathResults = paths.map(path => {let leftMaxHealth = dp[path[0]][path[1]][0] + dungeon[i][j]// 剩余HP大于 0 则无需刷新最低HP,否则尝试刷新取最大值let lowestNeedHealth = dp[path[0]][path[1]][1]if (leftMaxHealth <= 0) {// 最低要求HP补上差价lowestNeedHealth += 1 - leftMaxHealth// 最低需要HP已补上,所以剩余HP也变成了 1leftMaxHealth = 1}return [leftMaxHealth, lowestNeedHealth]})// 找到 pathResults 中 lowestNeedHealth 最小项let minLowestNeedHealth = Infinitylet minIndex = 0pathResults.forEach((pathResult, index) => {if (pathResult[1] < minLowestNeedHealth) {minLowestNeedHealth = pathResult[1]minIndex = index}})dp[i][j] = [pathResults[minIndex][0], pathResults[minIndex][1]]}}return dp[dungeon.length - 1][dungeon[0].length - 1][1]
};首先计算初始位置 dp[0][0],因为只看这一个点,因此如果有恶魔,最少初始 HP 为能击败恶魔后自己剩 1 HP 就行了,如果房间是空的,至少自己 HP 得是 1(否则勇者进迷宫之前就挂了),如果有魔法球,那么初始 HP 为 1(一样防止进迷宫前挂了)。
初始 HP 稍有不同,如果房间是空的或者有恶魔,那打完恶魔之后最多剩 1 HP 最经济,所以此时 HP 初始值就是 1,如果有魔法球,那么一方面为了防止进入迷宫前自己就挂了,得有个初始 1 的 HP,魔法球又必须得吃,所以 HP 是 1 + 魔法球。
接着就是状态转移方程了,由于 dp[i][j] 可以由 dp[i-1][j] 或 dp[i][j-1] 移动得到(注意 i 或 j 为 0 时的场景),因此我们判断一下从哪条路过来的最低初始 HP 最低就行了。
如果进入当前房间后,房间是空的,有魔法球,或者当前 HP 可以打败恶魔,则不影响最低初始 HP,如果当前 HP 不足以击败恶魔,则我们把缺的 HP 给勇者在初始时补上,此时极限一些还剩 1 HP,得到一个最经济的结果。
然后我们提交代码发现,无法 AC!下面是一个典型挂掉的例子:
1 -3 3
0 -2 0
-3 -3 -3我们把 DP 中间过程输出,发现右下角的 5 大于最优答案 3.
[[ 2, 1 ], [ 1, 3 ], [ 4, 3 ][ 2, 1 ], [ 1, 2 ], [ 1, 2 ][ 1, 3 ], [ 1, 5 ], [ 1, 5 ]
]观察发现,勇者先往右走到头,再往下走到头答案就是 3,问题出在 i=1,j=2 处,也就是中间行最右列的 [1, 2]。但从这一点来看,勇者从左边过来比从上面过来需要的初始 HP 少,因为左边是 [1, 2] 上面是 [4, 3],但这导致了答案不是最优解,因为此时剩余 HP 不够,右下角是一个攻击为 3 的恶魔,而如果此时我们选择了初始 HP 高一些的 [4, 3],换来了更高的当前 HP,在不用补初始 HP 的情况就能把右下角恶魔干掉,整体是更划算的。
如果此时我们在玩游戏,读读档也就能找到最优解了,但悲剧的是我们在写一套算法,我们发现当前 DP 项居然还可能由后面的值(攻击力为 3 的恶魔)决定! 用专业的话来说就是有后效性导致无法使用 DP。
我们在判断每一步最优解时,其实有两个同等重要的因素影响判断,一个是初始最少所需 HP,它的重要度不言而喻,我们最终就希望这个答案尽可能小;但还有当前 HP 呢,当前 HP 高意味着后面的路会更好走,但我们如果不往后看,就不知道后面是否有恶魔,自然也不知道要不要留着高当前 HP 的路线,所以根本就无法根据前一项下结论。
因为考虑的因素太多了,我们得换成游戏制作者的视角,假设作为游戏设计者,而不是玩家,你会真的从头玩一遍吗?如果真的要设计这种条件很极限的地下城,设计者肯定从结果倒推啊,结果我们勇者就只剩 1 HP 了,至于路上会遇到什么恶魔或者魔法球,反过来倒推就一切尽在掌握了。所以我们得采用从右下角开始走的逆向思维。
逆向思维
为什么从结果倒推,DP 判断条件就没有后效性了呢?
先回忆一下从左上角出发的情况,为什么除了最低初始 HP 外还要记录当前 HP?原因是当前 HP 决定了当前房间的怪物勇者能否打得过,如果打不过,我们得扩大最低初始 HP 让勇者能在仅剩 1 HP 的情况险胜当前房间的恶魔。但这个当前 HP 值不仅要用来辅助计算最低初始 HP,它还有一个越大越好的性质,因为后面房间可能还有恶魔,得留一些 HP 预防风险,而 "最低初始 HP" 尽可能低与 "当前 HP" 尽可能高,这两个因素无法同时考虑。
那为什么从右下角,以终为始的考虑就可以少判断一个条件了呢?首先最低初始 HP 我们肯定要判断的,因为答案要的就是这个,那当前 HP 呢?当前 HP 重要吗?不重要,因为你已经拯救到公主了,而且是以最低 HP 1 点的状态救到了公主,按故事路线逆着走,遇到恶魔房间,恶魔攻击是多少我就给你加多少初始 HP,遇到魔法球恢复了我就给你扣对应初始 HP,总之能让你正好战胜恶魔,魔法球补给你的 HP 我也扣掉,就可以了。核心区别是,此时当前 HP 已经不会影响最低初始 HP 了,因为初始 HP 就是从头推的,我们反着走地下城,每次实际上都是在判断这个点作为起点时的状态,所以与之前的路径无关。
代码很简单,如下:
function calculateMinimumHP(dungeon: number[][]): number {// dp[i][j] 表示 i,j 位置最少HPconst dp = Array.from(dungeon.map(item => () => [0, 0]))// 右下角起始 HP 1,遇到怪物加血,遇到魔法球扣血,实际上就是 -dungeon 计算const si = dungeon.length - 1const sj = dungeon[0].length - 1dp[si][sj] = dungeon[si][sj] > 0 ? 1 : 1 - dungeon[si][sj]for (let i = si; i >= 0; i--) {for (let j = sj; j >= 0; j--) {if (i === si && j === sj) {continue}const paths = []if (i < si) {paths.push([i + 1, j])}if (j < sj) {paths.push([i, j + 1])}const pathResults = paths.map(path => dp[path[0]][path[1]] - dungeon[i][j])// 选出最小 HP 作为 dp[i][j],但不能小于 1dp[i][j] = Math.max(Math.min(...pathResults), 1)}}return dp[0][0]
};逆向思维为什么就能减少当前 HP(或者说路径和,或者说所有之前节点的影响)判断呢?我猜你大概率还是没彻底明白。因为这个思考非常关键,可以说是这道题 99% 的困难所在,还是画个图解释一下:
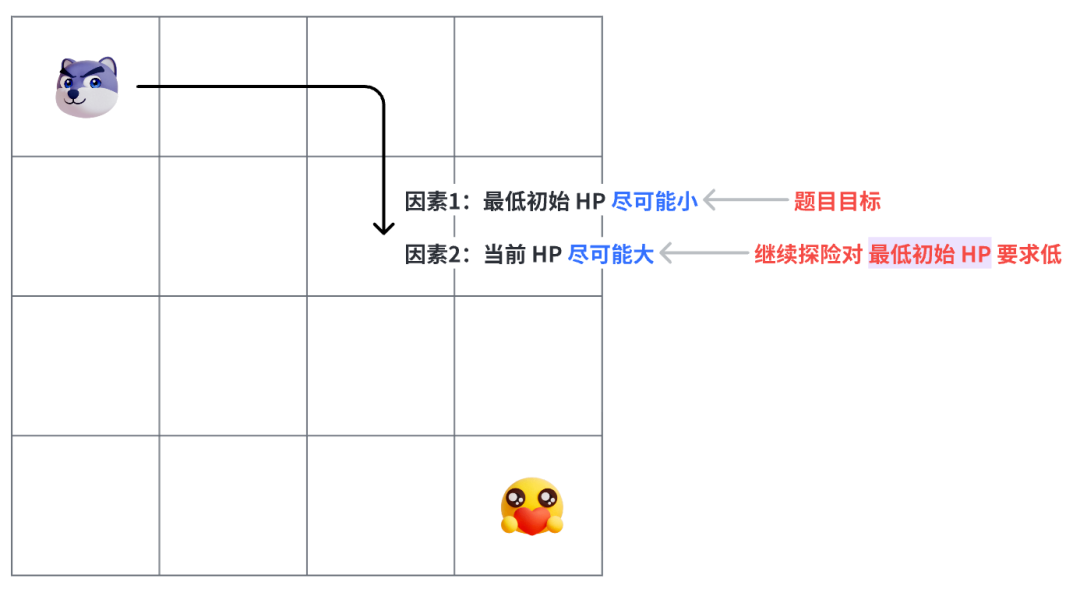
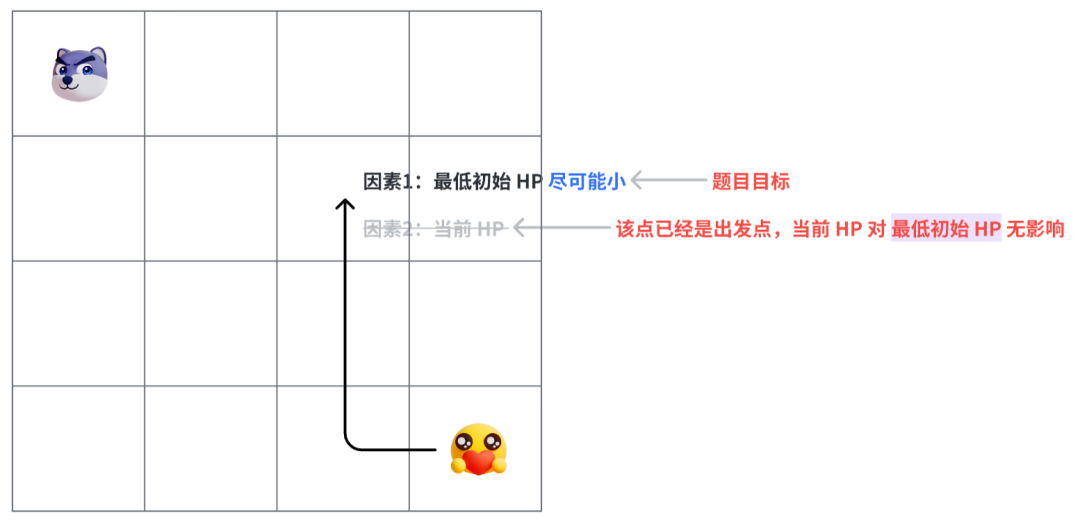
上图是勇者正常探险的思路,下面是逆向(或公主救勇者)的思路。
总结
该题很容易想到使用动态规划解决,但因为目标是求最低的初始健康点需求,所以按照勇者路径走的话,后续未探索的路径会影响到目标,所以我们需要从公主角度反向寻找勇者,才可以保证动态规划的每个判断点都只考虑一个影响因素。
讨论地址是:精读《算法 - 地下城游戏》· Issue #498 · dt-fe/weekly
如果你想参与讨论,请 点击这里,每周都有新的主题,周末或周一发布。前端精读 - 帮你筛选靠谱的内容。
版权声明:自由转载-非商用-非衍生-保持署名(创意共享 3.0 许可证)
相关文章:

精读《算法题 - 地下城游戏》
今天我们看一道 leetcode hard 难度题目:地下城游戏。 恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。 骑士…...

随记-Kibana Dev Tools,ES 增删改查 索引,Document
索引 创建索引 创建索引 PUT index_test创建索引 并 修改分片信息 # 创建索引 并 修改分片信息 PUT index_test2 { # 必须换行, PUT XXX 必须独占一行,类似的 其他请求也需要独占一行 "settings": {"number_of_shards": 1, # 主分片"…...

什么是架构,架构的本质是什么
不论是开发人员还是架构师,我们都一直在跟软件系统打交道,架构是在工作中出现最频繁的术语之一。那么,到底什么是架构?你可能有自己的答案,也有可能没有答案。对“架构”的理解需要我们不断在实践中思考、归纳、演绎&a…...
Python爬虫(十七)_糗事百科案例
糗事百科实例 爬取糗事百科段子,假设页面的URL是: http://www.qiushibaike.com/8hr/page/1 要求: 使用requests获取页面信息,用XPath/re做数据提取获取每个帖子里的用户头像连接、用户姓名、段子内容、点赞次数和评论次数保存到json文件内…...

Ae 效果:CC Threads
生成/CC Threads Generate/CC Threads CC Threads(CC 编织条)效果基于当前图层像素生成编织条图案和纹理。可以用在各种设计中,如背景设计、图形设计、文字设计等。 ◆ ◆ ◆ 效果属性说明 Width 宽度 设置编织的宽度。 默认值为 50。值越大…...
)
Kotlin 协程 - 多路复用 select()
一、概念 又叫选择表达式,是一个挂起函数,可以同时等待多个挂起结果,只取用最快恢复的那个值(即多种方式获取数据,哪个更快返回结果就用哪个)。 同时到达 select() 会优先选择先写子表达式,想随…...
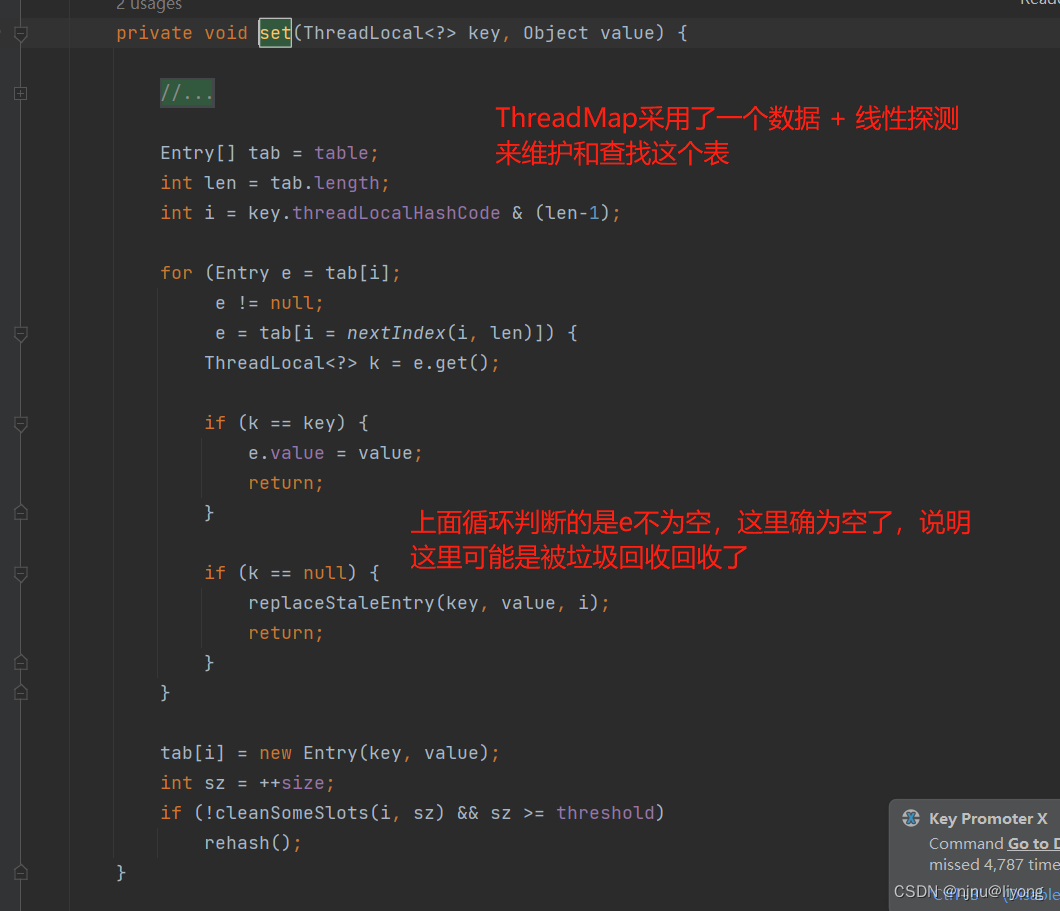
学习笔记-ThreadLocal
ThreadLocal 什么是ThreadLocal? ThreadLocal 是线程本地变量类,在多线程并行执行过程中,将变量存储在ThreadLocal中,每个线程中都有独立的变量,因此不会出现线程安全问题。 应用举例 解决线程安全问题:例…...

python利用pandas统计分析—groupby()函数的使用
文章目录 一、groupby使用场景二、groupby基本原理三、groupby分组运算基础聚合操作:只能选择一种聚合操作agg 聚合操作:可以针对同列选择不同聚合方法transformapply 四、groupby分组后去重统计nunique()五、groupby分组后重命名列名rename()直接重新命…...

OPENCV实现ORB特征检测
# -*- coding:utf-8 -*- """ 作者:794919561 日期:2023/8/31 """ import cv2 import numpy as np# 读图像 img = cv2.imread(F:\\learnOpenCV\\openCVLearning\\pictures\\chess.jpg)...
W5100S-EVB-PICO主动PING主机IP检测连通性(十)
前言 上一章节我们用我们开发板在UDP组播模式下进行数据回环测试,本章我们用开发板去主动ping主机IP地址来检测与该主机之间网络的连通性。 什么是PING? PING是一种命令, 是用来探测主机到主机之间是否可通信,如果不能ping到某台…...

使用 Nginx 搭建文件下载服务器
文章目录 一、基础环境二、适用场景三、方法和步骤四、其他说明 版权声明:本文为CSDN博主「杨群」的原创文章,遵循 CC 4.0 BY-SA版权协议,于2023年8月27日首发于CSDN,转载请附上原文出处链接及本声明。 原文链接:http…...

链式栈StackT
C关键词:内部类/模板类/头插 C自学精简教程 目录(必读) C数据结构与算法实现(目录) 栈的内存结构 空栈: 有一个元素的栈: 多个元素的栈: 成员函数说明 0 clear 清空栈 clear 函数负责将栈的对内存释放…...

Fiddler中 AutoResponder 使用
Fiddler的 AutoResponder ,即URL重定向功能非常强大。不管我们做URL重定向,还是做mock测试等,都可以通过该功能进行实践。 下面,小酋就来具体讲下该功能的用法。 Enable rules 启用规则Unmatched requests passthrough 没有匹配…...
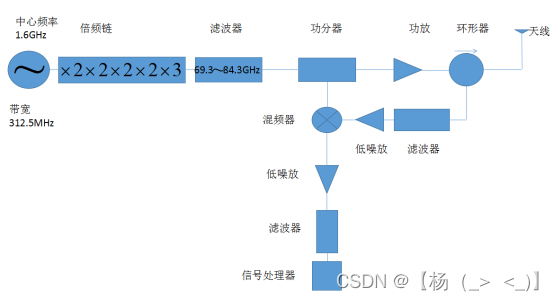
77GHz线性调频连续波雷达
文章目录 前言 一、背景 二、优缺点 三、工作原理 四、电路模块设计 4.1.LFMCW信号源 4.2.发射电路 4.3.接收电路 4.4.信号处理器 五、应用 5.1.汽车测距 5.2.军事方面 5.3.气象方面 总结 前言 这篇文章是博主本科期间整理的关于77GHz线性调频连续波雷达的相关资料,…...

YOLOV8改进:更换为MPDIOU,实现有效涨点
1.该文章属于YOLOV5/YOLOV7/YOLOV8改进专栏,包含大量的改进方式,主要以2023年的最新文章和2022年的文章提出改进方式。 2.提供更加详细的改进方法,如将注意力机制添加到网络的不同位置,便于做实验,也可以当做论文的创新点。 2.涨点效果:更换为MPDIOU,实现有效涨点! 目录…...
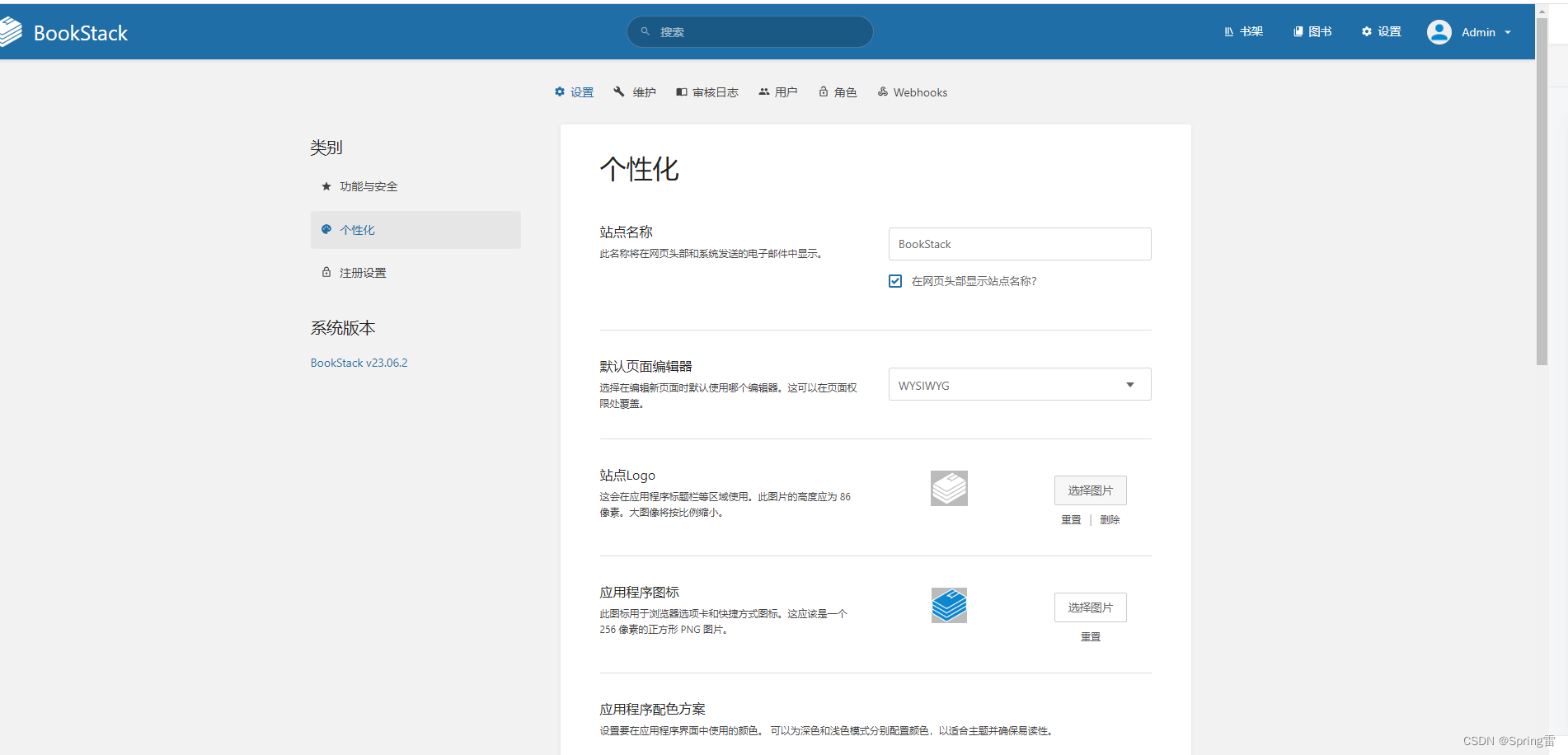
BookStack开源免费知识库docker-compose部署
BookStack(书栈)是一个功能强大且易于使用的开源知识管理平台,适用于个人、团队或企业的文档协作和知识共享。 一、BookStack特点 简单易用:BookStack提供了一个直观的用户界面,使用户能够轻松创建、编辑和组织文档多…...
Linux:编译遇到 Please port gnulib freadahead.c to your platform ,怎么破
问题背景 编译m4时遇到以下错误,该怎么解决呢? 解决方法 进入m4的build目录:build/host-m4-1.4.17 输入命令: sed -i s/IO_ftrylockfile/IO_EOF_SEEN/ lib/*.c echo "#define _IO_IN_BACKUP 0x100" >> lib/std…...
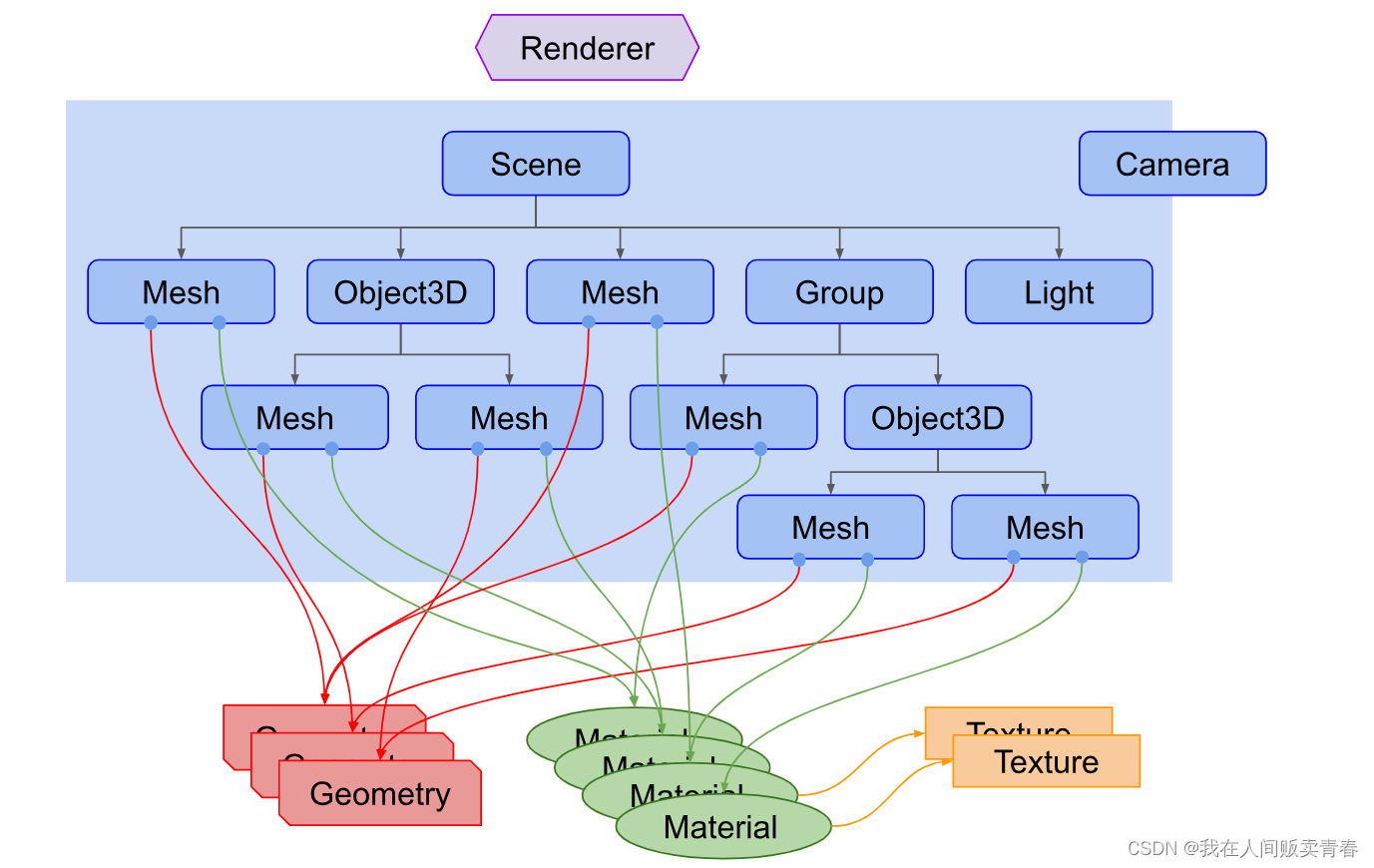
three.js(三):three.js的渲染结构
three.js 的渲染结构 概述 three.js 封装了场景、灯光、阴影、材质、纹理和三维算法,不必在直接用WebGL 开发项目,但有的时候会间接用到WebGL,比如自定义着色器。three.js 在渲染三维场景时,需要创建很多对象,并将它…...
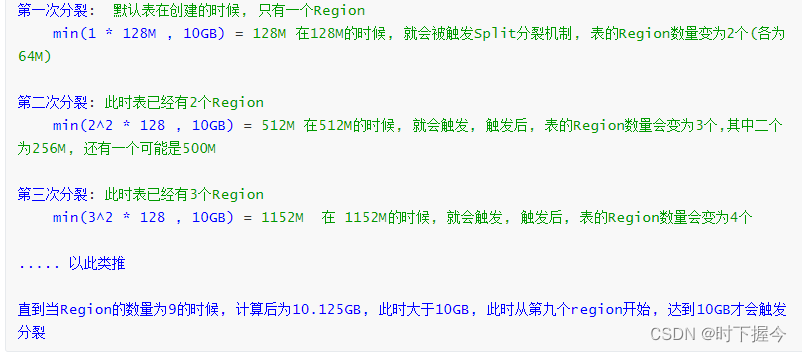
客户端读写HBase数据库的运行原理
1.HBase的特点 HBase是一个数据库,与RDMS相比,有以下特点: ① 它不支持SQL ② 不支持事务 ③ 没有表关系,不支持JOIN ④ 有列族,列族下可以有上百个列 ⑤ 单元格,即列值,可以存储多个版本的值&…...
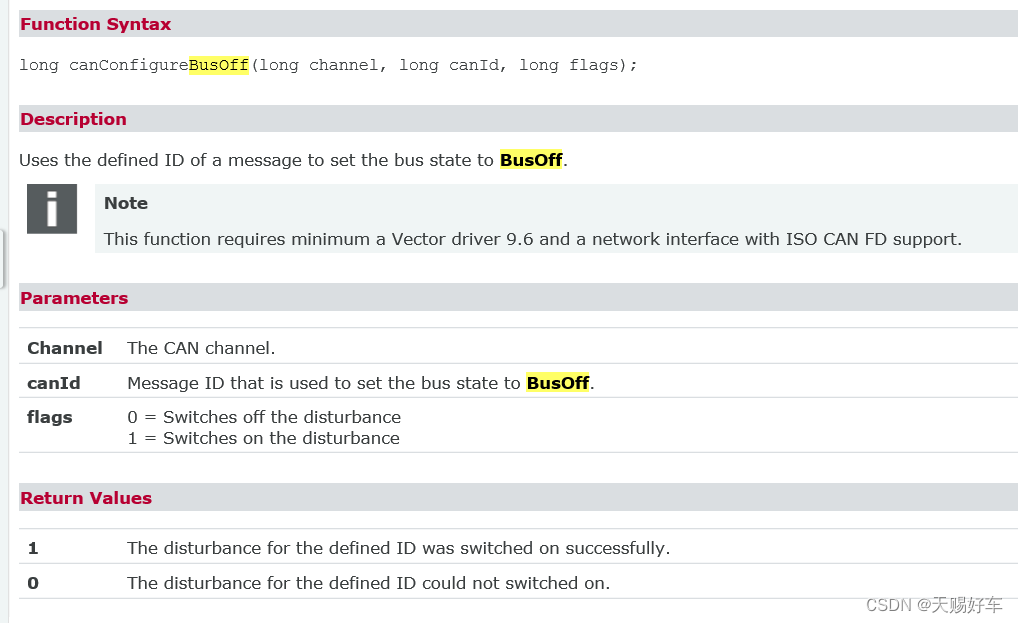
不使用VH6501设备,通过VN1630等普通设备使用canConfigureBusOff函数进行busoff干扰测试
** 特别注意一下,使用这个函数需要你的vector驱动在9.6以上以及支持 ISO CAN FD. ** 函数canConfigureBusOff 可以通过脚本的形式产生bus off,而VH6501可以通过干扰bit位来产生bus off(使用CANoe Demo - CANDisturbanceMain进行Bus Off测试)。 对于函数canConfigureBusOf…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
