AcWing1018.最低通行费
1018.最低通行费
一个商人穿过一个 N×N 的正方形的网格,去参加一个非常重要的商务活动。
他要从网格的左上角进,右下角出。
每穿越中间 1 个小方格,都要花费 1 个单位时间。
商人必须在 (2N−1)(2−1) 个单位时间穿越出去。
而在经过中间的每个小方格时,都需要缴纳一定的费用。
这个商人期望在规定时间内用最少费用穿越出去。
请问至少需要多少费用?
注意:不能对角穿越各个小方格(即,只能向上下左右四个方向移动且不能离开网格)。
输入格式
第一行是一个整数,表示正方形的宽度 N。
后面 N 行,每行 N个不大于 100 的正整数,为网格上每个小方格的费用。
输出格式
输出一个整数,表示至少需要的费用。
数据范围
1≤N≤100
输入样例:
5
1 4 6 8 10
2 5 7 15 17
6 8 9 18 20
10 11 12 19 21
20 23 25 29 33输出样例:
109样例解释
样例中,最小值为 109=1+2+5+7+9+12+19+21+33
看完这道题就知道是道dp的题。
直接写dp方程:
状态表示
f[i][j]表示从左下角到位置 [i,j]的最小值
也就是,f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w;
而第 i 层的答案只依赖于第 i 层和第 i - 1 层,容易想到滚动数组优化
在看到方程,发现不用滚动数组,直接用一维存即可(具体解释见代码)
一维转移:f[j] = max(f[j], f[j - 1]) + w;
答案表示
用二维存就是 f[n][m]
用一维存就是 f[m]
注意这道题是求最小值,所以要注意边界条件
AC代码:
#include <stdio.h>
int f[110][110], a[110][110];
int min(int a, int b)
{return a > b ? b : a;
}
int main()
{int n, i, j;scanf("%d", &n);for(i = 1; i <= n; i++)for(j = 1; j <= n; j++)scanf("%d", &a[i][j]);f[1][1] = a[1][1];for(i = 2; i <= n; i++) f[i][1] = f[i - 1][1] + a[i][1];for(j = 2; j <= n; j++) f[1][j] = f[1][j - 1] + a[1][j];for(i = 2; i <= n; i++)for(j = 2; j <= n; j++)f[i][j] = min(f[i - 1][j], f[i][j - 1]) + a[i][j];printf("%d", f[n][n]);return 0;
}相关文章:

AcWing1018.最低通行费
1018.最低通行费一个商人穿过一个 NN 的正方形的网格,去参加一个非常重要的商务活动。他要从网格的左上角进,右下角出。每穿越中间 1 个小方格,都要花费 1 个单位时间。商人必须在 (2N−1)(2−1) 个单位时间穿越出去。而在经过中间的每个小方…...

【面试题】vue中的插槽是什么?
大厂面试题分享 面试题库后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库一、slot是什么在HTML中 slot 元素 ,作为 Web Components 技术套件的一部分,是Web组件内的一个占位符该占位符可以在后期…...

Go语言结构体struct详解,Go空结构体的这些妙用你知道吗?
本文详解了Go语言结构体的各个知识点,最后介绍了空结构体的3种妙用。希望对你有帮助。 定义 结构体,是一种自定义的数据类型,由多个数据类型组合而成。用于描述一类事物相关属性。 定义方式: type 类型名 struct {字段名 字段类…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 航天器(Python) | 机试题+算法思路+考点+代码解析 【2023】
航天器 题目 给航天器一侧加装长方形和正方形的太阳能板(图中的斜线区域); 需要先安装两个支柱(图中的黑色竖条); 再在支柱的中间部分固定太阳能板; 但航天器不同位置的支柱长度不同; 太阳能板的安装面积受限于最短一侧的那支支柱的长度; 现提供一组整型数组的支柱高度数据;…...

【Optional】告别丑陋判空,使用Optional类
一、概述 当项目中充斥着大量的、丑陋的判空语句,如下: if (user ! null) {Address address user.getAddress();if (address ! null) {Country country address.getCountry();if (country ! null) {String isocode country.getIsocode();if (isocod…...
魔兽世界服务端端新手搭建教程
明杰也是很久以前开始研究魔兽服务器架设,主要原因是亚服经常要排队6-7个小时,去不排除的服和单机没啥区别,以怀旧服玩到10级以后就开始玩335端,一开始也和新入手的人一样云里雾里的,经过长时间的学习总算有点成就,向新…...
宝塔搭建实战人才求职管理系统mobile手机端vue源码(五)
大家好啊,我是测评君,欢迎来到web测评。 上一期给大家分享骑士cms会员管理member前端vue在本地运行打包、宝塔发布部署的方式,本期给大家分享,mobile移动端vue怎么在本地运行,打包,实现线上功能更新替换的方…...

生态应用:探讨 NGINX 与上下游系统集成时的开发经验
NGINX 作为一款高性能的 Web 服务器和反向代理服务器,在各种应用场景中广泛应用。随着业务的发展,我们在使用 NGINX 时,可能需要将其与其他系统进行集成,以实现更加复杂的业务需求。 本文将结合实际应用场景,探讨 NGI…...
ArcGIS批量拼接大量栅格遥感影像:Mosaic工具
本文介绍在ArcGIS下属的ArcMap软件中,基于Mosaic工具,批量对大量栅格遥感影像文件加以拼接、镶嵌的方法。 在GIS应用中,我们时常需要对大量栅格遥感影像数据加以批量拼接的工作。这一步骤可以基于Python语言实现,具体可以参考文章…...

Flink UI部署jar包报错
错误描述: 通过Flink的UI中的Submit New Job菜单添加jar包的时候提示报错。报错信息的关键字是“The LocalStreamEnvironment cannot be used when submitting a program through a client, or running in a TestEnvironment context”,最关键的是“Loc…...

Linux就该这么学:RAID与LVM磁盘阵列技术
这里写目录标题 7.1.1 部署磁盘阵列7.1.2 损坏磁盘阵列及修复7.1.3 磁盘阵列+备份盘7.1.4 删除磁盘阵列1. 需要将所有的磁盘都设置成停用状态:2. 逐一移除出去3. 续停用整个RAID磁盘阵列7.2 LVM逻辑卷管理器7.2.1 部署逻辑卷7.2.2 扩容逻辑卷7.2.3 缩小逻辑卷7.2.4 逻辑卷快照…...
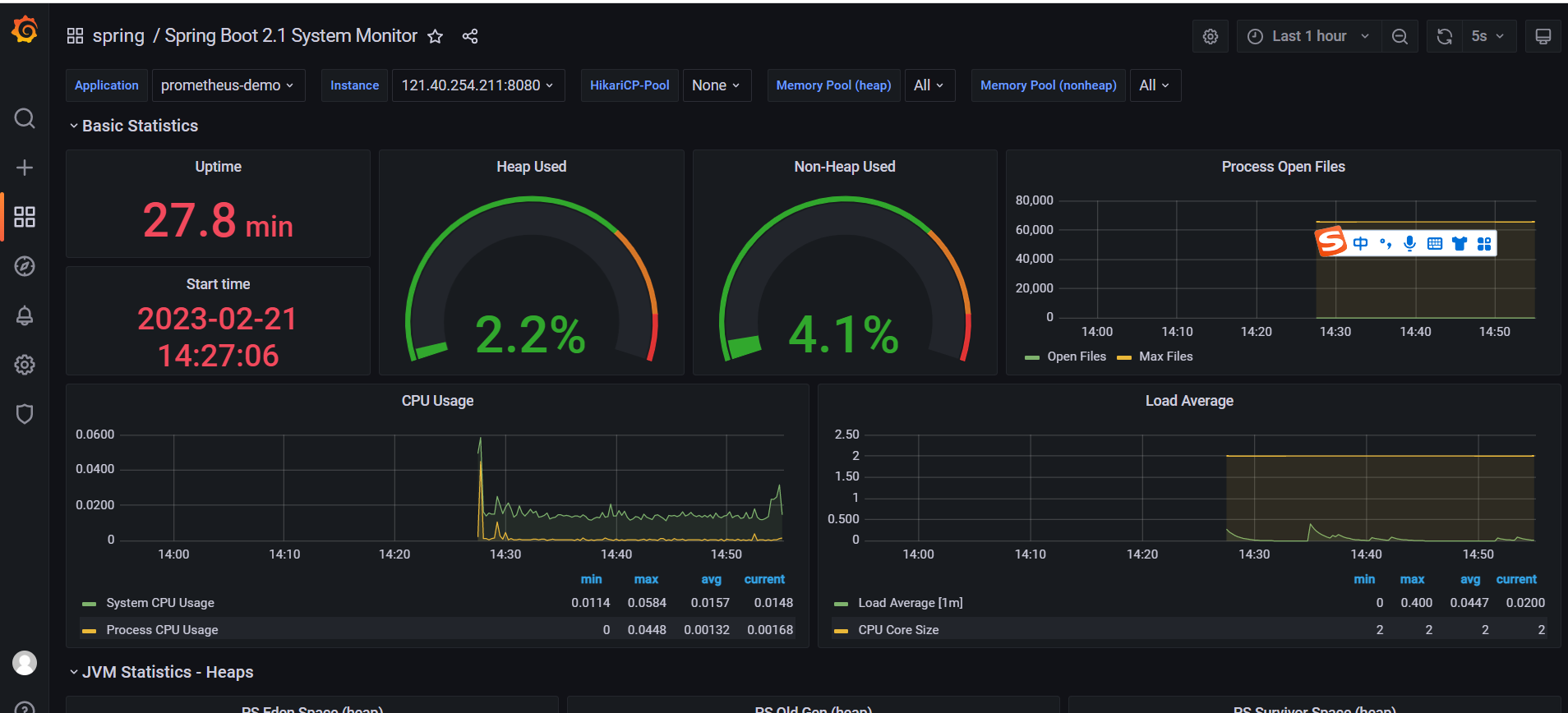
Prometheus+Grafana监控
1、简介1.1 Prometheus官网地址:https://prometheus.io/Prometheus是一个开源的监控系统,起源于SoundCloud。它由以下几个核心组件构成:数据爬虫: 根据配置的时间定期的通过HTTP抓去metrics数据。time-series 数据库: …...

【JUC2022】第三章 线程中断与 LockSupport
【JUC2022】第三章 线程中断与 LockSupport 文章目录【JUC2022】第三章 线程中断与 LockSupport一、线程中断1.什么是中断机制2.中断 API3.代码实现4.Thread.sleep()二、LockSupport1.什么是 LockSupport2.代码实现3.总结一、线程中断 1.什么是中断机制 首先,一个…...
:202快乐数、1两数之和、454四数相加II、15三数之和、18四树之和)
数据结构刷题(七):202快乐数、1两数之和、454四数相加II、15三数之和、18四树之和
1.快乐数题目链接思路:使用set,当set中出现相同元素时,返回false注意:while循环中语句顺序; 除数取余。解法:public boolean isHappy(int n){Set<Integer> res new HashSet<>();int[] arr ne…...
)
华为机试题:HJ80 整型数组合并(python)
文章目录知识点详解1、input():获取控制台(任意形式)的输入。输出均为字符串类型。 1.1、int(input()) 与 map(int, input().spilt()) 的区别 1.2、input() 与 list(input()) 的区别、及其相互转换方法2、print() :打印输出…...
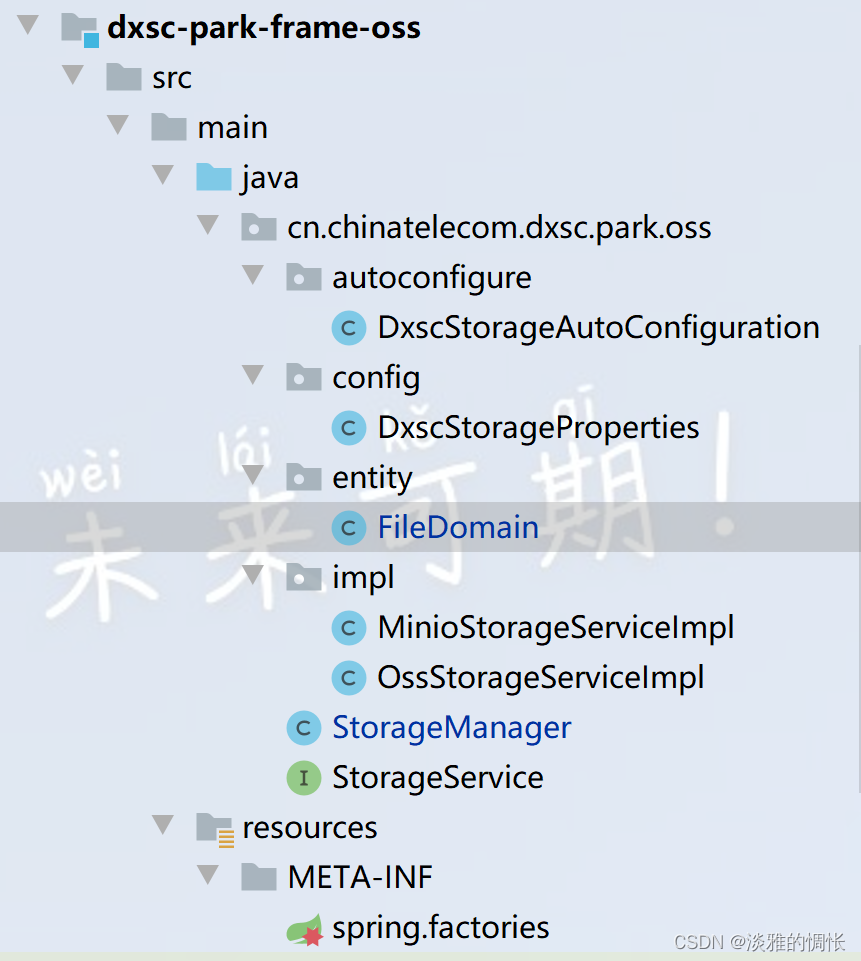
spring boot——自定义依赖实现自动配置
需求 要实现的功能是:实现一个可以支持miniooss两种方式,上传下载文件的自定义依赖。其中还包括一些创建桶、删除桶、删除文件等功能,但是最主要的是实现自动配置。 如果对spring理解很深的话,自动配置这些东西很容易理解&#…...

QMap 判断是否value是否已经存在,结合Sleep函数测试
网上查了资料,基本说的都是通过.value判断是否已经之前的key值,但是尝试.了一下发现有.key的函数,对比着来就感觉这个函数是用来判断是否已经存在value值,于是开始百度也几乎没有找到相关资料,只好自己看官方文档&…...
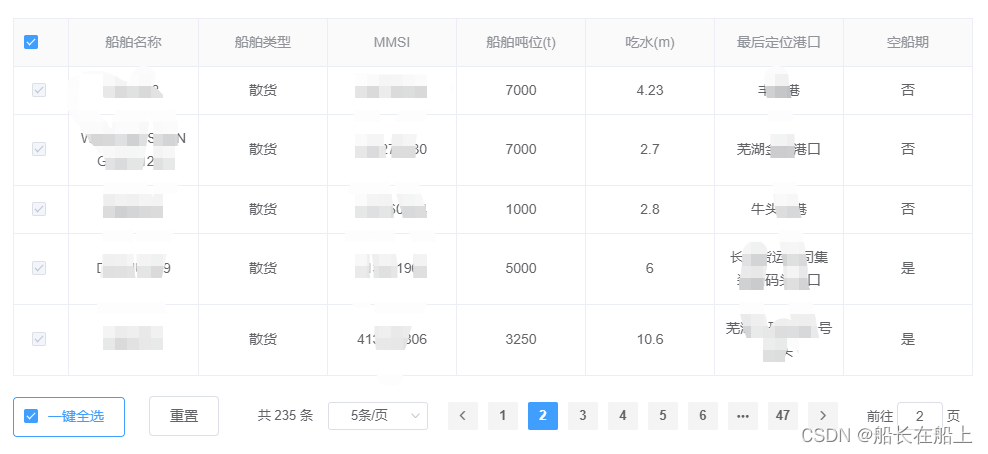
vue后台管理系统项目-table选择多行数据分页列表、一键全选重置功能
table选择多行数据 功能介绍: 1.列表分页功能; 2.一键全选,选中列表所有数据; 3.全选,选中当前页数据; 4.重置,清除选中状态; 5.列表搜索查询; 效果: 1.列表分…...
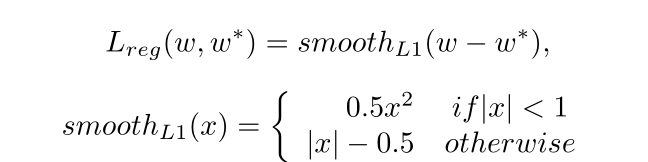
论文解读 | [CVPR2019] 基于自适应文本区域表示的任意形状场景文本检测
目录 1 研究背景及意义 2 总体设计 3 方法论 3.1 自适应文本区域表示 3.2 文本建议 3.3 建议改进 4 损失函数 5 实验及结果 1 研究背景及意义 现有的场景文本检测方法使用固定点数的多边形来 表示文本区域。例如,水平文本使用2个点(左上/右下)表示文本区域&…...

2月编程语言排行榜谁还没有看?
近日,TIOBE公布了2023年2月编程语言排行榜,本月各个语言表现如何?谁又摘得桂冠?一起来看看吧! TIOBE 2月Top15编程语言: 详细榜单查看TIOBE官网 https://www.tiobe.com/tiobe-index/ 关注IT行业的小伙伴们…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
