剑指 Offer 28. 对称的二叉树
剑指 Offer 28. 对称的二叉树
难度:easy\color{Green}{easy}easy
题目描述
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
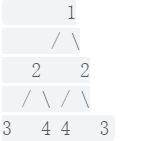
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
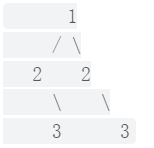
示例 1:
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
输入:root = [1,2,2,null,3,null,3]
输出:false
限制:
0<=节点个数<=10000 <= 节点个数 <= 10000<=节点个数<=1000
注意:本题与主站 101 题相同:https://leetcode-cn.com/problems/symmetric-tree/
算法
(递归)
对称二叉树定义:
-
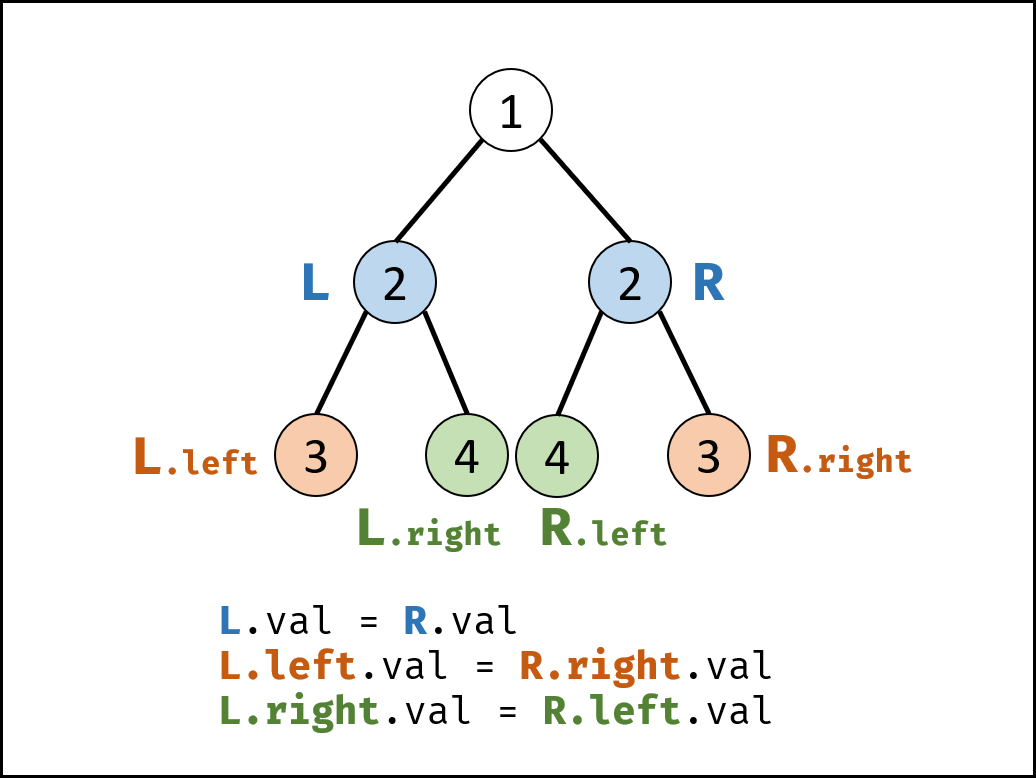
对于树中 任意两个对称节点 L 和 R ,一定有:
- L.val=R.val :即此两对称节点值相等。
- L.left.val=R.right.val :即 L 的 左子节点 和 R 的 右子节点 对称;
- L.right.val=R.left.val :即 L 的 右子节点 和 R 的 左子节点 对称。
-
根据以上规律,考虑从顶至底递归,判断每对节点是否对称,从而判断树是否为对称二叉树。
mirrTree(TreeNode* a, TreeNode* b)
终止条件:
- 当 L 和 R 有一个为空的时候: 判断如果此时都为空,返回 true,否则返回 false;
递推工作:
- 判断两节点 L.left 和 R.right 是否对称,即 mirrTree(L.left, R.right) ;
- 判断两节点 L.right 和 R.left 是否对称,即 mirrTree(L.right, R.left) ;
返回值: 两对节点都对称时,才是对称树,因此用与逻辑符 && 连接。
isSymmetric(root) :
- 特例处理: 若根节点 root 为空,则直接返回 true 。
- 返回值: 即 mirrTree(root.left, root.right) ;
复杂度分析
-
时间复杂度:O(n)O(n)O(n),其中 nnn 是二叉树的节点数量。
-
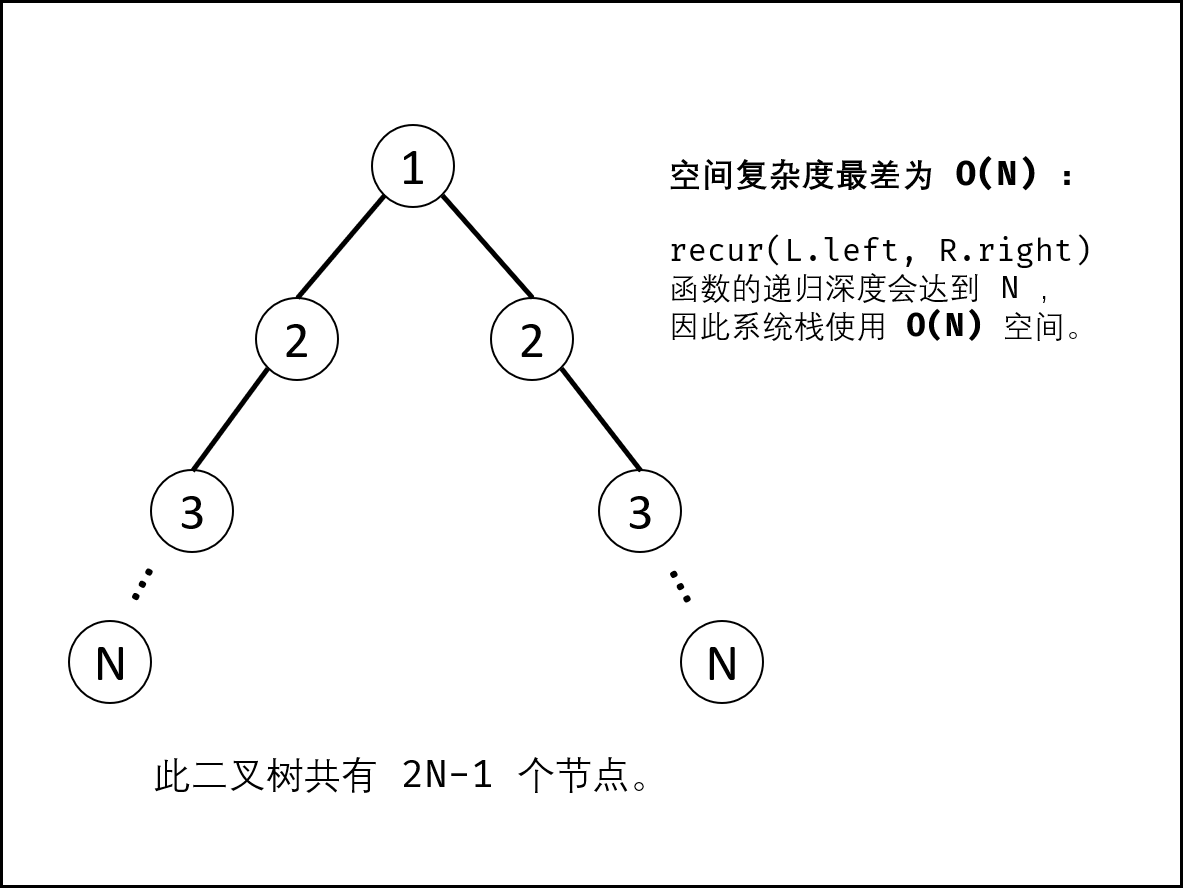
空间复杂度 : 最差情况下(见下图),二叉树退化为链表,系统使用 O(n)O(n)O(n) 大小的栈空间。
C++ 代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:bool isSymmetric(TreeNode* root) {if (!root) return true;return mirrTree(root->left, root->right);}bool mirrTree(TreeNode* a, TreeNode* b) {if (!a || !b) return !a && !b;if (a->val != b->val) return false;return mirrTree(a->left, b->right) && mirrTree(a->right, b->left);}
};
相关文章:

剑指 Offer 28. 对称的二叉树
剑指 Offer 28. 对称的二叉树 难度:easy\color{Green}{easy}easy 题目描述 请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。 例如,二叉树 [1,2,2,3,4,4,3] 是对称的。 但是下…...
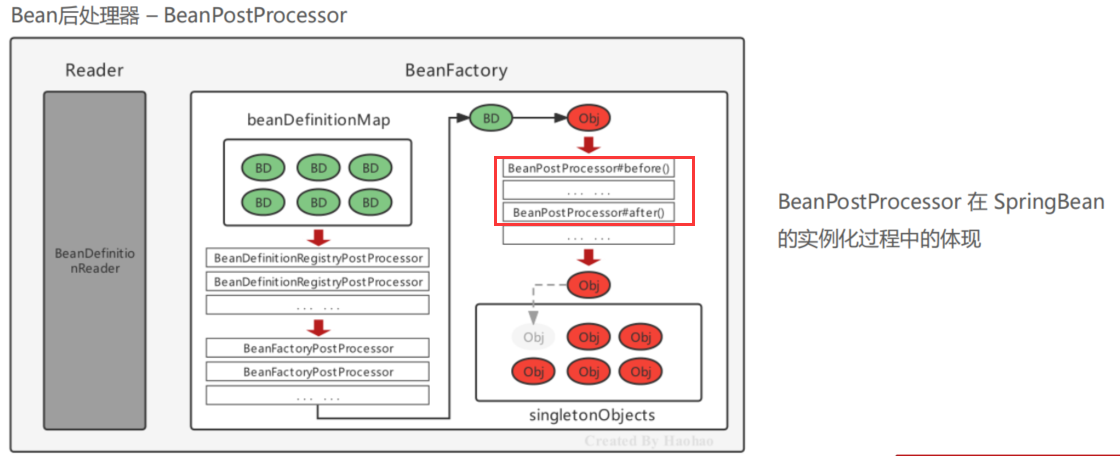
深入Spring底层透析后置处理器之豁然开朗篇
目录前言Spring的后置处理器Bean工厂后置处理器Bean后置处理器自定义Component实现注解开发前言 看这篇文章之前,需要了解Bean创建的过程,本篇文章是接着bean创建的基本流程的续写 Bean创建的基本过程:http://t.csdn.cn/1lK2d Spring的后置处…...
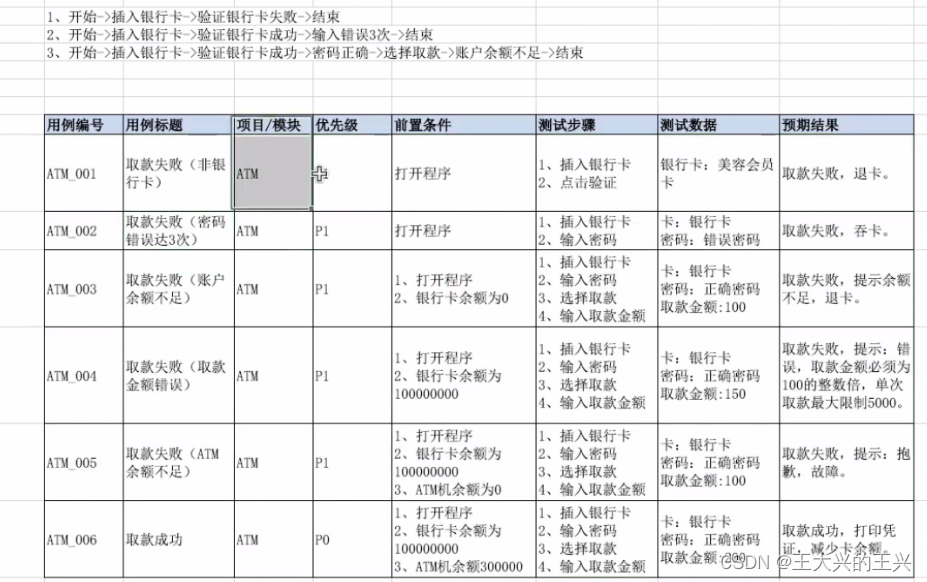
软件测试(基础定义篇)
测试基础 1、什么是软件测试?2、常见的测试分类3、质量模型 4、软件测试流程 5、测试用例 6、测试用例设计方法 )1、什么是软件测试? 1、什么是软件? 答:软件是控制计算机硬件工作的工具。 2、软件的组成? 3、什么是…...

华为OD机试 - 寻找目标字符串 | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 简易压缩算法(Python) | 机试题算法思路 【2023】 华为OD机试题 - 获取最大软件版本号(JavaScript) 华为OD机试 - 猜字谜(Python) | 机试题+算法思路 【2023】 华为OD机试 - 删除指定目录(Python) | 机试题算法思路 【2023】 华为OD机试 …...
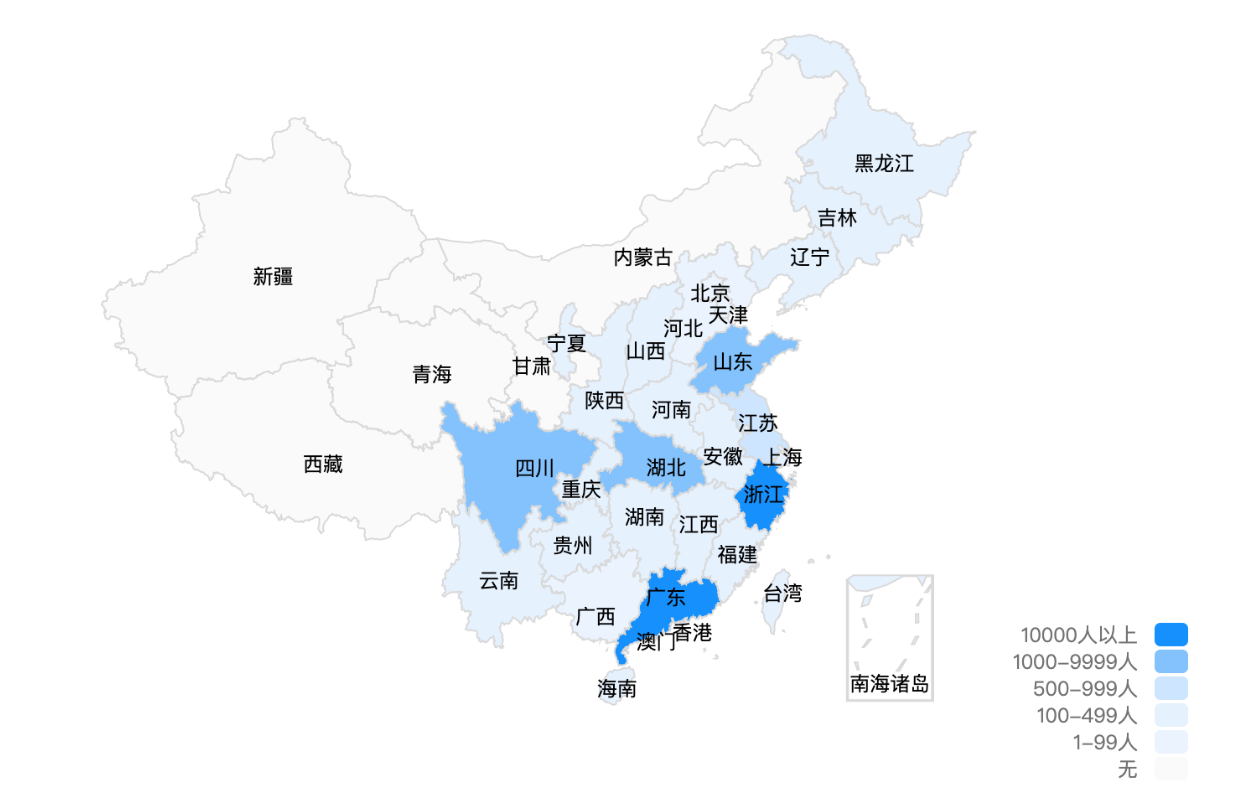
使用echart绘制中国地图并显示人数
文章目录引言效果如图所示vue中echarts4.9版本,地图的使用引言 在做毕设的过程中,有一个需求:根据用户的ip,在前端展示出中国地图,然后展现出每个省有多少人这样子 经过百度后,发现可以使用echart来完成该…...
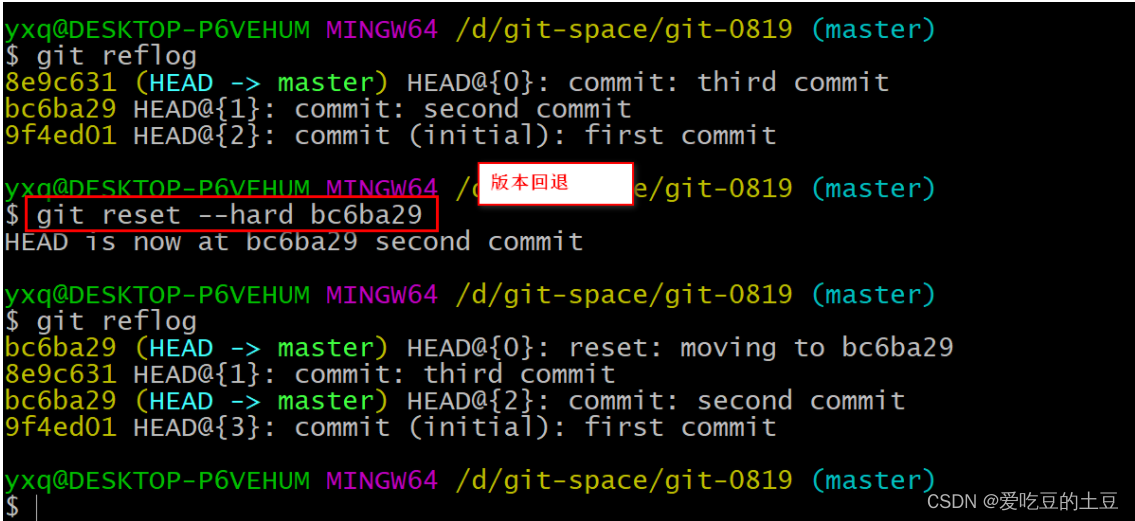
Git的常用命令
1:软件安装1.1:Git下载与安装百度上搜索Git官网:https://git-scm.com/下载:https://git-scm.com/download/win下载Git安装程序,双击安装 Git-2.9.3.2-64-bit.exe配置环境变量path 使用git --version查看 git 是否安装成…...

AcWing1018.最低通行费
1018.最低通行费一个商人穿过一个 NN 的正方形的网格,去参加一个非常重要的商务活动。他要从网格的左上角进,右下角出。每穿越中间 1 个小方格,都要花费 1 个单位时间。商人必须在 (2N−1)(2−1) 个单位时间穿越出去。而在经过中间的每个小方…...

【面试题】vue中的插槽是什么?
大厂面试题分享 面试题库后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库一、slot是什么在HTML中 slot 元素 ,作为 Web Components 技术套件的一部分,是Web组件内的一个占位符该占位符可以在后期…...

Go语言结构体struct详解,Go空结构体的这些妙用你知道吗?
本文详解了Go语言结构体的各个知识点,最后介绍了空结构体的3种妙用。希望对你有帮助。 定义 结构体,是一种自定义的数据类型,由多个数据类型组合而成。用于描述一类事物相关属性。 定义方式: type 类型名 struct {字段名 字段类…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 航天器(Python) | 机试题+算法思路+考点+代码解析 【2023】
航天器 题目 给航天器一侧加装长方形和正方形的太阳能板(图中的斜线区域); 需要先安装两个支柱(图中的黑色竖条); 再在支柱的中间部分固定太阳能板; 但航天器不同位置的支柱长度不同; 太阳能板的安装面积受限于最短一侧的那支支柱的长度; 现提供一组整型数组的支柱高度数据;…...

【Optional】告别丑陋判空,使用Optional类
一、概述 当项目中充斥着大量的、丑陋的判空语句,如下: if (user ! null) {Address address user.getAddress();if (address ! null) {Country country address.getCountry();if (country ! null) {String isocode country.getIsocode();if (isocod…...
魔兽世界服务端端新手搭建教程
明杰也是很久以前开始研究魔兽服务器架设,主要原因是亚服经常要排队6-7个小时,去不排除的服和单机没啥区别,以怀旧服玩到10级以后就开始玩335端,一开始也和新入手的人一样云里雾里的,经过长时间的学习总算有点成就,向新…...
宝塔搭建实战人才求职管理系统mobile手机端vue源码(五)
大家好啊,我是测评君,欢迎来到web测评。 上一期给大家分享骑士cms会员管理member前端vue在本地运行打包、宝塔发布部署的方式,本期给大家分享,mobile移动端vue怎么在本地运行,打包,实现线上功能更新替换的方…...

生态应用:探讨 NGINX 与上下游系统集成时的开发经验
NGINX 作为一款高性能的 Web 服务器和反向代理服务器,在各种应用场景中广泛应用。随着业务的发展,我们在使用 NGINX 时,可能需要将其与其他系统进行集成,以实现更加复杂的业务需求。 本文将结合实际应用场景,探讨 NGI…...
ArcGIS批量拼接大量栅格遥感影像:Mosaic工具
本文介绍在ArcGIS下属的ArcMap软件中,基于Mosaic工具,批量对大量栅格遥感影像文件加以拼接、镶嵌的方法。 在GIS应用中,我们时常需要对大量栅格遥感影像数据加以批量拼接的工作。这一步骤可以基于Python语言实现,具体可以参考文章…...

Flink UI部署jar包报错
错误描述: 通过Flink的UI中的Submit New Job菜单添加jar包的时候提示报错。报错信息的关键字是“The LocalStreamEnvironment cannot be used when submitting a program through a client, or running in a TestEnvironment context”,最关键的是“Loc…...

Linux就该这么学:RAID与LVM磁盘阵列技术
这里写目录标题 7.1.1 部署磁盘阵列7.1.2 损坏磁盘阵列及修复7.1.3 磁盘阵列+备份盘7.1.4 删除磁盘阵列1. 需要将所有的磁盘都设置成停用状态:2. 逐一移除出去3. 续停用整个RAID磁盘阵列7.2 LVM逻辑卷管理器7.2.1 部署逻辑卷7.2.2 扩容逻辑卷7.2.3 缩小逻辑卷7.2.4 逻辑卷快照…...
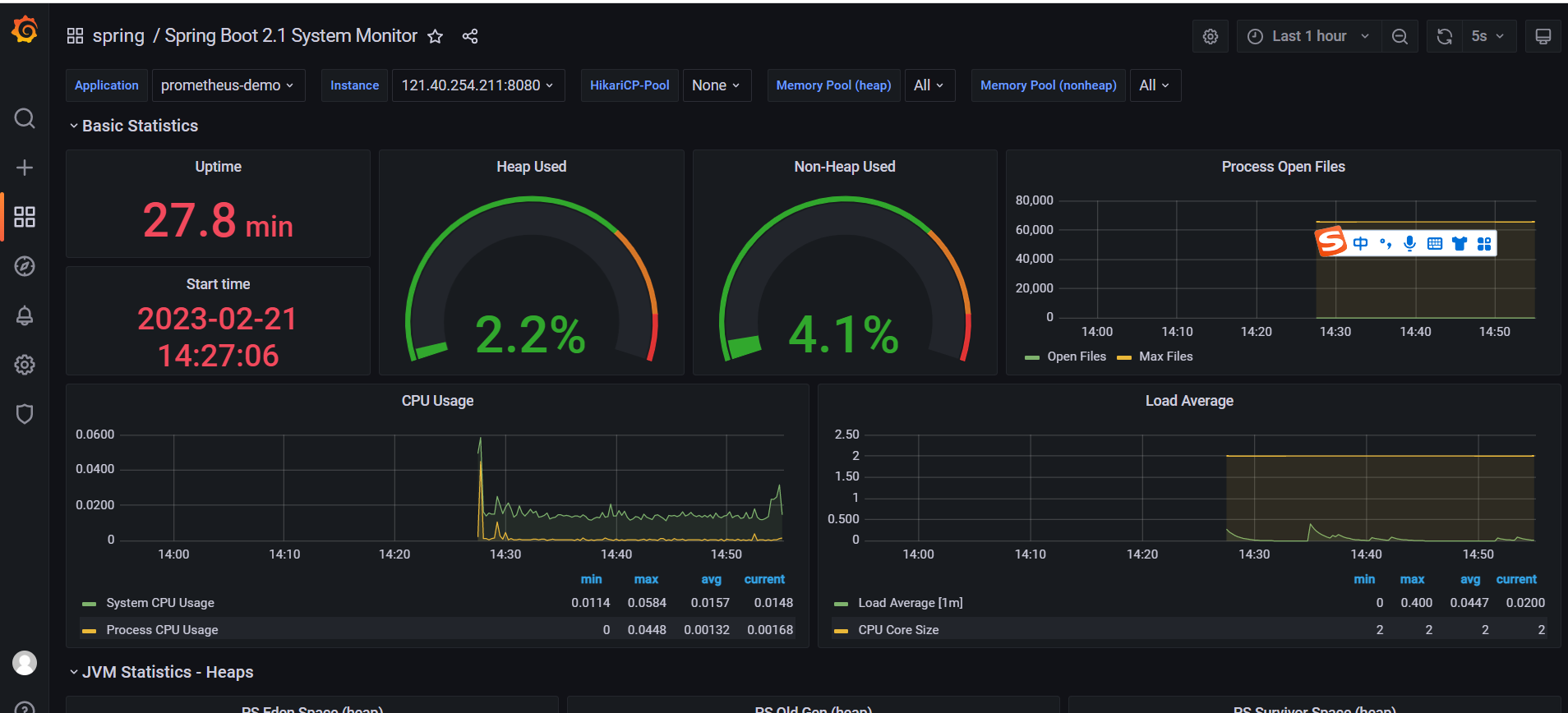
Prometheus+Grafana监控
1、简介1.1 Prometheus官网地址:https://prometheus.io/Prometheus是一个开源的监控系统,起源于SoundCloud。它由以下几个核心组件构成:数据爬虫: 根据配置的时间定期的通过HTTP抓去metrics数据。time-series 数据库: …...

【JUC2022】第三章 线程中断与 LockSupport
【JUC2022】第三章 线程中断与 LockSupport 文章目录【JUC2022】第三章 线程中断与 LockSupport一、线程中断1.什么是中断机制2.中断 API3.代码实现4.Thread.sleep()二、LockSupport1.什么是 LockSupport2.代码实现3.总结一、线程中断 1.什么是中断机制 首先,一个…...
:202快乐数、1两数之和、454四数相加II、15三数之和、18四树之和)
数据结构刷题(七):202快乐数、1两数之和、454四数相加II、15三数之和、18四树之和
1.快乐数题目链接思路:使用set,当set中出现相同元素时,返回false注意:while循环中语句顺序; 除数取余。解法:public boolean isHappy(int n){Set<Integer> res new HashSet<>();int[] arr ne…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

CppCon 2015 学习:Simple, Extensible Pattern Matching in C++14
什么是 Pattern Matching(模式匹配) ❝ 模式匹配就是一种“描述式”的写法,不需要你手动判断、提取数据,而是直接描述你希望的数据结构是什么样子,系统自动判断并提取。❞ 你给的定义拆解: ✴ Instead of …...
