用于设计和分析具有恒定近心点半径的低推力螺旋轨迹研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
本文可用于设计和分析具有恒定近心点半径的低推力螺旋轨迹。低推力轨迹设计是一种航天器轨道设计的方法,通过使用较小的推力在较长的时间内进行轨道转移,以实现目标轨道的变化。这种方法适用于需要节省燃料或对轨道精度要求较高的任务。
用户需要提供初始地球停泊轨道的经典轨道要素,这些要素包括轨道倾角、升交点赤经、近地点幅角、轨道倾角的变化率以及近地点幅角的变化率。此外,用户还需要提供最终或“目标”轨道的离心率,即目标轨道的形状。
航天器的轨道运动是使用修改的赤道坐标轨道要素进行建模。这些修改的赤道坐标轨道要素包括半长轴、离心率、倾角、升交点赤经和近地点幅角。通过使用这些轨道要素,可以准确地描述航天器在轨道上的位置和速度。
在进行轨道转移计算时,本脚本假设整个轨道转移过程中推力加速度是恒定的。这意味着航天器在整个轨道转移过程中以相同的推力加速度进行运动。这种简化假设可以简化计算过程,并得到近似的轨道解决方案。
此外,本脚本还假设轨道运动是开普勒运动或未受扰动的。这意味着在计算过程中不考虑其他天体或外力对航天器轨道的影响。这种假设适用于大多数低地球轨道任务,其中其他天体或外力的影响可以忽略不计。
可以设计和分析具有恒定近地点半径的低推力螺旋轨道,以满足特定任务的要求。这个代码提供了一个简单而有效的工具,可以帮助工程师和科学家在航天器轨道设计和分析方面取得更好的结果。
📚2 运行结果
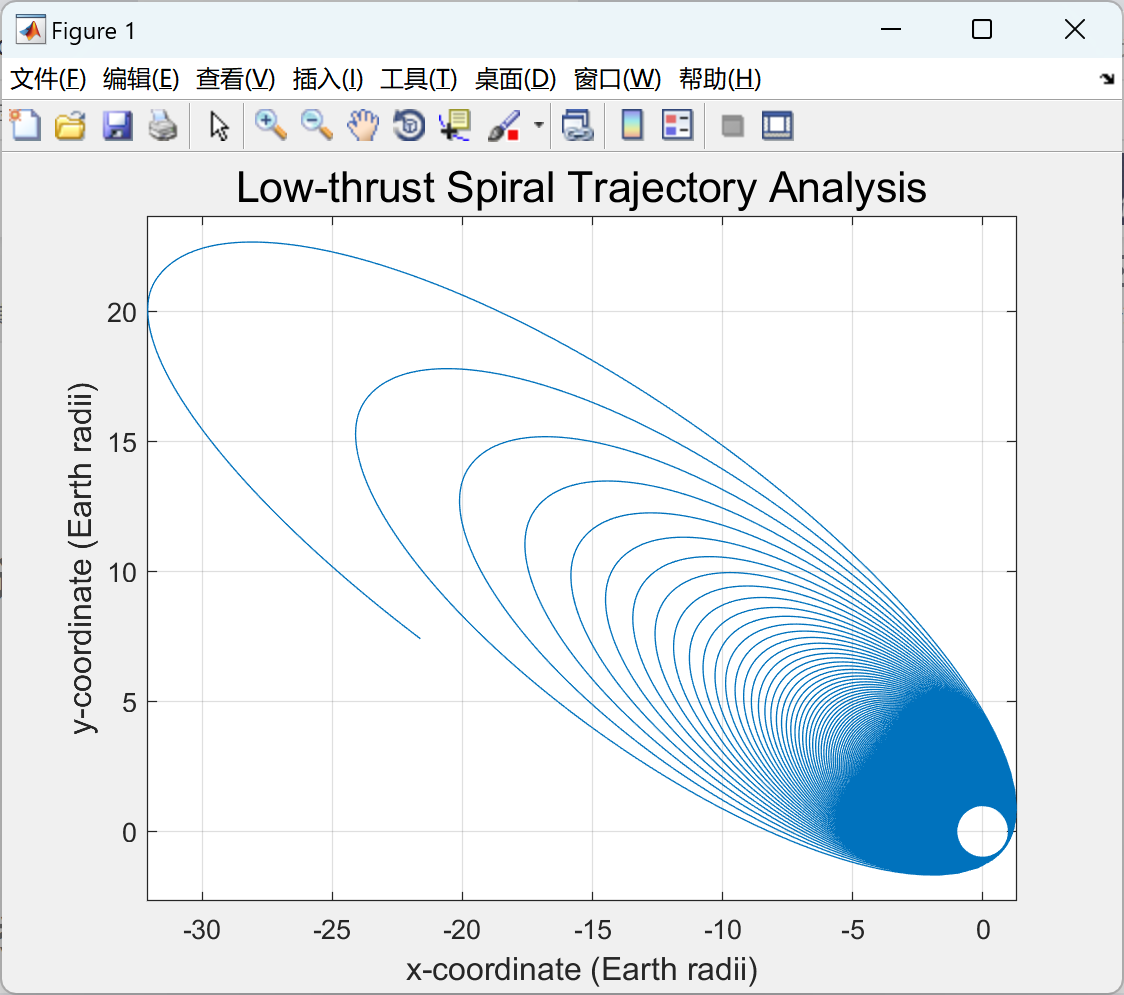



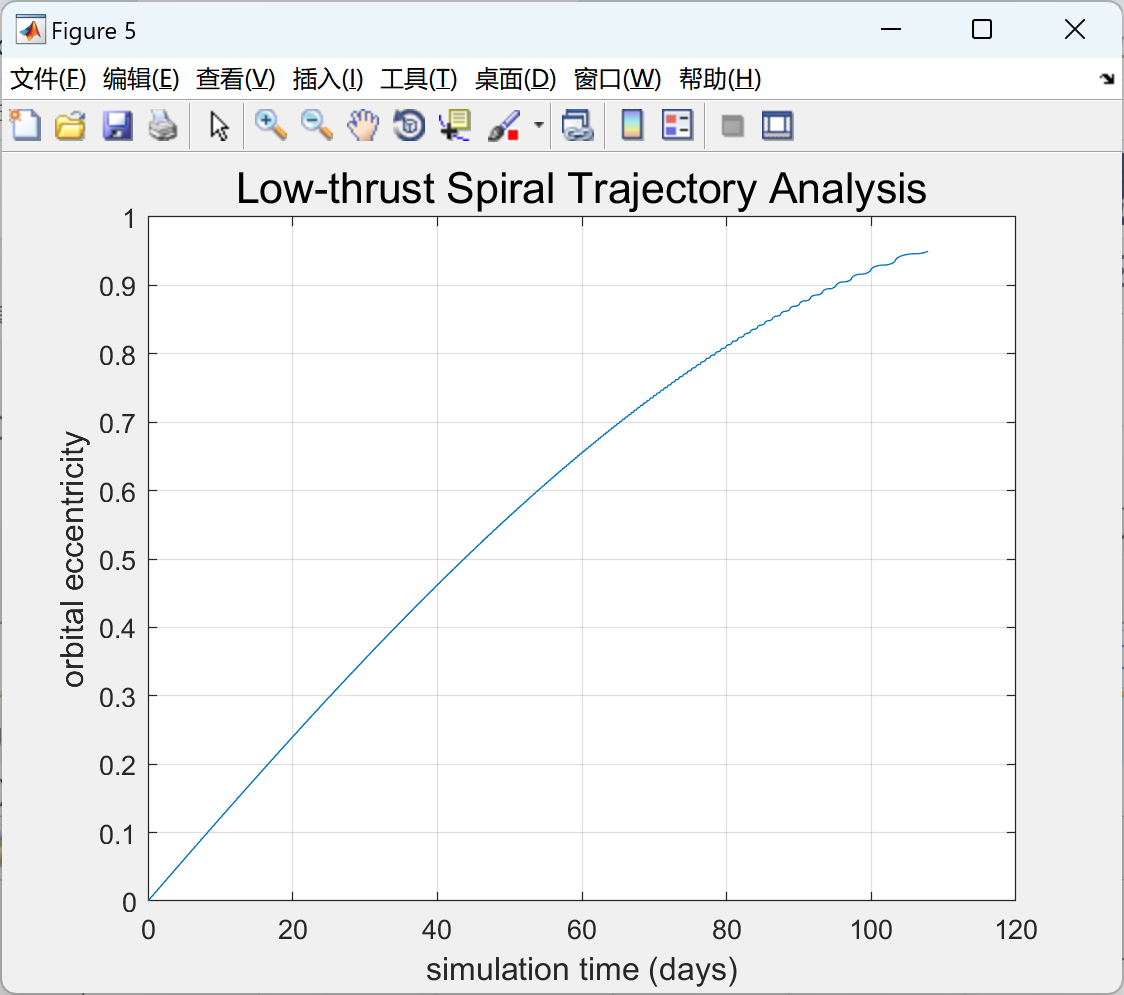
部分代码:
function [r, v, smovrp, cosl, sinl, wmee, ssqrd] = mee2eci_lts(mu, mee)
% convert modified equinoctial orbital elements to eci position
% and velocity vectors and auxillary variables
% input
% mu = gravitational constant (km**3/sec**2)
% mee(1) = semilatus rectum of orbit (kilometers)
% mee(2) = f equinoctial element
% mee(3) = g equinoctial element
% mee(4) = h equinoctial element
% mee(5) = k equinoctial element
% mee(6) = true longitude (radians)
% output
% r = eci position vector (kilometers)
% v = eci velocity vector (kilometers/second)
% auxilliary output quantities
% smovrp = sqrt(mu / pmee)
% cosl = cos(xlmee)
% sinl = sin(xlmee)
% wmee = 1.0 + fmee * cosl + gmee * sinl
% ssqrd = 1.0 + tani2s
% Orbital Mechanics with Matlab
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% unload equinoctial orbital elements
pmee = mee(1);
fmee = mee(2);
gmee = mee(3);
hmee = mee(4);
xkmee = mee(5);
xlmee = mee(6);
smovrp = sqrt(mu / pmee);
tani2s = hmee^2 + xkmee^2;
cosl = cos(xlmee);
sinl = sin(xlmee);
wmee = 1.0 + fmee * cosl + gmee * sinl;
radius = pmee / wmee;
hsmks = hmee^2 - xkmee^2;
ssqrd = 1.0 + tani2s;
% compute eci position vector (kilometers)
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]刘玥.火星探测器近心点制动与轨道保持优化设计[D].哈尔滨工业大学,2011.DOI:10.7666/d.D262275.
[2]夏勇俊.具有中心导体轴的螺旋槽慢波系统及注—波互作用的研究[D].电子科技大学[2023-08-27].DOI:CNKI:CDMD:2.2002.102390.
🌈4 Matlab代码实现
相关文章:

用于设计和分析具有恒定近心点半径的低推力螺旋轨迹研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

MongoDB - 构造复杂查询条件执行查询
文章目录 1. 构造 keyword 的查询条件2. 构造 threatSubType 的查询条件3. 相应的实体类 /*** 查询白名单详情** param offset 第几页开始* param limit 每页显示的最大值* param keyword 模糊搜索值* param order 排序方式(升序/降序…...

如何从ChatGPT中获得最佳聊天对话效果
从了解ChatGPT工作原理开始,然后从互动中学习,这是一位AI研究员的建议。 人们利用ChatGPT来撰写文章、论文、生成文案和计算机代码,或者仅仅作为学习或研究工具。然而,大多数人不了解它的工作原理或它能做什么,所以他…...

深入浅出:手把手教你实现单链表
一、什么是链表 链表是一种链状数据结构。简单来说,要存储的数据在内存中分别独立存放,它们之间通过某种方式相互关联。 如果我们使用C语言来实现链表,需要声明一个结构体作为链表的结点,结点之间使用指针关联。 二、单向链表的结…...

vite 打包项目后访问显示空白页的问题,开发环境正常,生产环境无报错。
有没有可能, 你跟我遇到同样的问题 白屏的写法 const routes [{path: /,component: import(../views/index.vue),} ]正确的写法 const routes [{path: /,component: () > import(../views/index.vue),} ]有时候方向很重要,当在错误的方向上无脑冲…...
打造成功的砍价营销大解析,销量飙升
砍价活动是吸引顾客的一种有效方式,可以帮助提高销量和提升品牌知名度。在乔拓云平台上,我们提供了一套简单易用的工具,让您能够轻松地制作一个成功的砍价活动。下面,我将详细介绍具体步骤,让您能够轻松上手。 第一步&…...

【Flink进阶】- Flink kubernetes operator 常用的命令
目录 1、应用程序管理 (1)提交 Flink 应用程序 (2)查看 Flink 应用程序列表...

ASP.NET Core 的日志系统
ASP.NET Core 提供了丰富日志系统。 可以通过多种途径输出日志,以满足不同的场景,内置的几个日志系统包括: Console,输出到控制台,用于调试,在产品环境可能会影响性能。Debug,输出到 System.Di…...
 以太网设置工具类)
android13(T) 以太网设置工具类
13 版本的以太网设置和以前版本有所变动,在 AS 中就能直接调用对应 API 将 build.gradle 版本修改 compileSdkVersion 31, 即可直接调用 EthernetManager 相关, 设置静态等方法可以通过反射调用设置。 以下是核心设置静态和动态参数工具类,…...

电脑报错提示xinput1_3.dll缺失怎么办?xinput1_3.dll丢失的简单恢复方案
今天,我将为大家分享一个与我们日常工作息息相关的话题——xinput1_3.dll丢失的4种解决方法。在我们的日常工作和生活中,电脑出现问题是常有的事,而xinput1_3.dll丢失则是其中较为常见的一种问题。那么,什么是xinput1_3.dll?它为…...

unity 之参数类型之引用类型
文章目录 引用类型引用类型与值类型的差异 引用类型 在Unity中,引用类型是指那些在内存中存储对象引用的数据类型。以下是在Unity中常见的引用类型的介绍: 节点(GameObject): 在Unity中,游戏对象ÿ…...
SpringBoot自定义工具类—基于定时器完成文件清理功能
直接复制粘贴既可!! import org.springframework.scheduling.annotation.Scheduled; import org.springframework.stereotype.Component; import java.io.File; import java.time.LocalDate; import java.time.LocalDateTime; import java.time.ZoneOff…...

安卓设置混淆后,gson报错解决方法
一,设置开启混淆release {minifyEnabled truezipAlignEnabled trueshrinkResources trueproguardFiles getDefaultProguardFile(proguard-android-optimize.txt), proguard-rules.pro } 二,混淆的文件中,对gson相关类不进行混淆,否…...
WPF实战项目十四(API篇):登录注册接口
1、新建UserDto.cs public class UserDto : BaseDto{private string userName;/// <summary>/// 用户名/// </summary>public string UserName{get { return userName; }set { userName value;OnPropertyChanged(); }}private string account;/// <summary>…...
10个免费PPT下载资源网站分享
PPT超级市场https://pptsupermarket.com/ PPT超级市场是一个完全免费的PPT模板下载网站,不需要注册登录,点击下载就能直接使用。 叮当设计https://www.dingdangsheji.com/ 叮当设计是一个完全免费的PPT模板下载网站,每一套PPT的质量都很高。除…...
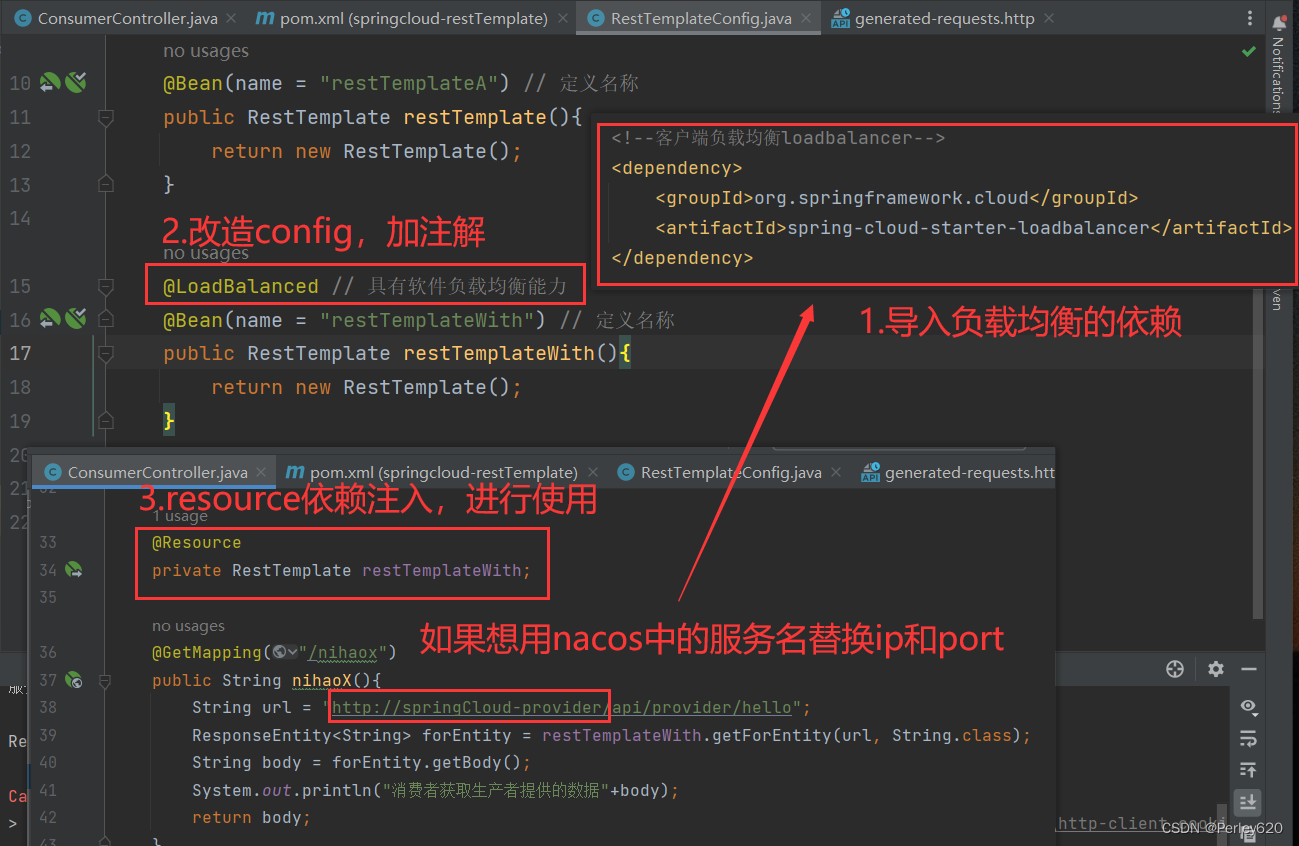
SpringCloud入门——微服务调用的方式 RestTemplate的使用 使用nacos的服务名初步(Ribbon负载均衡)
目录 引出微服务之间的调用几种调用方法spring提供的组件 RestTemplate的使用导入依赖生产者模块单个配置的情况多个配置的情况没加.yaml的报错【报错】两个同名配置【细节】 完整代码config配置主启动类controller层 消费者模块进行配置restTemplate配置类controller层 使用na…...
:python中__new__方法)
Python基础篇(16):python中__new__方法
一、__new__方法的定义 __new__() 方法是一种负责创建 类实例 的 静态方法 二、__new__方法的作用 在内存中为对象分配空间返回对象的引用 三、__new__方法的使用 创建对象时自动调用__new__方法,并且是在__init__初始化方法之前被调用Python解释器获得对象的引…...

linux并发服务器 —— 文件IO相关函数(三)
文件IO 以内存为主体,看待输入输出; 标准C库IO函数带有缓冲区,效率较高; 虚拟地址空间 虚拟地址空间是不存在的,一个应用程序运行期间对应一个虚拟地址空间; 虚拟地址空间的大小由CPU决定,位…...
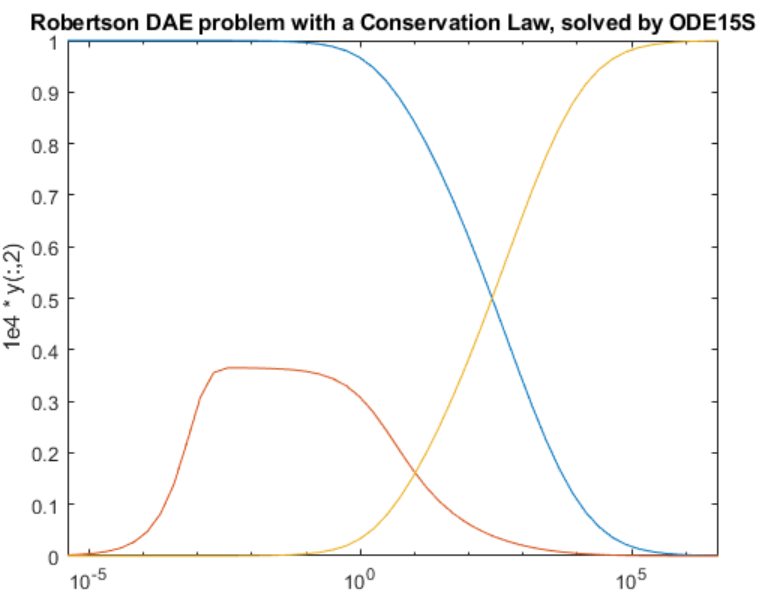
matlab使用教程(27)—微分代数方程(DAE)求解
1.什么是微分代数方程? 微分代数方程是一类微分方程,其中一个或多个因变量导数未出现在方程中。方程中出现的未包含其导数的变量称为代数变量,代数变量的存在意味着您不能将这些方程记为显式形式 y ′ f t , y 。相反,您可以…...

vue3组合式api <script setup> props 父子组件的写法
父组件传入子组个的变量, 子组件是无法直接修改的, 只能通过 emit的方式, 让父组件修改, 之后子组件更新 <template><div class"parent">我是父组件<son :msg"msg" :obj"obj" chan…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

