matlab使用教程(27)—微分代数方程(DAE)求解
1.什么是微分代数方程?

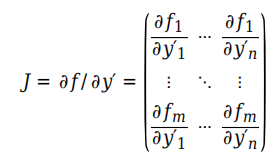
2.一致的初始条件
3.微分指数
4.施加非负性
5.将 Robertson 问题作为半显式微分代数方程 (DAE) 求解
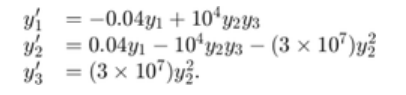
在解和初始条件方面,守恒定律为
![]()
通过使用守恒定律确定y3的状态,该方程组可以重写为 DAE 方程组。这会将问题重新表示为 DAE 方程组
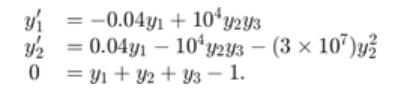
function out = robertsdae(t,y)
out = [-0.04*y(1) + 1e4*y(2).*y(3)
0.04*y(1) - 1e4*y(2).*y(3) - 3e7*y(2).^2
y(1) + y(2) + y(3) - 1 ];
y0 = [1; 0; 0];
tspan = [0 4*logspace(-6,6)];
M = [1 0 0; 0 1 0; 0 0 0];
options = odeset('Mass',M,'RelTol',1e-4,'AbsTol',[1e-6 1e-10 1e-6]);
[t,y] = ode15s(@robertsdae,tspan,y0,options);
y(:,2) = 1e4*y(:,2);
semilogx(t,y);
ylabel('1e4 * y(:,2)');
title('Robertson DAE problem with a Conservation Law, solved by ODE15S');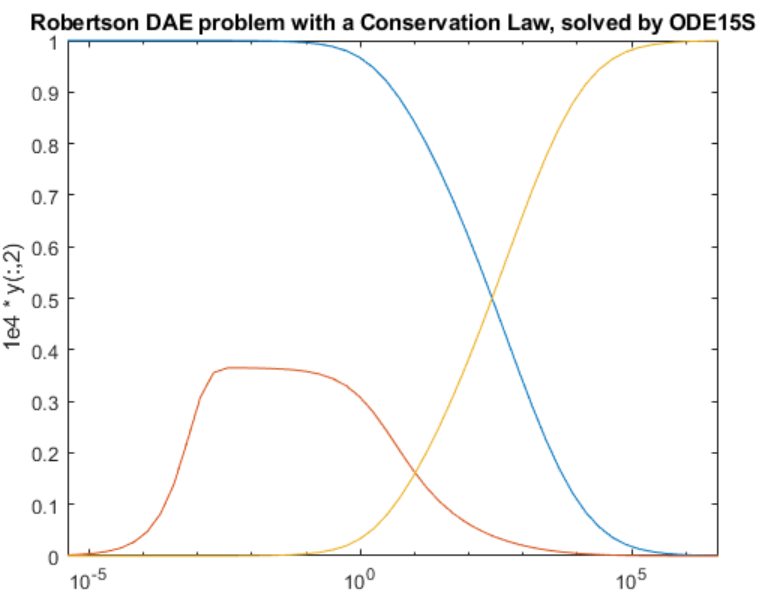
相关文章:

matlab使用教程(27)—微分代数方程(DAE)求解
1.什么是微分代数方程? 微分代数方程是一类微分方程,其中一个或多个因变量导数未出现在方程中。方程中出现的未包含其导数的变量称为代数变量,代数变量的存在意味着您不能将这些方程记为显式形式 y ′ f t , y 。相反,您可以…...

vue3组合式api <script setup> props 父子组件的写法
父组件传入子组个的变量, 子组件是无法直接修改的, 只能通过 emit的方式, 让父组件修改, 之后子组件更新 <template><div class"parent">我是父组件<son :msg"msg" :obj"obj" chan…...

Compose - 自定义作用域限制函数
一、概念 在 Compose 中对于作用域的应用特别多。比如 weight 修饰符只能用在 RowScope 或者 ColumnScope 作用域中,item 组件只能用在 LazyListScope 作用域中。 标准库中的作用域函数如 apply()、let() 会以不同方式持有和返回上下文对象,调用它们时 L…...
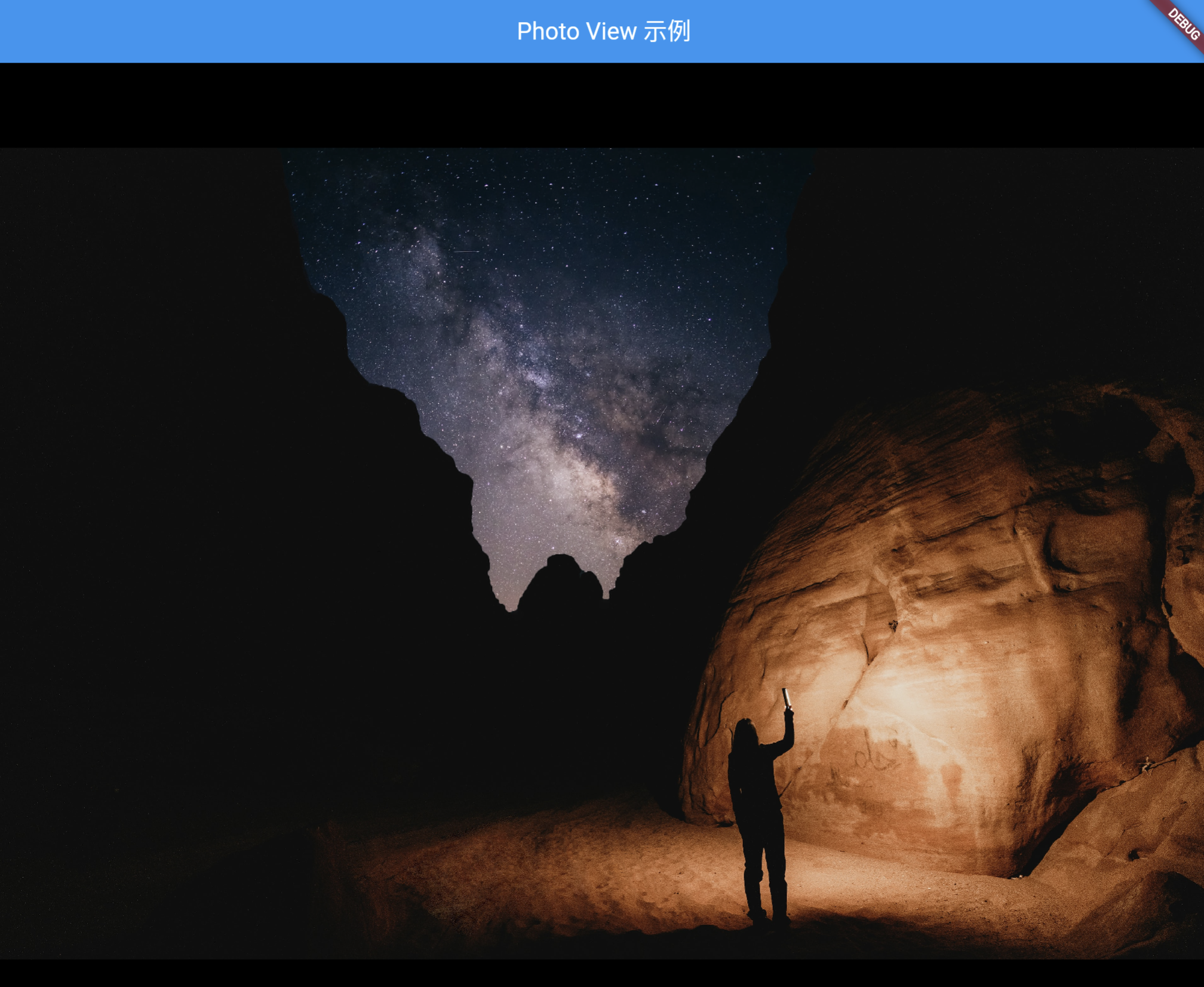
【Flutter】Flutter 使用 photo_view 实现图片查看器
【Flutter】Flutter 使用 photo_view 实现图片查看器 文章目录 一、前言二、photo_view 简介三、安装与基本使用四、使用 PhotoViewGallery 展示多张图片五、完整示例六、总结 一、前言 大家好,我是小雨青年,今天我要给大家介绍一个在 Flutter 中非常实…...

电脑组装教程分享!
案例:如何自己组装电脑? 【看到身边的小伙伴组装一台自己的电脑,我也想试试。但是我对电脑并不是很熟悉,不太了解具体的电脑组装步骤,求一份详细的教程!】 电脑已经成为我们日常生活中不可或缺的一部分&a…...
【云原生之Docker实战】使用Docker部署flatnotes笔记工具
【云原生之Docker实战】使用Docker部署flatnotes笔记工具 一、flatnotes介绍1.1 flatnotes简介1.2 flatnotes特点 二、本地环境介绍2.1 本地环境规划2.2 本次实践介绍 三、本地环境检查3.1 检查Docker服务状态3.2 检查Docker版本3.3 检查docker compose 版本 四、下载flatnotes…...
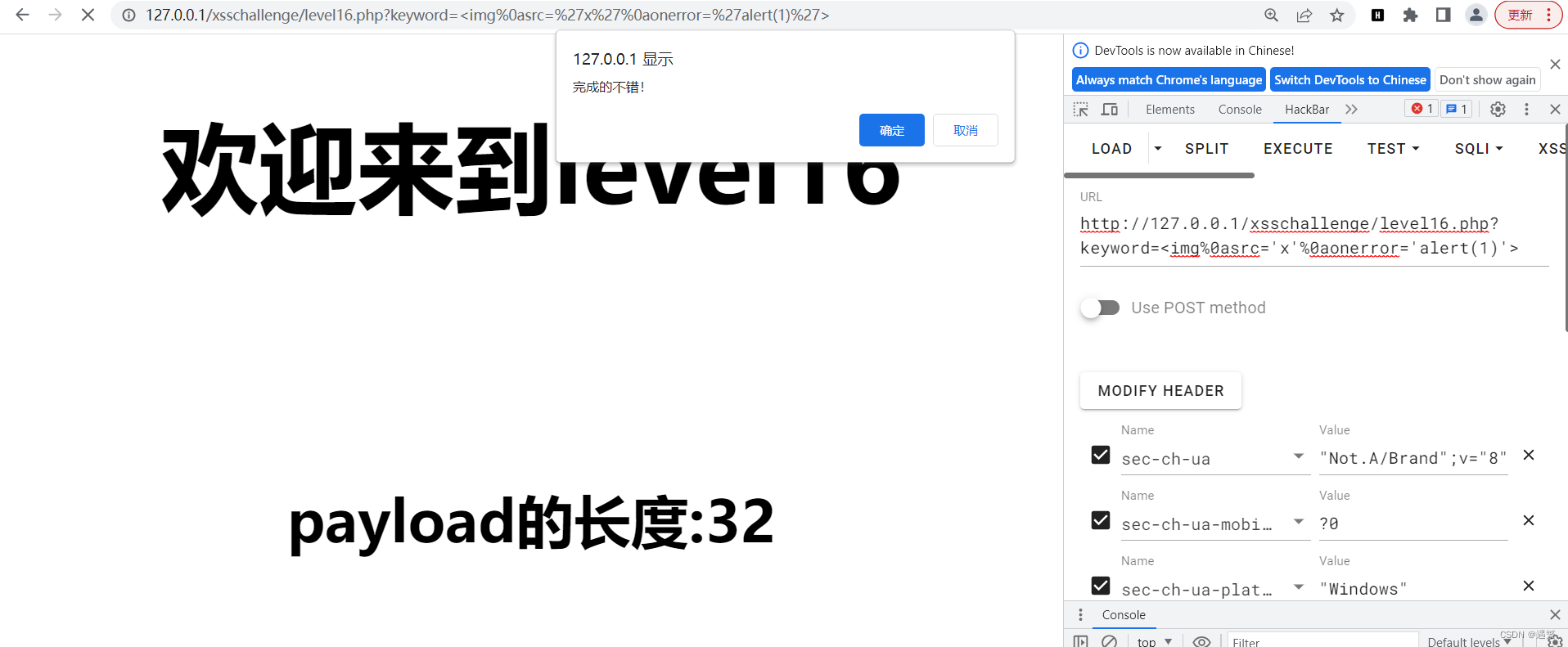
XSSchallenge1-20
test1 第一题直接在test插入XSS代码即可 test2 第二关对内容进行”“包裹 这里可以采用”>来绕过 test3 代码审计发现这里用了htmlspecialchars函数,这个函数对<>和’ “等进行了转义,这里可以用事件来绕过 test4 这里用了str_replace&a…...
centos 7的超详细安装教程
打开虚拟机,创建一个新电脑 我们选择经典,然后选择下一步 我们选择稍后安装,我们在后面进行改设备 因为centos系统是linux系统的一个版本,所有我们选择linux,版本选择centos 7 64位,然后就是点击下一步 这一…...
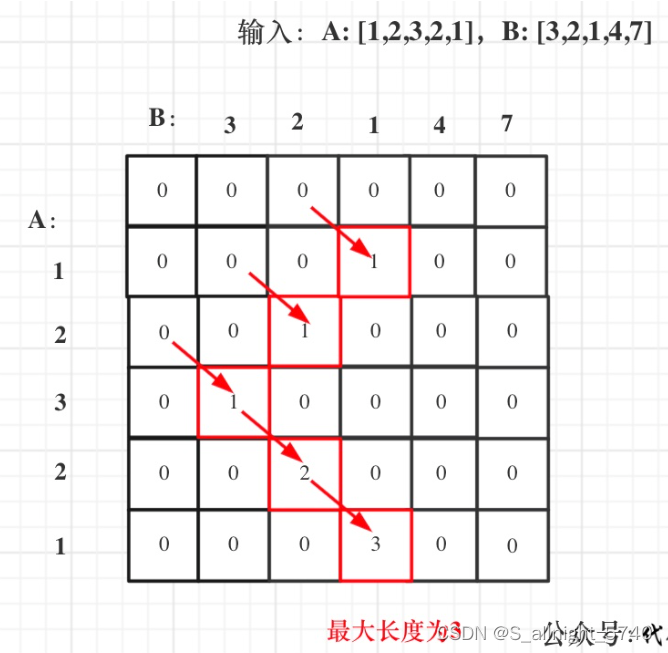
代码随想录算法训练营第五十二天 | 300.最长递增子序列,674. 最长连续递增序列,718. 最长重复子数组
代码随想录算法训练营第五十二天 | 300.最长递增子序列,674. 最长连续递增序列,718. 最长重复子数组 300.最长递增子序列674. 最长连续递增序列718. 最长重复子数组 300.最长递增子序列 题目链接 视频讲解 给你一个整数数组 nums ,找到其中最…...
6-6 小结)
计算机图形软件(三)6-6 小结
小结 这一章概括了图形软件系统的主要特点。某些软件系统,如 CAD 软件包和绘图程序,其为特定应用而设计。另外一些软件系统则提供可以在诸如 C的程序设计语言中使用的一个通用图形子程序库,用来为任何应用生成图片。 ISO和AN…...

Flink常用函数
1、比较函数 <> > > < < 注意:select nullnull; 返回为nullIS NULL 、 IS NOT NULL --非空判断value1 IS DISTINCT FROM value2、value1 IS NOT DISTINCT FROM value2、 --不同于value1 BETWEEN [ ASYMMETRIC | S OR 、AND、NOT boolean…...

stable diffusion实践操作-embedding(TEXTUAL INVERSION)
本文专门开一节写图生图相关的内容,在看之前,可以同步关注: stable diffusion实践操作 可以理解为提示词的集合,可以省略大量的提示词。后缀safetensors,大小几十kb 正文 1、功能 可以理解为提示词的集合࿰…...

代码随想录二刷day03
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣203. 移除链表元素二、力扣707. 设计链表三、力扣206. 反转链表 前言 一、力扣203. 移除链表元素 /*** Definition for singly-linked list.* public…...
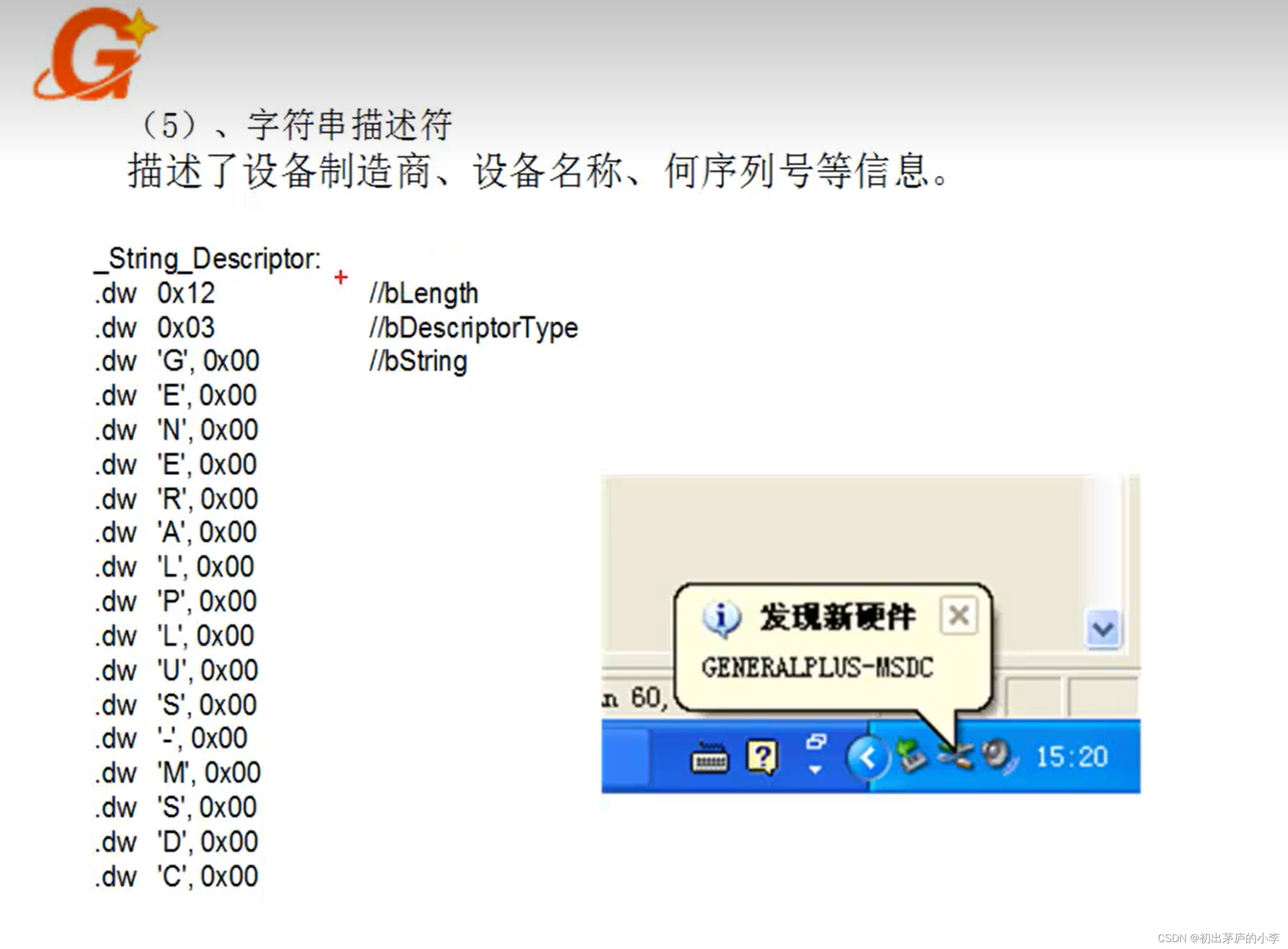
初出茅庐的小李博客之STM32F103C8T6音乐控制器实战教程【1】
STM32F103C8T6音乐控制器实战教程[1] USB简单介绍: "USB"代表通用串行总线(Universal Serial Bus),是一种用于连接计算机及其外部设备的标准接口。USB接口允许各种设备(如打印机、存储设备、键盘、鼠标、摄…...

苍穹外卖01-项目概述、环境搭建
项目概述、环境搭建 课程内容 软件开发整体介绍苍穹外卖项目介绍开发环境搭建导入接口文档Swagger 项目整体效果展示: 管理端-外卖商家使用用户端-点餐用户使用当我们完成该项目的学习,可以培养以下能力: 1. 软件开发整体介绍 作为一名软…...

图床项目进度(二)——动态酷炫首页
前言: 前面的文章我不是说我简单copy了站友的一个登录页吗,我感觉还是太单调了,想加一个好看的背景。 但是我前端的水平哪里够啊,于是在网上找了找制作动态背景的插件。 效果如下图。 如何使用 这个插件是particles.js 安装…...

Java“魂牵”京东商品详情描述数据,京东商品详情API接口,京东API接口申请指南
要通过京东的API获取商品详情描述数据,您可以使用京东开放平台提供的接口来实现。以下是一种使用Java编程语言实现的示例,展示如何通过京东开放平台API获取商品详情: 首先,确保您已注册成为京东开放平台的开发者,并创…...
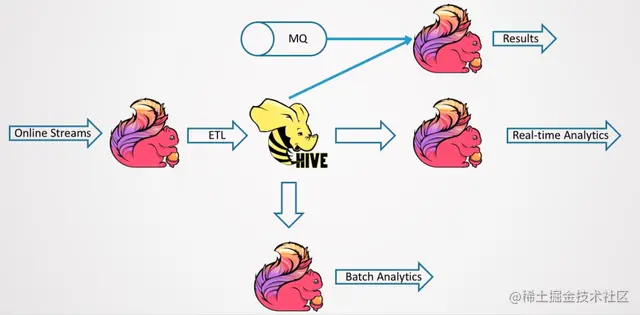
Flink SQL你用了吗?
分析&回答 Flink 1.1.0:第一次引入 SQL 模块,并且提供 TableAPI,当然,这时候的功能还非常有限。Flink 1.3.0:在 Streaming SQL 上支持了 Retractions,显著提高了 Streaming SQL 的易用性,使…...

【位运算】leetcode面试题:消失的两个数字
一.题目描述 消失的两个数字 二.思路分析 本题难度标签是困难,但实际上有了只出现一次的数字iii这道题的铺垫,本题的思路还是很容易想到的。 温馨提示:阅读本文前可以先查看我的【位运算】专栏的第一篇文章,其中包含位运算这类…...
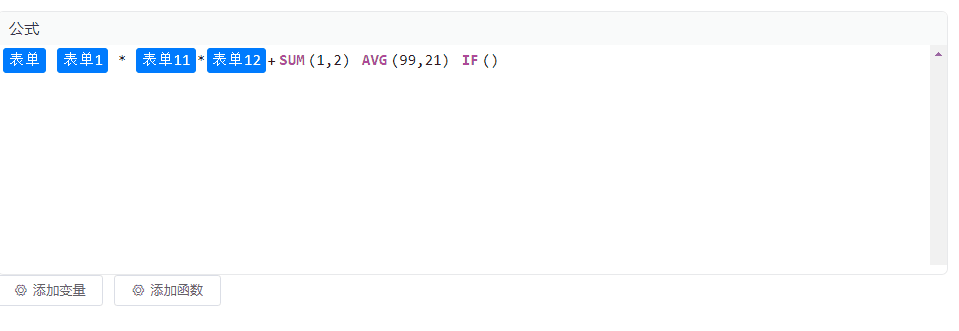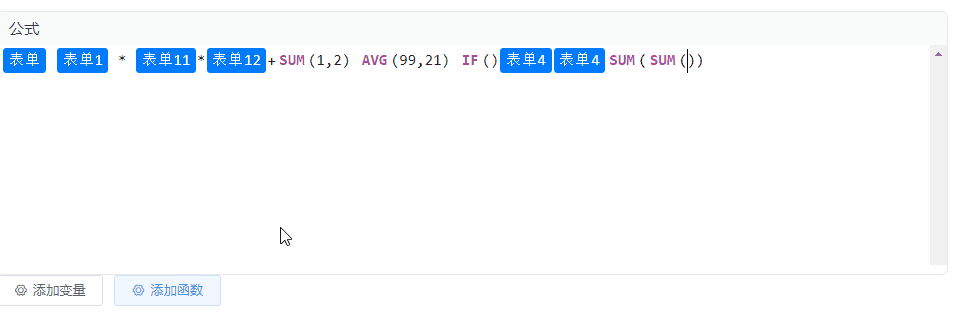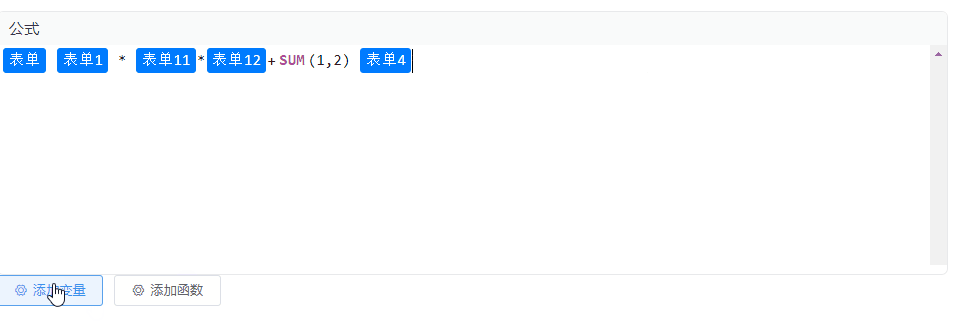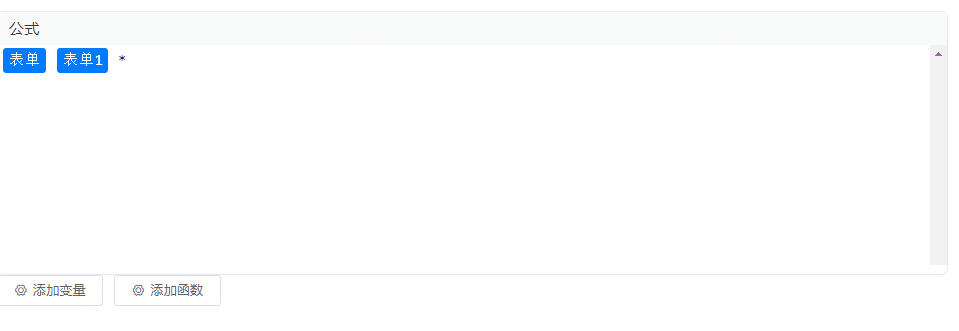
Vue2 集成 CodeMirror 实现公式编辑、块状文本编辑,TAG标签功能
效果图 安装codemirror依赖 本示例为Vue2项目,安装低版本的依赖 npm i codemirror5.65.12 npm i vue-codemirror4.0.6 实现 实现代码如下,里边涉及到的变量和函数自行替换即可,没有其他复杂逻辑。 <template><div class"p…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
