代码随想录算法训练营第五十二天 | 300.最长递增子序列,674. 最长连续递增序列,718. 最长重复子数组
代码随想录算法训练营第五十二天 | 300.最长递增子序列,674. 最长连续递增序列,718. 最长重复子数组
- 300.最长递增子序列
- 674. 最长连续递增序列
- 718. 最长重复子数组
300.最长递增子序列
题目链接
视频讲解
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度,子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序,例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
dp[i]的定义
本题中,正确定义dp数组的含义十分重要
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度,为什么一定表示 “以nums[i]结尾的最长递增子序” ,因为我们在 做 递增比较的时候,如果比较 nums[j] 和 nums[i] 的大小,那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾, 要不然这个比较就没有意义了,不是尾部元素的比较那么 如何算递增呢
状态转移方程
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值
所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
注意这里不是要dp[i] 与 dp[j] + 1进行比较,而是我们要取dp[j] + 1的最大值
dp[i]的初始化
每一个i,对应的dp[i](即最长递增子序列)起始大小至少都是1.
确定遍历顺序
dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来,那么遍历i一定是从前向后遍历
j其实就是遍历0到i-1,那么是从前到后,还是从后到前遍历都无所谓,只要吧 0 到 i-1 的元素都遍历了就行了
遍历i的循环在外层,遍历j则在内层,代码如下:
for (int i = 1; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);}if (dp[i] > result) result = dp[i]; // 取长的子序列
}
举例推导dp数组
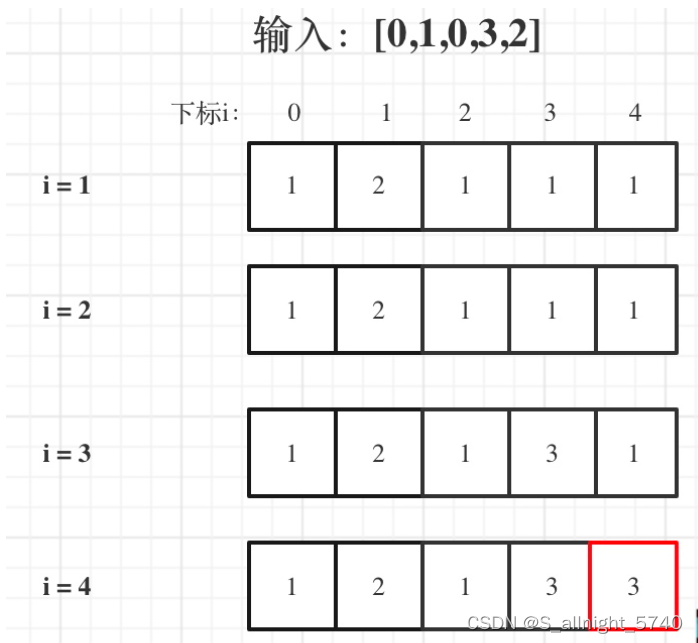
输入:[0,1,0,3,2],dp数组的变化如下:
class Solution {
public:int lengthOfLIS(vector<int>& nums) {if (nums.size() <= 1) return nums.size();vector<int> dp(nums.size(), 1);int result = 0;for (int i = 1; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);}if (dp[i] > result) result = dp[i]; // 取长的子序列}return result;}
};
674. 最长连续递增序列
题目链接
视频讲解
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度,连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列
输入:nums = [1,3,5,4,7]
输出:3
动规五部曲分析如下:
确定dp数组(dp table)以及下标的含义
dp[i]:以下标i为结尾的连续递增的子序列长度为dp[i]
注意这里的定义,一定是以下标i为结尾,并不是说一定以下标0为起始位置
确定递推公式
如果 nums[i] > nums[i - 1],那么以 i 为结尾的连续递增的子序列长度 一定等于 以i - 1为结尾的连续递增的子序列长度 + 1,即:dp[i] = dp[i - 1] + 1;
因为本题要求连续递增子序列,所以就只要比较nums[i]与nums[i - 1],而不用去比较nums[j]与nums[i] (j是在0到i之间遍历)既然不用j了,那么也不用两层for循环,本题一层for循环就行,比较nums[i] 和 nums[i - 1]
dp数组如何初始化
以下标i为结尾的连续递增的子序列长度最少也应该是1,即就是nums[i]这一个元素
所以dp[i]应该初始1;
确定遍历顺序
从递推公式上可以看出, dp[i + 1]依赖dp[i],所以一定是从前向后遍历
本文在确定递推公式的时候也说明了为什么本题只需要一层for循环,代码如下:
for (int i = 1; i < nums.size(); i++) {if (nums[i] > nums[i - 1]) { // 连续记录dp[i] = dp[i - 1] + 1;}
}
举例推导dp数组
已输入nums = [1,3,5,4,7]为例,dp数组状态如下:
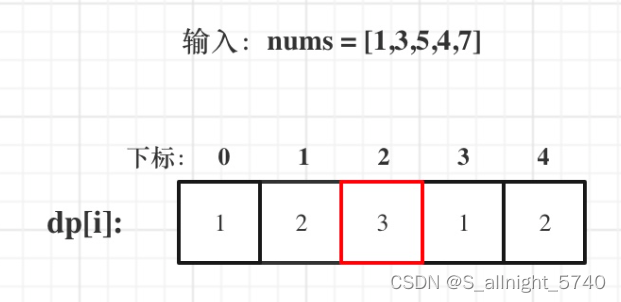
注意这里要取dp[i]里的最大值,所以dp[2]才是结果!
class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {if (nums.size() == 0) return 0;int result = 1;vector<int> dp(nums.size() ,1);for (int i = 1; i < nums.size(); i++) {if (nums[i] > nums[i - 1]) { // 连续记录dp[i] = dp[i - 1] + 1;}if (dp[i] > result) result = dp[i];}return result;}
};
718. 最长重复子数组
题目链接
视频讲解
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
确定dp数组(dp table)以及下标的含义
dp[i][j] :以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]。 (特别注意: “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 )那dp[0][0]是什么含义呢?总不能是以下标-1为结尾的A数组吧,其实dp[i][j]的定义也就决定着,我们在遍历dp[i][j]的时候i 和 j都要从1开始
那有人问了,定义dp[i][j]为 以下标i为结尾的A,和以下标j 为结尾的B,最长重复子数组长度。不行么?行倒是行! 但实现起来就麻烦一点,需要单独处理初始化部分,在本题解下面的拓展内容里,我给出了 第二种 dp数组的定义方式所对应的代码和讲解,大家比较一下就了解了
确定递推公式
根据dp[i][j]的定义,dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来
即当A[i - 1] 和B[j - 1]相等的时候,dp[i][j] = dp[i - 1][j - 1] + 1;
根据递推公式可以看出,遍历i 和 j 要从1开始!
dp数组如何初始化
根据dp[i][j]的定义,dp[i][0] 和dp[0][j]其实都是没有意义的!
但dp[i][0] 和dp[0][j]要初始值,因为 为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;
所以dp[i][0] 和dp[0][j]初始化为0
举个例子A[0]如果和B[0]相同的话,dp[1][1] = dp[0][0] + 1,只有dp[0][0]初始为0,正好符合递推公式逐步累加起来
确定遍历顺序
外层for循环遍历A,内层for循环遍历B
同时题目要求长度最长的子数组的长度,所以在遍历的时候顺便把dp[i][j]的最大值记录下来
代码如下:
for (int i = 1; i <= nums1.size(); i++) {for (int j = 1; j <= nums2.size(); j++) {if (nums1[i - 1] == nums2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;}if (dp[i][j] > result) result = dp[i][j];}
}
举例推导dp数组
拿示例1中,A: [1,2,3,2,1],B: [3,2,1,4,7]为例,画一个dp数组的状态变化,如下:
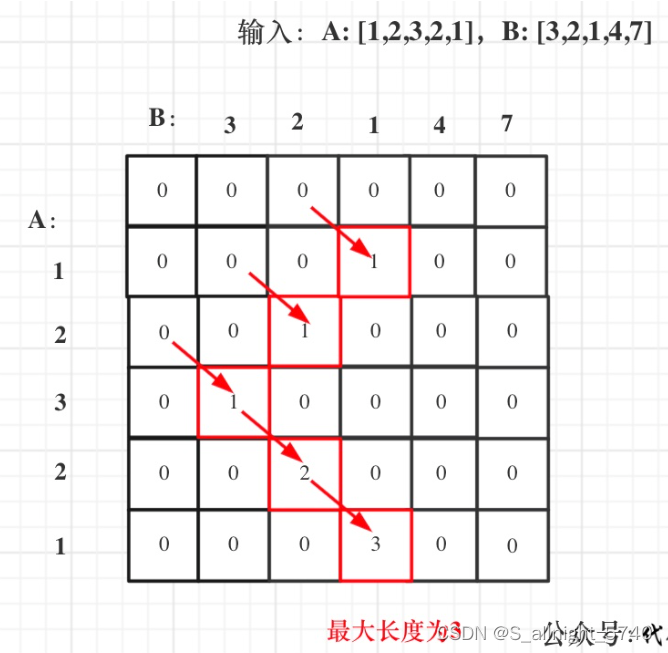
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));int result = 0;for (int i = 1; i <= nums1.size(); i++) {for (int j = 1; j <= nums2.size(); j++) {if (nums1[i - 1] == nums2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;}if (dp[i][j] > result) result = dp[i][j];}}return result;}
};
相关文章:

代码随想录算法训练营第五十二天 | 300.最长递增子序列,674. 最长连续递增序列,718. 最长重复子数组
代码随想录算法训练营第五十二天 | 300.最长递增子序列,674. 最长连续递增序列,718. 最长重复子数组 300.最长递增子序列674. 最长连续递增序列718. 最长重复子数组 300.最长递增子序列 题目链接 视频讲解 给你一个整数数组 nums ,找到其中最…...
6-6 小结)
计算机图形软件(三)6-6 小结
小结 这一章概括了图形软件系统的主要特点。某些软件系统,如 CAD 软件包和绘图程序,其为特定应用而设计。另外一些软件系统则提供可以在诸如 C的程序设计语言中使用的一个通用图形子程序库,用来为任何应用生成图片。 ISO和AN…...

Flink常用函数
1、比较函数 <> > > < < 注意:select nullnull; 返回为nullIS NULL 、 IS NOT NULL --非空判断value1 IS DISTINCT FROM value2、value1 IS NOT DISTINCT FROM value2、 --不同于value1 BETWEEN [ ASYMMETRIC | S OR 、AND、NOT boolean…...

stable diffusion实践操作-embedding(TEXTUAL INVERSION)
本文专门开一节写图生图相关的内容,在看之前,可以同步关注: stable diffusion实践操作 可以理解为提示词的集合,可以省略大量的提示词。后缀safetensors,大小几十kb 正文 1、功能 可以理解为提示词的集合࿰…...

代码随想录二刷day03
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣203. 移除链表元素二、力扣707. 设计链表三、力扣206. 反转链表 前言 一、力扣203. 移除链表元素 /*** Definition for singly-linked list.* public…...
初出茅庐的小李博客之STM32F103C8T6音乐控制器实战教程【1】
STM32F103C8T6音乐控制器实战教程[1] USB简单介绍: "USB"代表通用串行总线(Universal Serial Bus),是一种用于连接计算机及其外部设备的标准接口。USB接口允许各种设备(如打印机、存储设备、键盘、鼠标、摄…...

苍穹外卖01-项目概述、环境搭建
项目概述、环境搭建 课程内容 软件开发整体介绍苍穹外卖项目介绍开发环境搭建导入接口文档Swagger 项目整体效果展示: 管理端-外卖商家使用用户端-点餐用户使用当我们完成该项目的学习,可以培养以下能力: 1. 软件开发整体介绍 作为一名软…...

图床项目进度(二)——动态酷炫首页
前言: 前面的文章我不是说我简单copy了站友的一个登录页吗,我感觉还是太单调了,想加一个好看的背景。 但是我前端的水平哪里够啊,于是在网上找了找制作动态背景的插件。 效果如下图。 如何使用 这个插件是particles.js 安装…...

Java“魂牵”京东商品详情描述数据,京东商品详情API接口,京东API接口申请指南
要通过京东的API获取商品详情描述数据,您可以使用京东开放平台提供的接口来实现。以下是一种使用Java编程语言实现的示例,展示如何通过京东开放平台API获取商品详情: 首先,确保您已注册成为京东开放平台的开发者,并创…...
Flink SQL你用了吗?
分析&回答 Flink 1.1.0:第一次引入 SQL 模块,并且提供 TableAPI,当然,这时候的功能还非常有限。Flink 1.3.0:在 Streaming SQL 上支持了 Retractions,显著提高了 Streaming SQL 的易用性,使…...

【位运算】leetcode面试题:消失的两个数字
一.题目描述 消失的两个数字 二.思路分析 本题难度标签是困难,但实际上有了只出现一次的数字iii这道题的铺垫,本题的思路还是很容易想到的。 温馨提示:阅读本文前可以先查看我的【位运算】专栏的第一篇文章,其中包含位运算这类…...
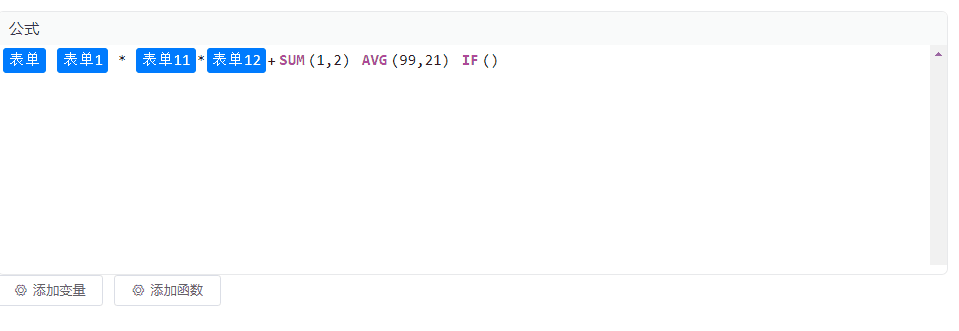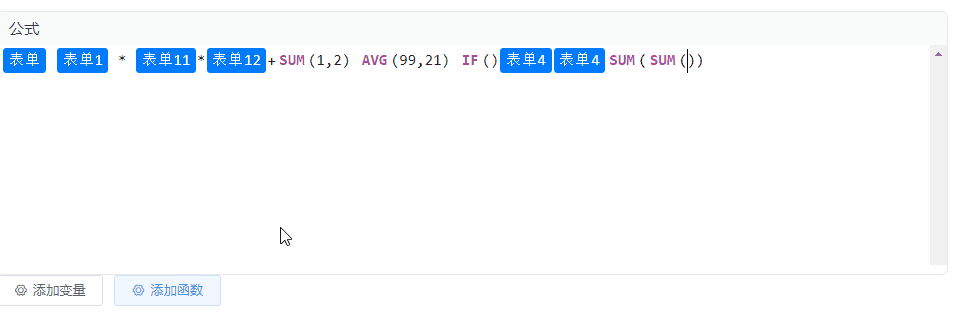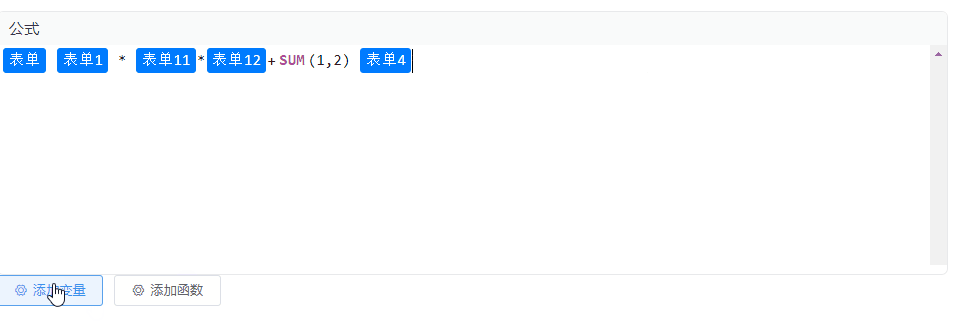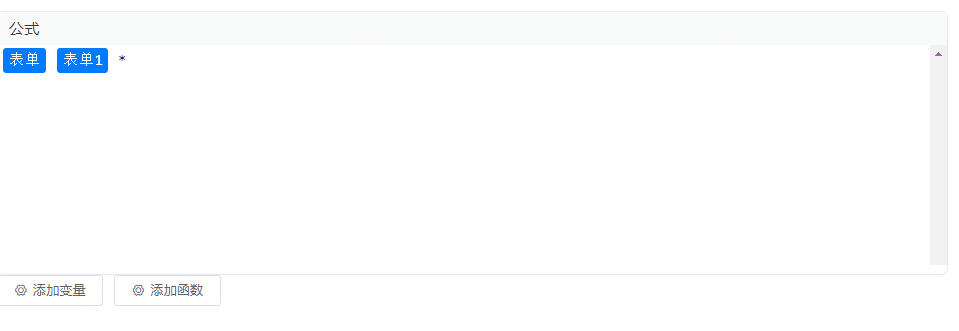
Vue2 集成 CodeMirror 实现公式编辑、块状文本编辑,TAG标签功能
效果图 安装codemirror依赖 本示例为Vue2项目,安装低版本的依赖 npm i codemirror5.65.12 npm i vue-codemirror4.0.6 实现 实现代码如下,里边涉及到的变量和函数自行替换即可,没有其他复杂逻辑。 <template><div class"p…...

CCF-CSP 30次 第二题【矩阵运算】
计算机软件能力认证考试系统 #include<bits/stdc.h> using namespace std; const int N1e410; #define int long long int n,d; int q[N][22],k[22][N],v[N][22],w[N]; int ans1[N][22],ans2[N][22]; signed main() {scanf("%lld %lld",&n,&d);for(in…...

最大子数组和【贪心算法】
最大子数组和 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 class Solution {public int maxSubArray(int[] nums) {//记录最大结果&…...

linux并发服务器 —— Makefile与GDB调试(二)
Makefile Makefile:定义规则指定文件的编译顺序;类似shell脚本,执行操作系统命令 优点:自动化编译——通过make(解释Makefile文件中指令的命令)命令完全编译整个工程,提高软件开发效率&#x…...
Ansible学习笔记14
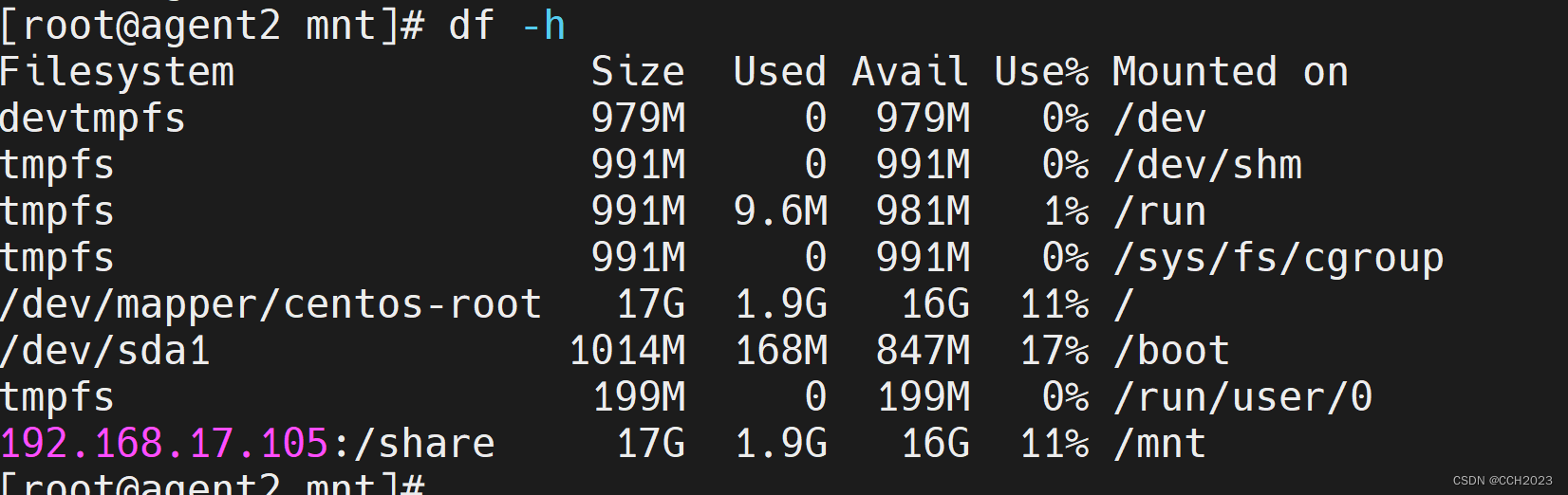
实现多台的分离实现: [rootlocalhost playbook]# cat example3.yaml --- - hosts: 192.168.17.105remote_user: roottasks:- name: create test1 directoryfile: path/test1/ statedirectory- hosts: 192.168.17.106remote_user: roottasks:- name: create test2 d…...

docker 安装 mysql 并挂载 配置文件和数据目录
1、宿主机创建挂载目录 sudo mkdir /path/mysql/data sudo mkdir /path/mysql/conf2、搜索镜像 docker search mysql拉取官方支持版本(OFFICIAL 为 ok的版本) docker pull mysql:latest3、以 mysql 作为基础镜像构建容器并挂载目录 docker run -d -p…...

代码随想录训练营 DP01
代码随想录训练营 DP01 509. 🌸斐波那契数🌸code 70. 🌸爬楼梯🌸code 746. 🌸使用最小花费爬楼梯🌸code 509. 🌸斐波那契数🌸 斐波那契数 (通常用 F(n) 表示)…...

github+hexo 博客搭建
文章目录 1.安装Node.js、Git和Hexo2.创建 GitHub 仓库并配置ssh3.初始化Hexo4.配置Hexo5.创建博客内容6.部署7.查看8.参考:9.选择主题: 环境:win11wsl 1.安装Node.js、Git和Hexo 打开终端安装以下软件 sudo apt update sudo apt-get insta…...
)
Spring Security bug记录:antMatchers找不到符号(已解决)
目录 Spring Security bug记录:antMatchers找不到符号(已解决)原因:解决:参考链接: Spring Security bug记录:antMatchers找不到符号(已解决) 原因: 新版本…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
