连续时间信号与离散时间信号
前言
《信号与系统》是一门很难的课,也是许多学校考研要考的专业课,由于每周只有两节课,所以每次上完都要及时的去复习,这里参考的教材是奥本海姆著作,刘海棠译,北京:电子工业出版社,2013年。
信号类型的区分
-
确定信号与随机信号
确定信号:若被表示为一确定的时间函数,知道某一时间即可得知当前的信号信息。
随机信号:带有随机的特点,无法预测,不能用函数表示,只能用概率统计的方法描述的信号。
-
连续信号与离散信号
连续信号:连续时间范围内有定义的信号,自变量用t表示。
离散信号:在时间上表示离散,仅能用整数表示,自变量用n表示。 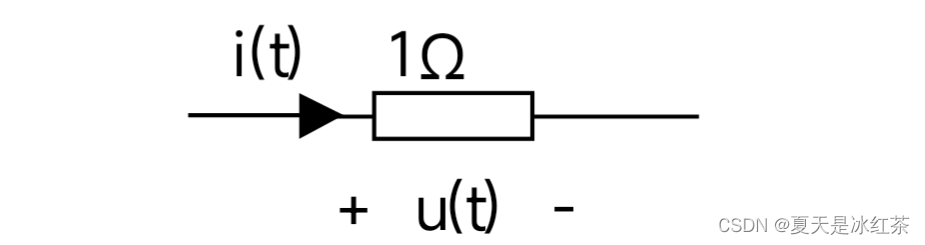
在连续信号的情况下,对于1欧姆的电阻上,不管是电压信号u(t)还是电流信号i(t),都将其定义为x(t),则其瞬间功率为。
能量:
若,
平均功率:
那么对于离散信号
能量:
平均功率:
-
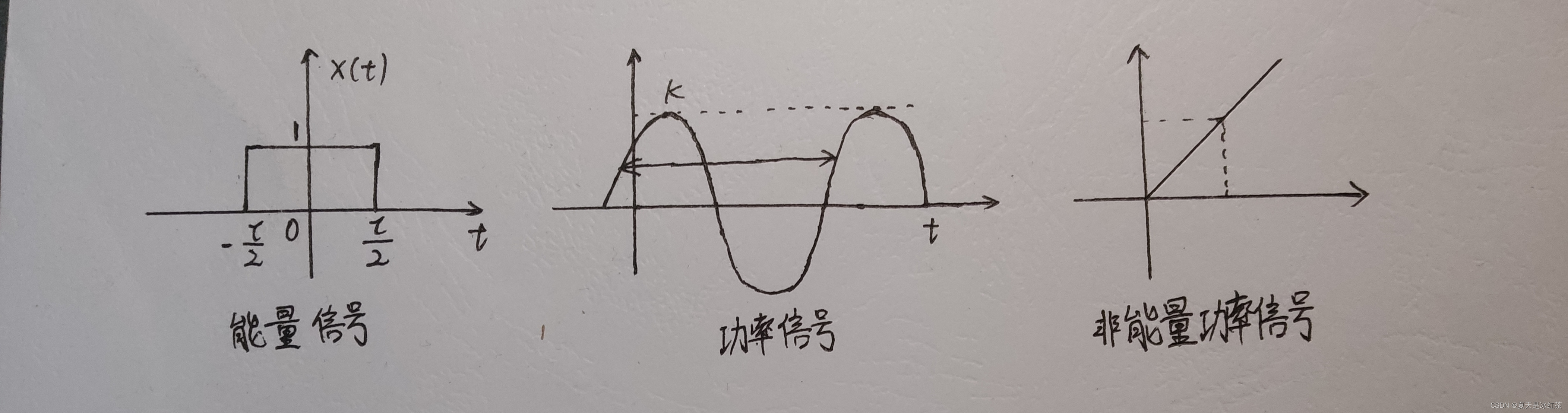
能量信号与功率信号
能量: 平均功率:
可以看出
若,则将x(t)或x[n]称为能量信号(
,E有界)。
若,则将x(t)或x[n]称为功率信号(
,P有界)。
可以这样理解,当信号具有有限的能量,即
,这种信号的平均功率必为0;第二种信号就是其平均功率
有限的信号,如果
,必有
,因为如果单位时间内有某一个非零的平均功率,在无限积分或求和就必然得出无限大的能量值。
第三类信号就是
和
都不是有限的。
如果这样说还是不能理解,那么就举些例子,比如信号在内为1,在此区间外为0就是有限能量信号的另一个例子,此时
,例如常数x[n]=4就具有无限能量,但是平均功率
,在看信号x(t)=t,
和
都不是有限的。
总结:它们有下面的这几种组合
有限能量+零功率---->能量信号
代表波形:孤零零的方波、极限值为0的波形
无穷能量+有限功率--->功率信号
代表波形:一个无限延伸的正弦波、无线长的白噪声
无穷能量+无穷功率--->非功非能信号
代表波形:无限延伸的单调波形
-
周期信号与非周期信号
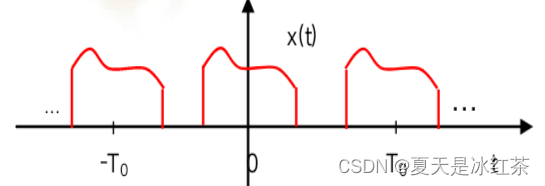
连续周期信号:一个连续信号x(t),若对所有t均有:x(t)=x(t+kT),k为整数。满足这个式子的最小周期为基波周期,用T0来表示。
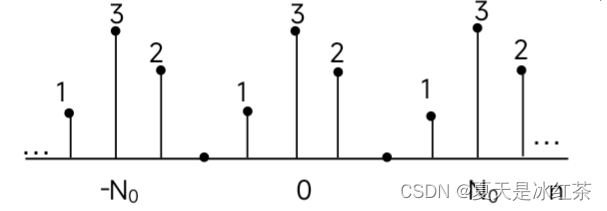
离散周期信号:一个离散信号x[n],若对所有n均有:x[n]=x[n+mN],m为整数。满足这个式子的最小周期为基波周期,用N0来表示。
-
连续时间和离散时间信号
对于信号的组合,它的周期性判断以及基波周期的求解:
(1)连续信号
,若
是有理数
则
是周期的,其基波周期:T0=LCM(
),LCM最小公倍数。
(2)离散信号
一定是周期的,其基波周期为:N0=LCM(
)。
相关文章:
连续时间信号与离散时间信号
前言 《信号与系统》是一门很难的课,也是许多学校考研要考的专业课,由于每周只有两节课,所以每次上完都要及时的去复习,这里参考的教材是奥本海姆著作,刘海棠译,北京:电子工业出版社࿰…...
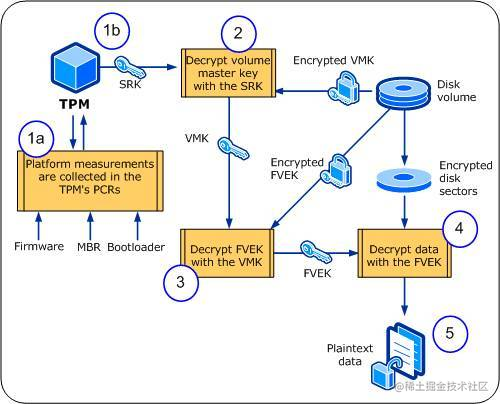
TPM密钥管理、使用
前面讲过证书相关内容,除了在软件方面有所应用外,在硬件方面也有很多应用。本次讲一下TPM相关的内容。 一、TPM介绍 1.1背景 TCG基于硬件安全的架构是为应对1990s后期日益增多的复杂恶意软件攻击应用而生的。当时以及现在,抵御PC客户端网络…...
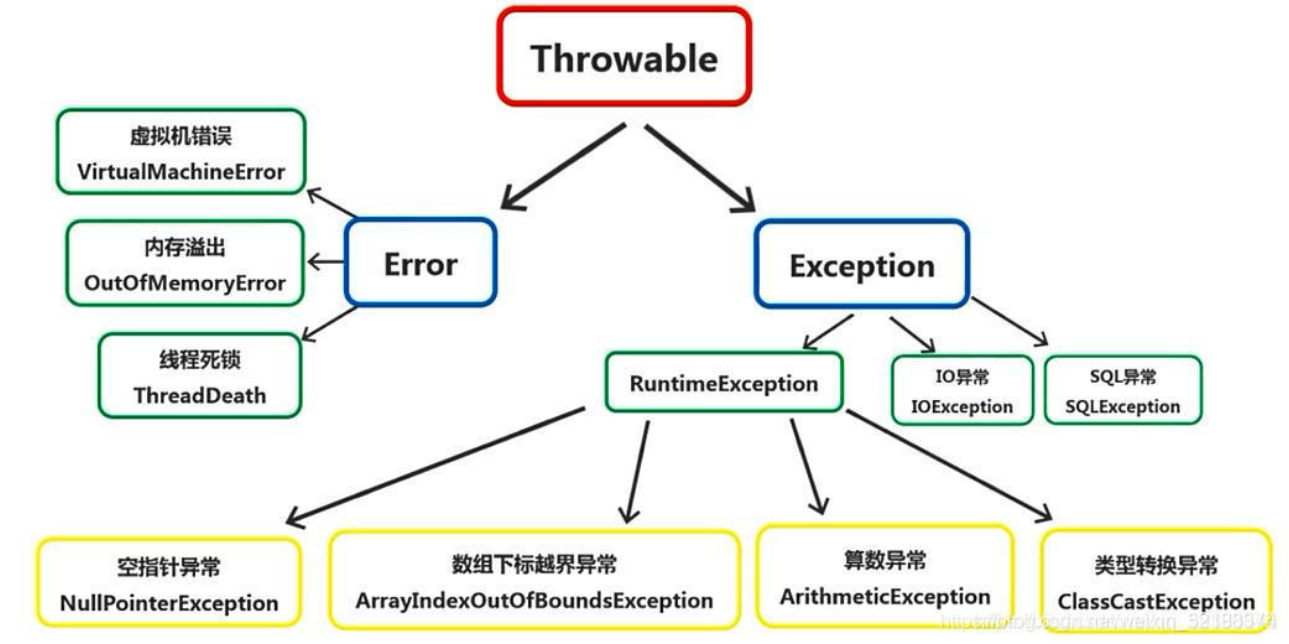
return和finally执行顺序、运行时异常与一般异常异同、error和exception区别、Java异常处理机制原理与应用
文章目录1.try {}里有一个return语句,那么紧跟在这个try后的finally{}里的code会不会被执行,什么时候被执行,在return前还是后?2.运行时异常与一般异常有何异同?3.java 程序中的错误有三种类型分别是什么4.error和exception有什么…...
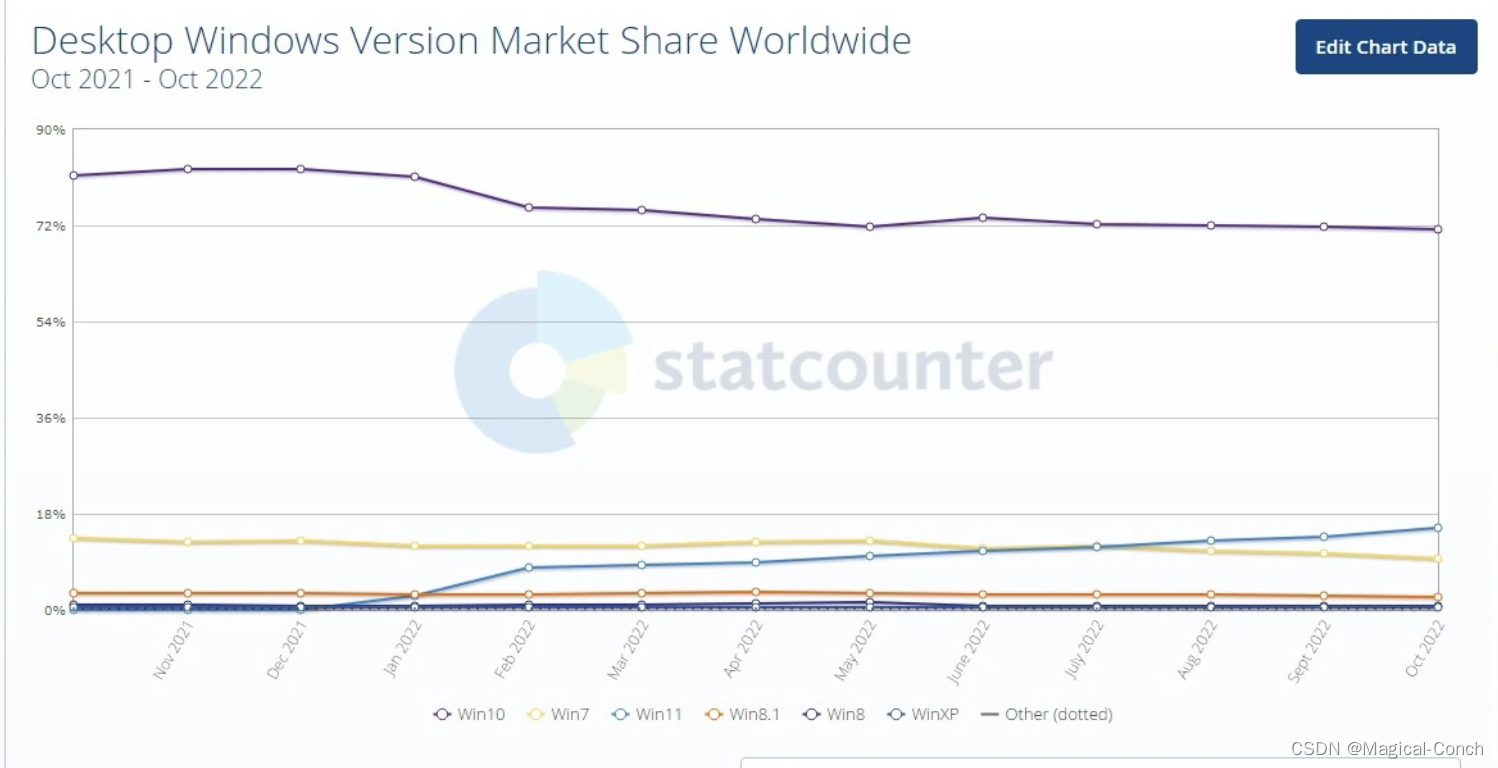
我为什么放弃WinUI3
基于WinUI3开发HiNote已经有一个多月的时间了,算是做出来一个简单能用的C端软件。 基于个人的经历,说说其中的开发体验。 UI设计语言 无论是否抄袭苹果,WinUI3给人的感觉都是眼前一亮的。简洁美观,现代化,毛玻璃的美…...

2023年全国最新安全员精选真题及答案2
百分百题库提供安全员考试试题、建筑安全员考试预测题、建筑安全员ABC考试真题、安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 21.(单选题)静作用压路机在施工过程,要求实际含水量…...
计算机408考研先导课---C语言难点
以下为小编在重温C语言时,容易犯错的一些点,希望列出来对大家有一定帮助! 一、整型变量数的范围 类型说明符长度(字节)数的范围int4/2(有些为4字节,有些为2字节)-32768~32767short2…...

K8S 部署 Redis-Cluster 集群
本文使用 bitnami 镜像部署 redis-cluster 官方文档:https://github.com/bitnami/charts/tree/main/bitnami/redis-cluster 添加 bitnami 仓库 helm repo add bitnami https://charts.bitnami.com/bitnami自定义 values.yaml storageClass:集群的存储…...

[oeasy]python0089_大型机的衰落_Dec小型机崛起_PDP_VAX网络
编码进化 回忆上次内容 上次 回顾了 计算机存储单位的演变 最小的读写单位 是 bit 8-bit 固定下来 成为了字节(Byte) 位数容量8-bit1Byte1024Byte1 KB1024 KB1 MB1024 MB1 GB1024 GB1 TB 存储字符时 第1位 是 标志位后7位 是 ascii具体的值 可以用 1Byte 存储 计算机之间 …...
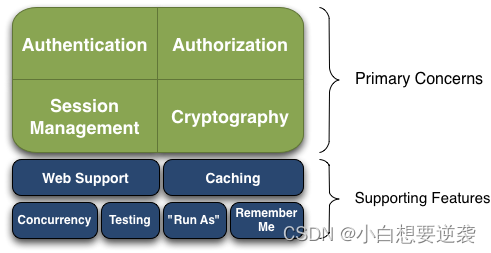
Apache Shiro与Spring Security对比
Apache Shiro VS Spring Security 1.Spring Security 官方文档:https://spring.io/projects/spring-security#overview介绍: Spring Security是一个能够为基于Spring的企业应用系统提供声明式的安全访问控制解决方案的安全框架。它提供了一组可以在Spr…...

23春招-mysql事务相关高频面试题
1、什么是事务 对于一个事务,要么事务内的sql全部执行,要么都不执行 2、 事务的特性ACID 原子性 整个事务中所有的操作要么全部提交成功,要么全部失败会滚。 一致性 数据库总是从一个一致性状态转换到另一个一致性状态。假如有三个sql语句…...

天线理论知识1——基础概念介绍
基础概念介绍 文章目录 基础概念介绍前言一、主要参数二、天线的种类三、天线的测量前言 天线是用于发射和接收电磁波设备。其功能可以概括为转换自由空间中的电磁波和设备中的导行波。 一、主要参数 天线设计中要考虑的参数较多,包括 方向性函数:距离天线 r r r处的远区…...

【云原生之Docker实战】使用Docker部署StackEdit在线Markdown编辑器
【云原生之Docker实战】使用Docker部署StackEdit在线Markdown编辑器 一、StackEdit介绍1.StackEdit简介2.StackEdit中文版简介3.StackEdit中文版功能二、检查本地Docker环境1.检查系统版本2.检查系统Docker版本3.检查docker compose版本三、下载StackEdit镜像四、部署StackEdit…...
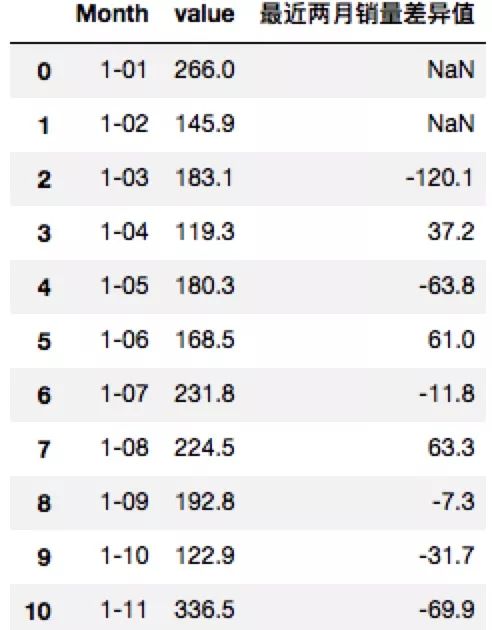
特征工程:特征构造以及时间序列特征构造
数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。由此可见,特征工程在机器学习中占有相当重要的地位。在实际应用当中,可以说特征工程是机器学习成功的关键。 那特征工程是什么? 特征工程是利用数据领域的相关…...

单master部署简要步骤
准备多台服务器,选定一台为master例如设置ip为192.168.0.10,host: k8s.master,其他分别为 k8s.s11 192.168.0.11k8s.s12 192.168.0.12....hostname可以使用命令配置hostname k8s.masterip解析可以在hosts文件中写入,如果有内部dns解析可以在内…...
基础算法 --- 前缀和与差分)
【算法基础】(一)基础算法 --- 前缀和与差分
✨个人主页:bit me ✨当前专栏:算法基础 🔥专栏简介:该专栏主要更新一些基础算法题,有参加蓝桥杯等算法题竞赛或者正在刷题的铁汁们可以关注一下,互相监督打卡学习 🌹 🌹 dz…...

c++提高篇——stack容器
一、stack容器的基本概念 stack是一种先进后出(FILO)的数据结构,它只有一个出口。栈中只有顶端的元素才可以被外界使用。因此该容器不能有遍历行为。基本的结构如下: stack容器有些像手枪子弹的弹夹,其数据的出入栈可以以弹夹为参考。 二、…...

HTTP安全与HTTPS协议
目录 Http协议的安全问题 常见的加密方式 防止窃听 单向散列函数 单向散列值的特点 加密与解密 对称加密与非对称加密 对称加密的密钥配送问题 密钥配送问题的解决 非对称加密 前言: 公钥与私钥 非对称加密过程 混合密码系统 前言: 混合…...

【c++】类和对象4—c++对象模型和this指针
文章目录成员变量和成员函数分开存储this指针的用途空指针访问成员函数const修饰成员函数成员变量和成员函数分开存储 在c中,类内的成员变量和成员函数分开存储 只有非静态成员变量才属于类的对象上 #include<iostream> using namespace std;class Person1…...
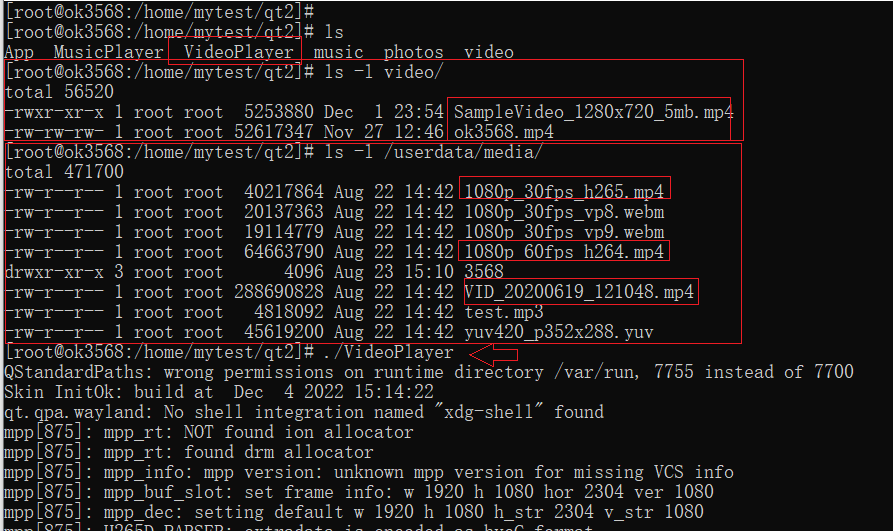
嵌入式Qt 开发一个视频播放器
上篇文章:嵌入式 Qt开发一个音乐播放器,使用Qt制作了一个音乐播放器,并在OK3568开发板上进行了运行测试,实际测试效果还不错。 本篇继续来实现一个Qt视频播放器软件,可以实现视频列表的显示与选择播放等,先…...

阿里巴巴内网 Spring Cloud Alibaba 强势来袭,开创微服务的新时代
Spring Cloud 发展史 Spring Cloud 从 15 年的 3 月份推出之后,迅速在 Java 微服务生态中,成为开发人员的首选技术栈。 Spring Cloud 在 Spring Boot 的基础上,保留 Java 开发习惯,加入分布式特性,提供了一系列通用工…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
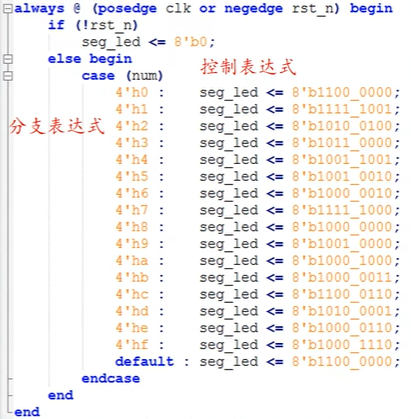
ZYNQ学习记录FPGA(二)Verilog语言
一、Verilog简介 1.1 HDL(Hardware Description language) 在解释HDL之前,先来了解一下数字系统设计的流程:逻辑设计 -> 电路实现 -> 系统验证。 逻辑设计又称前端,在这个过程中就需要用到HDL,正文…...