【算法基础】(一)基础算法 --- 前缀和与差分
✨个人主页:bit me
✨当前专栏:算法基础
🔥专栏简介:该专栏主要更新一些基础算法题,有参加蓝桥杯等算法题竞赛或者正在刷题的铁汁们可以关注一下,互相监督打卡学习 🌹 🌹 🌹
前 缀 和 与 差 分
- 🎄一. 前缀和(一维)
- 🌲二. 子矩阵的和(二维)
- 🌳三. 差分
- 🌴四. 差分矩阵
- 🎋五. 总结
🎄一. 前缀和(一维)
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中从第 l 个数到第 r 个数的和。
输入格式:
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
接下来 m 行,每行包含两个整数 l 和 r,表示一个询问的区间范围。
输出格式:
共 m 行,每行输出一个询问的结果。
数据范围:
1 ≤ l ≤ r ≤n,
1 ≤ n,m ≤ 100000,
−1000 ≤ 数列中元素的值 ≤ 1000
输入样例:
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例:
3
6
10
思路:
- 数组 a[1] + a[2] + … + a[i],对于某一个区间[l,r]的和就是s[r]-s[l-1]
- 考虑边界统一问题可以让 s[0] = 0 统一格式,但是我们题解可以让边界从角标 1 开始,有效避免让 s[0] = 0 来单独处理
题解:
- 把数都遍历到数组里
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int[] a = new int[n+1];
int[] s = new int[n+1];
for(int i = 1 ; i <= n ; i ++ ){a[i] = scan.nextInt();
}
- 前 n 项数组和
for(int i = 1 ; i <= n ; i ++){s[i] = s[i-1] + a[i];
}
- 根据规律某一个区间[l,r]的和就是s[r]-s[l-1]
while(m-- > 0){int l = scan.nextInt();int r = scan.nextInt();System.out.println(s[r] - s[l-1]);
}
附上总的代码
import java.util.Scanner;
public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();int[] a = new int[n+1];int[] s = new int[n+1];for(int i = 1 ; i <= n ; i ++ ){a[i] = scan.nextInt();}for(int i = 1 ; i <= n ; i ++){s[i] = s[i-1] + a[i];}while(m-- > 0){int l = scan.nextInt();int r = scan.nextInt();System.out.println(s[r] - s[l-1]);}
}
🌲二. 子矩阵的和(二维)
输入一个 n 行 m 列的整数矩阵,再输入 q 个询问,每个询问包含四个整数x1,y1,x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式:
第一行包含三个整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含四个整数 x1,y1,x2,y2,表示一组询问。
输出格式:
共 q 行,每行输出一个询问的结果。
数据范围:
1 ≤ n,m ≤1000,
1 ≤ q ≤ 200000,
1 ≤ x1 ≤ x2 ≤n,
1 ≤ y1 ≤ y2 ≤m,
−1000 ≤ 矩阵内元素的值 ≤ 1000
输入样例:
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例:
17
27
21
思路:
此处视图就不画了,我们要先了解清楚计算的公式
- s[i,j] = s[i - 1,j] + s[i,j - 1] - s[i - 1,j - 1] + a[i,j]
- (x1, y1),(x2, y2) 这一矩阵中所有数的和 = s[x2,y2] - s[x2,y1 - 1] - s[x1 - 1,y2] + s[x1 - 1,y1 - 1]
题解:
- 继续按照上题一样,角标都从 1 开始,因此数组都要扩容 + 1
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int q = scan.nextInt();
int[][] a = new int[n+1][m+1];
int[][] s = new int[n+1][m+1];
for(int i = 1 ; i <= n ; i ++ ){for(int j = 1 ;j <= m ; j ++ ){a[i][j] = scan.nextInt();}
}
- 按照思路计算二维数组每一块从 (1,1) 到 (i,j) 的大小,得出 s[i,j] 的通式
for(int i = 1 ; i <= n ; i ++ ){for(int j = 1 ;j <= m ; j ++ ){s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];}
}
- 通式计算区域相加减的出的面积
while(q-->0){int x1 = scan.nextInt();int y1 = scan.nextInt();int x2 = scan.nextInt();int y2 = scan.nextInt();System.out.println(s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]);
}
附上总的代码
import java.util.Scanner;
public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();int q = scan.nextInt();int[][] a = new int[n+1][m+1];int[][] s = new int[n+1][m+1];for(int i = 1 ; i <= n ; i ++ ){for(int j = 1 ;j <= m ; j ++ ){a[i][j] = scan.nextInt();}}for(int i = 1 ; i <= n ; i ++ ){for(int j = 1 ;j <= m ; j ++ ){s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];}}while(q-->0){int x1 = scan.nextInt();int y1 = scan.nextInt();int x2 = scan.nextInt();int y2 = scan.nextInt();System.out.println(s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]);}
}
🌳三. 差分
输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数 l,r,c,表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式:
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数序列。
接下来 m 行,每行包含三个整数 l,r,c,表示一个操作。
输出格式:
共一行,包含 n 个整数,表示最终序列。
数据范围:
1 ≤ n,m ≤ 100000,
1 ≤ l ≤ r ≤ n,
−1000 ≤ c ≤ 1000,
−1000 ≤ 整数序列中元素的值 ≤ 1000
输入样例:
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例:
3 4 5 3 4 2
思路:
- 差分是求前缀和的逆操作,如果想将a数组中 [l,r] 部分的数据全部加上c,只需要将 b[l] + c,然后 b[r+1] - c 即可。
差分操作和前缀和一样数组下标都从1开始。b[l] + c 后,l后面的数组都会加 c。r 后面的数据也会被改变,要改回来就得 b[r+1] - c- 求a[i]的值: 其实就是求b数组的一位前缀和
题解:
- 先解决范围问题
static int N = 1000010;
static int[] a = new int[N];
static int[] b = new int[N];
- 数据遍历进数组
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
for(int i = 1 ; i <= n ; i ++ ){a[i] = scan.nextInt();
}
- 构造一下b数组,因为a是b数组的前缀和
for(int i = 1 ; i <= n ; i ++ ){b[i] = a[i] - a[i - 1];
}
- 将a数组中 [l,r] 部分的数据全部加上c
while(m -- > 0){int l = scan.nextInt();int r = scan.nextInt();int c = scan.nextInt();b[l] += c;b[r + 1] -= c;
}
- 最后求一遍差分数组的前缀和
for(int i = 1 ; i <= n ; i ++ ){b[i] += b[i - 1];System.out.print(b[i] + " ");
}
附上总的代码
import java.util.*;public class Test {static int N = 1000010;static int[] a = new int[N];static int[] b = new int[N];public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();for(int i = 1 ; i <= n ; i ++ ){a[i] = scan.nextInt();}for(int i = 1 ; i <= n ; i ++ ){b[i] = a[i] - a[i - 1];}while(m -- > 0){int l = scan.nextInt();int r = scan.nextInt();int c = scan.nextInt();b[l] += c;b[r + 1] -= c;}for(int i = 1 ; i <= n ; i ++ ){b[i] += b[i - 1];System.out.print(b[i] + " ");}}
}
🌴四. 差分矩阵
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
输入格式:
第一行包含整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式:
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围:
1 ≤ n,m ≤ 1000,
1 ≤ q ≤ 100000,
1 ≤ x1 ≤ x2 ≤ n,
1 ≤ y1 ≤ y2 ≤ m,
−1000 ≤ c ≤ 1000,
−1000 ≤ 矩阵内元素的值 ≤ 1000
输入样例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例:
2 3 4 1
4 3 4 1
2 2 2 2
思路:
- 对差分数组操作: b[x1][y1] += c; b[x1 -1][y2] -= c;b[x2][y1 -1] -= c; b[x2 - 1][y2 - 1] += c;
- 求a的差分数组b:b[i][j] =a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];
题解:
- 创建原数组 同时也是b的前缀和数组,a的差分数组
canner sc = new Scanner (System.in);
int n = sc.nextInt() , m = sc.nextInt(), q = sc.nextInt();
int[][] a = new int[1010][1010];//原数组 同时也是b的前缀和数组
int[][] b = new int[1010][1010];//a的差分数组
for(int i = 1;i <= n; i ++) {for(int j = 1; j <= m; j ++) {a[i][j] = sc.nextInt();}
}
- 求a的差分数组b
for(int i = 1;i <= n; i ++) {for(int j = 1; j <= m; j ++) {b[i][j] =a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];}
}
- 对差分数组操作
for(int i = 0; i < q; i ++) {int x1 = sc.nextInt(),y1 = sc.nextInt(),x2 = sc.nextInt(),y2 = sc.nextInt() ,c = sc.nextInt();b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}
- 再对b数组求一遍前缀和数组 并输出
for(int i = 1;i <= n; i ++) {for(int j = 1; j <= m; j ++) {a[i][j] = b[i][j] + a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];System.out.print(a[i][j] + " ");}System.out.println();
}
附上总的代码
import java.util.*;
public class Main{
public static void main(String[] args) {Scanner sc = new Scanner (System.in);int n = sc.nextInt() , m = sc.nextInt(), q = sc.nextInt();int[][] a = new int[1010][1010];int[][] b = new int[1010][1010];for(int i = 1;i <= n; i ++) {for(int j = 1; j <= m; j ++) {a[i][j] = sc.nextInt();}}for(int i = 1;i <= n; i ++) {for(int j = 1; j <= m; j ++) {b[i][j] =a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];}}for(int i = 0; i < q; i ++) {int x1 = sc.nextInt(),y1 = sc.nextInt(),x2 = sc.nextInt(),y2 = sc.nextInt() ,c = sc.nextInt();b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;}for(int i = 1;i <= n; i ++) {for(int j = 1; j <= m; j ++) {a[i][j] = b[i][j] + a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];System.out.print(a[i][j] + " ");}System.out.println();}
}
}
🎋五. 总结
简单的对于一维、二维以及三维的前缀和和差分的计算公式做一个简单的整理:
这里要知道对于n维的前缀和或者差分有 2^n 项
- 前缀和
一维前缀和: s[i] = s[i-1] + a[i]
求[l, r]区间的和:s[r] - s[l-1]
二维前缀和:s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j]
求[x1, y1] 到 [x2, y2]的和: s[x2][y2] - s[x1-1][y2] + s[x2][y1-1] - s[x1-1][y1-1]
- 差分
一维差分: 将[l, r]上的所有数+c :b[l] += c , b[r+1] -= c
求a[i]的值: 其实就是求b数组的一位前缀和
二维差分: 将[x1, y1]到[x2, y2]上的数字+c: b[x1][x2]+=c , b[x2+1][y1] -= c , b[x1][y2+1] -=c , b[x2+1][y2+1] +=c
求a[i]的值: 其实就是求b数组的二维前缀和
相关文章:
基础算法 --- 前缀和与差分)
【算法基础】(一)基础算法 --- 前缀和与差分
✨个人主页:bit me ✨当前专栏:算法基础 🔥专栏简介:该专栏主要更新一些基础算法题,有参加蓝桥杯等算法题竞赛或者正在刷题的铁汁们可以关注一下,互相监督打卡学习 🌹 🌹 dz…...

c++提高篇——stack容器
一、stack容器的基本概念 stack是一种先进后出(FILO)的数据结构,它只有一个出口。栈中只有顶端的元素才可以被外界使用。因此该容器不能有遍历行为。基本的结构如下: stack容器有些像手枪子弹的弹夹,其数据的出入栈可以以弹夹为参考。 二、…...

HTTP安全与HTTPS协议
目录 Http协议的安全问题 常见的加密方式 防止窃听 单向散列函数 单向散列值的特点 加密与解密 对称加密与非对称加密 对称加密的密钥配送问题 密钥配送问题的解决 非对称加密 前言: 公钥与私钥 非对称加密过程 混合密码系统 前言: 混合…...

【c++】类和对象4—c++对象模型和this指针
文章目录成员变量和成员函数分开存储this指针的用途空指针访问成员函数const修饰成员函数成员变量和成员函数分开存储 在c中,类内的成员变量和成员函数分开存储 只有非静态成员变量才属于类的对象上 #include<iostream> using namespace std;class Person1…...
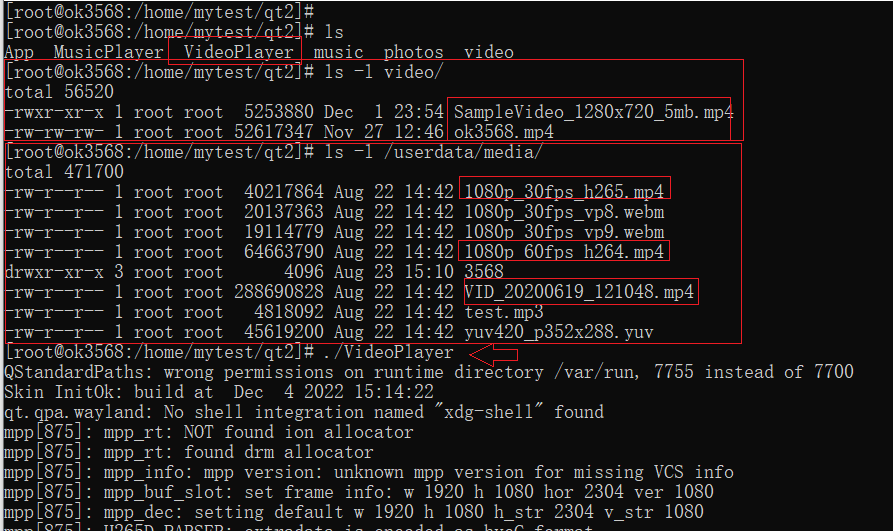
嵌入式Qt 开发一个视频播放器
上篇文章:嵌入式 Qt开发一个音乐播放器,使用Qt制作了一个音乐播放器,并在OK3568开发板上进行了运行测试,实际测试效果还不错。 本篇继续来实现一个Qt视频播放器软件,可以实现视频列表的显示与选择播放等,先…...

阿里巴巴内网 Spring Cloud Alibaba 强势来袭,开创微服务的新时代
Spring Cloud 发展史 Spring Cloud 从 15 年的 3 月份推出之后,迅速在 Java 微服务生态中,成为开发人员的首选技术栈。 Spring Cloud 在 Spring Boot 的基础上,保留 Java 开发习惯,加入分布式特性,提供了一系列通用工…...
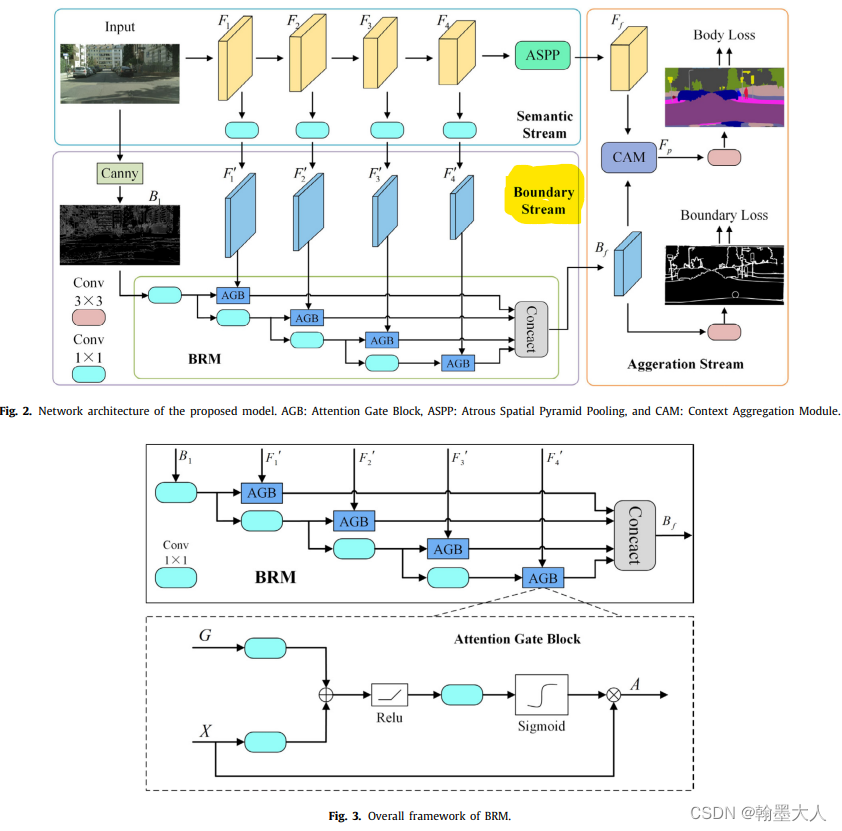
边界检测方法总结
1:经典的边界检测方法有sobel,拉普拉斯,canny等。 sobel: def get_sobel(in_chan, out_chan):filter_x np.array([[1, 0, -1],[2, 0, -2],[1, 0, -1],]).astype(np.float32)filter_y np.array([[1, 2, 1],[0, 0, 0],[-1, -2, -…...

Softing dataFEED OPC Suite Extended新版本支持从XML文件中读取生产数据
Softing dataFEED OPC Suite Extended V5.25的新功能——“文件读取(File Read)”,支持访问XML文件中可用的过程数据。 (文件读取功能支持获取由XML文件提供的过程数据)dataFEED OPC Suite Extended是用于OPC通信和云连…...
央行罚单!金融机构被罚原因揭秘
近日,人民银行公布了2023年首批行政处罚罚单,引发业内广泛关注。 顶象防御云业务安全情报中心统计了人民银行官网,2020年1月至2023年2月10日期间,公布的101份行政处罚。 统计显示,16家金融机构被罚27066.9万元&#…...

js中var、let、const详解
首先 var、let、const 在项目开发中都是用来声明变量的,在ES5中只有两种声明变量的方法:var和function,在ES6中新增了 let、const、class、import 四种声明变量的方法,本文主要讲解 var、let 与 const 的语法,其他的大…...
,真的很详细,一篇文章你就会了)
【数据库】MySQL概念知识语法-基础篇(DCL),真的很详细,一篇文章你就会了
目录通用语法及分类DCL(数据控制语言)管理用户查询用户权限控制函数字符串函数数值函数日期函数流程函数约束外键约束多表查询一对多多对多一对一通用语法及分类 ● DDL: 数据定义语言,用来定义数据库对象(数据库、表、字段&…...
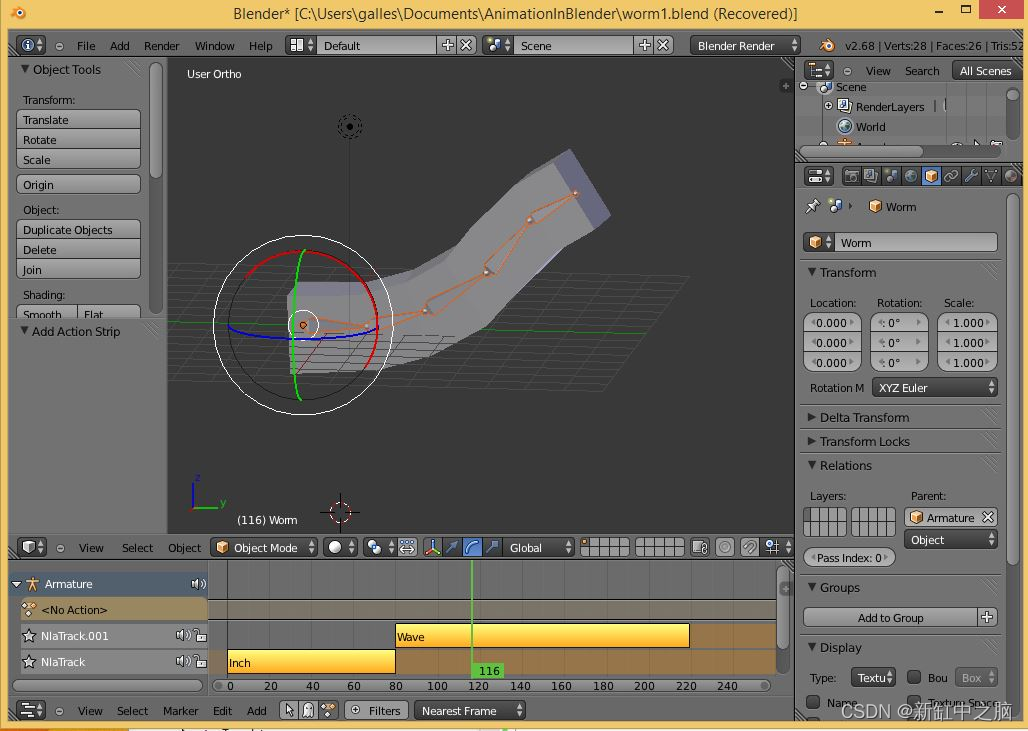
Blender骨骼动画快速教程
有关创建模型的更多详细信息,请参阅在 Blender 中创建模型。 我们将为这个例子做一个非常简单的模型——蠕虫! 从我们的初始立方体开始,进入编辑模式,切换到面选择,然后选择任何面: 推荐:将 NSD…...
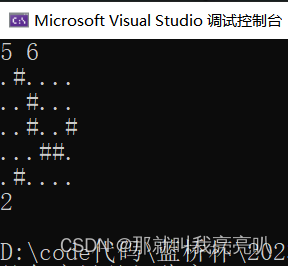
【C++算法】dfs深度优先搜索(下) ——【全面深度剖析+经典例题展示】
💃🏼 本人简介:男 👶🏼 年龄:18 🤞 作者:那就叫我亮亮叭 📕 专栏:关于C/C那点破事 文章目录0.0 写在前面1. 中国象棋1.1 题干信息① 背景说明概述② 问题描述…...
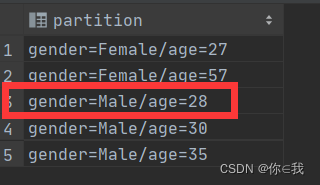
HIVE 基础(三)
目录 建表语句 表数据 Hive建表高阶语句 - CTAS and WITH CTAS – as select方式建表 CTE (CTAS with Common Table Expression) LIKE 创建临时表 清空表数据 修改表(Alter针对元数据) 改名 修正表文件格式 修改列名 添加列 替换列 动态分…...

redis-cluster集群搭建
安装redis所需环境 yum install -y gcc-c yum install -y wget 创建文件夹 cd / mkdir redis/redis-cluster/7001 cd redis/redis-cluster mkdir 7002 7003 7004 7005 7006 7007 7008下载redis压缩包并解压安装 wget https://download.redis.io/redis-stable.tar.gz tar -…...

【C语言】可变参数列表va_list
本篇博客让我们来认识一下C语言学习过程中往往被忽略的可变参数列表 所谓可变参数,就是一个不限定参数数量的函数,我们可以往里面传入任意个数的参数,以达成某些目的。 关联:C11可变模板参数 1.函数 #include <stdarg.h>…...
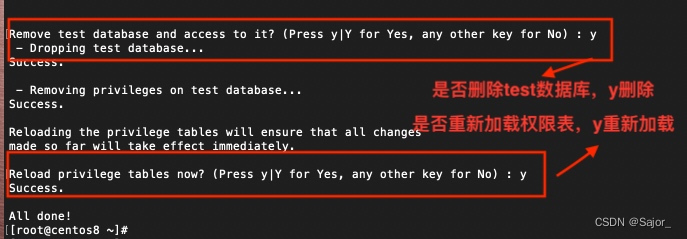
CentOS7.6 MySQL8安装
1 检查是否安装过 MySQL rpm -qa | grep -i mysqlmariadb rpm -qa | grep mariadb2 卸载之前的安装 MySQL rpm -e --nodeps 软件名 //强力删除,对相关依赖的文件也进行强力删除卸载 rpm -e --nodeps mariadb-libs-5.5.60-1.el7_5.x86_643 官网下载 MySQL :: D…...

安装Tomcat的步骤?
首先先完成JDK配置,javac -version 检测 1.把tomcat下载到本地硬盘 2.创建tomcat8.0文件夹,完成解压(免安装)4.打开解压之后的目录,进入bin目录,双击startup.bat,启动tomcat5.可以看到弹出一个黑色的窗口,不要关闭,如果关闭意味着…...

Redis之分布式锁
随着业务发展的需要,原单体单机部署的系统被演化成分布式集群系统后,由于分布式系统多线程、多进程并且分布在不同机器上,这将使原单机部署情况下的并发控制锁策略失效,单纯的 Java API并不能提供分布式锁的能力。为了解决这个问题…...

2022年中国前10电商GMV总结
我是卢松松,点点上面的头像,欢迎关注我哦! 1,阿里8万亿;2,京东3万亿;3,拼多多3万亿;4,小程序私域电商3万亿;5,抖音电商1.4万亿。6,抖音本地生活服务电商600亿。7…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
