2023高教社杯数学建模思路 - 复盘:光照强度计算的优化模型
文章目录
- 0 赛题思路
- 1 问题要求
- 2 假设约定
- 3 符号约定
- 4 建立模型
- 5 模型求解
- 6 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 问题要求
现在已知一个教室长为15米,宽为12米,在距离地面高2.5米的位置均
匀的安放4个光源(分别为1、2、3、4),各个光源的光照强度均为一个单位,如下图
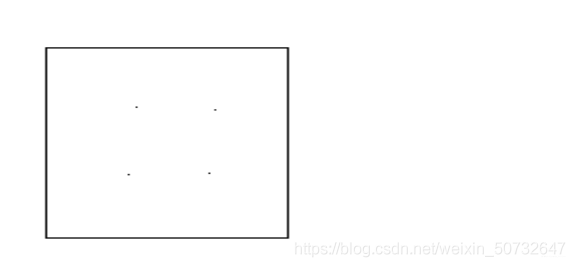
要求:
- (1)如何计算教室内任意一点的光照强度?(光源对目标点的光照强度与该光源到目标点距离的平方成反比,与该光源的强度成正比).
- (2)画出距离地面1米处各个点的光照强度与位置(横纵坐标)之间的函数关系曲面图,试同时给出一个近似的函数关系式.
- (3)假设离地面1米高正是学生桌面的高度,如何设计这四个点光源的位置,才能使学生对光照的平均满意度达到最高?
- (4)若将题目中的点光源换成线光源,以上(2)、(3)问的结果又如何?
(对于(1)、(2)问,假设横向(纵向)墙壁与光源、光源与光源、光源与墙壁之间的距离是相等的.)
2 假设约定
- 1 光不会通过窗、门等外涉,也不考虑光在空气中的消耗,即光照强度和不变;
- 2 室内不受外界光源影响;
- 3 教室高度为2.5米;
- 4 不考虑光的反射;
- 5 线光源发光是均匀的.
3 符号约定

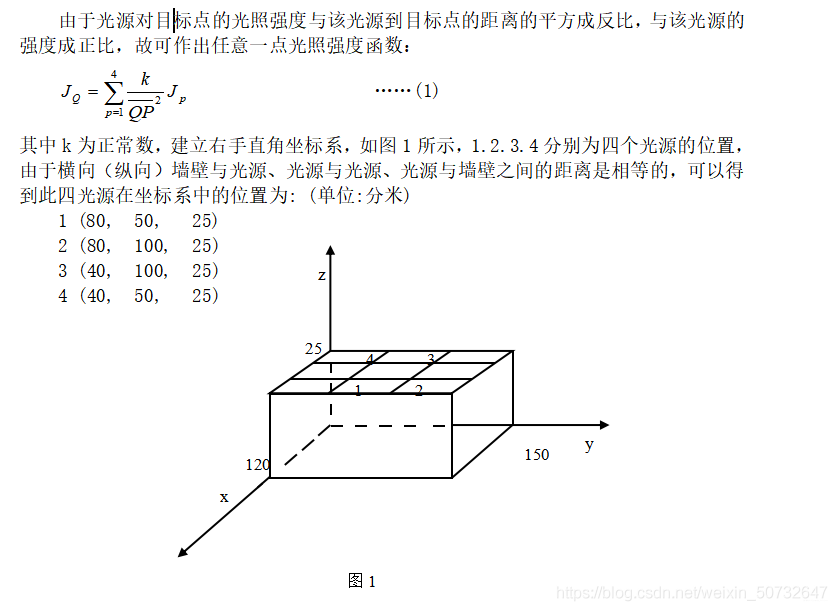
4 建立模型

5 模型求解

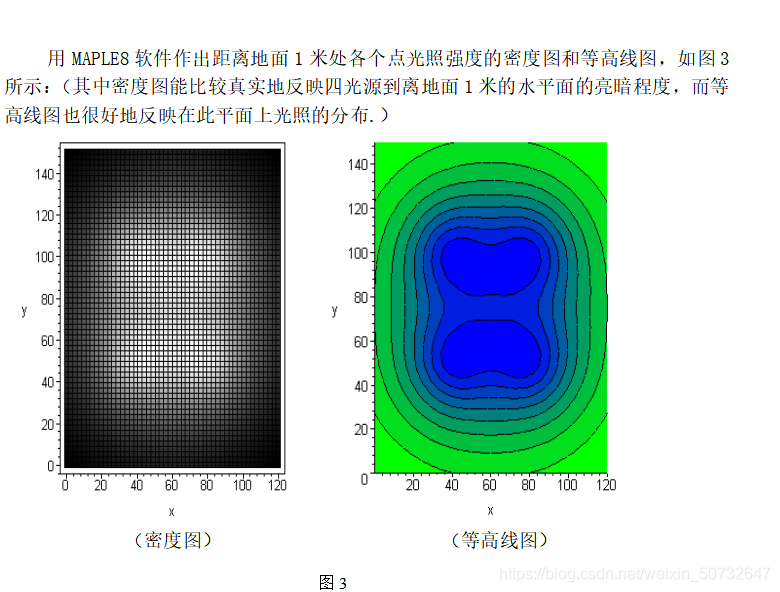
6 实现代码
matlab 实现代码
建议最好用python去实现,图会好看一些,而且国内当前趋势会逐渐淘汰matlab,目前有些学校已经无法使用matlab了
clear
clc
max=0;min=4;
for i=0:0.1:3for j=0.1:0.1:4s=0;x1=8+i,y1=5-jx2=8+i,y2=10+jx3=4-i,y3=10+jx4=4-i,y4=5-j for x=0:0.1:12for y=0:0.1:15for z=0:0.1:2.5if x1~=x & y1~=y & x2~=x & y2~=y & x3~=x & y3~=y & x4~=x & y4~=y s=s+1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2);endendendendk=4./s;l=0;z=1;for x=0:0.1:12for y=0:0.1:15l=l+k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));endendif l>maxmax=l;x11=x1;y11=y1;x12=x2;y12=y2;x13=x3;y13=y3;x14=x4;y14=y4;endp=l./(120.*150);Q=0;for x=0:0.1:12for y=0:0.1:15Q=Q+(k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2))-p).^2.^(1./2);endendif min>Qmin=Q;x21=x1;y21=y1;x22=x2;y22=y2;x23=x3;y23=y3;x24=x4;y24=y4;endend
end
disp(['最大值','x11=',num2str(x11),' ','y11=',num2str(y11),' ','x12=',num2str(x12),' ','y12=',num2str(y12),' ','x13=',num2str(x13),' ','y13=',num2str(y13),' ','x14=',num2str(x14),' ','y14=',num2str(y14)])
disp(['最平均','x21=',num2str(x21),' ','y21=',num2str(y21),' ','x22=',num2str(x22),' ','y22=',num2str(y22),' ','x23=',num2str(x23),' ','y23=',num2str(y23),' ','x24=',num2str(x24),' ','y24=',num2str(y24)])
附录二:
clear
clc
max=0;min=4;li=4;
for i=0:0.1:3for j=0.1:0.1:4s=0;x1=8+i,y1=5-jx2=8+i,y2=10+jx3=4-i,y3=10+jx4=4-i,y4=5-j for x=0:0.1:12for y=0:0.1:15for z=0:0.1:2.5if x1~=x & y1~=y & x2~=x & y2~=y & x3~=x & y3~=y & x4~=x & y4~=y s=s+1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2);endendendendk=4./s;l=0;z=1;e=0for x=0:0.1:12for y=0:0.1:15l=l+k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));r=k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));e=e+(r-6*10^(-32))^2;endendS=(l-0.1278)^2+eif S<lili=Sx11=x1,y11=y1, x12=x2,y12=y2, x13=x3,y13=y3, x14=x4,y14=y4,en4en4
en4
disp(['x11=',num2str(x11),' ','y11=',num2str(y11),' ','x12=',num2str(x12),' ','y12=',num2str(y12),' ','x13=',num2str(x13),' ','y13=',num2str(y13),' ','x14=',num2str(x14),' ','y14=',num2str(y14)])
li
建模资料
资料分享: 最强建模资料


相关文章:

2023高教社杯数学建模思路 - 复盘:光照强度计算的优化模型
文章目录 0 赛题思路1 问题要求2 假设约定3 符号约定4 建立模型5 模型求解6 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 问题要求 现在已知一个教室长为15米,宽为12米&…...

河道漂浮物检测:安防监控/视频智能分析/AI算法智能分析技术如何助力河道整治工作?
随着社会的发展和人们生活水平的进步,水污染问题也越来越严重,水资源监管和治理成为城市发展的一大困扰,水面上的漂浮垃圾不仅会影响河道生态安全并阻碍船舶航行,还会影响人们的身体健康。 TSINGSEEE青犀AI智能分析平台在环保场景…...
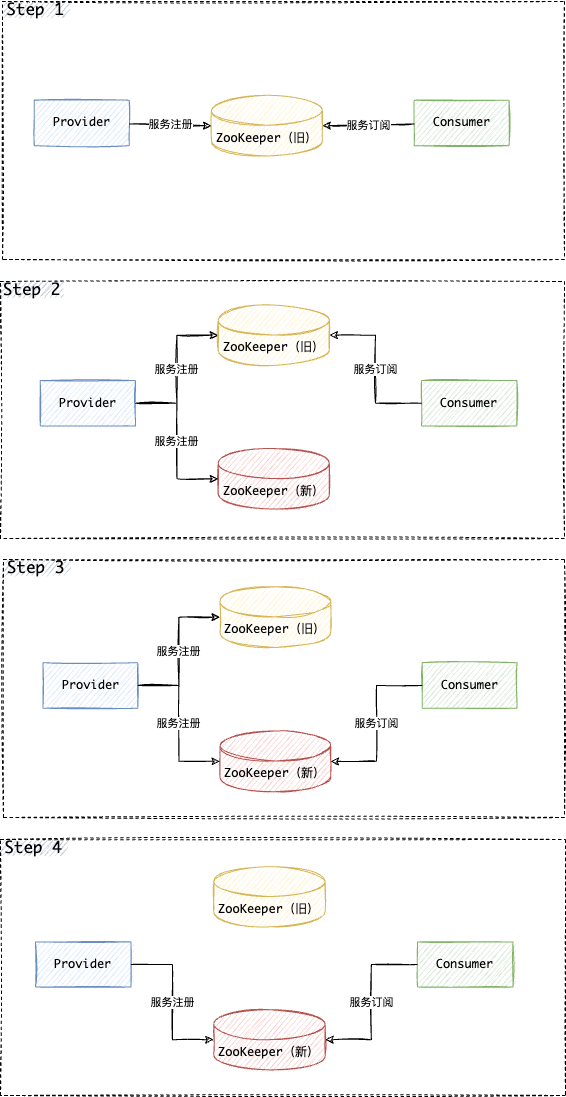
Dubbo 应用切换 ZooKeeper 注册中心实例,流量无损迁移
首先思考一个问题:如果 Dubbo 应用使用 ZooKeeper 作为注册中心,现在需要切换到新的 ZooKeeper 实例,如何做到流量无损? 本文提供解决这个问题的一种方案。 场景 有两个基于 Dubbo 的微服务应用,一个是服务提供者&…...

ADB入门教程
安卓开发 文章目录 安卓开发前言USB 连接链接 前言 基本用法 命令语法 adb 命令的基本语法如下: adb [-d|-e|-s <serialNumber>] <command>如果只有一个设备/模拟器连接时,可以省略掉 [-d|-e|-s ] 这一部分,直接使用 adb 。 为…...
SQLPro Studio for Mac:强大的SQL开发和管理工具
SQLPro Studio for Mac是一款强大的Mac上使用的SQL开发和管理工具,它支持各种数据库,包括MySQL,PostgreSQL,SQLite等。使用 SQLPro Studio,您可以轻松地连接和管理您的数据库,执行SQL查询和脚本,…...
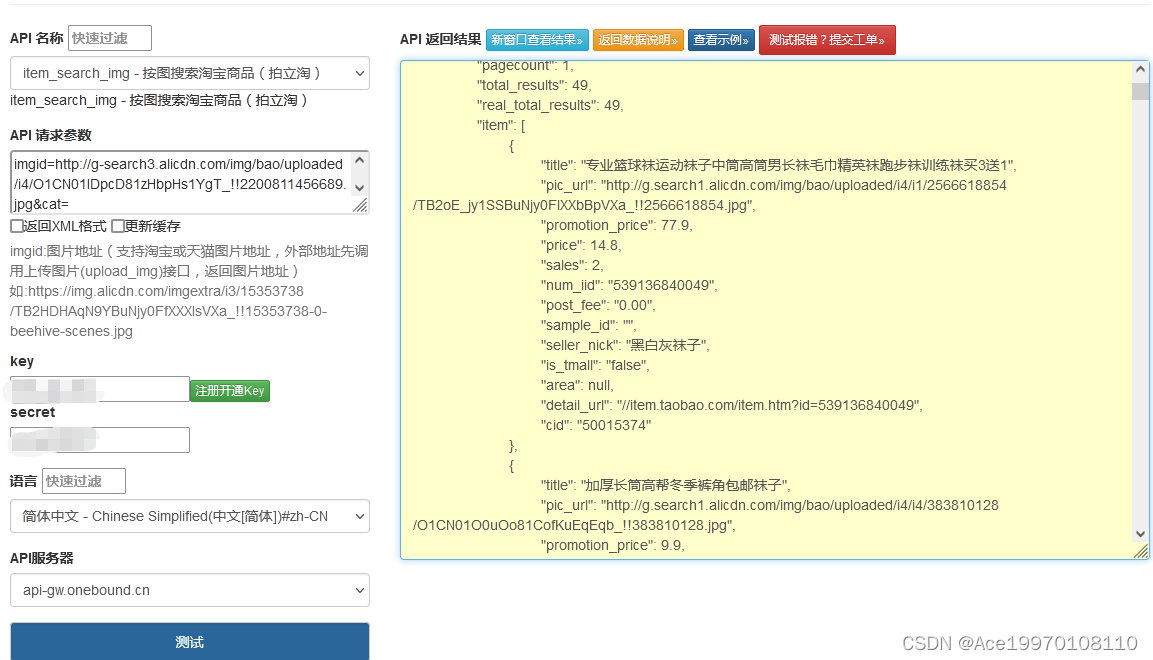
淘宝API技术解析,实现按图搜索淘宝商品
淘宝提供了开放平台接口(API)来实现按图搜索淘宝商品的功能。您可以通过以下步骤来实现: 1. 获取开放平台的访问权限:首先,您需要在淘宝开放平台创建一个应用,获取访问淘宝API的权限。具体的申请步骤和要求…...

错误:依赖检测失败: mysql-community-libs(x86-64) >= 5.7.9 被 (已安裝) mysql-community-li
错误: 错误原因:没有删除之前安装的依赖问题 解决办法: yum remove mysql-libs 再用下面指令检查一遍: rpm -qa | grep mysql 如果有还未清理的,用下面指令: rpm -e xxx...
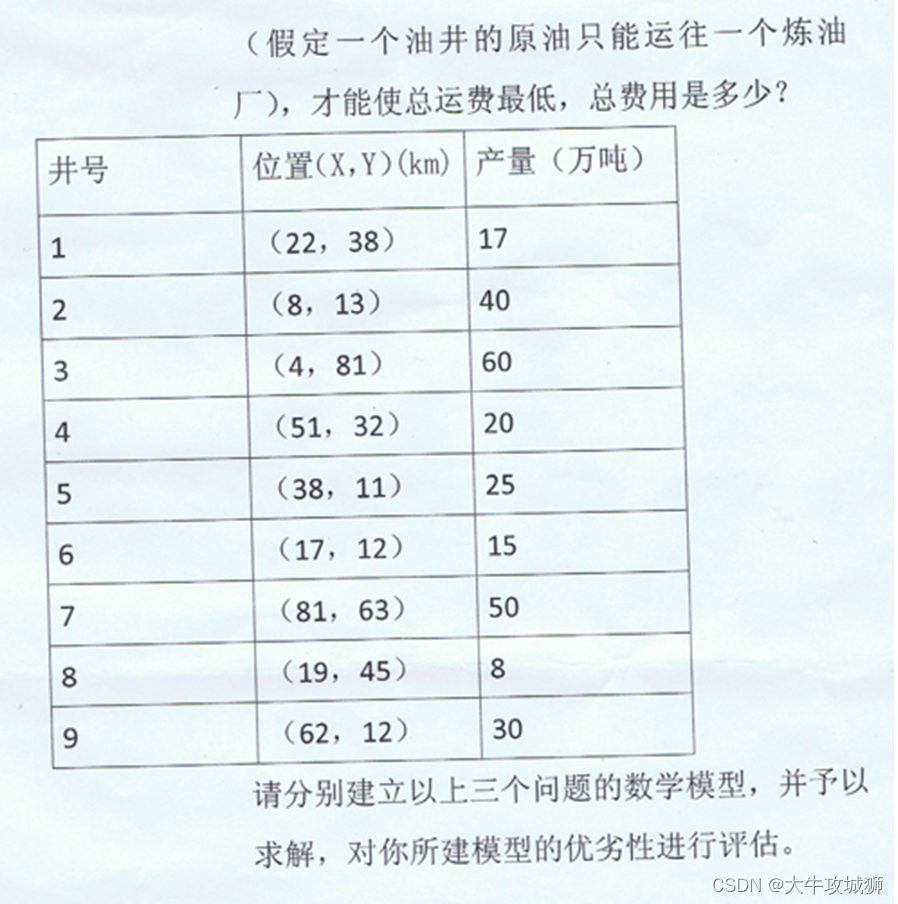
使用MATLAB解算炼油厂的选址
背景 记得有一年的数据建模大赛,试题是炼油厂的选址,最后我们采用MATLAB编写(复制)蒙特卡洛算法,还到了省级一等奖,这里把仅有一些记忆和材料,放到这里来,用来纪念消失的青春。 本…...

AudioTrack播放音乐之getMinBufferSize
1. AudioTrack播放音乐之前需要做好准备,即需要先计算最小音频数据缓存空间 文件路径:AudioTrack.java (frameworks\base\media\java\android\media) static public int getMinBufferSize(int sampleRateInHz, int channelConfig, int audioFormat) {@参数sampleRateInHz,…...

React和Redux中的不变性
https://overreacted.io/zh-hans/a-complete-guide-to-useeffect/ 一、不变性和副作用 1.不变:不断创造新值来替换旧值 2.不变性规则: (1)当给定相同的输入时,纯函数必须始终返回相同的值 (2࿰…...
NPM 常用命令(一)
目录 1、npm 1.1 简介 1.2 依赖性 1.3 安装方式 2、npm access 2.1 命令描述 2.2 详情 3、npm adduser 3.1 描述 4、npm audit 4.1 简介 4.2 审计签名 4.3 操作示例 4.4 配置 audit-level dry-run force json package-lock-only omit foreground-scripts …...

【ES6】Promise推荐用法
一般来说,不要在then()方法里面定义 Reject 状态的回调函数(即then的第二个参数),总是使用catch方法。 // bad promise.then(function(data) {// success}, function(err) {// error});// good promise.then(function(data) { //…...

【JavaScript】版本判断
用于客户端和服务端进行版本更新判断使用,如有BUG,还望指出 效果 console.log(isAllowUpdate(1,2.0.0), // trueisAllowUpdate(2.0,2.0.0), // falseisAllowUpdate(2.0,2.0.1), // trueisAllowUpdate(2.1.1,2.1.2), // trueisAllowUpdate(2.1.3,2.1.2),…...
Nano编辑器安装使用指南
关于nano Nano编辑器是一个命令行文本编辑器,具有简单易用的界面和一些基本功能。 Nano小巧友好,提供许多额外的特性,例如交互式的查找和替换、定位到指定的行列、自动缩进、特性切换、国际化支持、文件名标记完成等。 Nano是为了代替闭源的…...
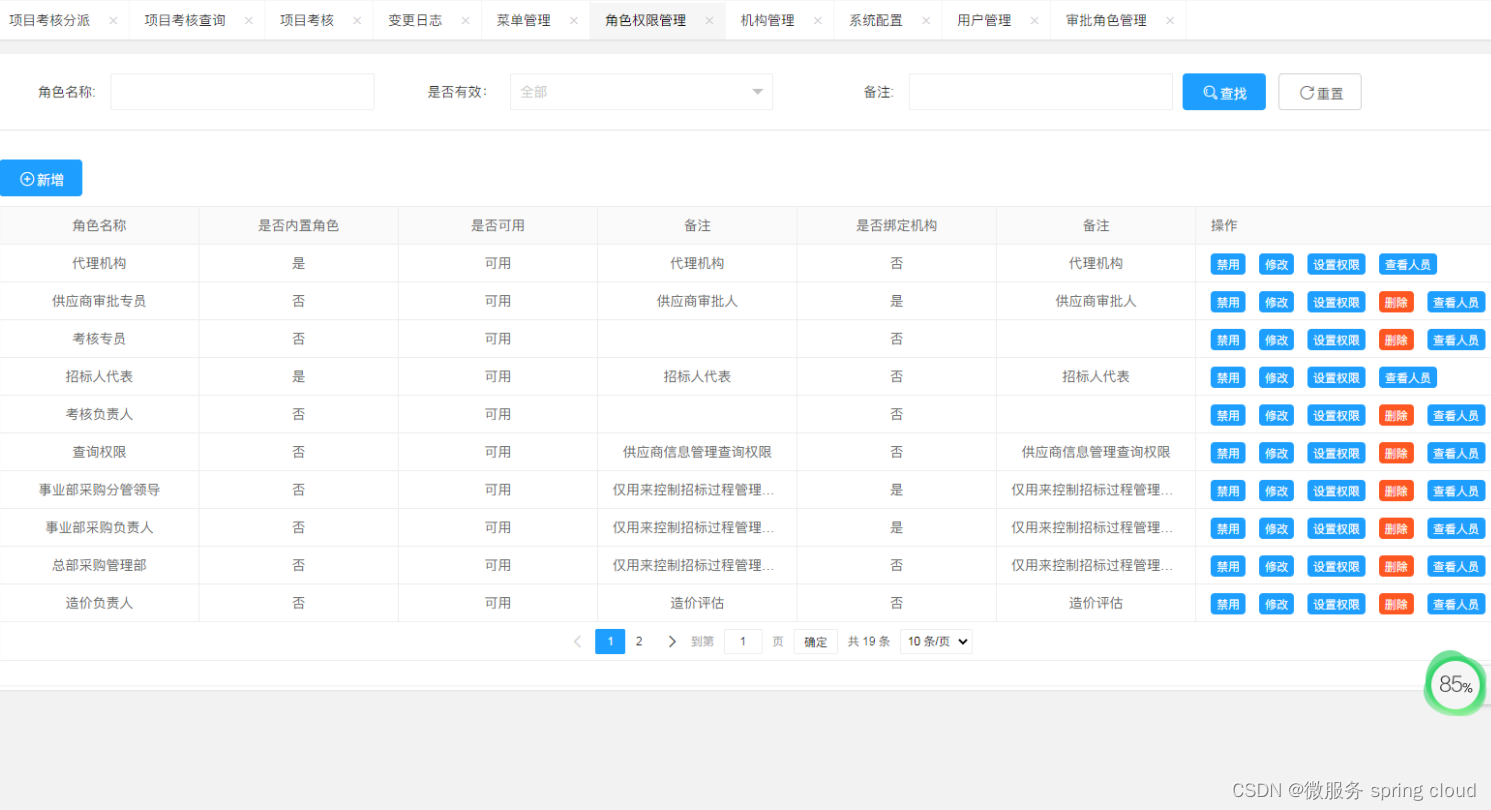
Java版电子招投标管理系统源码-电子招投标认证服务平台-权威认证
项目说明 随着公司的快速发展,企业人员和经营规模不断壮大,公司对内部招采管理的提升提出了更高的要求。在企业里建立一个公平、公开、公正的采购环境,最大限度控制采购成本至关重要。符合国家电子招投标法律法规及相关规范,以及…...
Java String类(1)
String类的重要性 我们之前在C语言中已经涉及到字符串了,但是在C语言中要表示字符串只能使用字符数组或者字符指针,可以使用标准库提供的字符串系列函数完成大部分操作,但是这种将数据和操作数据的方法分离开的方式不符合面向对象的思想&…...
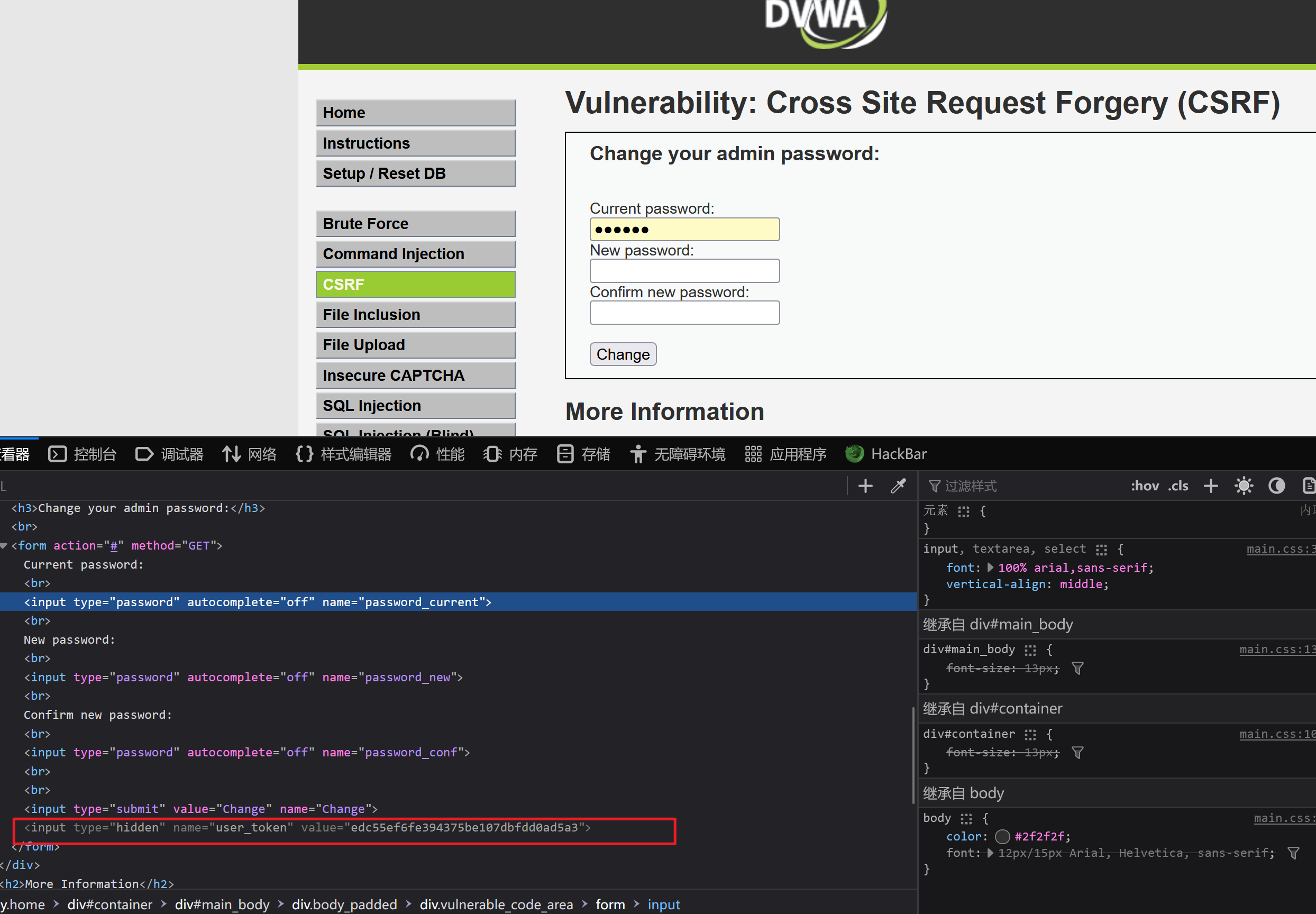
渗透测试漏洞原理之---【CSRF跨站请求伪造】
文章目录 1、CSRF概述1.1、基本原理1.1.1、基本概念1.1.2、关键点1.1.3、目标 1.2、CSRF场景1.2.1、银行支付转账1.2.2构造虚假网站1.2.3、场景建模 1.3、CSRF类别1.3.1、POST方式 1.4、CSRF验证1.4.1、CSRF PoC Generator 2、CSRF攻防2.1、CSRF实战2.1.1、与XSS 漏洞相结合 2.…...
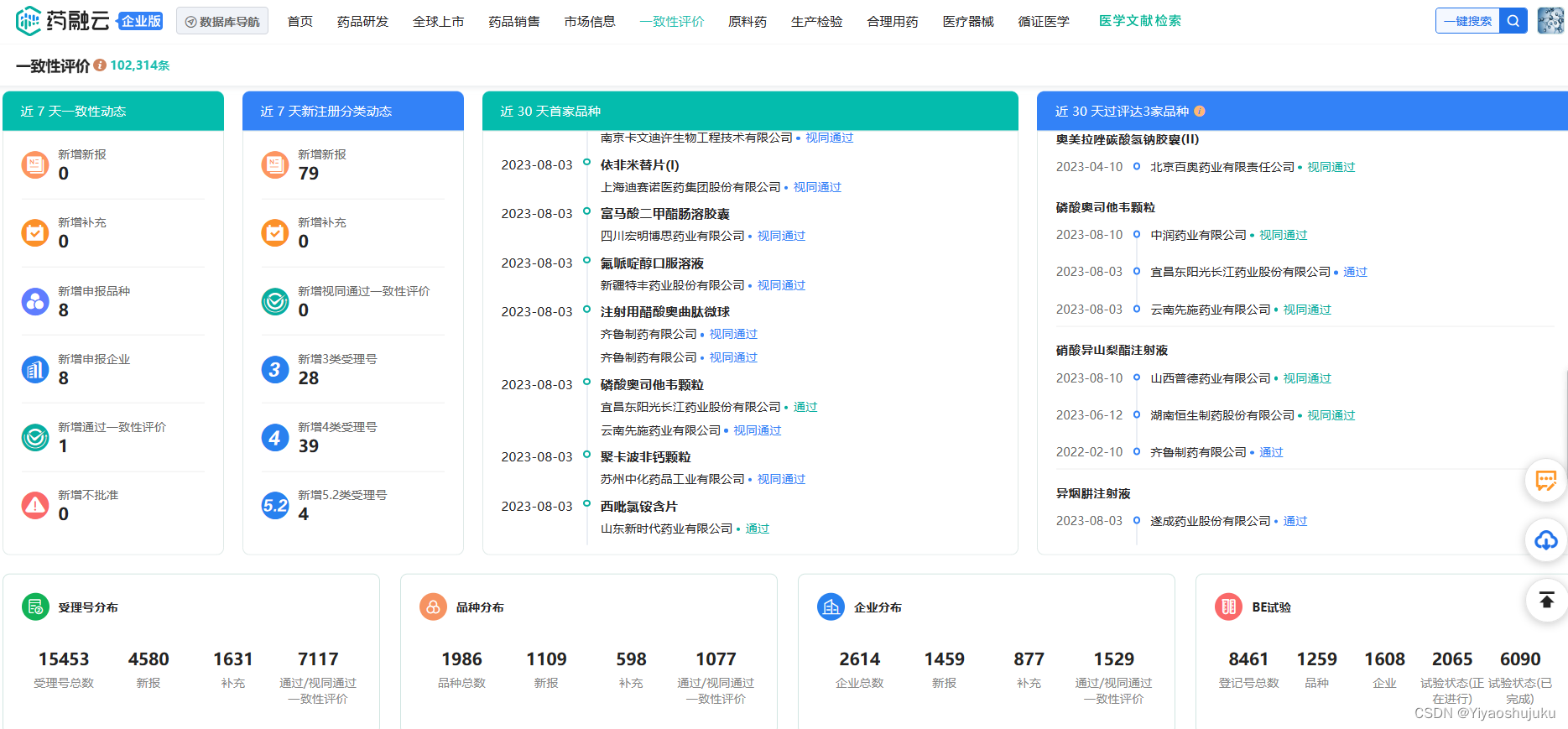
带量采购药品数据查询集采分析平台(建议收藏!)
药品集采常态化下对不同中标企业的影响不尽相同,对于市场份额较大且拥有多款重要药品的大型企业来说,集采能够保持其市场份额,尽管被集采的药品可能会面临销售下降的局面,但该企业还有其他产品可以填补,整体影响不大。…...

概念解析 | 无线感知的新篇章:异构网络感知的原理与挑战
注1:本文系“概念解析”系列之一,致力于简洁清晰地解释、辨析复杂而专业的概念。本次辨析的概念是:异构网络感知。 无线感知的新篇章:异构网络感知的原理与挑战 Interference Management in HetNets 在当今的无线通信领域,我们面临着一个重大的挑战:如何在有限的频谱资源…...
【大数据模型】让chatgpt为开发增速(开发专用提示词)
汝之观览,吾之幸也!本文主要聊聊怎样才能更好的使用提示词,给开发提速,大大缩减我们的开发时间,比如在开发中使用生成表结构脚本的提示词,生成代码的提示词等等。 一、准备 本文主要根据Claude进行演示&am…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
