使用MATLAB解算炼油厂的选址
背景
记得有一年的数据建模大赛,试题是炼油厂的选址,最后我们采用MATLAB编写(复制)蒙特卡洛算法,还到了省级一等奖,这里把仅有一些记忆和材料,放到这里来,用来纪念消失的青春。
本文使用素材下载,内含MATLAB代码
使用蒙特卡洛算法解算炼油厂的选址MATLAB程序,提供试题照片,以及MATLAB代码资源-CSDN文库
试题参考
如下图所示:

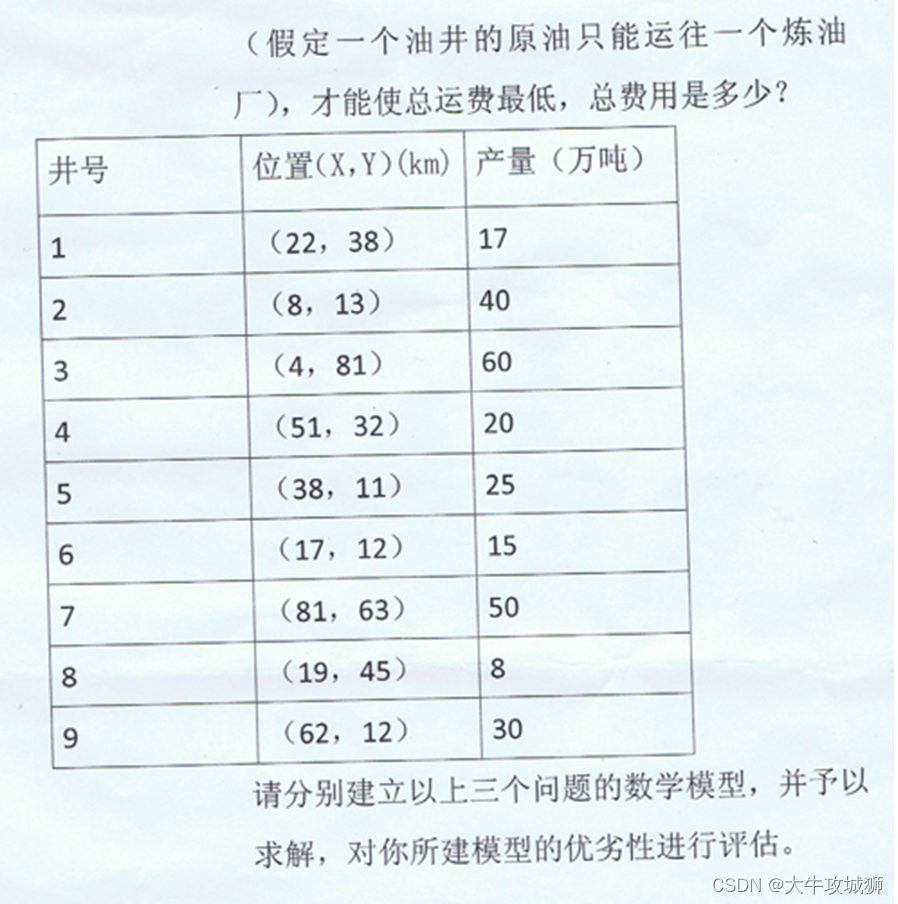
问题分析
问题一:
本问的炼油厂选址是九口油井的任一处,我们可以把九口油井依次作为炼油厂,然后分别计算其费用。
问题二:
本问的炼油厂选址范围应在0<横坐标x<100、0<纵坐标y<100,的矩形区域内。可以把问题转化为:在该矩形区域内找一点使其满足总费用最少。
问题三:
本问的两个炼油厂的选址纵横坐标都应在[0,82]的范围内。问即可转化成在该矩形区域内找两点,使其总费用最低。
模型假设
- 总费用与距离成正比,设比例系数为1;
- 总费用与油量成正比,设比例系数为1;
- 其他因素不影响总费用;
- 一口油井的原油智能运往一个炼油厂;
模型建立与求解
第一问模型:
设选1号油井为炼油厂产生的费用为feiyoug1;
选1号油井为炼油厂产生的费用为feiyoug1;
选2号油井为炼油厂产生的费用为feiyoug2;
选3号油井为炼油厂产生的费用为feiyoug3;
选4号油井为炼油厂产生的费用为feiyoug4;
…
…
选9号油井为炼油厂产生的费用为feiyoug9;
由问题一分析可知问题可转化为求
feiyong1=(abs(x2-x1)+abs(y2-y1))*chanliang2+(abs(x3-x1)+abs(y3-y1))*chanliang3+(abs(x4-x1)+abs(y4-y1))*chanliang4+(abs(x5-x1)+abs(y5-y1))*chanliang5+(abs(x6-x1)+abs(y6-y1))*chanliang6+(abs(x7-x1)+abs(y7-y1))*chanliang7+(abs(x8-x1)+abs(y8-y1))*chanliang8+(abs(x9-x1)+abs(y9-y1))*chanliang9
(其中abs是求绝对值,其余八个油井到1号油井的折线距离与产量之积作为费用,总费用即为八个油井产生费用之和)
同法可求feiyong2、feiyong3、……、feiyong9。
第一问求解:
利用matlab编程求解如下:
第一问程序:
x1=22;
y1=38;
x2=8;
y2=13;
x3=4;
y3=81;
x4=51;
y4=32;
x5=38;
y5=11;
x6=17;
y6=12;
x7=81;
y7=63;
x8=19;
y8=45;
x9=62;
y9=12;
chanliang1=17;
chanliang2=40;
chanliang3=60;
chanliang4=20;
chanliang5=25;
chanliang6=15;
chanliang7=50;
chanliang8=8;
chanliang9=30;
feiyong1=(abs(x2-x1)+abs(y2-y1))*chanliang2+(abs(x3-x1)+abs(y3-y1))*chanliang3+(abs(x4-x1)+abs(y4-y1))*chanliang4+(abs(x5-x1)+abs(y5-y1))*chanliang5+(abs(x6-x1)+abs(y6-y1))*chanliang6+(abs(x7-x1)+abs(y7-y1))*chanliang7+(abs(x8-x1)+abs(y8-y1))*chanliang8+(abs(x9-x1)+abs(y9-y1))*chanliang9
feiyong2=(abs(x1-x2)+abs(y1-y2))*chanliang1+(abs(x3-x2)+abs(y3-y2))*chanliang3+(abs(x4-x2)+abs(y4-y2))*chanliang4+(abs(x5-x2)+abs(y5-y2))*chanliang5+(abs(x6-x2)+abs(y6-y2))*chanliang6+(abs(x7-x2)+abs(y7-y2))*chanliang7+(abs(x8-x2)+abs(y8-y2))*chanliang8+(abs(x9-x2)+abs(y9-y2))*chanliang9
feiyong3=(abs(x1-x3)+abs(y1-y3))*chanliang1+(abs(x2-x3)+abs(y2-y3))*chanliang2+(abs(x4-x3)+abs(y4-y3))*chanliang4+(abs(x5-x3)+abs(y5-y3))*chanliang5+(abs(x6-x3)+abs(y6-y3))*chanliang6+(abs(x7-x3)+abs(y7-y3))*chanliang7+(abs(x8-x3)+abs(y8-y3))*chanliang8+(abs(x9-x3)+abs(y9-y3))*chanliang9
feiyong4=(abs(x1-x4)+abs(y1-y4))*chanliang1+(abs(x2-x4)+abs(y2-y4))*chanliang2+(abs(x3-x4)+abs(y3-y4))*chanliang3+(abs(x5-x4)+abs(y5-y4))*chanliang5+(abs(x6-x4)+abs(y6-y4))*chanliang6+(abs(x7-x4)+abs(y7-y4))*chanliang7+(abs(x8-x4)+abs(y8-y4))*chanliang8+(abs(x9-x4)+abs(y9-y4))*chanliang9
feiyong5=(abs(x1-x5)+abs(y1-y5))*chanliang1+(abs(x2-x5)+abs(y2-y5))*chanliang2+(abs(x3-x5)+abs(y3-y5))*chanliang3+(abs(x4-x5)+abs(y4-y5))*chanliang4+(abs(x6-x5)+abs(y6-y5))*chanliang6+(abs(x7-x5)+abs(y7-y5))*chanliang7+(abs(x8-x5)+abs(y8-y5))*chanliang8+(abs(x9-x5)+abs(y9-y5))*chanliang9
feiyong6=(abs(x1-x6)+abs(y1-y6))*chanliang1+(abs(x2-x6)+abs(y2-y6))*chanliang2+(abs(x3-x6)+abs(y3-y6))*chanliang3+(abs(x4-x6)+abs(y4-y6))*chanliang4+(abs(x5-x6)+abs(y5-y6))*chanliang5+(abs(x7-x6)+abs(y7-y6))*chanliang7+(abs(x8-x6)+abs(y8-y6))*chanliang8+(abs(x9-x6)+abs(y9-y6))*chanliang9
feiyong7=(abs(x1-x7)+abs(y1-y7))*chanliang1+(abs(x2-x7)+abs(y2-y7))*chanliang2+(abs(x3-x7)+abs(y3-y7))*chanliang3+(abs(x4-x7)+abs(y4-y7))*chanliang4+(abs(x5-x7)+abs(y5-y7))*chanliang5+(abs(x6-x7)+abs(y6-y7))*chanliang6+(abs(x8-x7)+abs(y8-y7))*chanliang8+(abs(x9-x7)+abs(y9-y7))*chanliang9
feiyong8=(abs(x1-x8)+abs(y1-y8))*chanliang1+(abs(x2-x8)+abs(y2-y8))*chanliang2+(abs(x3-x8)+abs(y3-y8))*chanliang3+(abs(x4-x8)+abs(y4-y8))*chanliang4+(abs(x5-x8)+abs(y5-y8))*chanliang5+(abs(x6-x8)+abs(y6-y8))*chanliang6+(abs(x7-x8)+abs(y7-y8))*chanliang7+(abs(x9-x8)+abs(y9-y8))*chanliang9
feiyong9=(abs(x1-x9)+abs(y1-y9))*chanliang1+(abs(x2-x9)+abs(y2-y9))*chanliang2+(abs(x3-x9)+abs(y3-y9))*chanliang3+(abs(x4-x9)+abs(y4-y9))*chanliang4+(abs(x5-x9)+abs(y5-y9))*chanliang5+(abs(x6-x9)+abs(y6-y9))*chanliang6+(abs(x7-x9)+abs(y7-y9))*chanliang7+(abs(x8-x9)+abs(y8-y9))*chanliang8
第一问运行结果:
feiyong1 =
13720
feiyong2 =
15317
feiyong3 =
18635
feiyong4 =
14835
feiyong5 =
15185
feiyong6 =
14857
feiyong7 =
20108
feiyong8 =
13980
feiyong9 =
16970
由程序运行结果可知:
feiyong1最小,即炼油厂建在1号油井附近,总费用最少。
第二问模型:
由分析可设该炼油厂得地址为(x(1),x(2)),且0<x(1)<100,0<x(2)<100
即求zongfeiyong最小
zongfeiyong=17*sqrt((x(1)-22)^2+(x(2)-38)^2)+40*sqrt((x(1)-8)^2+(x(2)-13)^2)+60*sqrt((x(1)-4)^2+(x(2)-81)^2)+20*sqrt((x(1)-51)^2+(x(2)-32)^2)+25*sqrt((x(1)-38)^2+(x(2)-11)^2)+15*sqrt((x(1)-17)^2+(x(2)-12)^2)+50*sqrt((x(1)-81)^2+(x(2)-63)^2)+8*sqrt((x(1)-19)^2+(x(2)-45)^2)+30*sqrt((x(1)-62)^2+(x(2)-12)^2);
其中sqrt为平方的意思,分别求的每个油井的到炼油厂的距离与其产量的积,再作和,即为总费用。
第二问用matlab编程求解如下(利用matlab总求最优解函数fmincon):
第二问程序:
function zongfeiyong=timu2(x)
zongfeiyong=17*sqrt((x(1)-22)^2+(x(2)-38)^2)+40*sqrt((x(1)-8)^2+(x(2)-13)^2)+60*sqrt((x(1)-4)^2+(x(2)-81)^2)+20*sqrt((x(1)-51)^2+(x(2)-32)^2)+25*sqrt((x(1)-38)^2+(x(2)-11)^2)+15*sqrt((x(1)-17)^2+(x(2)-12)^2)+50*sqrt((x(1)-81)^2+(x(2)-63)^2)+8*sqrt((x(1)-19)^2+(x(2)-45)^2)+30*sqrt((x(1)-62)^2+(x(2)-12)^2);
xmin=[0;0];
xmax=[100;100];
[x,fopt,flag,c]=fmincon('timu2',zeros(2,1),[],[],[],[],xmin,xmax)
第二问运行结果:
x =
32.4224
35.0597
fopt =
1.0213e+004
flag =
5
c =
iterations: 8
funcCount: 26
lssteplength: 1
stepsize: 2.0001e-004
algorithm: [1x44 char]
firstorderopt: 5.9487e-004
constrviolation: -32.4224
message: [1x844 char]
由程序运行结果可知:
即选址坐标为(32.4224,35.0597)
此时总费用最少为10213
第三问模型:
我们可以在纵、横坐标都为[0,82]的范围内任意选取两点做炼油厂。总费用即可转换为RES=min(17*sqrt((x(1)-22)^2+(x(2)-38)^2),17*sqrt((x(3)-22)^2+(x(4)-38)^2))+min(40*sqrt((x(1)-8)^2+(x(2)-13)^2),40*sqrt((x(3)-8)^2+(x(4)-13)^2))+min(60*sqrt((x(1)-4)^2+(x(2)-81)^2),60*sqrt((x(3)-4)^2+(x(4)-81)^2))+min(20*sqrt((x(1)-51)^2+(x(2)-32)^2),20*sqrt((x(3)-51)^2+(x(4)-32)^2))+min(25*sqrt((x(1)-38)^2+(x(2)-11)^2),25*sqrt((x(3)-38)^2+(x(4)-11)^2))+min(15*sqrt((x(1)-17)^2+(x(2)-12)^2),15*sqrt((x(3)-17)^2+(x(4)-12)^2))+min(50*sqrt((x(1)-81)^2+(x(2)-63)^2),50*sqrt((x(3)-81)^2+(x(4)-63)^2))+min(8*sqrt((x(1)-19)^2+(x(2)-45)^2),8*sqrt((x(3)-19)^2+(x(4)-45)^2))+min(30*sqrt((x(1)-62)^2+(x(2)-12)^2),30*sqrt((x(3)-62)^2+(x(4)-12)^2))
其中min(A,B)是求A、B中较小的数。
第三问求解:
利用蒙特卡洛算法,我们对x(1),x(2),x(3), x(4)随机生成一千万组(范围在[0,82]内),带入总费用公式RES中。求得其中最小值。利用matlab编程如下(程序多次运行):
第三问程序:
% 原函数
function RES=myobjfunc(x)
RES=min(17*sqrt((x(1)-22)^2+(x(2)-38)^2),17*sqrt((x(3)-22)^2+(x(4)-38)^2))+min(40*sqrt((x(1)-8)^2+(x(2)-13)^2),40*sqrt((x(3)-8)^2+(x(4)-13)^2))+min(60*sqrt((x(1)-4)^2+(x(2)-81)^2),60*sqrt((x(3)-4)^2+(x(4)-81)^2))+min(20*sqrt((x(1)-51)^2+(x(2)-32)^2),20*sqrt((x(3)-51)^2+(x(4)-32)^2))+min(25*sqrt((x(1)-38)^2+(x(2)-11)^2),25*sqrt((x(3)-38)^2+(x(4)-11)^2))+min(15*sqrt((x(1)-17)^2+(x(2)-12)^2),15*sqrt((x(3)-17)^2+(x(4)-12)^2))+min(50*sqrt((x(1)-81)^2+(x(2)-63)^2),50*sqrt((x(3)-81)^2+(x(4)-63)^2))+min(8*sqrt((x(1)-19)^2+(x(2)-45)^2),8*sqrt((x(3)-19)^2+(x(4)-45)^2))+min(30*sqrt((x(1)-62)^2+(x(2)-12)^2),30*sqrt((x(3)-62)^2+(x(4)-12)^2));
%蒙特卡罗算法
MIN=inf;
%取一千万组随机数
LIMIT=10000000;
while LIMIT>0
%生成指定范围内的随机数
x(1)=82*rand;
x(2)=82*rand;
x(3)=82*rand;
x(4)=82*rand;
%过滤不符合条件的随机数
while x(1)>82 | x(1)<0 %| x(2)>81 | x(2)<0 | x
%再次生成随机数
x(1)=82*rand;
% x(2)=(1-0.9397)*rand+0.9397;
end;
while x(2)>82 | x(2)<0
x(2)=82*rand;
end;
while x(3)>82 | x(3)<0
x(3)=82*rand;
end;
while x(4)>82 | x(4)<0
x(4)=82*rand;
end;
temp=myobjfunc(x);
if temp<MIN
MIN=temp;
y=x;
end;
LIMIT=LIMIT-1;
end;
MIN
y
第三问结果:
利用蒙特卡洛算法matlab编程可求
程序多次运行的结果如下:
MIN =
6.5582e+003
y =
43.2099 25.0713 3.8432 81.0215
MIN =
6.5665e+003
y =
3.9281 81.0393 42.3370 27.9608
MIN =
6.5583e+003
y =
4.1848 81.1427 41.9258 25.2987
MIN =
6.5597e+003
y =
40.9820 25.7891 3.8891 80.8089
MIN =
6.5713e+003
y =
39.3252 23.5597 4.2433 80.8989
MIN =
6.5511e+003
y =
4.0086 81.1070 41.8500 25.6334
MIN =
6.5553e+003
y =
40.9798 26.6722 4.0593 80.9958
MIN =
6.5536e+003
y =
39.8126 24.6946 4.0317 81.0556
由多次运行程序的结果可知:
取其中最小的一次结果即可认为是本题求解答案:
MIN =6.5511e+003
y =4.0086 81.1070 41.8500 25.6334
即总费用最低为6551.1
两个炼油厂的坐标地址分别为(4.0086,81.1070),(41.8500,25.6334)
相关文章:

使用MATLAB解算炼油厂的选址
背景 记得有一年的数据建模大赛,试题是炼油厂的选址,最后我们采用MATLAB编写(复制)蒙特卡洛算法,还到了省级一等奖,这里把仅有一些记忆和材料,放到这里来,用来纪念消失的青春。 本…...

AudioTrack播放音乐之getMinBufferSize
1. AudioTrack播放音乐之前需要做好准备,即需要先计算最小音频数据缓存空间 文件路径:AudioTrack.java (frameworks\base\media\java\android\media) static public int getMinBufferSize(int sampleRateInHz, int channelConfig, int audioFormat) {@参数sampleRateInHz,…...

React和Redux中的不变性
https://overreacted.io/zh-hans/a-complete-guide-to-useeffect/ 一、不变性和副作用 1.不变:不断创造新值来替换旧值 2.不变性规则: (1)当给定相同的输入时,纯函数必须始终返回相同的值 (2࿰…...
NPM 常用命令(一)
目录 1、npm 1.1 简介 1.2 依赖性 1.3 安装方式 2、npm access 2.1 命令描述 2.2 详情 3、npm adduser 3.1 描述 4、npm audit 4.1 简介 4.2 审计签名 4.3 操作示例 4.4 配置 audit-level dry-run force json package-lock-only omit foreground-scripts …...

【ES6】Promise推荐用法
一般来说,不要在then()方法里面定义 Reject 状态的回调函数(即then的第二个参数),总是使用catch方法。 // bad promise.then(function(data) {// success}, function(err) {// error});// good promise.then(function(data) { //…...

【JavaScript】版本判断
用于客户端和服务端进行版本更新判断使用,如有BUG,还望指出 效果 console.log(isAllowUpdate(1,2.0.0), // trueisAllowUpdate(2.0,2.0.0), // falseisAllowUpdate(2.0,2.0.1), // trueisAllowUpdate(2.1.1,2.1.2), // trueisAllowUpdate(2.1.3,2.1.2),…...
Nano编辑器安装使用指南
关于nano Nano编辑器是一个命令行文本编辑器,具有简单易用的界面和一些基本功能。 Nano小巧友好,提供许多额外的特性,例如交互式的查找和替换、定位到指定的行列、自动缩进、特性切换、国际化支持、文件名标记完成等。 Nano是为了代替闭源的…...
Java版电子招投标管理系统源码-电子招投标认证服务平台-权威认证
项目说明 随着公司的快速发展,企业人员和经营规模不断壮大,公司对内部招采管理的提升提出了更高的要求。在企业里建立一个公平、公开、公正的采购环境,最大限度控制采购成本至关重要。符合国家电子招投标法律法规及相关规范,以及…...
Java String类(1)
String类的重要性 我们之前在C语言中已经涉及到字符串了,但是在C语言中要表示字符串只能使用字符数组或者字符指针,可以使用标准库提供的字符串系列函数完成大部分操作,但是这种将数据和操作数据的方法分离开的方式不符合面向对象的思想&…...
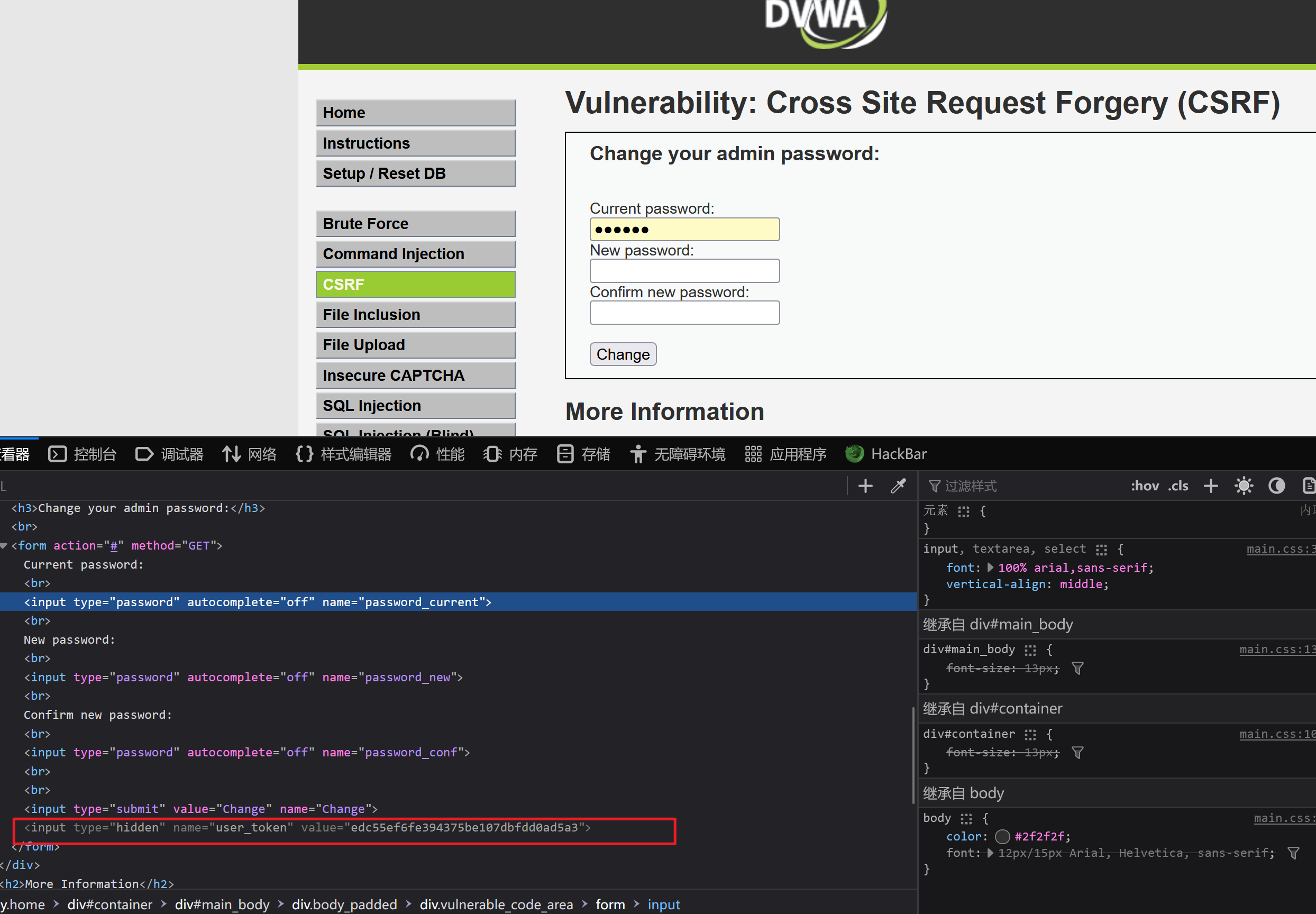
渗透测试漏洞原理之---【CSRF跨站请求伪造】
文章目录 1、CSRF概述1.1、基本原理1.1.1、基本概念1.1.2、关键点1.1.3、目标 1.2、CSRF场景1.2.1、银行支付转账1.2.2构造虚假网站1.2.3、场景建模 1.3、CSRF类别1.3.1、POST方式 1.4、CSRF验证1.4.1、CSRF PoC Generator 2、CSRF攻防2.1、CSRF实战2.1.1、与XSS 漏洞相结合 2.…...
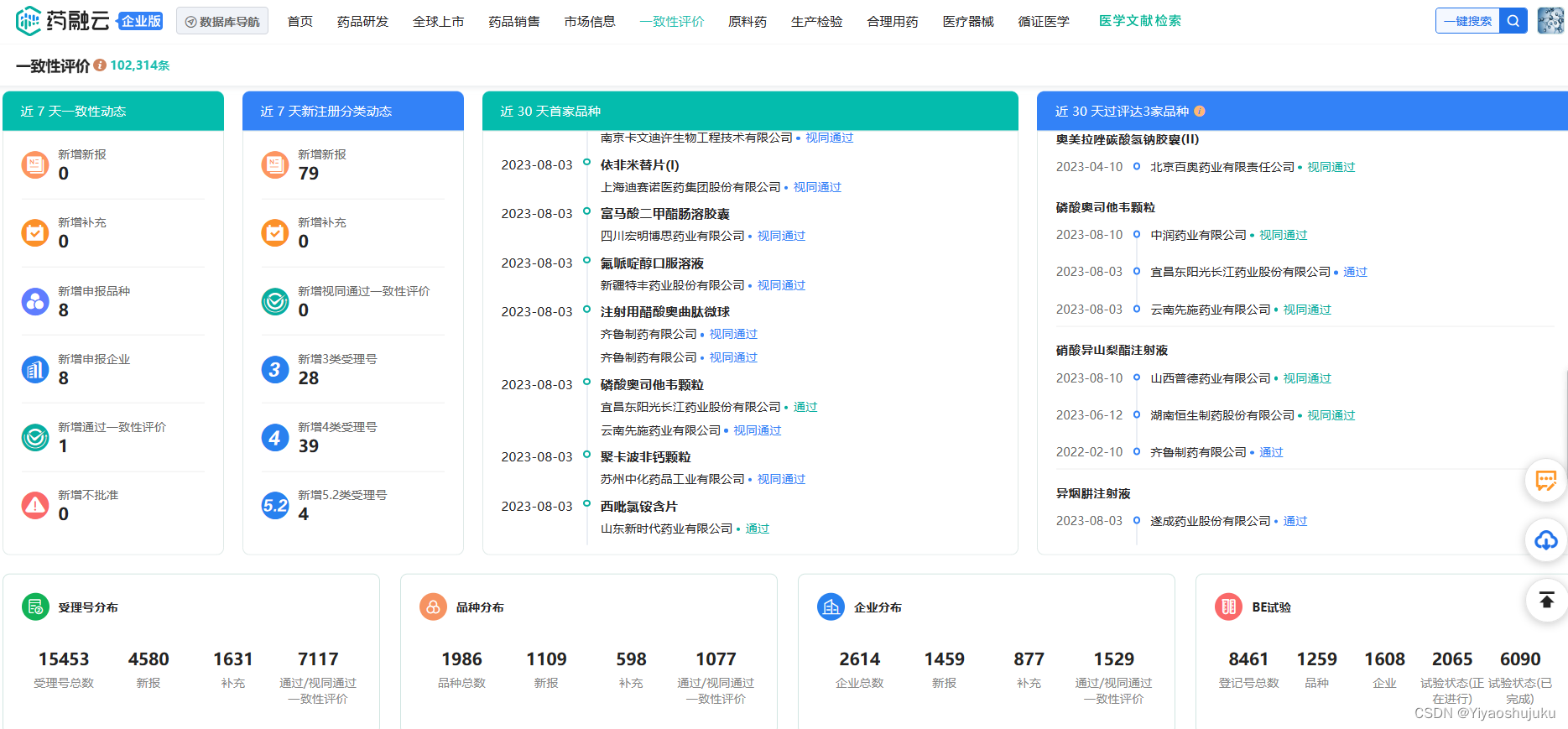
带量采购药品数据查询集采分析平台(建议收藏!)
药品集采常态化下对不同中标企业的影响不尽相同,对于市场份额较大且拥有多款重要药品的大型企业来说,集采能够保持其市场份额,尽管被集采的药品可能会面临销售下降的局面,但该企业还有其他产品可以填补,整体影响不大。…...

概念解析 | 无线感知的新篇章:异构网络感知的原理与挑战
注1:本文系“概念解析”系列之一,致力于简洁清晰地解释、辨析复杂而专业的概念。本次辨析的概念是:异构网络感知。 无线感知的新篇章:异构网络感知的原理与挑战 Interference Management in HetNets 在当今的无线通信领域,我们面临着一个重大的挑战:如何在有限的频谱资源…...
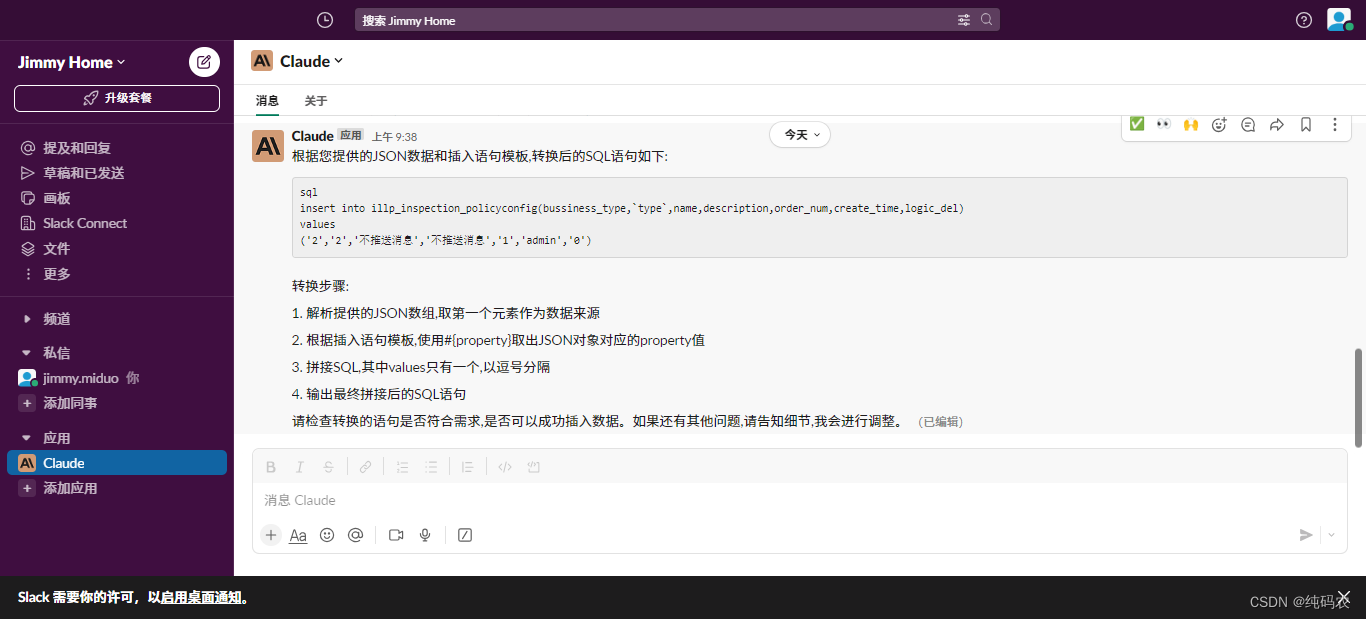
【大数据模型】让chatgpt为开发增速(开发专用提示词)
汝之观览,吾之幸也!本文主要聊聊怎样才能更好的使用提示词,给开发提速,大大缩减我们的开发时间,比如在开发中使用生成表结构脚本的提示词,生成代码的提示词等等。 一、准备 本文主要根据Claude进行演示&am…...

读书笔记-《ON JAVA 中文版》-摘要23[第二十章 泛型-2]
文章目录 第二十章 泛型5. 泛型擦除5.1 泛型擦除5.2 迁移兼容性5.3 擦除的问题5.4 边界处的动作 6. 补偿擦除7. 边界8. 通配符8.1 通配符8.2 逆变 9. 问题10. 动态类型安全11. 泛型异常 第二十章 泛型 普通的类和方法只能使用特定的类型:基本数据类型或类类型。如果…...
【爬虫】5.6 Selenium等待HTML元素
目录 任务目标 创建Ajax网站 创建服务器程序 Selenium XX 等待 1. Selenium强制等待 2. Selenium隐性等待 3. Selenium循环等待 4. Selenium显示等待 等待方法 任务目标 在浏览器加载网页的过程中,网页的有些元素时常会有延迟的现象,在HTML元素…...

0102阿里云配置3台ECS服务器-大数据学习
文章目录 1 前言1 配置VPC和子网2 创建安全组3 创建云服务器ECS3.1 规划配置3.2 配置 4 xshell连接服务器5 配置基础环境5.1 主机名映射5.2 ssh免密登录5.3 jdk 6 问题集6.1 Permission denied (publickey,gssapi-keyex,gssapi-with-mic).6.2 用tar解压文件出现错误Not found i…...
android 输入法demo
背景: 一个简单的android输入法demo,支持输入png、gif,jpeg、webp等格式。 此示例演示如何编写一个应用程序,该应用程序接受使用 Commit Content API 从键盘发送的丰富内容(例如图像)。 用户通常希望通过表…...

【经验分享】Markdown中如何显示空格和回车
Markdown中如何显示空格和回车 空格 利用html中的空格实体引用: eg: 这是一些 额外的空格。回车: 方法一:在你想要回车的地方连续按两次回车键 方法二:使用<br>标签 eg: 我想显示<br>…...

深入篇【C++】set和map(multiset/multimap)特性总结与使用
深入篇【C】set和map(multiset/multimap)特性总结与使用 一.set/multiset总结二.map/multiset总结三.set/map应用 一.set/multiset总结 set是按照一定次序存储元素的容器在set中,元素的value也标识它(value就是key,类型为T),并且每…...
OpenAI推出ChatGPT企业版,提供更高安全和隐私保障
🦉 AI新闻 🚀 OpenAI推出ChatGPT企业版,提供更高安全和隐私保障 摘要:OpenAI发布了面向企业用户的ChatGPT企业版,用户可以无限制地访问强大的GPT-4模型,进行更深入的数据分析,并且拥有完全控制…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
