图论(基础)
知识:
顶点,边 | 权,度数
1.图的种类:
有向图 | 无向图
有环 | 无环
联通性
基础1:图的存储(主要是邻接矩阵和邻接表)
例一:B3643 图的存储 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include <iostream>using namespace std;int n, m, d[1010];
bool edges[1010][1010];int main()
{cin >> n >> m;for(int i = 1; i <= m; i ++ ){int u, v;cin >> u >> v;edges[u][v] = true;edges[v][u] = true;}for(int i = 1; i <= n; i ++ ){for(int j = 1; j <= n; j ++ ){if(edges[i][j]) {cout << "1 ";d[i] ++;}else cout << "0 "; }cout << endl;}for(int i = 1; i <= n; i ++ ){cout << d[i] << ' ';for(int j = 1; j <= n; j ++ ){if(edges[i][j]) cout << j << ' ';}cout << endl;}return 0;
}例二:B3613 图的存储与出边的排序 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
该代码须加上快读快写
#include <iostream>
#include <set>
using namespace std;const int N = 5e5 + 10;
int n, m;
set<int> s[N];int main()
{int t;cin >> t;while(t -- ){cin >> n >> m;for(int i = 0; i < m; i ++ ){int a, b;cin >> a >> b;s[a].insert(b);}int j = 0;for(int i = 1; i <= n; i ++ ){for(auto it = s[i].begin(); it != s[i].end(); it ++ )cout << *it << ' ';cout << endl;}}return 0;
}图的遍历:通常是bfs()、dfs()
复习一下模板活动 - AcWing 活动 - AcWing
例一:P3916 图的遍历 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
因为是找最大值dfs,用了反向建边提高效率,用一个大值去标记多个小值
#include <iostream>
#include <cstring>
using namespace std;const int N = 1e5 + 10, M = 2 * N;
int n, m;
int e[N], ne[N], h[N], idx;
int res[N];void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}void dfs(int u, int maxn)
{res[u] = max(maxn, res[u]);for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(!res[j]) dfs(j, maxn);}
}int main()
{cin >> n >> m;memset(h, -1, sizeof h);while(m -- ){int u, v;cin >> u >> v;add(v, u);}for(int i = n; i >= 1; i -- ){//反向建边+遍历 有利于找最大值的效率// 如果是第一次被遍历到一定找到了遍历最大的值//已经被标记过最大值的说明他们下边的最大值也被标记过了if(res[i]) continue;dfs(i, i);}for(int i = 1; i <= n; i ++ ){cout << res[i] << ' ';}return 0;
}例二:活动 - AcWing 图的层次
肯定要用bfs啦
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int d[N];
int n,m;
queue<int> q;void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}int bfs()
{memset(d, -1, sizeof d);d[1] = 0;q.push(1);while(q.size()){auto t = q.front();q.pop();for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];if(d[j] == -1){d[j] = d[t] + 1;q.push(j);}}}return d[n];
}int main(){cin >> n >> m;memset(h, -1, sizeof h);for(int i = 0; i < m; i++ ){int a, b;cin >> a >> b;add(a, b);}cout << bfs() << endl;return 0;
}例三:P5318 【深基18.例3】查找文献 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
分别用dfs和bfs输出一遍。唯一的难点在于怎么做到 "如果有很多篇文章可以参阅,请先看编号较小的那篇(因此你可能需要先排序)。" 问题不大,排个序就行。
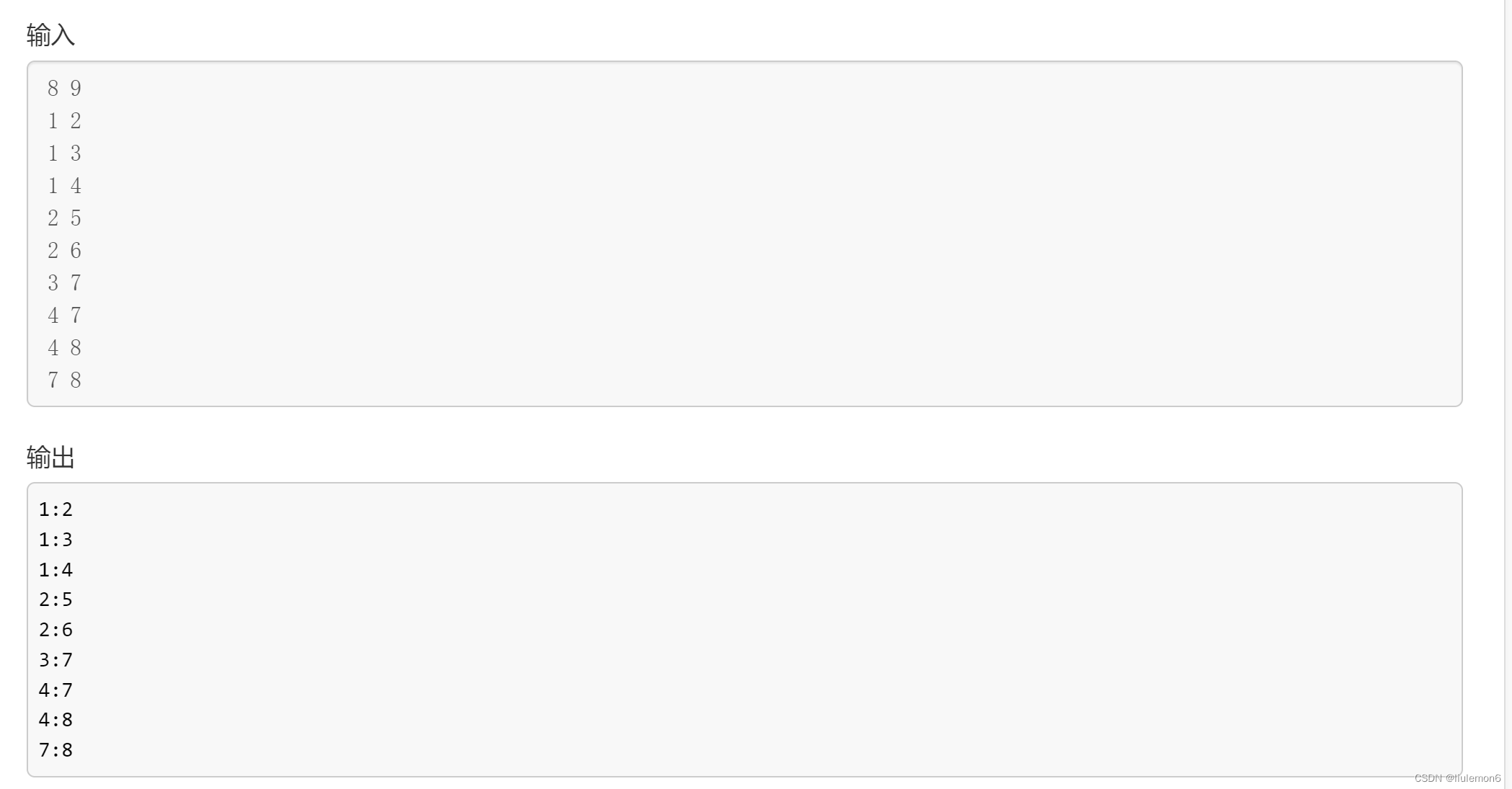
注意用邻接表存图(s存边先处理一下,即排序) 然后处理e[i][]表示i点连接的点
然后就是喜闻乐见的dfs递归一下,bfs一下
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;const int N = 1e5 + 10;
struct edges
{int a, b;
};
vector<int> e[N]; // e是邻接表,用来遍历
vector<edges> s; // 用来存边
int n, m;
bool st1[N], st2[N];
queue<int> q;bool cmp(edges x, edges y)
{//按照每条边终点从小到大排,终点相同的起点按从小到大排if(x.b == y.b) return x.a < y.a;else return x.b < y.b;
}void bfs()
{q.push(1);st2[1] = true;cout << '1' << ' ';while(q.size()){int t = q.front();q.pop();for(int i = 0; i < e[t].size(); i ++ ){int j = s[e[t][i]].b;if(!st2[j]){st2[j] = true;cout << j << ' ';q.push(j);}}}
}
void dfs(int u)
{st1[u] = true;cout << u << ' ';for(int i = 0; i < e[u].size(); i ++ ){int j = s[e[u][i]].b;if(!st1[j]) dfs(j);}
}int main()
{cin >> n >> m;for(int i = 0; i < m; i ++ ){int a, b;cin >> a >> b;s.push_back((edges){a, b});}sort(s.begin(), s.end(), cmp);//m条边放到e中 for(int i = 0; i < m; i ++ ){e[s[i].a].push_back(i); // e存某个点到其他点的边的编号}// for(int i = 0; i < m; i ++ )// {// cout << s[i].a << ':' << s[i].b << endl;// }dfs(1);puts("");bfs();return 0;
}相关文章:

图论(基础)
知识: 顶点,边 | 权,度数 1.图的种类: 有向图 | 无向图 有环 | 无环 联通性 基础1:图的存储(主要是邻接矩阵和邻接表) 例一:B3643 图的存储 - 洛谷 | 计算机科学教育新生态 (…...

docker的运行原理
Docker 是一个开源的容器化技术,它能够让开发者将应用及其依赖打包到一个轻量级的、可移植的容器中,这个容器可以在几乎任何机器上一致地运行。要了解 Docker 的运行原理,我们首先要理解以下几个核心概念: 容器 (Container): 容器是一个轻量级的、独立的、可执行的软件包,…...
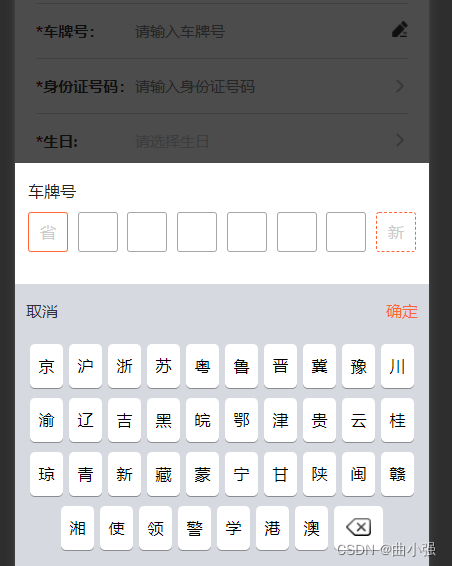
vue自定义键盘
<template><div class"mark" click"isOver"></div><div class"mycar"><div class"mycar_list"><div class"mycar_list_con"><p class"mycar_list_p">车牌号</p>…...
k8s 安装 kubernetes安装教程 虚拟机安装k8s centos7安装k8s kuberadmin安装k8s k8s工具安装 k8s安装前配置参数
k8s采用master, node1, node2 。三台虚拟机安装的一主两从,机器已提前安装好docker。下面是机器配置,k8s安装过程,以及出现的问题与解决方法 虚拟机全部采用静态ip, master 30机器, node1 31机器, node2 32机器 机器ip 192.168.164.30 # ma…...

2023年高教社杯数学建模思路 - 案例:感知机原理剖析及实现
文章目录 1 感知机的直观理解2 感知机的数学角度3 代码实现 4 建模资料 # 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 感知机的直观理解 感知机应该属于机器学习算法中最简单的一种算法,其…...
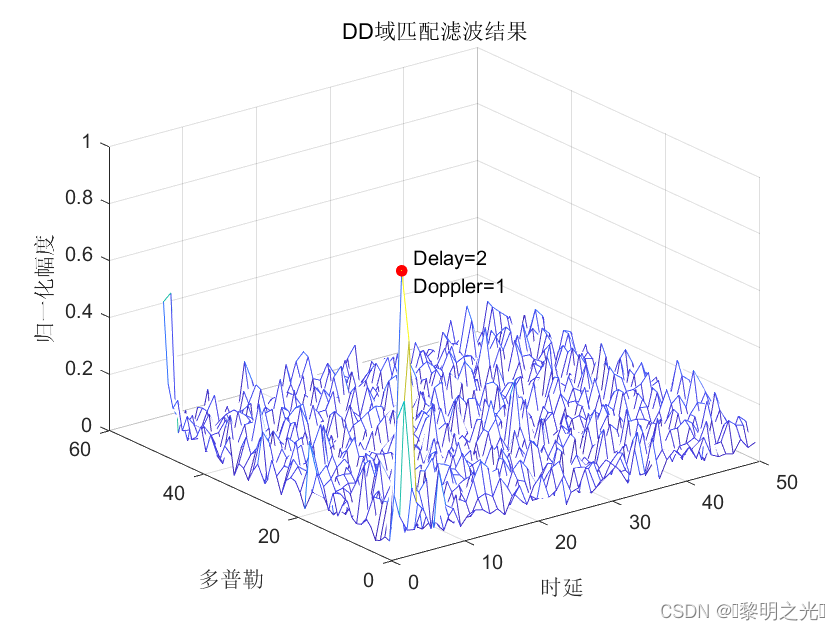
OTFS-ISAC雷达部分最新进展(含matlab仿真+USRP验证)
OTFS基带参数设置 我将使用带宽为80MHz的OTFS波形进行设计,对应参数如下: matlab Tx仿真 Tx导频Tx功率密度谱 帧结构我使用的是经典嵌入导频帧结构,Tx信号波形的带宽从右图可以看出约为80Mhz USRP验证 测试环境 无人机位于1m处 Rx导频Rx…...
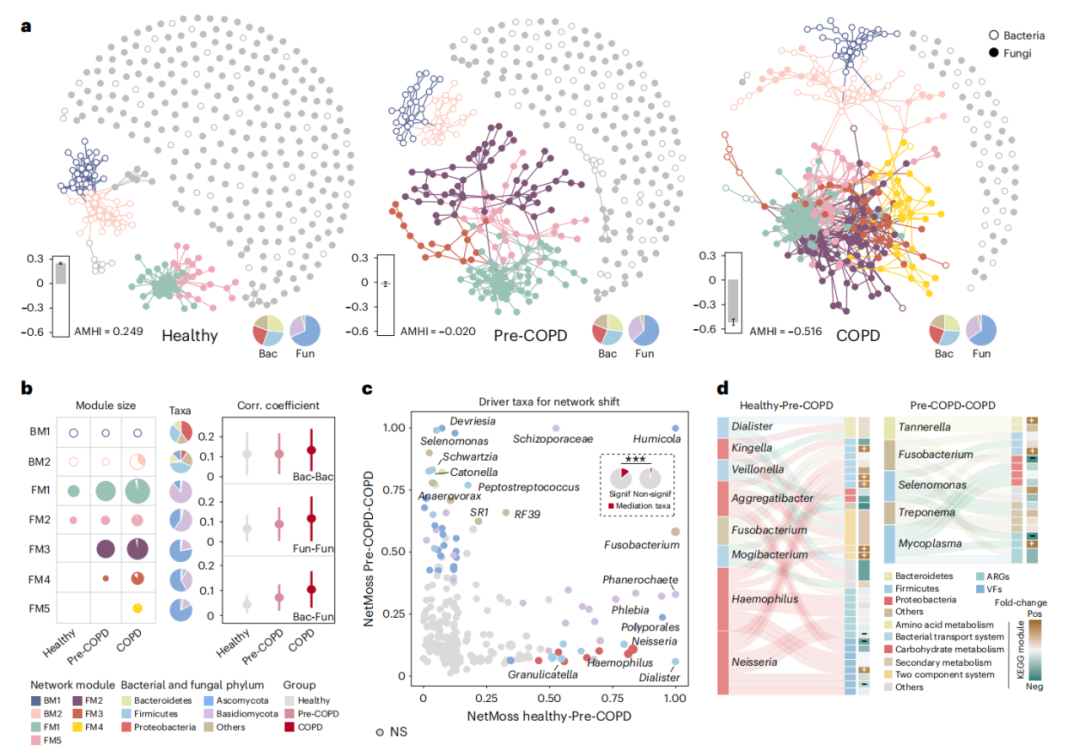
Cell | 超深度宏基因组!复原消失的肠道微生物
期刊:Cell IF:64.5 (Q1) 发表时间:2023.6 研究背景 不同的生活方式会影响微生物组组成,但目前微生物组的研究严重偏向于西方工业化人群,其中工业化人群的特点是微生物群多样性较低。为了理解工…...

Centos7 设置代理方法
针对上面变量的设置方法: 1、在/etc/profile文件 2、在~/.bashrc 3、在~/.zshrc 4、在/etc/profile.d/文件夹下新建一个文件xxx.sh 写入如下配置: export proxy"http://192.168.5.14:8118" export http_proxy$proxy export https_proxy$pro…...
)
Android versions (Android 版本)
Android versions (Android 版本) All Android releases https://developer.android.com/about/versions Android 1.0 G1 Android 1.5 Cupcake Android 1.6 Donut Android 2.0 Eclair Android 2.2 Froyo Android 2.3 Gingerbread Android 3.0 Honeycomb Android 4.0 Ic…...
LNMP 平台搭建(四十)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 搭建LNMP 一、安装Nginx 二、安装Mysql 三、安装PHP 四、部署应用 前言 LNMP平台指的是将Linux、Nginx、MySQL和PHP(或者其他的编程语言,如…...

pcie 6.0/7.0相对pcie 5.0的变化有哪些?
引言 话说,小编在CSDN博客跟客服机器人聊天,突然看到有个搜索热搜“pcie最全科普贴”。小编有点似曾相识呀,我就好奇点击了一下,没想到几年前写的帖子在CSDN又火了一把。 说到这里,顺带给自己打个广告哈~ …...

百度Apollo:自动驾驶技术的未来应用之路
文章目录 前言一、城市交通二、出行体验三、环境保护四、未来前景总结 前言 随着科技的不断进步,自动驾驶技术正逐渐成为现实,颠覆着我们的出行方式。作为中国领先的自动驾驶平台,百度Apollo以其卓越的技术和开放的合作精神,正在…...

C++之std::distance应用实例(一百八十八)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

中国建筑出版传媒许少辉八一新书乡村振兴战略下传统村落文化旅游设计日
中国建筑出版传媒许少辉八一新书乡村振兴战略下传统村落文化旅游设计日...
基于java Swing 和 mysql实现的购物管理系统(源码+数据库+说明文档+运行指导视频)
一、项目简介 本项目是一套基于java Swing 和 mysql实现的购物管理系统,主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的Java学习者。 包含:项目源码、项目文档、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过…...

2023.9 - java - static 关键字
static关键字主要和Java的内存管理有关。我们可以将static关键字与变量,方法,代码块一起使用。static关键字属于该类,而不是该类的实例。 static关键字可以修饰: 变量(也称为类变量)方法(也称…...

SpringCloud学习笔记(十二)_Zipkin全链路监控
Zipkin是SpringCloud官方推荐的一款分布式链路监控的组件,使用它我们可以得知每一个请求所经过的节点以及耗时等信息,并且它对代码无任何侵入,我们先来看一下Zipkin给我们提供的UI界面都是提供了哪些信息。 如何使用Zipkin 虽然在SpringBoot…...
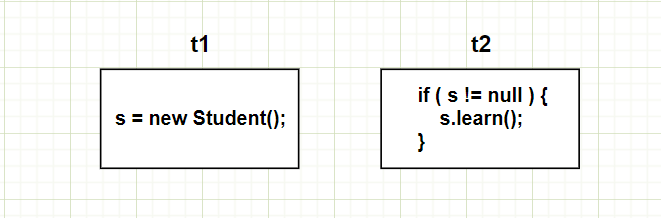
Java 多线程系列Ⅱ(线程安全)
线程安全 一、线程不安全线程不安全的原因: 二、线程不安全案例与解决方案1、修改共享资源synchronized 使用synchronized 特性 2、内存可见性Java内存模型(JMM)内存可见性问题 3、指令重排列4、synchronized 和 volatile5、拓展知识…...

const用法详解
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、const用法详解二、使用步骤 1.引入库2.读入数据总结 前言 提示:这里可以添加本文要记录的大概内容: 例如:随着人工智能…...
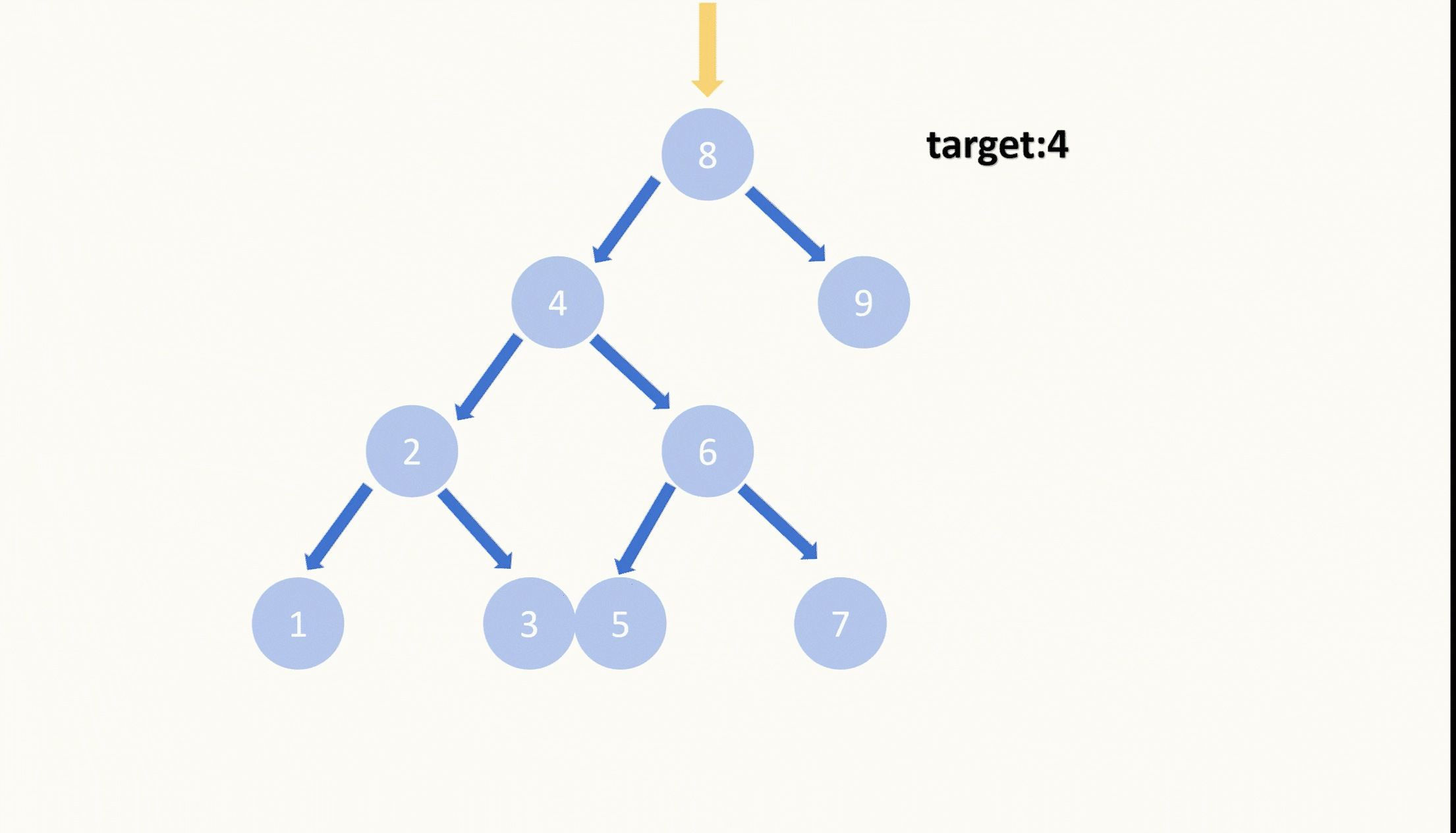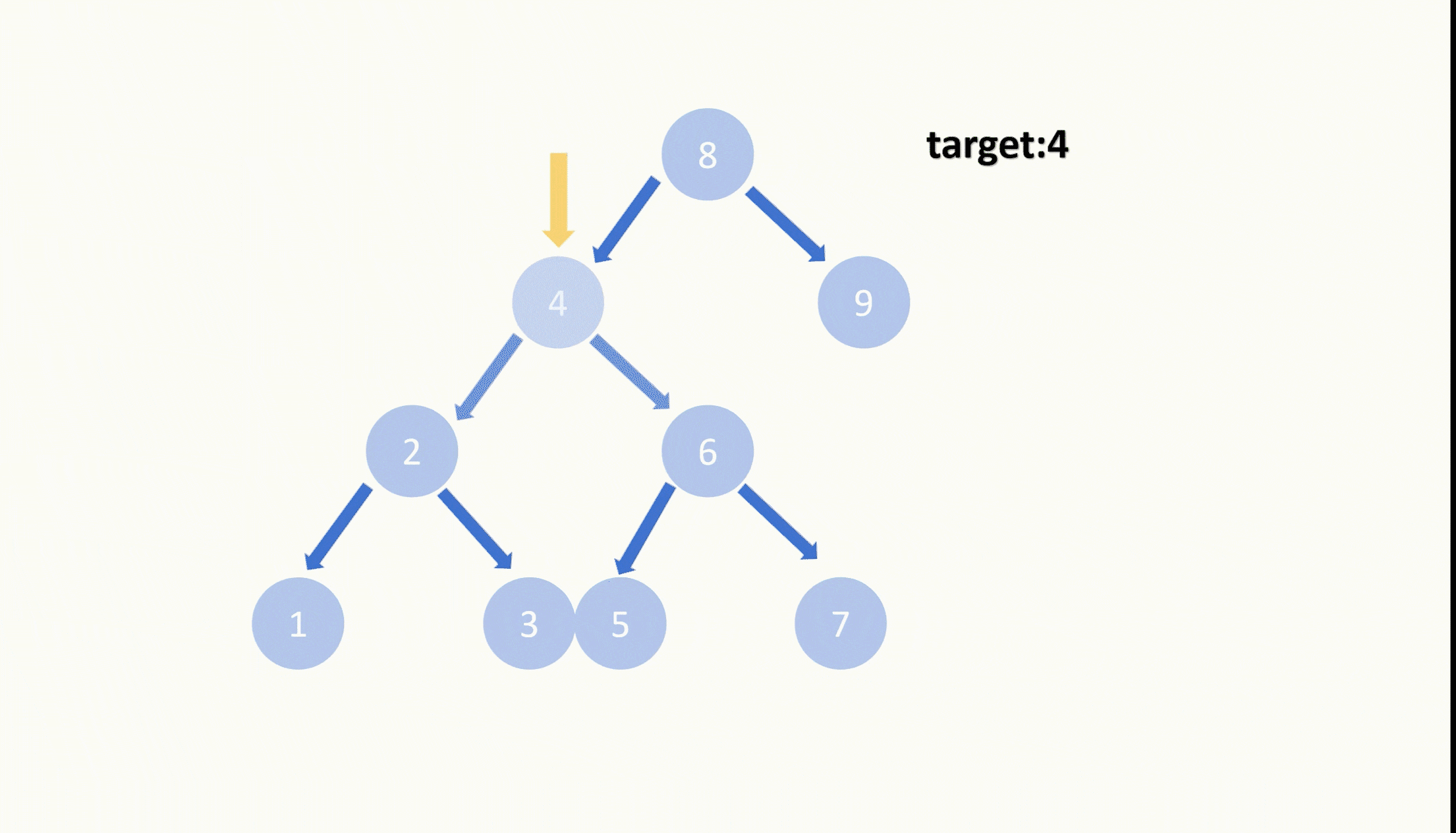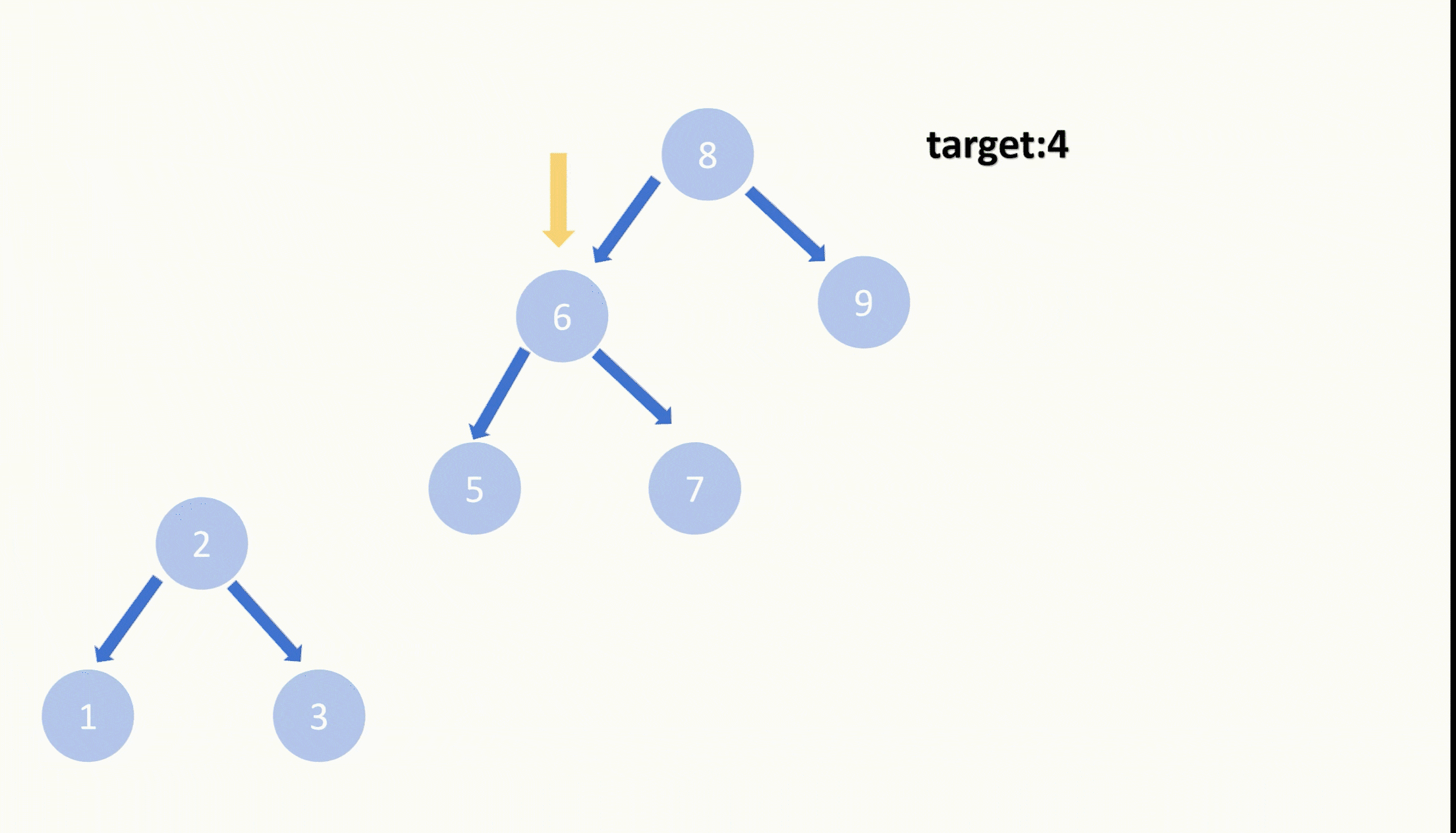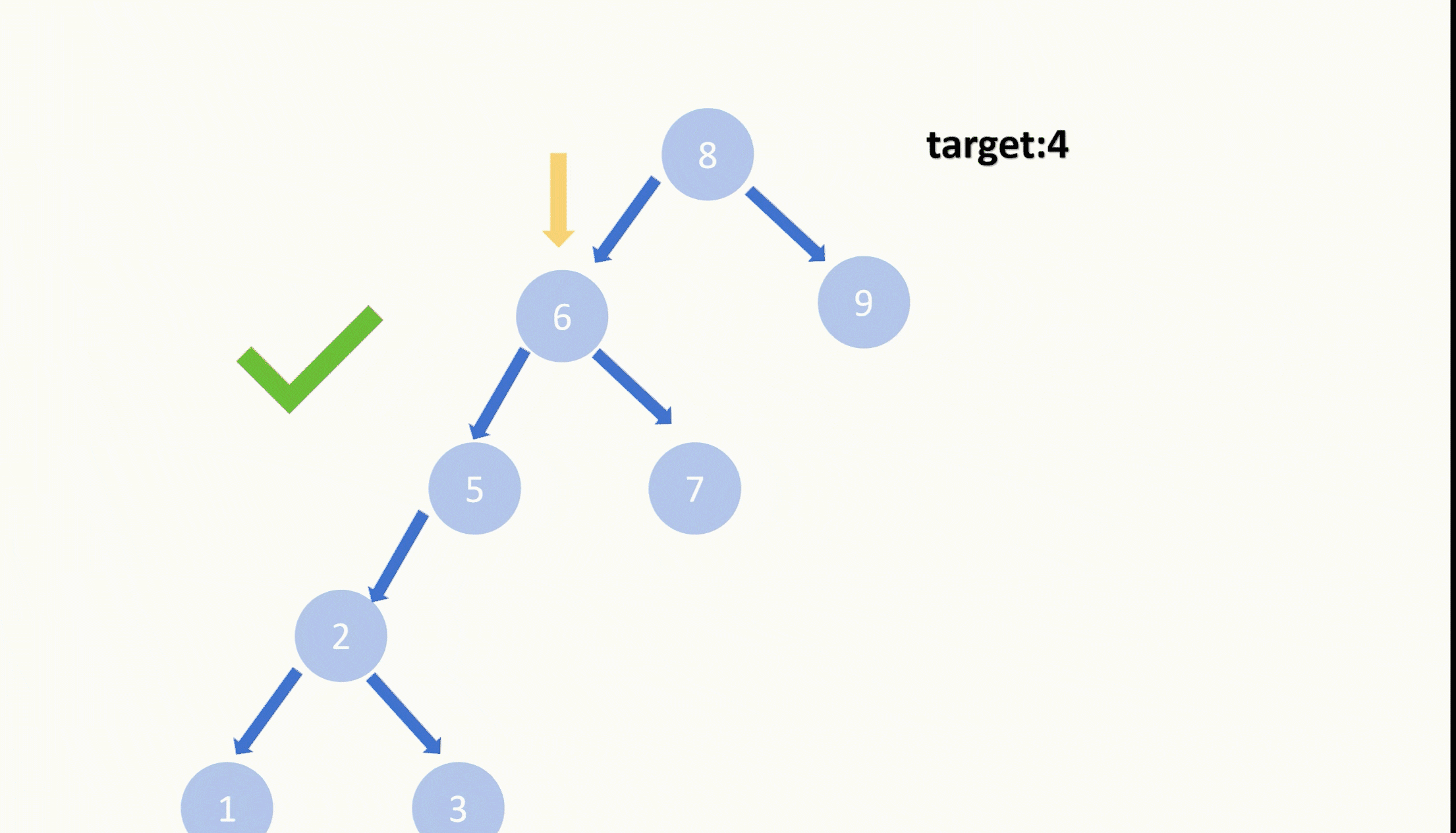
【LeetCode75】第四十二题 删除二叉搜索数中的节点
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们一棵二叉搜索树,给我们一个目标值,让我们删除节点值等于目标值的节点,并且删除之后需要保持…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
