22.2.19周赛双周赛(贪心、记忆化搜索...)
文章目录
- 双周赛98
- [6359. 替换一个数字后的最大差值](https://leetcode.cn/problems/maximum-difference-by-remapping-a-digit/)
- [6361. 修改两个元素的最小分数](https://leetcode.cn/problems/minimum-score-by-changing-two-elements/)
- 贪心+排序
- [6360. 最小无法得到的或值](https://leetcode.cn/problems/minimum-impossible-or/)
- [6358. 更新数组后处理求和查询](https://leetcode.cn/problems/handling-sum-queries-after-update/)
- 周赛333
- [6362. 合并两个二维数组 - 求和法](https://leetcode.cn/problems/merge-two-2d-arrays-by-summing-values/)
- [6365. 将整数减少到零需要的最少操作数](https://leetcode.cn/problems/minimum-operations-to-reduce-an-integer-to-0/)
- 记忆化搜索
0x3f:从周赛中学算法 - 2022 年周赛题目总结(下篇)https://leetcode.cn/circle/discuss/WR1MJP/
- 模拟
- 技巧
- 动态规划
- 数据结构
- 图论
- 数学
- 思维题
双周赛98
6359. 替换一个数字后的最大差值
难度简单1
给你一个整数 num 。你知道 Danny Mittal 会偷偷将 0 到 9 中的一个数字 替换 成另一个数字。
请你返回将 num 中 恰好一个 数字进行替换后,得到的最大值和最小值的差位多少。
注意:
- 当 Danny 将一个数字
d1替换成另一个数字d2时,Danny 需要将nums中所有d1都替换成d2。 - Danny 可以将一个数字替换成它自己,也就是说
num可以不变。 - Danny 可以将数字分别替换成两个不同的数字分别得到最大值和最小值。
- 替换后得到的数字可以包含前导 0 。
- Danny Mittal 获得周赛 326 前 10 名,让我们恭喜他。
示例 1:
输入:num = 11891
输出:99009
解释:
为了得到最大值,我们将数字 1 替换成数字 9 ,得到 99899 。
为了得到最小值,我们将数字 1 替换成数字 0 ,得到 890 。
两个数字的差值为 99009 。
示例 2:
输入:num = 90
输出:99
解释:
可以得到的最大值是 99(将 0 替换成 9),最小值是 0(将 9 替换成 0)。
所以我们得到 99 。
提示:
1 <= num <= 108
class Solution {public int minMaxDifference(int num) {String str = num + "";String max = str, min = str;for(int i = 0; i < str.length(); i++){if(str.charAt(i) != '9'){max = str.replace(str.charAt(i),'9');break;}}for(int i = 0; i < str.length(); i++){if(str.charAt(i) != '0'){min = str.replace(str.charAt(i), '0');break;}}return Integer.parseInt(max) - Integer.parseInt(min);}
}
class Solution {public int minMaxDifference(int num) {String str = num + "";char a = str.charAt(0), b = ' ';boolean flag = false;for(int i = 0; i < str.length(); i++){char c = str.charAt(i);if(c != '9'){flag = true;b = c;break;}}String min = str.replace(a, '0');String max = flag ? str.replace(b, '9') : str;return Integer.parseInt(max) - Integer.parseInt(min);}
}
6361. 修改两个元素的最小分数
难度中等5
给你一个下标从 0 开始的整数数组 nums 。
nums的 最小 得分是满足0 <= i < j < nums.length的|nums[i] - nums[j]|的最小值。nums的 最大 得分是满足0 <= i < j < nums.length的|nums[i] - nums[j]|的最大值。nums的分数是 最大 得分与 最小 得分的和。
我们的目标是最小化 nums 的分数。你 最多 可以修改 nums 中 2 个元素的值。
请你返回修改 nums 中 至多两个 元素的值后,可以得到的 最小分数 。
|x| 表示 x 的绝对值。
示例 1:
输入:nums = [1,4,3]
输出:0
解释:将 nums[1] 和 nums[2] 的值改为 1 ,nums 变为 [1,1,1] 。|nums[i] - nums[j]| 的值永远为 0 ,所以我们返回 0 + 0 = 0 。
示例 2:
输入:nums = [1,4,7,8,5]
输出:3
解释:
将 nums[0] 和 nums[1] 的值变为 6 ,nums 变为 [6,6,7,8,5] 。
最小得分是 i = 0 且 j = 1 时得到的 |nums[i] - nums[j]| = |6 - 6| = 0 。
最大得分是 i = 3 且 j = 4 时得到的 |nums[i] - nums[j]| = |8 - 5| = 3 。
最大得分与最小得分之和为 3 。这是最优答案。
提示:
3 <= nums.length <= 1051 <= nums[i] <= 109
贪心+排序
class Solution {//排序 + 贪心,本质是求修改后数组的最大差最小是多少。//左边修改两个最小的变成第三小,右边修改两个大最大的变成第三大,左右各修改一个最大最小public int minimizeSum(int[] nums) {// 最小的得分和,就要求所有的数尽量的小Arrays.sort(nums);// 最小得分一定可以是0// 三种情况int ans = 0x7f7f7f7f;int n = nums.length;// 一头一尾ans = Math.min(ans, nums[n - 2] - nums[1]);// 两头ans = Math.min(ans, nums[n - 1] - nums[2]);// 两尾ans = Math.min(ans, nums[n - 3] - nums[0]);return ans;}
}
6360. 最小无法得到的或值
难度中等6
给你一个下标从 0 开始的整数数组 nums 。
如果存在一些整数满足 0 <= index1 < index2 < ... < indexk < nums.length ,得到 nums[index1] | nums[index2] | ... | nums[indexk] = x ,那么我们说 x 是 可表达的 。换言之,如果一个整数能由 nums 的某个子序列的或运算得到,那么它就是可表达的。
请你返回 nums 不可表达的 最小非零整数 。
示例 1:
输入:nums = [2,1]
输出:4
解释:1 和 2 已经在数组中,因为 nums[0] | nums[1] = 2 | 1 = 3 ,所以 3 是可表达的。由于 4 是不可表达的,所以我们返回 4 。
示例 2:
输入:nums = [5,3,2]
输出:1
解释:1 是最小不可表达的数字。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 109
或操作越或越大
class Solution {public int minImpossibleOR(int[] nums) {// 脑经急转弯// 第一个不在nums中的2的幂// 如果2^1, ... , 2^k都在// 那么可以表示所有1...2^(k + 1) - 1的数Set<Integer> set = new HashSet<>();for(int i : nums){set.add(i);}for(int i = 0; i < 32; i++){if(!set.contains(1 << i)) return 1 << i;}return -1;}
}
6358. 更新数组后处理求和查询
难度困难5
给你两个下标从 0 开始的数组 nums1 和 nums2 ,和一个二维数组 queries 表示一些操作。总共有 3 种类型的操作:
- 操作类型 1 为
queries[i] = [1, l, r]。你需要将nums1从下标l到下标r的所有0反转成1或将1反转成0。l和r下标都从 0 开始。 - 操作类型 2 为
queries[i] = [2, p, 0]。对于0 <= i < n中的所有下标,令nums2[i] = nums2[i] + nums1[i] * p。 - 操作类型 3 为
queries[i] = [3, 0, 0]。求nums2中所有元素的和。
请你返回一个数组,包含所有第三种操作类型的答案。
示例 1:
输入:nums1 = [1,0,1], nums2 = [0,0,0], queries = [[1,1,1],[2,1,0],[3,0,0]]
输出:[3]
解释:第一个操作后 nums1 变为 [1,1,1] 。第二个操作后,nums2 变成 [1,1,1] ,所以第三个操作的答案为 3 。所以返回 [3] 。
示例 2:
输入:nums1 = [1], nums2 = [5], queries = [[2,0,0],[3,0,0]]
输出:[5]
解释:第一个操作后,nums2 保持不变为 [5] ,所以第二个操作的答案是 5 。所以返回 [5] 。
提示:
1 <= nums1.length,nums2.length <= 105nums1.length = nums2.length1 <= queries.length <= 105queries[i].length = 30 <= l <= r <= nums1.length - 10 <= p <= 1060 <= nums1[i] <= 10 <= nums2[i] <= 109
//有错不想调试了,后面复习线段树
class Solution {/**操作类型1:lazy更新 : 0 表示不需要更新 != 0 表示需要更新*/public long[] handleQuery(int[] nums1, int[] nums2, int[][] queries) {int n = nums1.length;List<Long> ans = new ArrayList<>();long sum = 0;for(int x :nums2) sum += x;buildTree(root, 0,n-1, nums1);for(int[] q : queries){if(q[0] == 1) update(root, 0, N, q[1], q[2]);else if(q[0] == 2) sum += q[1] * 1L * sum();else ans.add(sum);}return ans.stream().mapToLong(Long::valueOf).toArray();}class Node {Node left, right;int val, add;}private int N = (int) 1e9;private Node root = new Node();public void buildTree(Node node, int start, int end, int[] nums1) {// 到达叶子节点if (start == end) {node.val = nums1[start];return ;}int mid = (start + end) >> 1;node.left = new Node();node.right = new Node();buildTree(node.left, start, mid, nums1);buildTree(node.right, mid + 1, end, nums1);// 向上更新pushUp(node);}//初始值start和end是固定的0-N,l和r是要更新的区间,更新值为valpublic void update(Node node, int start, int end, int l, int r) {if (l <= start && end <= r) {//node.val += (end - start + 1) * val;node.val = end - start + 1 - node.val;node.add = 1;return;}int mid = (start + end) >> 1;pushDown(node, mid - start + 1, end - mid, mid);if (l <= mid) update(node.left, start, mid, l, r);if (r > mid) update(node.right, mid + 1, end, l, r);pushUp(node);}public int query(Node node, int start, int end, int l, int r) {if (l <= start && end <= r) return node.val;int mid = (start + end) >> 1, ans = 0;pushDown(node, mid - start + 1, end - mid, mid);if (l <= mid) ans += query(node.left, start, mid, l, r);if (r > mid) ans += query(node.right, mid + 1, end, l, r);return ans;}private void pushUp(Node node) {node.val = node.left.val + node.right.val;}private void pushDown(Node node, int leftNum, int rightNum, int mid) {if (node.left == null) node.left = new Node();if (node.right == null) node.right = new Node();if (node.add == 0) return ;node.left.val += mid - leftNum - node.val;node.right.val += rightNum - mid - node.val;// 对区间进行「加减」的更新操作,下推懒惰标记时需要累加起来,不能直接覆盖node.left.add = 1;node.right.add = 1;node.add = 0;}private int sum(){return root.val;}
}
周赛333
6362. 合并两个二维数组 - 求和法
难度简单2
给你两个 二维 整数数组 nums1 和 nums2.
nums1[i] = [idi, vali]表示编号为idi的数字对应的值等于vali。nums2[i] = [idi, vali]表示编号为idi的数字对应的值等于vali。
每个数组都包含 互不相同 的 id ,并按 id 以 递增 顺序排列。
请你将两个数组合并为一个按 id 以递增顺序排列的数组,并符合下述条件:
- 只有在两个数组中至少出现过一次的 id 才能包含在结果数组内。
- 每个 id 在结果数组中 只能出现一次 ,并且其对应的值等于两个数组中该 id 所对应的值求和。如果某个数组中不存在该 id ,则认为其对应的值等于
0。
返回结果数组。返回的数组需要按 id 以递增顺序排列。
示例 1:
输入:nums1 = [[1,2],[2,3],[4,5]], nums2 = [[1,4],[3,2],[4,1]]
输出:[[1,6],[2,3],[3,2],[4,6]]
解释:结果数组中包含以下元素:
- id = 1 ,对应的值等于 2 + 4 = 6 。
- id = 2 ,对应的值等于 3 。
- id = 3 ,对应的值等于 2 。
- id = 4 ,对应的值等于5 + 1 = 6 。
示例 2:
输入:nums1 = [[2,4],[3,6],[5,5]], nums2 = [[1,3],[4,3]]
输出:[[1,3],[2,4],[3,6],[4,3],[5,5]]
解释:不存在共同 id ,在结果数组中只需要包含每个 id 和其对应的值。
提示:
1 <= nums1.length, nums2.length <= 200nums1[i].length == nums2[j].length == 21 <= idi, vali <= 1000- 数组中的 id 互不相同
- 数据均按 id 以严格递增顺序排列
class Solution {public int[][] mergeArrays(int[][] nums1, int[][] nums2) {List<int[]> list = new ArrayList<>();int i = 0, j = 0;while(i < nums1.length && j < nums2.length){int key = 0, val = 0;if(nums1[i][0] == nums2[j][0]){val = nums1[i][1] + nums2[j][1];key = nums1[i][0];i++; j++;}else if(nums1[i][0] < nums2[j][0]){val = nums1[i][1];key = nums1[i][0];i++;}else{val = nums2[j][1];key = nums2[j][0];j++;}list.add(new int[]{key, val});}if(i != nums1.length){while(i != nums1.length){list.add(new int[]{nums1[i][0], nums1[i][1]});i++;}}if(j != nums2.length){while(j != nums2.length){list.add(new int[]{nums2[j][0], nums2[j][1]});j++;}}int[][] res = new int[list.size()][2];for(int k = 0; k < list.size(); k++){res[k][0] = list.get(k)[0];res[k][1] = list.get(k)[1];}return res;}
}
6365. 将整数减少到零需要的最少操作数
难度简单11
给你一个正整数 n ,你可以执行下述操作 任意 次:
n加上或减去2的某个 幂
返回使 n 等于 0 需要执行的 最少 操作数。
如果 x == 2i 且其中 i >= 0 ,则数字 x 是 2 的幂。
示例 1:
输入:n = 39
输出:3
解释:我们可以执行下述操作:
- n 加上 20 = 1 ,得到 n = 40 。
- n 减去 23 = 8 ,得到 n = 32 。
- n 减去 25 = 32 ,得到 n = 0 。
可以证明使 n 等于 0 需要执行的最少操作数是 3 。
示例 2:
输入:n = 54
输出:3
解释:我们可以执行下述操作:
- n 加上 21 = 2 ,得到 n = 56 。
- n 加上 23 = 8 ,得到 n = 64 。
- n 减去 26 = 64 ,得到 n = 0 。
使 n 等于 0 需要执行的最少操作数是 3 。
提示:
1 <= n <= 105
记忆化搜索
class Solution {Map<Integer, Integer> map = new HashMap<>();public int minOperations(int n) {return dfs(n);}public int dfs(int x){if((x & (x-1)) == 0) return 1;if(map.containsKey(x)) return map.get(x);int lowbit = x & -x;int cur = 1 + Math.min(dfs(x + lowbit), dfs(x - lowbit));map.put(x, cur);return cur;}
}
,得到 n = 0 。
使 n 等于 0 需要执行的最少操作数是 3 。
**提示:**- `1 <= n <= 105`### 记忆化搜索```java
class Solution {Map<Integer, Integer> map = new HashMap<>();public int minOperations(int n) {return dfs(n);}public int dfs(int x){if((x & (x-1)) == 0) return 1;if(map.containsKey(x)) return map.get(x);int lowbit = x & -x;int cur = 1 + Math.min(dfs(x + lowbit), dfs(x - lowbit));map.put(x, cur);return cur;}
}
相关文章:
)
22.2.19周赛双周赛(贪心、记忆化搜索...)
文章目录双周赛98[6359. 替换一个数字后的最大差值](https://leetcode.cn/problems/maximum-difference-by-remapping-a-digit/)[6361. 修改两个元素的最小分数](https://leetcode.cn/problems/minimum-score-by-changing-two-elements/)贪心排序[6360. 最小无法得到的或值](ht…...
2023最新软件测试面试题(带答案)
1. 请自我介绍一下(需简单清楚的表述自已的基本情况,在这过程中要展现出自信,对工作有激情,上进,好学) 面试官您好,我叫###,今年26岁,来自江西九江,就读专业是电子商务,毕…...
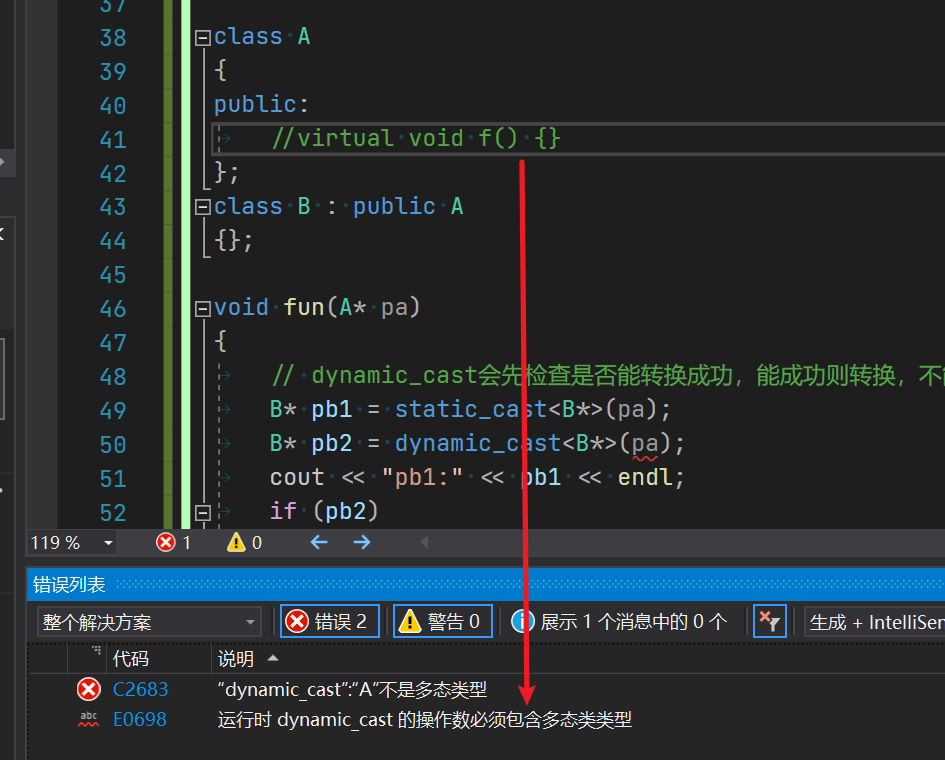
【C++】类型转换方法
本篇博客让我们来见识一下C中新增的类型转换方法 文章目录1.C语言中类型转换2.C中的强制类型转换2.1 static_cast2.2 reinterpret_cast2.3 const_castvolatile关键字2.4 dynamic_cast3.C强制类型转换的作用4.RTTI1.C语言中类型转换 在C语言中,类型转换有下面两种形…...

100亿级订单怎么调度,来一个大厂的极品方案
背景 超时处理,是一个很有技术难度的问题。 所以很多的小伙伴,在写简历的时候,喜欢把这个技术难题写在简历里边, 体现自己高超的技术水平。 在40岁老架构师 尼恩的读者交流群(50)中,尼恩经常指导大家 优化简历。 最…...
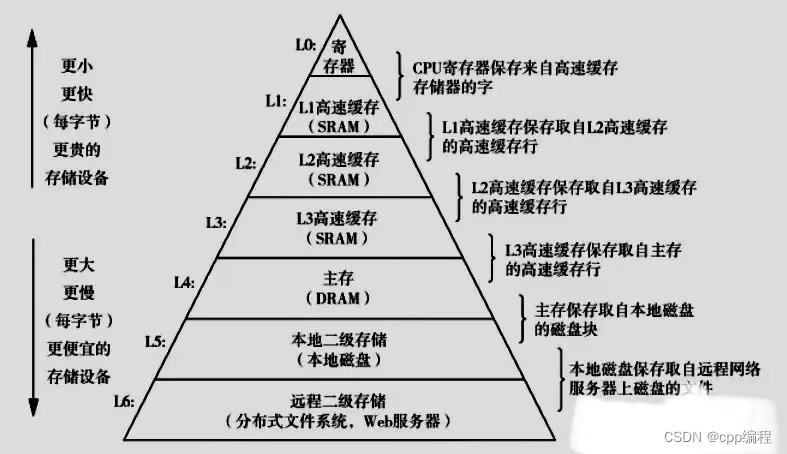
C++性能白皮书
最近看完了《C性能白皮书》,这本书列出了一些性能优化的思路,不过只是一些指引,没有讲具体细节,我整理出了其中的关键点分享给大家: 硬件篇 作为一个程序员,想要性能优化,最好要了解些硬件&…...

华为OD机试 - 黑板上色 | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 简易压缩算法(Python) | 机试题算法思路 【2023】 华为OD机试题 - 获取最大软件版本号(JavaScript) 华为OD机试 - 猜字谜(Python) | 机试题+算法思路 【2023】 华为OD机试 - 删除指定目录(Python) | 机试题算法思路 【2023】 华为OD机试 …...

如何在六秒内吸引观众的注意力
根据《2022国民专注力洞察报告》显示,当代人的连续专注时长,已经从2000年的12秒,下降到了现在的8秒。对于这个事实你可能难以相信,实际上这意味着,大多数互联网用户跳到一些页面上时,可能眼皮都不眨一下就离…...
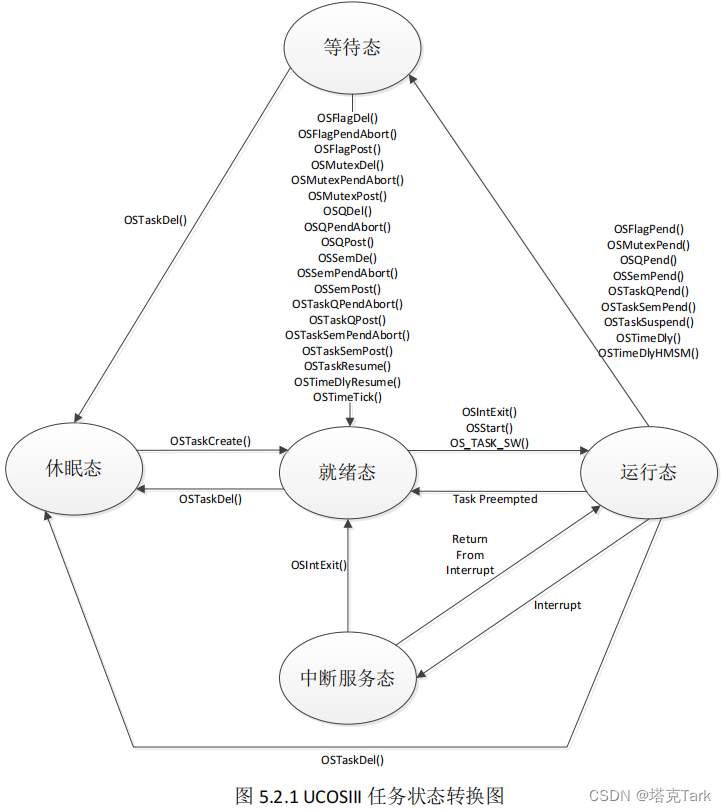
FreeRTOS与UCOSIII任务状态对比
FreeRTOS任务状态 1、运行态 正在运行的任务,正在使用处理器的任务。 单核处理器中任何时候都有且只有一个任务处于运行态。 2、就绪态 已经准备就绪(非阻塞或挂起),可以立即运行但还没有运行的任务。 正在等待比自己高优先级…...
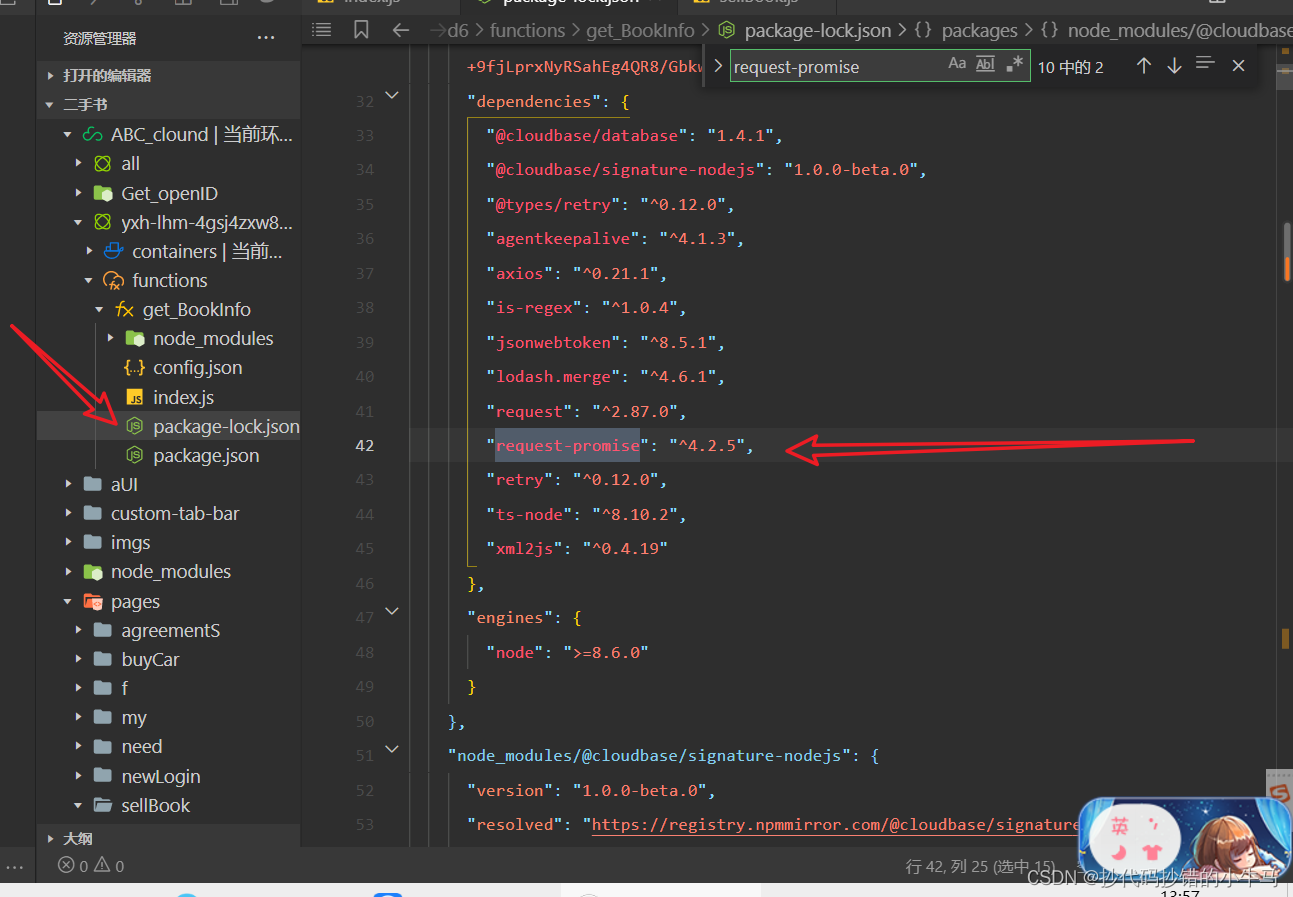
小程序 npm sill idealTree buildDeps 安装一直没反应
目录 一、问题 二、解决 1、删除.npmsrc 、清除缓存 2、更换镜像源 3、最终检测 一、问题 记录:今天npm 一直安装不成功 显示:sill idealTree buildDeps 我的版本: 我百度到换镜像源安装方法,但我尝试后,依然…...
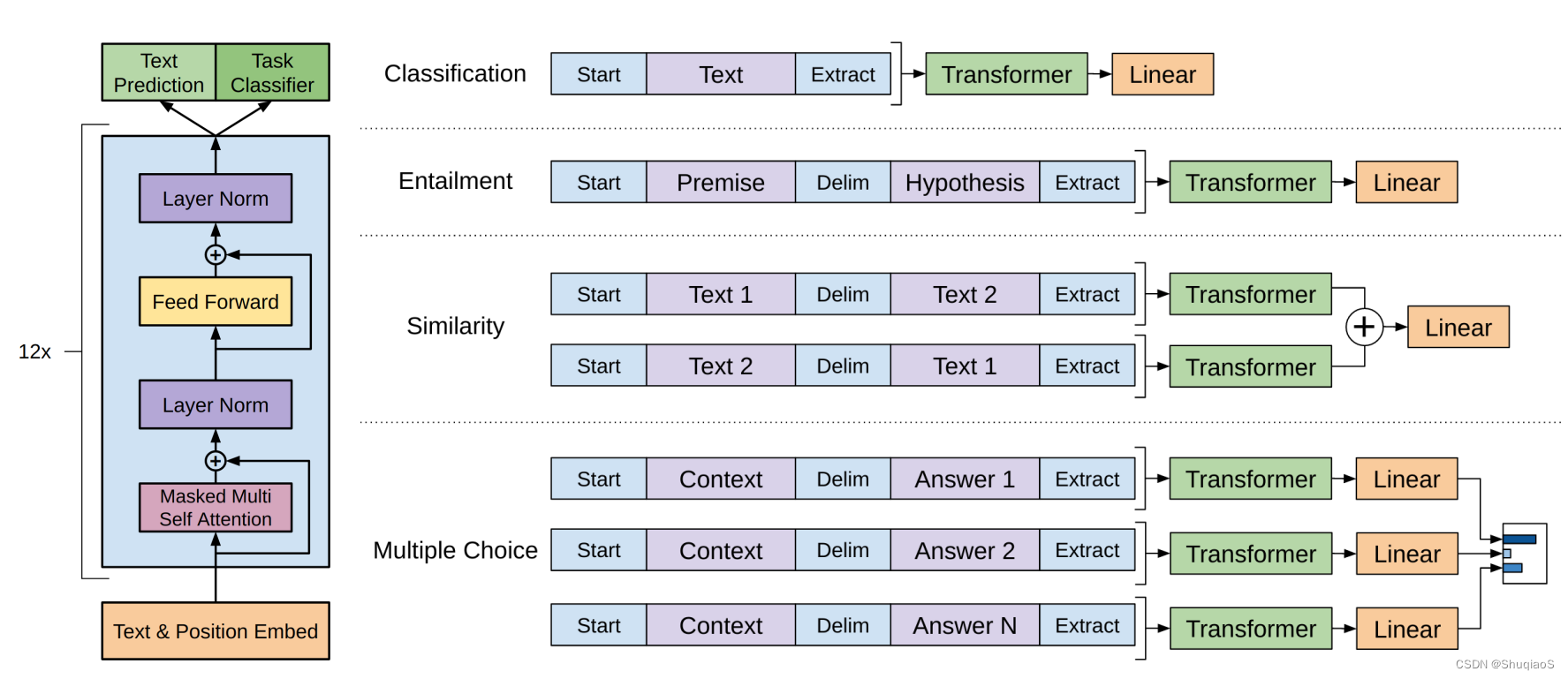
GPT系列详解:初代GPT
本文详细解读了OpenAI公司在2018年6月发布的论文《Improving Language Understanding by Generative Pre-Training》,它其中介绍的算法也就是后来人们说的GPT。本文借鉴了李沐的这个视频,感兴趣的同学可以移步观看大神的讲解。 目录引言GPT方法无监督预训…...

为什么要使用数据库
数据保存在内存优点:存取速度快缺点:数据不能永久保存数据保存在文件优点:数据永久保存缺点:1)速度比内存操作慢,频繁的IO操作。2)查询数据不方便数据保存在数据库1)数据永久保存2&a…...
【单目标优化算法】海鸥优化算法(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
筑基六层 —— 整型提升及实用调式技巧
目录 一.修炼必备 二. 整型提升 三.实用调式技巧 一.修炼必备 1.入门必备:VS2019社区版,下载地址:Visual Studio 较旧的下载 - 2019、2017、2015 和以前的版本 (microsoft.com) 2.趁手武器:印象笔记/有道云笔记 3.修炼秘籍&…...

后端前端文件传输2中传出模式
base64文件传输 app.route(/download, methods[get]) def hello_as(): # 数据 id request.args.get("id") cur g.db.cursor() cur.execute(fselect name,grade,commentNum,cityName,sceneryThemeName from dataList where cityId? , (id,)) …...
【ZOJ 1067】Color Me Less 题解(vector+开方)
问题 颜色缩减是从一组离散颜色到较小颜色的映射。这个问题的解决方案需要在标准的24位RGB颜色空间中执行这样的映射。输入由十六个RGB颜色值的目标集合和要映射到目标集合中最接近的颜色的任意RGB颜色集合组成。为了我们的目的,RGB颜色被定义为有序三元组ÿ…...
凌恩生物经典文章:孟德尔诞辰200周年,Nature Genetics礼献豌豆高质量精细图谱
本期为大家分享的文章是2022年发表在《Nature Genetics》上的一篇文章“Improved pea reference genome and pan-genome highlight genomic features and evolutionary characteristics”,作者通过结合三代pacbio测序、染色体构象捕获(Hi-C)测…...
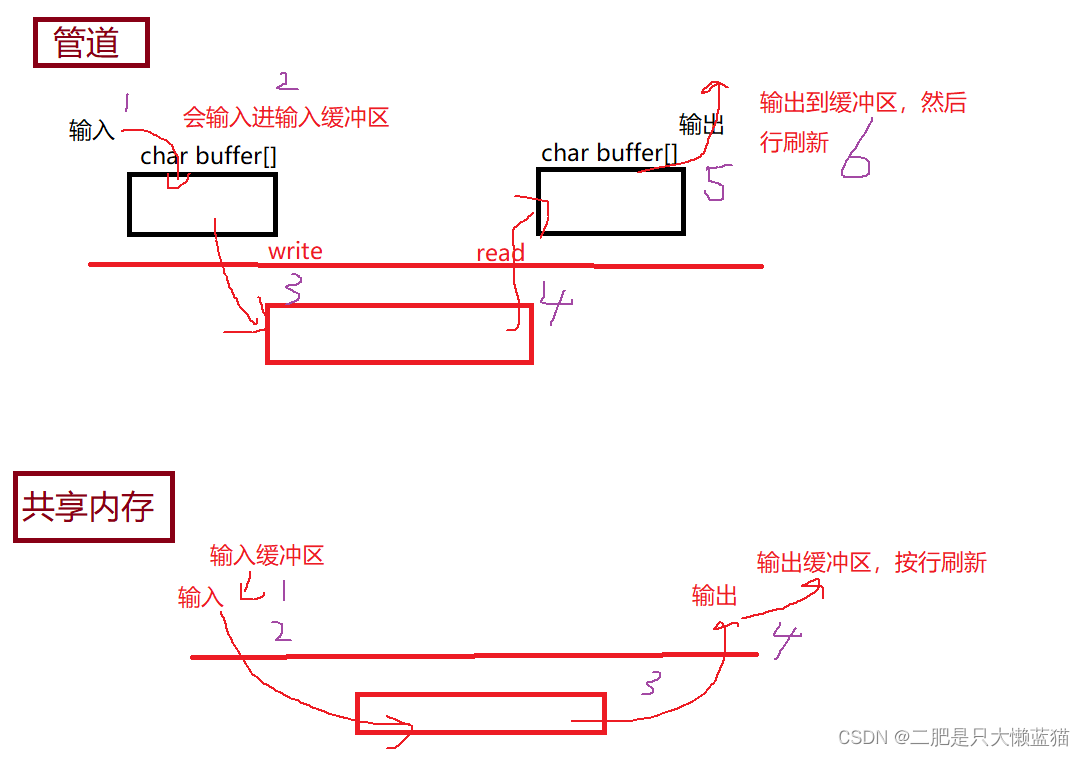
进程间通信(二)/共享内存
⭐前言:在前面的博文中分析了什么的进程间通信和进程间通信的方式之一:管道(匿名管道和命名管道)。接下来分析第二种方式:共享内存。 要实现进程间通信,其前提是让不同进程之间看到同一份资源。所谓共享内存…...

电路模型和电路定律——“电路分析”
各位CSDN的uu们你们好呀,今天小雅兰的内容是我这学期的专业课噢,首先就学习了电路模型和电路定律,包括电路和电路模型、电流和电压的参考方向、电功率和能量、电路元件、电阻元件、电压源和电流源、基尔霍夫定律。那么现在,就让我…...
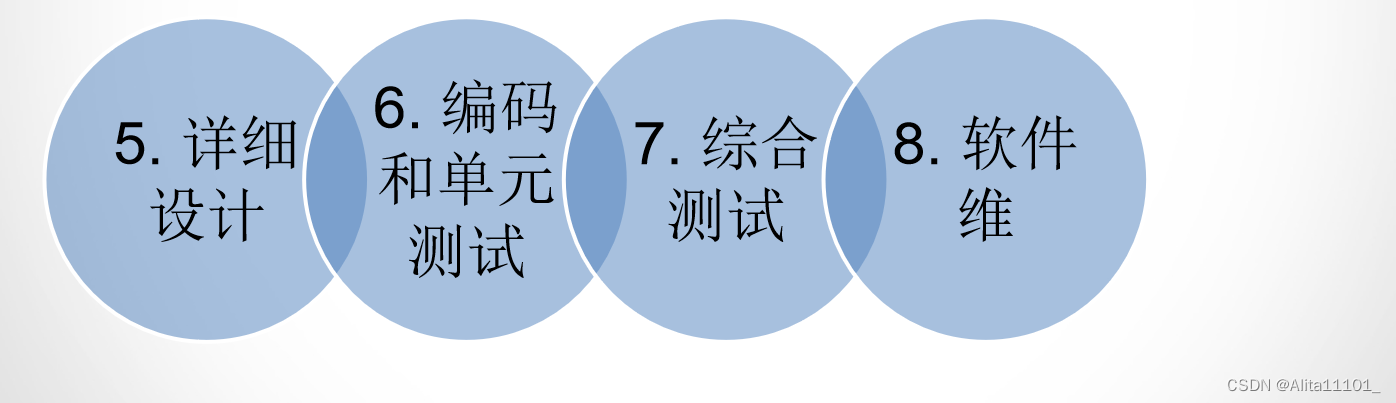
软件工程 | 第一章:软件工程学概述
软件工程学概述一、前言二、软件危机1.典型表现2.产生原因3.消除危机途径三、软件工程1.概述2.软件本质特征3.软件工程基本原理4.软件工程方法学1️⃣传统方法学2️⃣面向对象方法学四、软件生命周期五、结语一、前言 本文将讲述软件工程导论的第一章相关知识点,主…...

前端开发页面HEAD作用
文档类型 为每个 HTML 页面的第一行添加标准模式(standard mode)的声明, 这样能够确保在每个浏览器中拥有一致的表现。 <!DOCTYPE html> 语言属性 为什么使用 lang="zh-cmn-Hans" 而不是我们通常写的 lang="zh-CN" 呢? 请参考知乎上的讨论: …...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...
