GPT系列详解:初代GPT
本文详细解读了OpenAI公司在2018年6月发布的论文《Improving Language Understanding by Generative Pre-Training》,它其中介绍的算法也就是后来人们说的GPT。本文借鉴了李沐的这个视频,感兴趣的同学可以移步观看大神的讲解。
目录
- 引言
- GPT方法
- 无监督预训练
- 有监督微调
- 子任务的描述
- 实验
- 参考文献
引言
在Transformer方法推出的1年后,OpenAI公司发布了GPT系列的第一篇论文,采用生成-判别模型架构,在多个自然语言处理(NLP)任务上实现了较高的精度。
总体而言,GPT方法在很大程度上解决了数据量不足给NLP任务带来的局限;也避免了在不同NLP子任务的解决上,需要不断调整模型的麻烦。
GPT方法
GPT的基本思路是:在有标注的数据集下训练得到一个初始模型,随后在有标注的子任务数据集下,精调得到用于各任务的子模型。在微调时,GPT使用了两个优化的目标函数。
无监督预训练
给定一个语言序列 U={u1,…,un}\mathcal U=\left\{u_1, \dots, u_n\right\}U={u1,…,un},GPT采用标准的语言模型,即最大化如下的目标函数:
L1(U)=∑ilogP(ui∣ui−k,…,ui−1;Θ)L_1(\mathcal U)=\sum_i\text{log}P\left( u_i\vert u_{i-k},\dots,u_{i-1};\Theta\right) L1(U)=i∑logP(ui∣ui−k,…,ui−1;Θ)
其中kkk是上下文窗口的尺寸,条件概率PPP是通过参数为Θ\ThetaΘ的神经网络建模得到的。
简单来说,上面描述的条件概率,是在给定描述模型和位置iii之前的kkk个词后,第iii个位置出现词uiu_iui的概率。将所有概率加起来,就得到了目标函数。这里的窗口尺寸kkk其实可以理解为模型接受的输入序列的长度。当kkk越大时,模型可以消化更多的信息,但是模型也更加复杂。因此,如果希望模型能力很强,这里的kkk可能要取到几十、几百,甚至上千。
注: 目标函数中采用的是所有logPi\text{log} P_ilogPi的和,但是联合概率应该是所有概率的积。这里是相加的原因是,公式中采用了log变换,那么log结果的和也就是所有幂的乘积。不清楚具体变换的同学可以移步这个视频。
具体上,GPT中采用的模型(Θ\ThetaΘ)是Transforer的解码器。Transformer包含两个结构:编码器和解码器。其中,编码器可以看到整个序列中的所有信息;但由于掩码的存在,解码器只能看到非掩码遮盖部分的信息,被遮盖的位置则都是0。由于在语言处理中,模型是只能看到当前词之前的信息的,因此GPT只能采用解码器部分,而不能采用编码器。
更多关于Transformer的介绍,可以移步这篇文章(还在写,挖个坑)详细了解。
有监督微调
精调模型是在有标号的数据集上进行的。具体来说,就是给定一段输入序列和对应的标号,将前面预训练好的模型的最后一层的输出拿出来,经过一个输出层,得到序列最后位置处的估计概率。数学上,这个概率可以表示为:
P(y∣x1,…,xm)=softmax(hlmWy)P\left(y\vert x^1,\dots,x^m\right) = \text{softmax}\left(h_l^mW_y\right) P(y∣x1,…,xm)=softmax(hlmWy)
其中,x1,…,xmx^1,\dots,x^mx1,…,xm是输入,yyy是标签,hlmh_l^mhlm是预训练模型最后一层对位置mmm处的预测结果。
此时,目标函数就是:
L2(C)=∑x,ylogP(y∣x1,…,xm)L_2\left(\mathcal C\right)=\sum_{x,y}\text{log} P\left(y\vert x^1,\dots,x^m\right) L2(C)=x,y∑logP(y∣x1,…,xm)
GPT作者发现,在精调过程中引入预训练的目标函数,同样可以增加模型的精度。因此,微调过程最终的目标函数是两个目标函数的加权求和:
Lc(C)=L2(C)+λ×L1(C)L_c\left(\mathcal C\right)=L_2\left(\mathcal C \right) + \lambda\times L_1\left(\mathcal C\right) Lc(C)=L2(C)+λ×L1(C)
子任务的描述
在知道了目标函数之后,剩下的问题就是如何将NLP中的各种任务,表示成序列对应的标号。在GPT中,这种表示逻辑可以由下图进行表示。
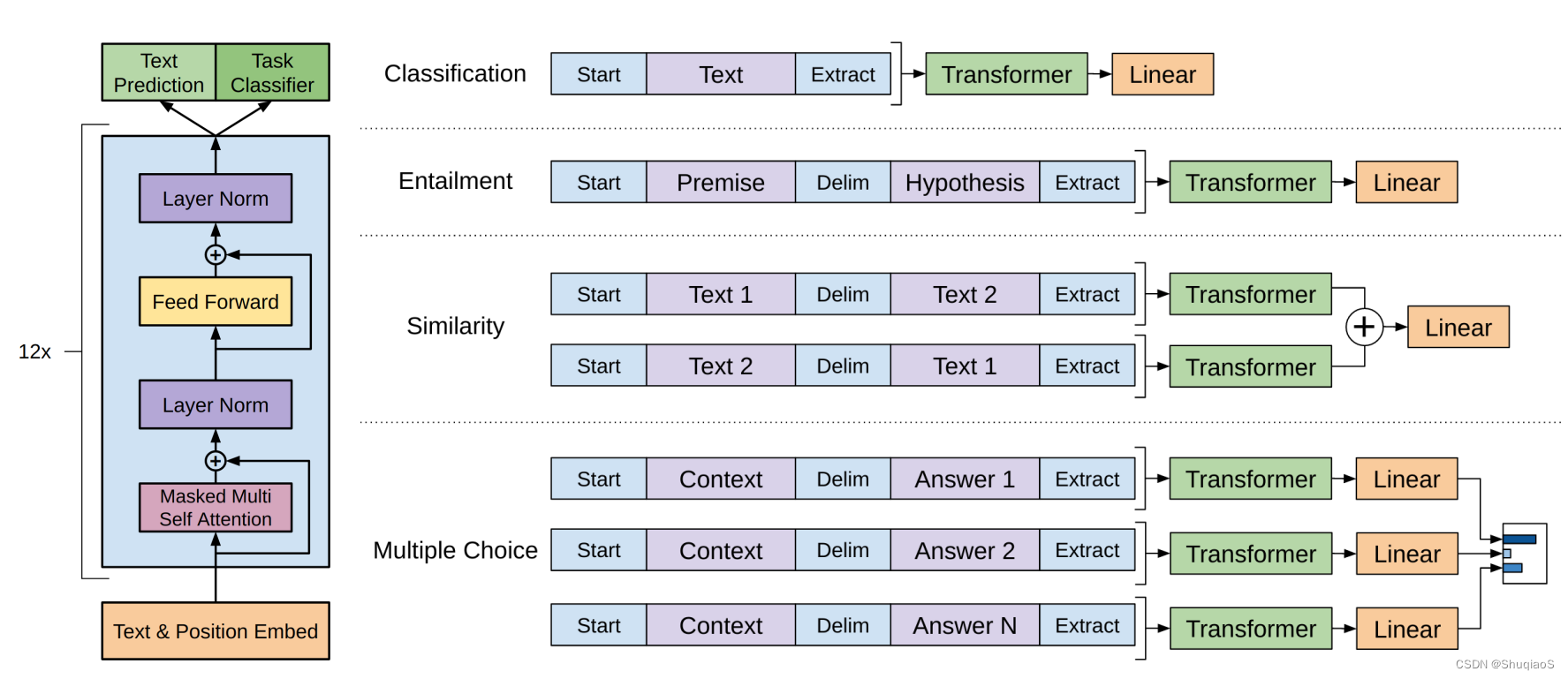
图中给出了4个常见的NLP子任务和其对应的标注方法。从图中可以看出无论是对什么任务,其输入可能被分割成1个、2个甚至多个字段,后面的输出层的结构也可能随任务发生变化,但是其中的transformer部分,一旦训练好了就不需要改变了。这也是GPT与其他NLP方法的一个核心区别。
实验
论文的实验部分本文简要带过,感兴趣的同学请移步论文原文。
这里只提醒大家注意以下几点:
- GPT是在BooksCorpus数据集上训练得到的。这个数据集包含了7000余本未发表的各领域书籍。
- GPT使用了12层的Transformer解码器,每一维是768。
参考文献
- 李沐. GPT,GPT-2,GPT-3 论文精读【论文精读】
- The Math Sorcerer. How to Combine Two Logarithms into a Single Logarithm using Properties of Logs
相关文章:

GPT系列详解:初代GPT
本文详细解读了OpenAI公司在2018年6月发布的论文《Improving Language Understanding by Generative Pre-Training》,它其中介绍的算法也就是后来人们说的GPT。本文借鉴了李沐的这个视频,感兴趣的同学可以移步观看大神的讲解。 目录引言GPT方法无监督预训…...

为什么要使用数据库
数据保存在内存优点:存取速度快缺点:数据不能永久保存数据保存在文件优点:数据永久保存缺点:1)速度比内存操作慢,频繁的IO操作。2)查询数据不方便数据保存在数据库1)数据永久保存2&a…...
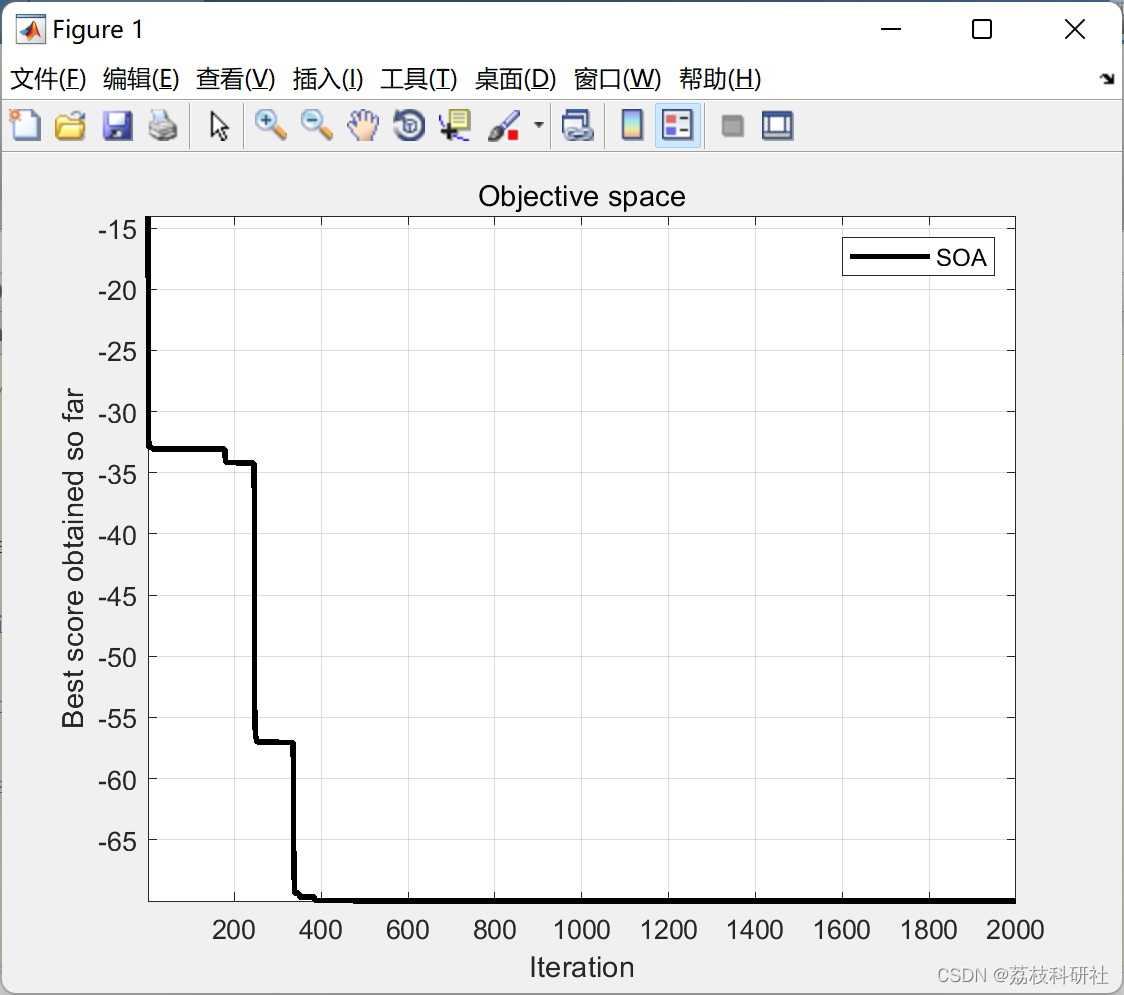
【单目标优化算法】海鸥优化算法(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
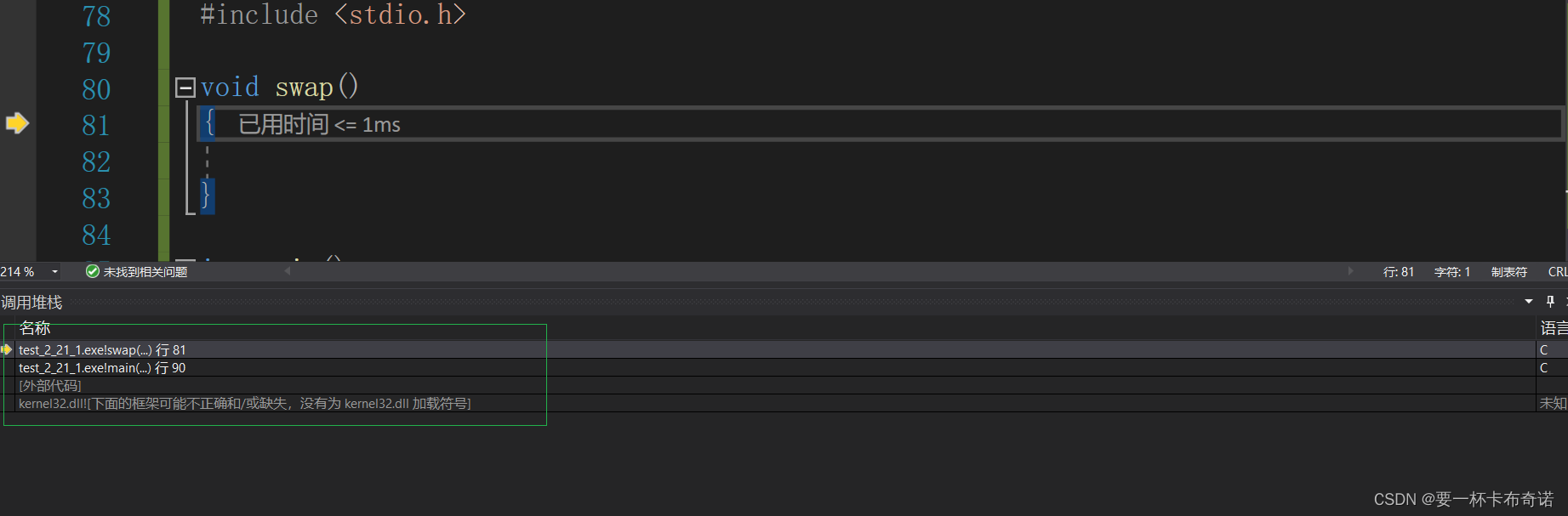
筑基六层 —— 整型提升及实用调式技巧
目录 一.修炼必备 二. 整型提升 三.实用调式技巧 一.修炼必备 1.入门必备:VS2019社区版,下载地址:Visual Studio 较旧的下载 - 2019、2017、2015 和以前的版本 (microsoft.com) 2.趁手武器:印象笔记/有道云笔记 3.修炼秘籍&…...

后端前端文件传输2中传出模式
base64文件传输 app.route(/download, methods[get]) def hello_as(): # 数据 id request.args.get("id") cur g.db.cursor() cur.execute(fselect name,grade,commentNum,cityName,sceneryThemeName from dataList where cityId? , (id,)) …...
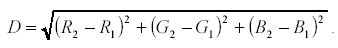
【ZOJ 1067】Color Me Less 题解(vector+开方)
问题 颜色缩减是从一组离散颜色到较小颜色的映射。这个问题的解决方案需要在标准的24位RGB颜色空间中执行这样的映射。输入由十六个RGB颜色值的目标集合和要映射到目标集合中最接近的颜色的任意RGB颜色集合组成。为了我们的目的,RGB颜色被定义为有序三元组ÿ…...
凌恩生物经典文章:孟德尔诞辰200周年,Nature Genetics礼献豌豆高质量精细图谱
本期为大家分享的文章是2022年发表在《Nature Genetics》上的一篇文章“Improved pea reference genome and pan-genome highlight genomic features and evolutionary characteristics”,作者通过结合三代pacbio测序、染色体构象捕获(Hi-C)测…...
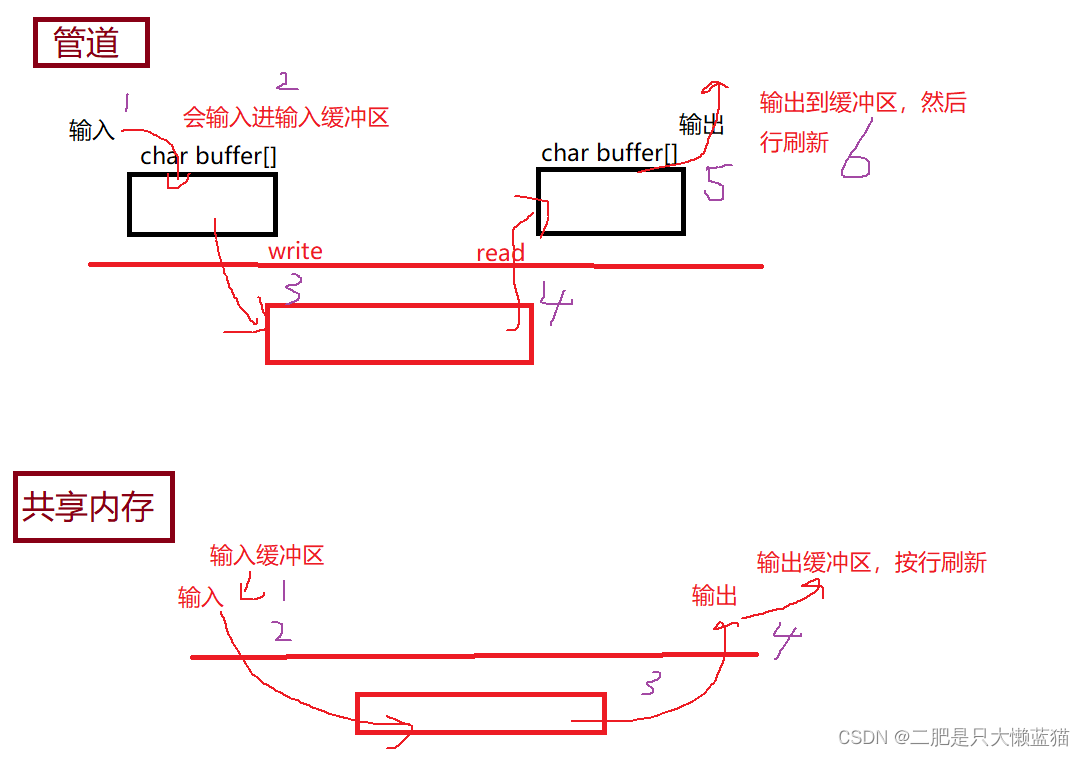
进程间通信(二)/共享内存
⭐前言:在前面的博文中分析了什么的进程间通信和进程间通信的方式之一:管道(匿名管道和命名管道)。接下来分析第二种方式:共享内存。 要实现进程间通信,其前提是让不同进程之间看到同一份资源。所谓共享内存…...

电路模型和电路定律——“电路分析”
各位CSDN的uu们你们好呀,今天小雅兰的内容是我这学期的专业课噢,首先就学习了电路模型和电路定律,包括电路和电路模型、电流和电压的参考方向、电功率和能量、电路元件、电阻元件、电压源和电流源、基尔霍夫定律。那么现在,就让我…...
软件工程 | 第一章:软件工程学概述
软件工程学概述一、前言二、软件危机1.典型表现2.产生原因3.消除危机途径三、软件工程1.概述2.软件本质特征3.软件工程基本原理4.软件工程方法学1️⃣传统方法学2️⃣面向对象方法学四、软件生命周期五、结语一、前言 本文将讲述软件工程导论的第一章相关知识点,主…...

前端开发页面HEAD作用
文档类型 为每个 HTML 页面的第一行添加标准模式(standard mode)的声明, 这样能够确保在每个浏览器中拥有一致的表现。 <!DOCTYPE html> 语言属性 为什么使用 lang="zh-cmn-Hans" 而不是我们通常写的 lang="zh-CN" 呢? 请参考知乎上的讨论: …...

CSS开发技巧——行为技巧
CSS开发技巧——行为技巧 使用overflow-scrolling支持弹性滚动 iOS页面非body元素的滚动操作会非常卡(Android不会出现此情况),通过overflow-scrolling:touch调用Safari原生滚动来支持弹性滚动,增加页面滚动的流畅度 场景:iOS页面滚动 使用t…...
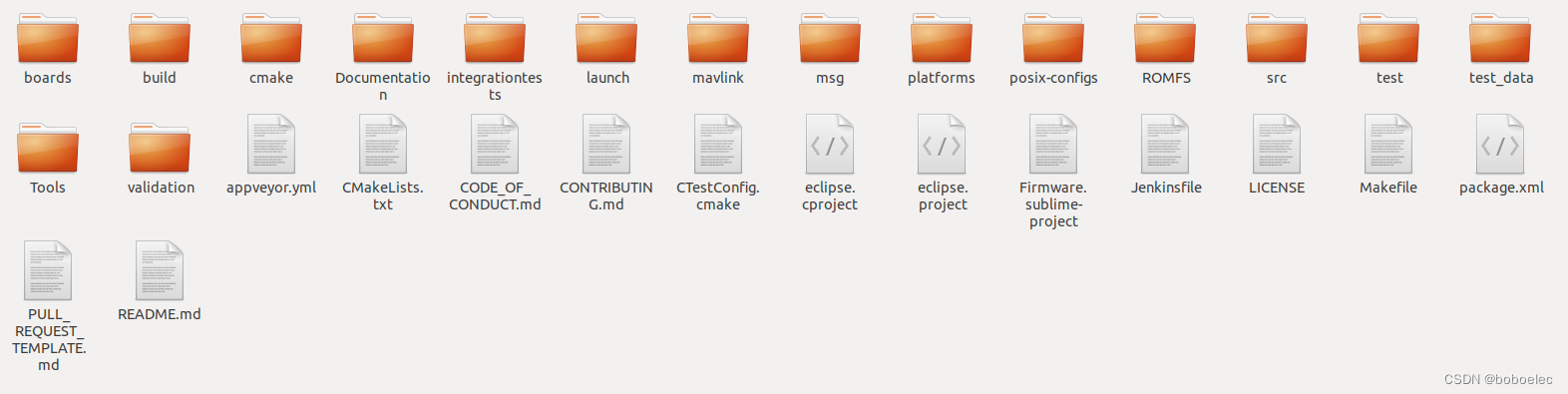
PX4之代码结构
PX4开源飞控是目前主流的开源飞控项目,被很多公司作为飞控开发的参考。也广泛被用于现在流行的evtol验证机的飞控,进行初步的飞行验证。可能大多数AAM以及UAM都离不开PX4。 项目代码可以从github下载 $ git clone --recursive GitHub - PX4/PX4-Autopil…...

【C++11】可变参数模板(函数模板、类模板)
在C11之前,类模板和函数模板只能含有固定数量的模板参数。C11增强了模板功能,允许模板定义中包含0到任意个模板参数,这就是可变参数模板。可变参数模板的加入使得C11的功能变得更加强大,而由此也带来了许多神奇的用法。 可变参数模…...

centos安装高版本cmake
之前centos版本为cmake version 2.8.12.2采用yum remove卸载后重装还是这个版本,看来centos下面就是这个最新了,这说明centos煞笔。于是自己下载cmake包,然后安装。 官方cmake链接地址(3.16)(其他版本自己找,链接给你了) 1,wget下载 2,解压: tar -zxf cmake-3.16.0.…...
重温一下C#的时间类型,并简单写一个定时器功能
🎉🎉 时间是一个非常抽象的概念,本篇文章我们不深究目前电脑上的时候是如何保持全网同步。主要是讲讲在使用C#编程语言里的时间类型。最后使用定时任务简单写一个提醒功能,比如:每天10点准时打开一次csdn首页ÿ…...

MYSQL查询语句执行顺序
SQL语句定义的顺序 (1) SELECT (2)DISTINCT <select_list> (3) FROM <left_table> (4) <join_type> JOIN <right_table> (5) ON <join_condition> (6) WHERE <where_condition> (7) GROUP BY <group_by_list> (8) WITH {C…...

总结:电容在电路35个基本常识
1 电压源正负端接了一个电容,与电路并联,用于整流电路时,具有很好的滤波作用,当电压交变时,由于电容的充电作用,两端的电压不能突变,就保证了电压的平稳。 当用于电池电源时,具有交流…...
Kroger EDI 855 采购订单确认报文详解
本文着重讲述Kroger EDI项目中,供应商发给Kroger的X12 855EDI 规范报文(采购订单确认)解读。 在此前的文章如何读懂X12报文中,我们对X12已经做了详细的介绍,大家可以以此为基础,深入了解855采购订单确认报…...
HANA SDA-远程数据源访问
我们需要把其他系统的数据拿过来,到BW里和财务的数据集成。 HANA SDA就是不复制数据,建立虚拟表(virtual table)来映射到远程数据源。通过这个虚拟表访问其他系统的数据。 对虚拟表的操作现在也可以查询,更新ÿ…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
