【LeetCode题目详解】第九章 动态规划part03 343. 整数拆分 96.不同的二叉搜索树 (day41补)
本文章代码以c++为例!
一、力扣第343题:整数拆分
题目:
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
提示:
2 <= n <= 58
思路
看到这道题目,都会想拆成两个呢,还是三个呢,还是四个....
我们来看一下如何使用动规来解决。
# 动态规划
动规五部曲,分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i]:分拆数字i,可以得到的最大乘积为dp[i]。
dp[i]的定义将贯彻整个解题过程,下面哪一步想不懂了,就想想dp[i]究竟表示的是啥!
- 确定递推公式
可以想 dp[i]最大乘积是怎么得到的呢?
其实可以从1遍历j,然后有两种渠道得到dp[i].
一个是j * (i - j) 直接相乘。
一个是j * dp[i - j],相当于是拆分(i - j),对这个拆分不理解的话,可以回想dp数组的定义。
那有同学问了,j怎么就不拆分呢?
j是从1开始遍历,拆分j的情况,在遍历j的过程中其实都计算过了。那么从1遍历j,比较(i - j) * j和dp[i - j] * j 取最大的。递推公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
也可以这么理解,j * (i - j) 是单纯的把整数拆分为两个数相乘,而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。
如果定义dp[i - j] * dp[j] 也是默认将一个数强制拆成4份以及4份以上了。
所以递推公式:dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
那么在取最大值的时候,为什么还要比较dp[i]呢?
因为在递推公式推导的过程中,每次计算dp[i],取最大的而已。
- dp的初始化
不少同学应该疑惑,dp[0] dp[1]应该初始化多少呢?
有的题解里会给出dp[0] = 1,dp[1] = 1的初始化,但解释比较牵强,主要还是因为这么初始化可以把题目过了。
严格从dp[i]的定义来说,dp[0] dp[1] 就不应该初始化,也就是没有意义的数值。
拆分0和拆分1的最大乘积是多少?
这是无解的。
这里我只初始化dp[2] = 1,从dp[i]的定义来说,拆分数字2,得到的最大乘积是1,这个没有任何异议!
- 确定遍历顺序
确定遍历顺序,先来看看递归公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
dp[i] 是依靠 dp[i - j]的状态,所以遍历i一定是从前向后遍历,先有dp[i - j]再有dp[i]。
所以遍历顺序为:
for (int i = 3; i <= n ; i++) {for (int j = 1; j < i - 1; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}
}
注意 枚举j的时候,是从1开始的。从0开始的话,那么让拆分一个数拆个0,求最大乘积就没有意义了。
j的结束条件是 j < i - 1 ,其实 j < i 也是可以的,不过可以节省一步,例如让j = i - 1,的话,其实在 j = 1的时候,这一步就已经拆出来了,重复计算,所以 j < i - 1
至于 i是从3开始,这样dp[i - j]就是dp[2]正好可以通过我们初始化的数值求出来。
更优化一步,可以这样:
for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}
}
因为拆分一个数n 使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的。
例如 6 拆成 3 * 3, 10 拆成 3 * 3 * 4。 100的话 也是拆成m个近似数组的子数 相乘才是最大的。
只不过我们不知道m究竟是多少而已,但可以明确的是m一定大于等于2,既然m大于等于2,也就是 最差也应该是拆成两个相同的 可能是最大值。
那么 j 遍历,只需要遍历到 n/2 就可以,后面就没有必要遍历了,一定不是最大值。
至于 “拆分一个数n 使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的” 这个我就不去做数学证明了,感兴趣的同学,可以自己证明。
- 举例推导dp数组
举例当n为10 的时候,dp数组里的数值,如下:
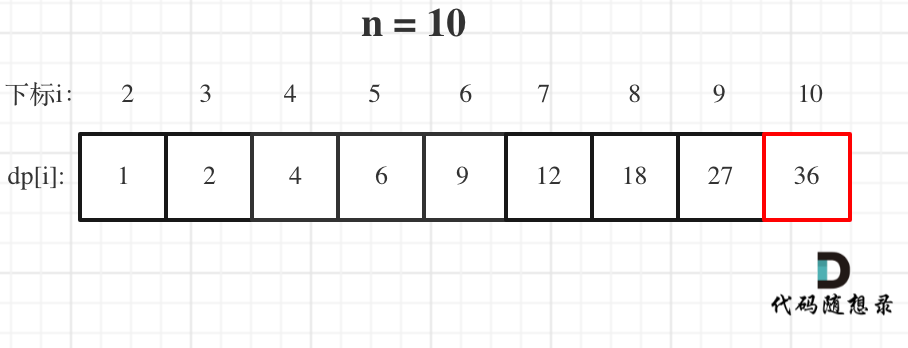
以上动规五部曲分析完毕,C++代码如下:
class Solution {
public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
# 贪心
本题也可以用贪心,每次拆成n个3,如果剩下是4,则保留4,然后相乘,但是这个结论需要数学证明其合理性!
我没有证明,而是直接用了结论。感兴趣的同学可以自己再去研究研究数学证明哈。
给出我的C++代码如下:
class Solution {
public:int integerBreak(int n) {if (n == 2) return 1;if (n == 3) return 2;if (n == 4) return 4;int result = 1;while (n > 4) {result *= 3;n -= 3;}result *= n;return result;}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
# 总结
本题掌握其动规的方法,就可以了,贪心的解法确实简单,但需要有数学证明,如果能自圆其说也是可以的。
其实这道题目的递推公式并不好想,而且初始化的地方也很有讲究,我在写本题的时候一开始写的代码是这样的:
class Solution {
public:int integerBreak(int n) {if (n <= 3) return 1 * (n - 1);vector<int> dp(n + 1, 0);dp[1] = 1;dp[2] = 2;dp[3] = 3;for (int i = 4; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], dp[i - j] * dp[j]);}}return dp[n];}
};
这个代码也是可以过的!
在解释递推公式的时候,也可以解释通,dp[i] 就等于 拆解i - j的最大乘积 * 拆解j的最大乘积。 看起来没毛病!
但是在解释初始化的时候,就发现自相矛盾了,dp[1]为什么一定是1呢?根据dp[i]的定义,dp[2]也不应该是2啊。
但如果递归公式是 dp[i] = max(dp[i], dp[i - j] * dp[j]);,就一定要这么初始化。递推公式没毛病,但初始化解释不通!
虽然代码在初始位置有一个判断if (n <= 3) return 1 * (n - 1);,保证n<=3 结果是正确的,但代码后面又要给dp[1]赋值1 和 dp[2] 赋值 2,这其实就是自相矛盾的代码,违背了dp[i]的定义!
我举这个例子,其实就说做题的严谨性,上面这个代码也可以AC,大体上一看好像也没有毛病,递推公式也说得过去,但是仅仅是恰巧过了而已。
二、力扣第98题:不同的二叉搜索树
题目:
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
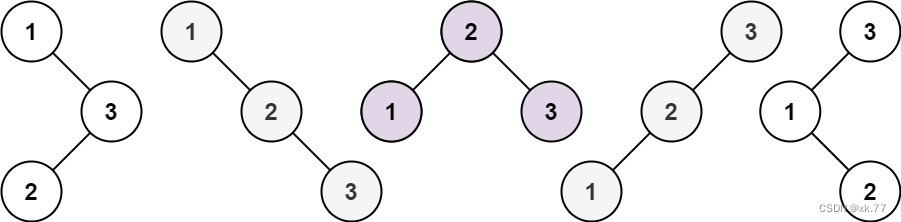
示例 1:
输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 19
思路
这道题目描述很简短,但估计大部分同学看完都是懵懵的状态,这得怎么统计呢?
关于什么是二叉搜索树,我们之前在讲解二叉树专题的时候已经详细讲解过了,也可以看看这篇二叉树:二叉搜索树登场!
(opens new window)再回顾一波。
了解了二叉搜索树之后,我们应该先举几个例子,画画图,看看有没有什么规律,如图:
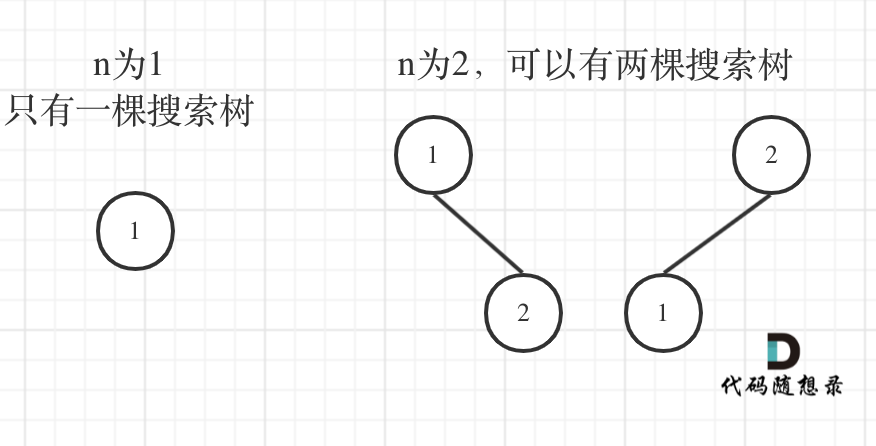
n为1的时候有一棵树,n为2有两棵树,这个是很直观的。
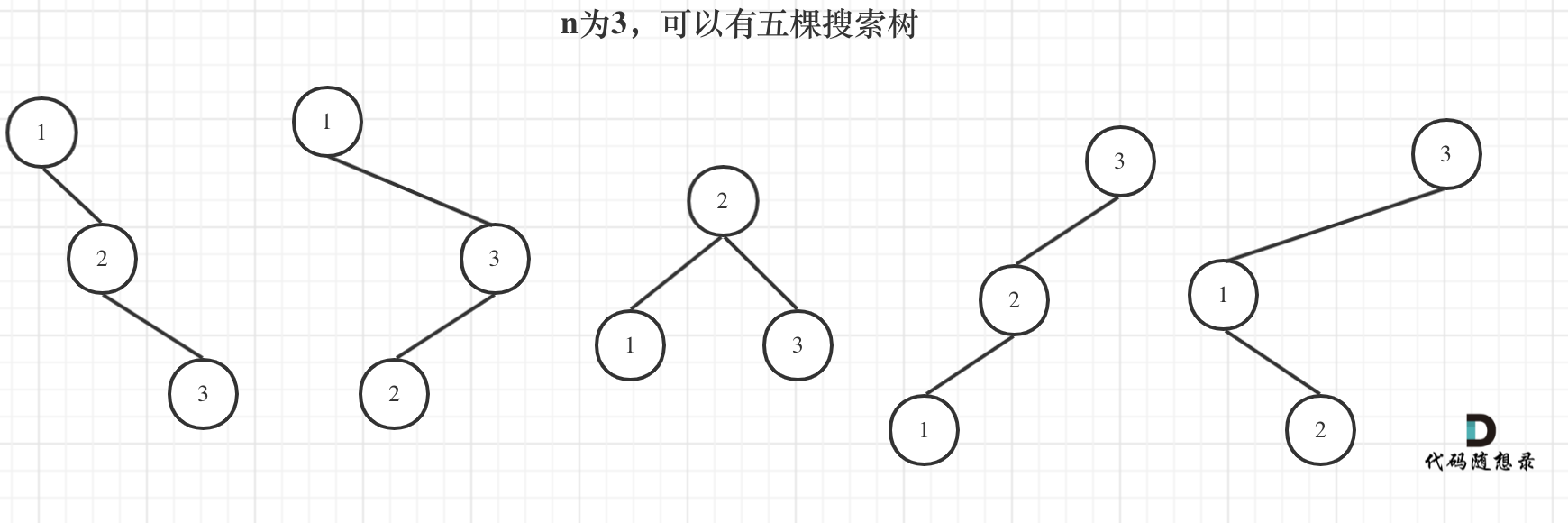
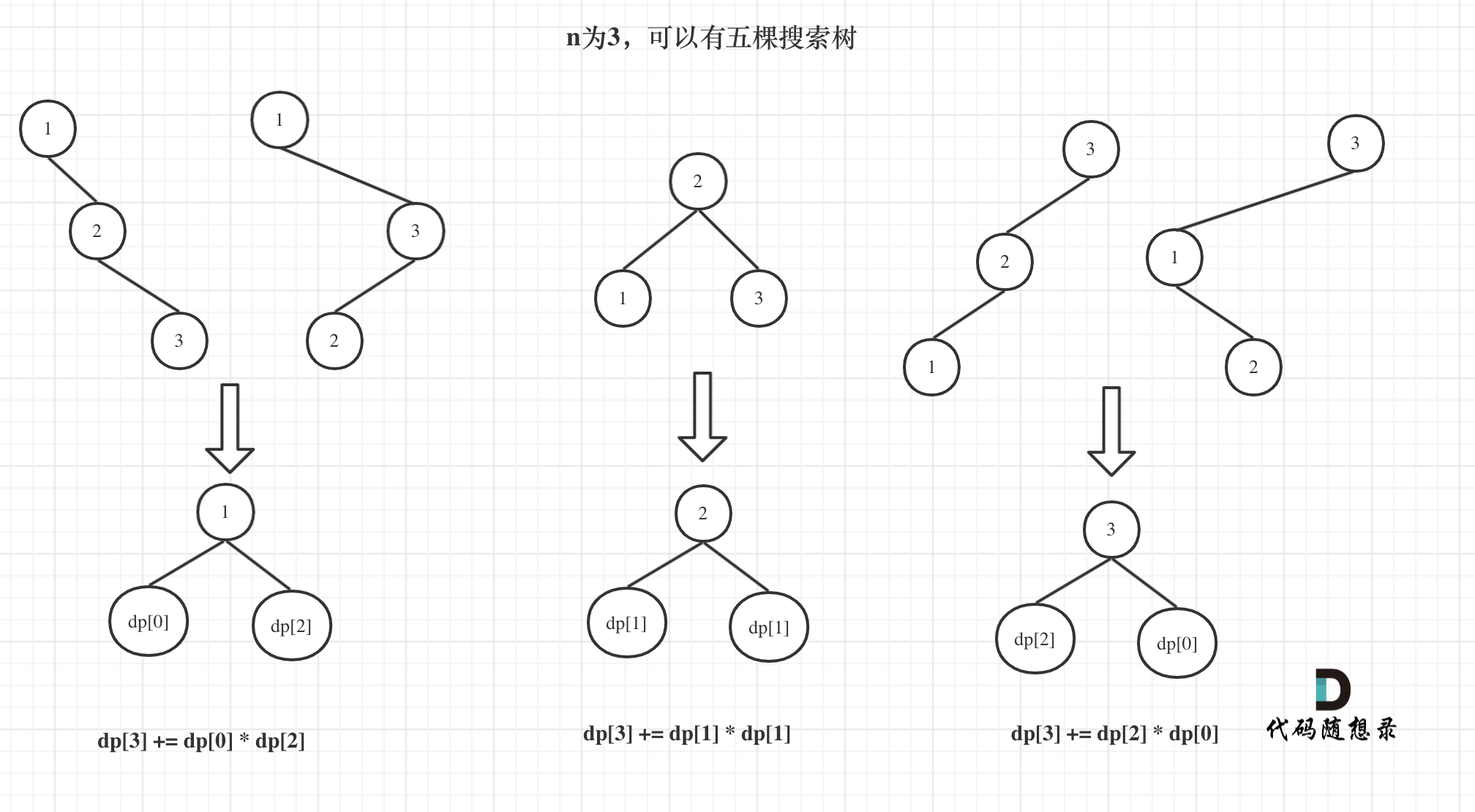
来看看n为3的时候,有哪几种情况。
当1为头结点的时候,其右子树有两个节点,看这两个节点的布局,是不是和 n 为2的时候两棵树的布局是一样的啊!
(可能有同学问了,这布局不一样啊,节点数值都不一样。别忘了我们就是求不同树的数量,并不用把搜索树都列出来,所以不用关心其具体数值的差异)
当3为头结点的时候,其左子树有两个节点,看这两个节点的布局,是不是和n为2的时候两棵树的布局也是一样的啊!
当2为头结点的时候,其左右子树都只有一个节点,布局是不是和n为1的时候只有一棵树的布局也是一样的啊!
发现到这里,其实我们就找到了重叠子问题了,其实也就是发现可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种方式。
思考到这里,这道题目就有眉目了。
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
如图所示:
此时我们已经找到递推关系了,那么可以用动规五部曲再系统分析一遍。
- 确定dp数组(dp table)以及下标的含义
dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]。
也可以理解是i个不同元素节点组成的二叉搜索树的个数为dp[i] ,都是一样的。
以下分析如果想不清楚,就来回想一下dp[i]的定义
- 确定递推公式
在上面的分析中,其实已经看出其递推关系, dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素,从1遍历到i为止。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
- dp数组如何初始化
初始化,只需要初始化dp[0]就可以了,推导的基础,都是dp[0]。
那么dp[0]应该是多少呢?
从定义上来讲,空节点也是一棵二叉树,也是一棵二叉搜索树,这是可以说得通的。
从递归公式上来讲,dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0,也需要dp[以j为头结点左子树节点数量] = 1, 否则乘法的结果就都变成0了。
所以初始化dp[0] = 1
- 确定遍历顺序
首先一定是遍历节点数,从递归公式:dp[i] += dp[j - 1] * dp[i - j]可以看出,节点数为i的状态是依靠 i之前节点数的状态。
那么遍历i里面每一个数作为头结点的状态,用j来遍历。
代码如下:
for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}
}
- 举例推导dp数组
n为5时候的dp数组状态如图:
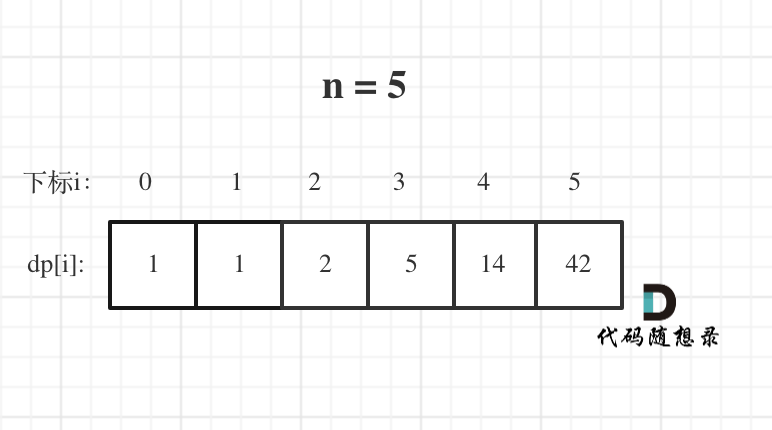
当然如果自己画图举例的话,基本举例到n为3就可以了,n为4的时候,画图已经比较麻烦了。
我这里列到了n为5的情况,是为了方便大家 debug代码的时候,把dp数组打出来,看看哪里有问题。
综上分析完毕,C++代码如下:
class Solution {
public:int numTrees(int n) {vector<int> dp(n + 1);dp[0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];}
};
- 时间复杂度:$O(n^2)$
- 空间复杂度:$O(n)$
大家应该发现了,我们分析了这么多,最后代码却如此简单!
# 总结
这道题目虽然在力扣上标记是中等难度,但可以算是困难了!
首先这道题想到用动规的方法来解决,就不太好想,需要举例,画图,分析,才能找到递推的关系。
然后难点就是确定递推公式了,如果把递推公式想清楚了,遍历顺序和初始化,就是自然而然的事情了。
可以看出我依然还是用动规五部曲来进行分析,会把题目的方方面面都覆盖到!
而且具体这五部分析是我自己平时总结的经验,找不出来第二个的,可能过一阵子 其他题解也会有动规五部曲了,哈哈。
当时我在用动规五部曲讲解斐波那契的时候,一些录友和我反应,感觉讲复杂了。
其实当时我一直强调简单题是用来练习方法论的,并不能因为简单我就代码一甩,简单解释一下就完事了。
可能当时一些同学不理解,现在大家应该感受方法论的重要性了,加油💪
day41补
相关文章:

【LeetCode题目详解】第九章 动态规划part03 343. 整数拆分 96.不同的二叉搜索树 (day41补)
本文章代码以c为例! 一、力扣第343题:整数拆分 题目: 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输…...

半导体制造常用软件工具总结
半导体制造常用软件工具总结 CIM:Computer Integrated Manufacturing 设备自动化,总称MES:Manufacturing Execution System 制造执行系统EAP:Equipment Automation Programming 设备自动化,是MES与设备的桥梁APC&…...
基于Python的IOS自动化测试环境搭建
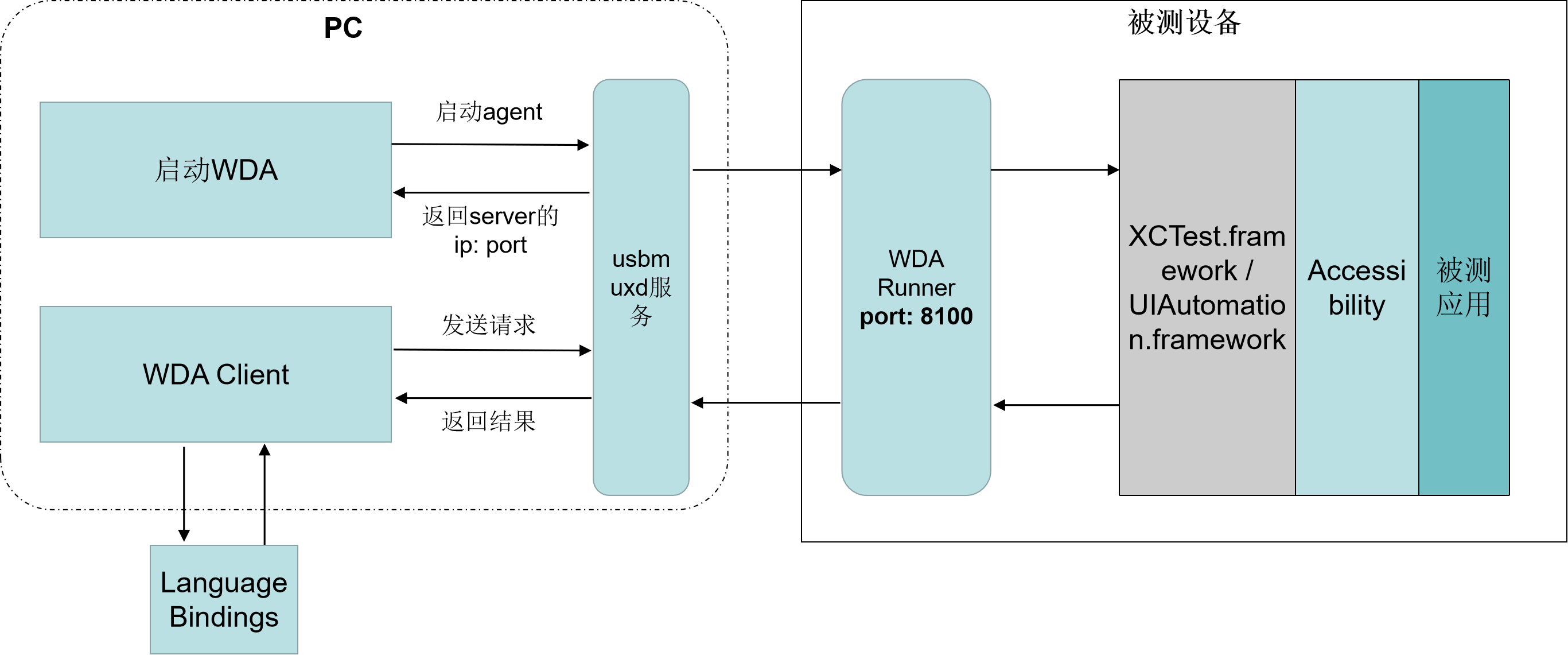
文章目录 一、测试架构介绍1.1 WebDriverAgent原理分析1.2 tidevice原理分析二、环境安装2.1 iOS 设备安装 WebDriverAgent2.2 安装iTunes2.3 安装tidevice2.4 安装facebook-wda自动化三、操作流程四、Weditor的安装和使用一、测试架构介绍 以下为测试架构原理图 手机端的WDA…...

技术领导力实战笔记25
25|用心做好“鼓励式”管理 激发正能量 授权 分工作: 老人干新事,新人干老事,强者干难事,弱者干细事 新人干老事 所谓新人,是对业务产品不了解,对工作流程不清晰的岗位新人。对于新人来说&…...

设计模式-职责链+反射
文章目录 前言简单版本的职责链加反射职责链反射思路过程总结 前言 最近学习设计模式对于职责链的学习有了一些深入的了解故此有了这篇博客 简单版本的职责链加反射 职责链模式(Chain of Responsibility Pattern)和反射(Reflection&#x…...
Middleware ❀ Kafka功能与使用详解
文章目录 1. 概述1.1. 消息队列1.2. 应用场景1.3. 工作模式1.4. 基础结构1.4.1. 结构组件1.4.2. 数据同步1.4.3. ACK机制1.4.4. 分区机制1.4.4.1. 使用Partition Key写入1.4.4.2. 轮询写入 - 默认规则1.4.4.3. 指定Partition写入 1.4.5. Offset偏移量1.4.5.1. 消息顺序性1.4.5.…...
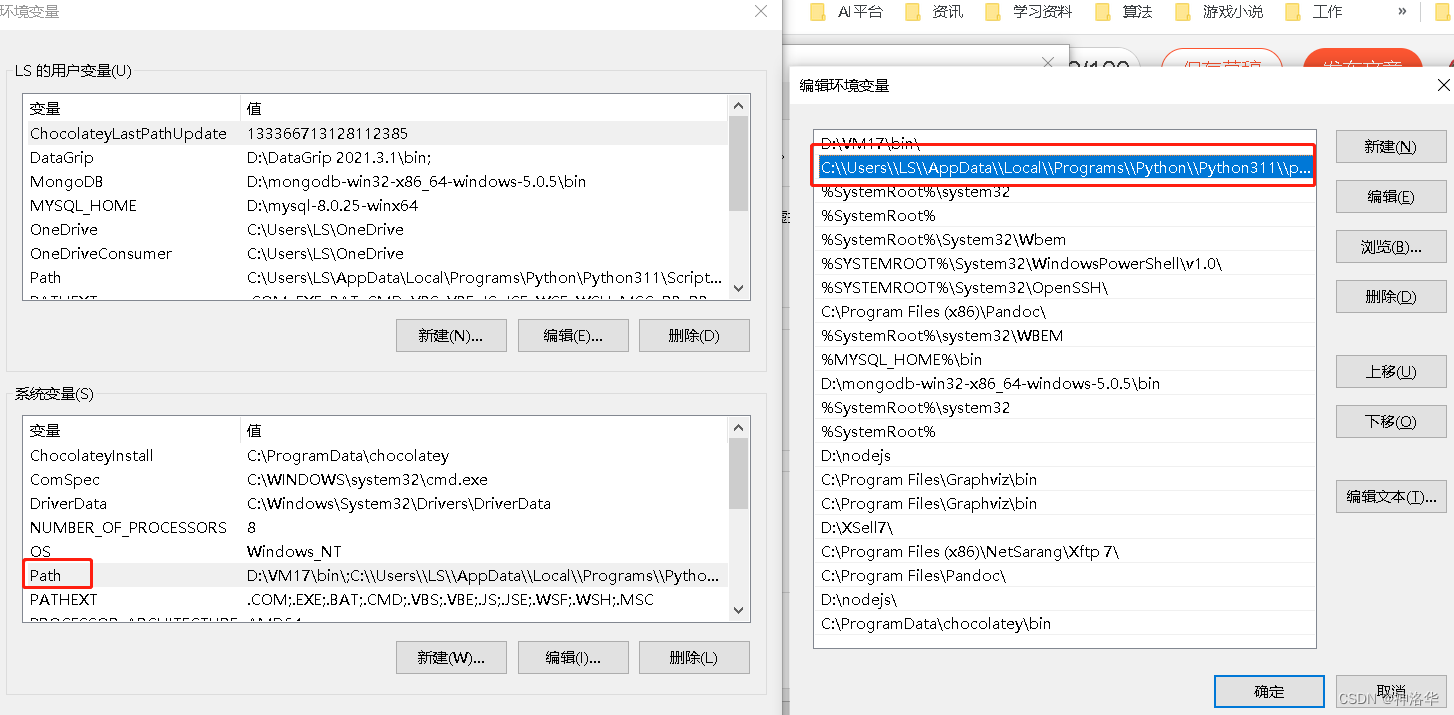
python3.11教程1:python基础语法、程序控制、函数
文章目录 一、Python简介1.1 为什么学习python1.2 python安装与配置1.3 python解释器1.4 命令行参数1.4.1 sys.argv变量1.4.2 -c和-m选项 1.5 解释器的运行环境1.5.1 编码格式1.5.2 编码声明 二、Python基础语法2.1 行结构2.2 变量(标识符)2.3 字节串2.4…...

【C++】关于using namepace xxx 使用命名空间和冲突
官方定义 namespace是指 标识符的各种可见范围。命名空间用关键字namespace来定义。 命名空间是C的一种机制,用来把单个标识符下的大量有逻辑联系的程序实体组合到一起。此标识符作为此组群的名字。 基本使用 编译及执行命令: g test.cpp -o test ./…...

Linux常用命令——cupsenable命令
在线Linux命令查询工具 cupsenable 启动指定的打印机 补充说明 cupsenable命令用于启动指定的打印机。 语法 cupsenable(选项)(参数)选项 -E:当连接到服务器时强制使用加密; -U:指定连接服务器时使用的用户名; -uÿ…...

基于Stable Diffusion的AIGC服饰穿搭实践
本文主要介绍了基于Stable Diffusion技术的虚拟穿搭试衣的研究探索工作。文章展示了使用LoRA、ControlNet、Inpainting、SAM等工具的方法和处理流程,并陈述了部分目前的实践结果。通过阅读这篇文章,读者可以了解到如何运用Stable Diffusion进行实际操作&…...

【 ARMv9 Cluster BUS QoS 配置】
文章目录 ARM Cluster QoS ARM Cluster QoS QoS(Quality of Service,服务质量)在 ARM 架构中,主要指的是一种机制,它可以控制和管理系统资源(如内存、总线带宽等)的使用,以满足各种…...
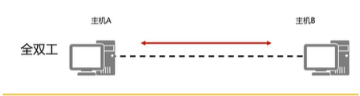
简单了解网络基本概念
目录 一、网络含义 二、什么是以太网? 三、网络分类 四、网络架构 五、数据传输方式 六、双工模式 一、网络含义 在实际生活中我们用传输介质把独立的终端设备相互连接起来就构成了网络。 二、什么是以太网? 以太网是一种网络通信协议标准&#…...

网络安全知识库
0x00 前言 本篇用来整理所有的零散的知识,作为一个技能树或者技能表来进行引导 CTF 加解密合集CTF Web合集 0x01 Http 1.http头 1.1 本地访问识别 如何伪造http头,让后端认为是本地访问...

无涯教程-JavaScript - FLOOR函数
描述 FLOOR函数将数字向下舍入为零,直到最接近的有效倍数。 语法 FLOOR (number, significance)争论 Argument描述Required/OptionalNumberThe numeric value you want to round.RequiredSignificanceThe multiple to which you want to round.Required Notes 如果数字的符…...
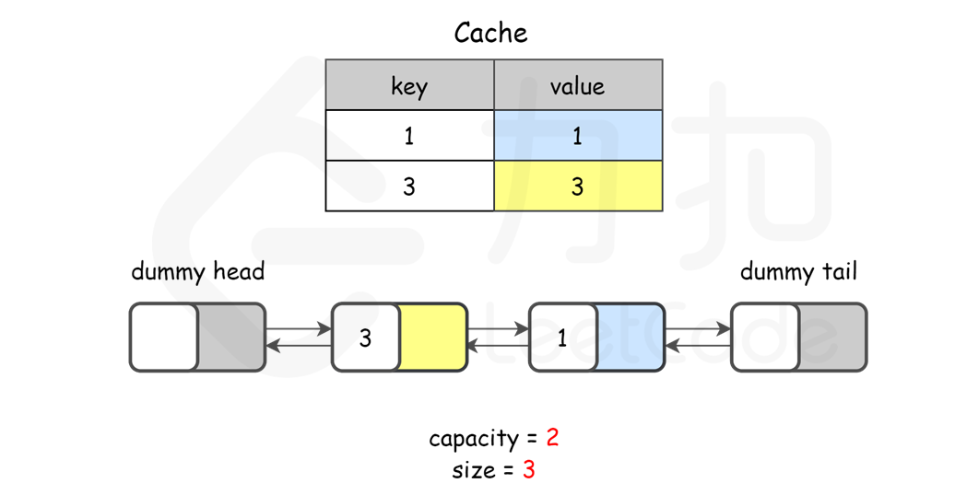
【LeetCode-中等题】146. LRU 缓存
文章目录 题目方法一:直接继承LinkedHashMap调用api方法二:自定义LinkedHashMap HashMap ListNode LinkedHashMap 题目 LRU缓存是什么:LRU缓存机制,你想知道的这里都有 实现 LRU 缓存算法 方法一:直接继承Linked…...

表白墙程序
目录 一、页面代码部分 二、设计程序 二、实现 doPost编辑 三、实现 doGet 四、前端代码部分 五、使用数据库存储数据 一、页面代码部分 在之前的一篇博客中,已经写过了表白墙的页面代码实现,这里就不再重复了 页面代码如下: <!…...

git 本地仓库关联到远程仓库
将本地仓库关联到远程仓库 方式一:远程仓库没有文件 第一步: git init(初始化git仓库) 第二步: git remote add 地址(设置remote地址) 第三步: git add . (将所有变…...

Introducing Language Guidance in Prompt-based Continual Learning
本文是LLM系列文章,针对《Introducing Language Guidance in Prompt-based Continual Learning》的翻译。 基于提示的持续学习中引入语言指导 摘要1 引言2 相关工作3 背景4 基于提示的持续学习语言指导5 实验6 结论 摘要 持续学习旨在学习一系列任务的单一模型&am…...
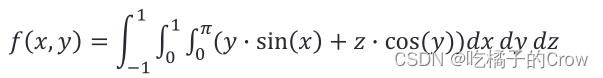
Matlab(数值微积分)
目录 1.多项式微分与积分 1.1 微分 1.2 多项式微分 1.3 如何正确的使用Matlab? 1.3.1 Matlab表达多项式 1.3.2 polyval() 多项式求值 1.3.3 polyder()多项式微分 1.4 多项式积分 1.4.1 如何正确表达 1.4.2 polyint() 多项式积分 2.数值的微分与积分 2.1 数值微分 2…...
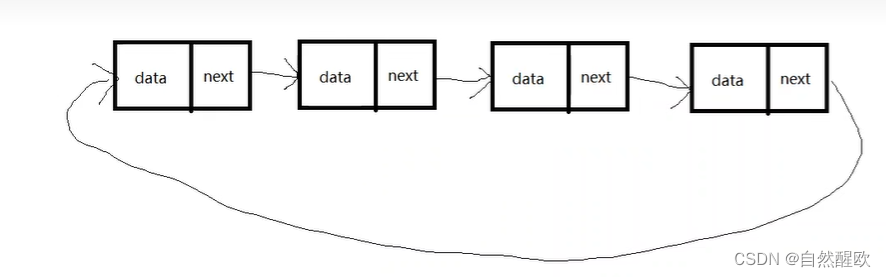
【数据结构回顾】
数据结构回顾 一、单链表二、单循环链表 一、单链表 #include <stdio.h> #include <stdlib.h>typedef struct Node {int data;Node *next; }Node;Node* initList() {Node *list (Node*)malloc(sizeof(Node));list->data 0;list->next NULL;return list; }…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...

NineData数据库DevOps功能全面支持百度智能云向量数据库 VectorDB,助力企业 AI 应用高效落地
NineData 的数据库 DevOps 解决方案已完成对百度智能云向量数据库 VectorDB 的全链路适配,成为国内首批提供 VectorDB 原生操作能力的服务商。此次合作聚焦 AI 开发核心场景,通过标准化 SQL 工作台与细粒度权限管控两大能力,助力企业安全高效…...
