线性代数的学习和整理17:向量空间的基,自然基,基变换等(未完成)
目录
3 向量空间的基:矩阵的基础/轴
3.1 从颜色RGB说起
3.2 附属知识
3.3 什么样的向量可以做基?
3.4 基的分类
3.1.1 不同空间的基---向量组的数量可能不同
3.1.2 自然基
3.1.3 正交基
3.1.4 标准正交基
3.1.5 基和向量/矩阵
3.1.6 基变换
(1)基不变,坐标变换
(2)坐标不变,基变换
3.1.6 基变换和坐标变换的公式 (待完成)
基的英语
3 向量空间的基:矩阵的基础/轴
3.1 从颜色RGB说起
- RGB颜色大家都明白原理
- 实际上就是 red, green,blue 这3元色来生成其他颜色
- RGB颜色有2种数字化 表示方式
- 比如 ffffff 000000 ,这个是16进制数字来表示颜色
- 使用RGB的向量值来表示其他颜色的,比如 黑色是(0,0,0) ,白色是(255,255,255), 而后面这种方法,就是向量和矩阵的方法
- 实际上 RGB 是三原色,也就是 颜色空间/ 可以看成一个3维空间的基
- 其中 red 是
green 是
,blue是
- 任意一种颜色都可以写成
3.2 附属知识
1 十六进制
(常用数字0、1、2、3、4、5、6、7、8、9和字母A、B、C、D、E、F(a、b、c、d、e、f)表示,其中:A~F表示10~15,这些称作十六进制数字。)
2 颜色的RGB值
- RGB值从0-255,实际这个数字代表亮度
- 总共有256*256*256种,
| 颜色名称 | 红色值 Red | 绿色值 Green | 蓝色值 Blue | ||||
| 黑色 | 0 | 0 | 0 | ||||
| 蓝色 | 0 | 0 | 255 | ||||
| 绿色 | 0 | 255 | 0 | ||||
| 青色 | 0 | 255 | 255 | ||||
| 红色 | 255 | 0 | 0 | ||||
| 亮紫色(洋红色) | 255 | 0 | 255 | ||||
| 黄色 | 255 | 255 | 0 | ||||
| 白色 | 255 | 255 | 255 | ||||

3.3 什么样的向量可以做基?
向量空间的基的严格定义:向量空间中的某组向量 A= {a1,a2.....an} ,这些向量如果是这个向量空间的最大线性无关组,那么这组向量A就是这个空间的一组基。
总结可以做基的特征
A= {a1,a2.....an} 这组向量,或这个向量组
- 必须是线性无关的。
- 而且必须是这个空间的最大线性无关组。
理论上,颜色空间的基有无数组,但是很多向量组也不能作为基本
举例
- 比如RG这2种颜色构成的向量组,不能称为RGB空间的一组基,因为RG组成不了所有颜色
- 比如线性相关的3组向量: 深绿色(0,255,0),标准绿色(0,100,0) 和蓝色(0,0,255)不能作为颜色空间的基的,因为3个线性相关的颜色基,无法组成所有颜色。
3.4 基的分类
3.1.1 不同空间的基---向量组的数量可能不同
- (a1,a2)是2维的,对应2个基底e1,e2
- (a1,a2,a3)是3维的,对应3个基底e1,e2
- (a1,a2,a3... ... an)是n维的, 对应n个基底e1,e2.....en
3.1.2 自然基
- 自然基本特指这种
- 自然基,比然是正交基,也是标准正交基
3.1.3 正交基
- 基这组向量里的每个向量都是互相 垂直/正交的
3.1.4 标准正交基
- 基这组向量里的每个向量都是互相 垂直/正交的
- 且长度都为1
- 标准正交基有很多,并不只是只有自然基那一组!
3.1.5 基和向量/矩阵
- 比如一个向量(3,2,5) 就可以认为是,这个向量的3个元素分别在3个基上的长度/伸缩度
- 向量(3,2,5) 在第1个基,(1,0,0) 上的长度/伸缩度是3,
- 向量(3,2,5) 在第2个基,(0,1,0) 上的长度/伸缩度是2,
- 向量(3,2,5) 在第3个基,(0,0,1) 上的长度/伸缩度是5,
3.1.6 基变换
- 矩阵的 基 / 基底 是可以改变的
- 实际上Ax=y 就可以看作 基变换
- Ax=y 有两种方法,要么坐标变,要么坐标不变,基变化

(1)基不变,坐标变换
- 假设我们有A是e1,e2,e3 等 自然基下的向量x
- 计算 A*x=y
- 一般我们计算 A*x=y 其实都是将 向量x 经过矩阵A变换后,生成了新的向量y,而新的向量y实际就是原向量的坐标发生了变化,其仍然是e1,e2。。。等 自然基下的向量y
(2)坐标不变,基变换
- 假设我们有A是e1,e2。。。等自然基下的向量x
- 而A的列向量分别是 α1,α2 ....
- 计算 A*x=y
- 我们可以保持x向量的坐标还是老的,但是基不再用e1,e2。。。等,而是用A的列向量α1,α2 ....作为新的基.
3.1.6 基变换和坐标变换的公式 (待完成)

相关文章:

线性代数的学习和整理17:向量空间的基,自然基,基变换等(未完成)
目录 3 向量空间的基:矩阵的基础/轴 3.1 从颜色RGB说起 3.2 附属知识 3.3 什么样的向量可以做基? 3.4 基的分类 3.1.1 不同空间的基---向量组的数量可能不同 3.1.2 自然基 3.1.3 正交基 3.1.4 标准正交基 3.1.5 基和向量/矩阵 3.1.6 基变换 …...

Java中支持分库分表的框架/组件/中间件简介
文章目录 1 sharding-jdbc2 TSharding3 Atlas4 Cobar5 MyCAT6 TDDL7 Vitess 列举一些比较常见的,简单介绍一下: sharding-jdbc(当当) TSharding(蘑菇街) Atlas(奇虎360) Cobar&#…...
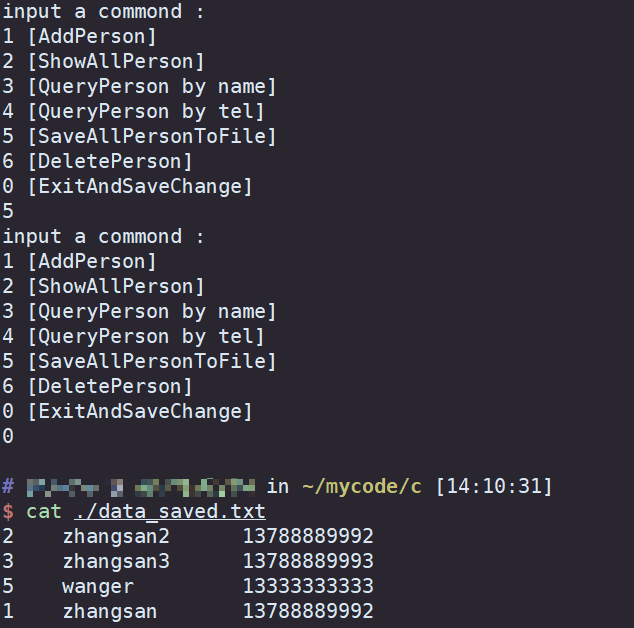
7.2 项目2 学生通讯录管理:文本文件增删改查(C 版本)(自顶向下设计+断点调试) (A)
C自学精简教程 目录(必读) 该作业是 作业 学生通讯录管理:文本文件增删改查(C版本) 的C 语言版本。 具体的作业题目描述,要求,可以参考 学生通讯录管理:文本文件增删改查(C版本)。…...
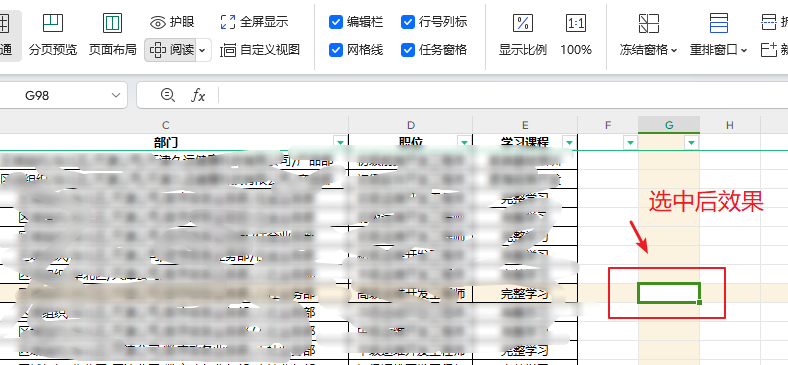
excel怎么设置任意选一个单元格纵横竖横都有颜色
有时excel表格内容过多的时候,我们通过excel设置任意选一个单元格纵横,竖横背景颜色,这样会更加具有辨识度。设置方式截图如下 设置成功后,预览的效果图...

期货-股票交易规则
交易时间 港股:9:00~9:20 集合竞价,9:3012:00,13:0016:00 持续交易,16:00~16:10 随机收市竞价沪股:9:00~9:25 集合竞价,9:3011:30,13:0015:00 持续交易,11:30~12:00 交易申报深股&a…...

Makefile一些语法
ifneq($(filter true,$(xxx)), )的含义 filter 是过滤的意思,它的原型是:$(filter PATTERN…,TEXT), 意义为:过滤掉字串“TEXT”中所有不符合模式“PATTERN”的单词,保留所有符合此模式的单词做返回值。 结合前面的if…...

0基础可以转行编程行业么
在2022年分行业门类分岗位就业人员年平均工资中,信息传输、软件和信息技术服务业的薪资遥遥领先其他行业,为全国平均薪资水平的 1.78 倍,远超第二名金融行业,其年增长率在9.4%,并成为年收入首个过20 万门槛的行业&…...

【spark】dataframe慎用limit
官方:limit通常和order by一起使用,保证结果是确定的 limit 会有两个步骤: LocalLimit ,发生在每个partitionGlobalLimit,发生shuffle,聚合到一个parttion 当提取的n大时,第二步是比较耗时的…...

基于OpenCV+LPR模型端对端智能车牌识别——深度学习和目标检测算法应用(含Python+Andriod全部工程源码)+CCPD数据集
目录 前言总体设计系统整体结构图系统流程图 运行环境Python 环境OpenCV环境Android环境1. 开发软件和开发包2. JDK设置3. NDK设置 模块实现1. 数据预处理2. 模型训练1)训练级联分类器2)训练无分割车牌字符识别模型 3. APP构建1)导入OpenCV库…...

C++学习6
C学习6 基础知识std::thread 实战boost domain socket server 基础知识 std::thread std::thread是C11标准库中的一个类,用于创建并发执行的线程。它的详细用法如下: 头文件 #include <thread>创建线程 std::thread t(func, args...);其中&am…...

bazel使用中存在的问题
只开远端缓存时。kernel采用的bazel编译,遇到如下问题: 1、Action 详情二进制文件解析为文本文件时报错,无法进一步比较分析导致缓存不命中的原因。--- JDK版本的问题 2、远端缓存全部命中时间收益不明显 ---需分析是否为网络原因 3、$HOM…...
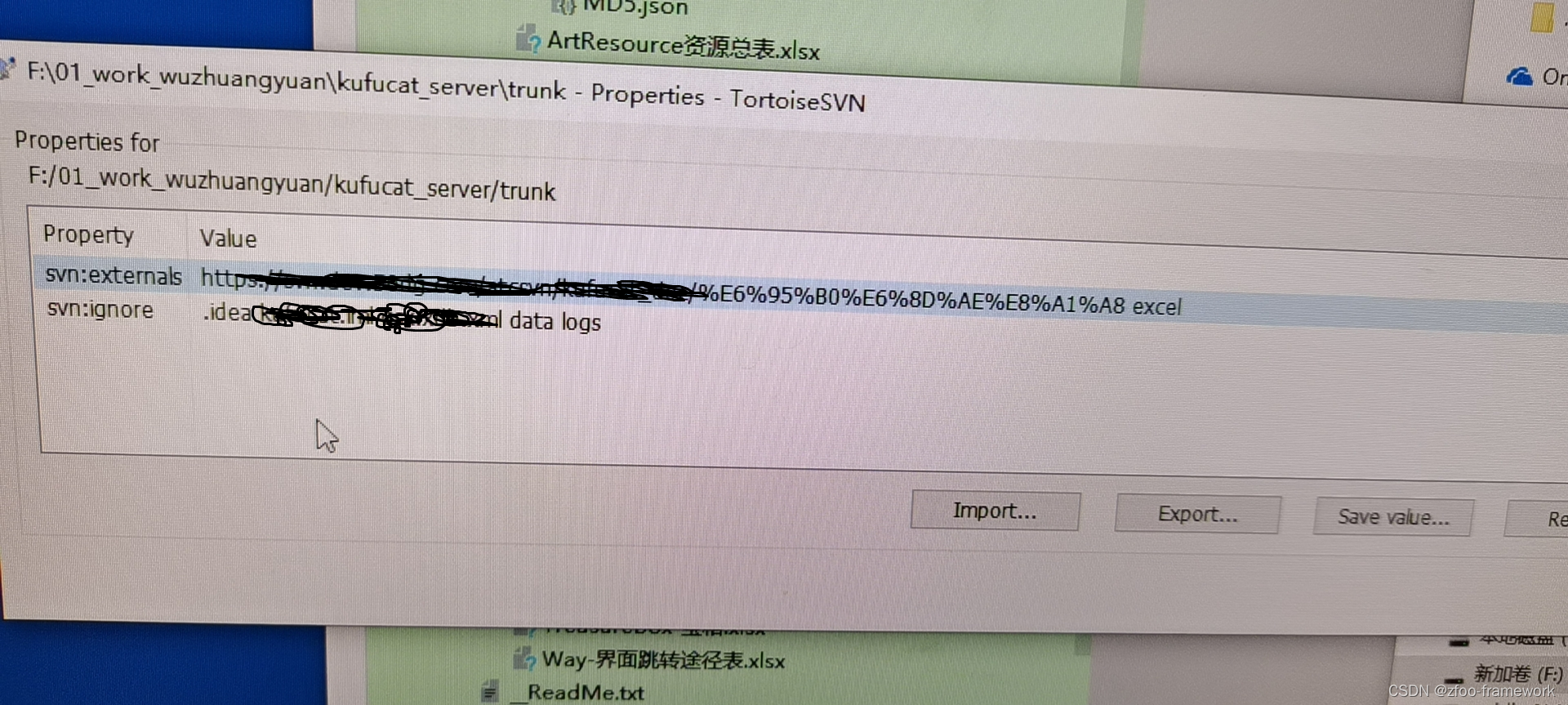
svn软连接和文件忽略
软连接 1)TortoiseSVN->Properties->New->Externals->New 2)填入软连接信息 Local path: 写下软连接后的文件夹的名字 URL: 想要软连接的牡蛎->TortoiseSVN->Repo-browser 复制下填入 文件忽略 以空格隔开就行...
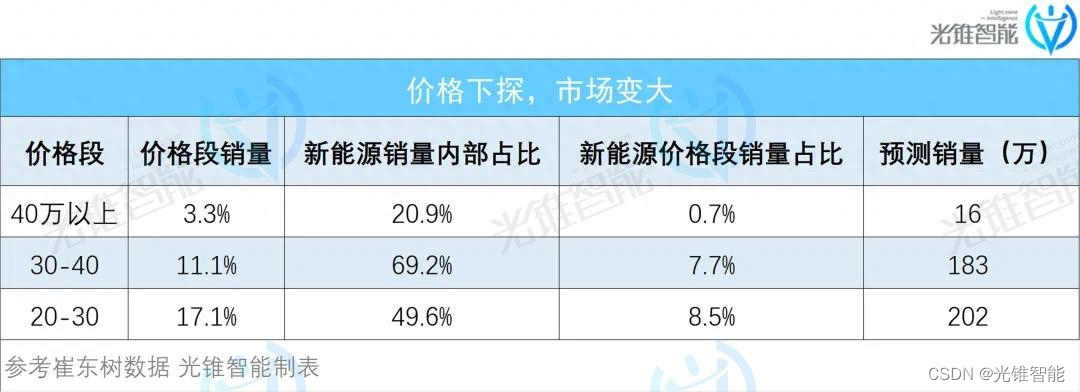
自动驾驶攻城战,华为小鹏先亮剑
点击关注 文|刘俊宏 编|苏扬、王一粟 本文为光锥智能x腾讯科技联合出品 2023年过半,城市NOA(城市领航辅助驾驶)的元年如预期中到来了吗? 8月25日,成都车展开幕,与4个月之前的上海…...
企业供应链数字化怎么做?企业数字化供应链流程落地方式
什么是供应链?简单来说,供应链是围绕客户需求,以提高产品流通各个环节的效率为目标,通过资源整合的方式来实现产品从设计、生产到销售、服务整个环节的组织形态。如同人工智能、区块链、5G等技术的发展带来的各种行业变化…...

java八股文面试[多线程]——synchronized 和lock的区别
其他差别: synchronized是隐式的加锁,lock是显式的加锁; synchronized底层采用的是objectMonitor,lock采用的AQS; synchronized在进行加锁解锁时,只有一个同步队列和一个等待队列, lock有一个同步队列,可以有多个等待队列; synchronized使用了object类的wait和noti…...

实现一个简单的控制台版用户登陆程序, 程序启动提示用户输入用户名密码. 如果用户名密码出错, 使用自定义异常的方式来处理
//密码错误异常类 public class PasswordError extends Exception {public PasswordError(String message){super(message);} }//用户名错误异常类 public class UserError extends Exception{public UserError(String message){super(message);} }import java.util.Scanner;pu…...

Java 大厂八股文面试专题-设计模式 工厂方法模式、策略模式、责任链模式
面试专题-设计模式 前言 在平时的开发中,涉及到设计模式的有两块内容,第一个是我们平时使用的框架(比如spring、mybatis等),第二个是我们自己开发业务使用的设计模式。 面试官一般比较关心的是你在开发过程中ÿ…...
Anaconda Prompt输入jupyter lab无反应
问题:Anaconda Prompt界面输入指令无反应 原因:公司电脑勒索病毒防御工具阻止了进程 解决:找到黑名单恢复进程...

JavaScript Web APIs - 05 Window对象 、本地存储
Web APIs - 05 文章目录 Web APIs - 05js组成window对象定时器-延迟函数location对象navigator对象histroy对象本地存储(今日重点)localStorage(重点)sessionStorage(了解)localStorage 存储复杂数据类型 综…...
Ansible学习笔记6
stat模块:获取文件的状态信息,类似Linux的stat状态。 获取/etc/fstab文件的状态。 [rootlocalhost tmp]# ansible group1 -m stat -a "path/etc/fstab" 192.168.17.106 | SUCCESS > {"ansible_facts": {"discovered_inter…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
