【考研数学】线性代数第四章 —— 线性方程组(2,线性方程组的通解 | 理论延伸)
文章目录
- 引言
- 四、线性方程组的通解
- 4.1 齐次线性方程组
- 4.2 非齐次线性方程组
- 五、方程组解的理论延伸
引言
承接前文,继续学习线性方程组的内容,从方程组的通解开始。
四、线性方程组的通解
4.1 齐次线性方程组
(1)基础解系 —— 设 r ( A ) = r < n r(A)=r<n r(A)=r<n ,则 A X = 0 \pmb{AX=0} AX=0 所有解构成的解向量组的极大线性无关组称为方程组 A X = 0 \pmb{AX=0} AX=0 的一个基础解系。基础解系中所含有的线性无关的解向量的个数为 ( n − r ) (n-r) (n−r) 个。
因为是 r ( A ) = n r(A)=n r(A)=n 呢?因为如果 r ( A ) = n r(A)=n r(A)=n 的话,那齐次方程就只有零解了,也没什么好讨论的。
求齐次线性方程组的基础解系时,把其系数矩阵通过初等行变换进行阶梯化(系数矩阵进行初等行变换相当于方程组的同解变形),每行第一个非零元素所在的列对应的未知数是约束变量,其余变量是自由变量,从而可以确定基础解系(最好把每行第一个非零元素化为 1 ,且其所在的列其余元素都化为零)。
举个例子,假设方程组 A X = 0 \pmb{AX=0} AX=0 的系数矩阵 A \pmb{A} A 经过初等行变换可以化为如下形式:

则 r ( A ) = 3 < 5 r(A)=3<5 r(A)=3<5 ,方程组 A X = 0 \pmb{AX=0} AX=0 的基础解系中含有 n − r = 5 − 3 = 2 n-r=5-3=2 n−r=5−3=2 个解向量,其中 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3 为约束变量, x 4 , x 5 x_4,x_5 x4,x5 为自由变量, ( x 4 , x 5 ) (x_4,x_5) (x4,x5) 分别取 ( 1 , 0 ) (1,0) (1,0) 和 ( 0 , 1 ) (0,1) (0,1) ,则基础解系为: ξ 1 = ( − 2 , 1 , − 3 , 1 , 0 ) T , ξ 2 = ( 3 , − 4 , 2 , 0 , 1 ) T . \xi_1=(-2,1,-3,1,0)^T,\xi_2=(3,-4,2,0,1)^T. ξ1=(−2,1,−3,1,0)T,ξ2=(3,−4,2,0,1)T. (2)通解 —— 设 ξ 1 , ξ 2 , … , ξ n − r \xi_1,\xi_2,\dots,\xi_{n-r} ξ1,ξ2,…,ξn−r 为齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的一个基础解系,称 k 1 ξ 1 + k 2 ξ 2 + ⋯ + k n − r ξ n − r k_1\xi_1+k_2\xi_2+\dots+k_{n-r}\xi_{n-r} k1ξ1+k2ξ2+⋯+kn−rξn−r 为齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的通解,其中 k 1 , k 2 , … , k n − r k_1,k_2,\dots,k_{n-r} k1,k2,…,kn−r 为任意常数。
4.2 非齐次线性方程组
设 r ( A ) = r ( A ‾ ) < n r(A)=r(\overline{A})<n r(A)=r(A)<n ,且 ξ 1 , ξ 2 , … , ξ n − r \xi_1,\xi_2,\dots,\xi_{n-r} ξ1,ξ2,…,ξn−r 为 A X = b \pmb{AX=b} AX=b 的导出方程组 A X = 0 \pmb{AX=0} AX=0 的一个基础解系, η 0 \pmb{\eta_0} η0 为 A X = b \pmb{AX=b} AX=b 的一个解,则 A X = b \pmb{AX=b} AX=b 的通解为 k 1 ξ 1 + k 2 ξ 2 + ⋯ + k n − r ξ n − r + η 0 , k_1\xi_1+k_2\xi_2+\dots+k_{n-r}\xi_{n-r}+\eta_0, k1ξ1+k2ξ2+⋯+kn−rξn−r+η0, 其中 k 1 , k 2 , … , k n − r k_1,k_2,\dots,k_{n-r} k1,k2,…,kn−r 为任意常数。
1,齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的基础解系不唯一,但线性无关的解向量的个数是唯一的。
2, r ( A ) = r ( A ‾ ) < n r(A)=r(\overline{A})<n r(A)=r(A)<n 时,非齐次线性方程组 A X = b \pmb{AX=b} AX=b 所有解向量的极大线性无关的向量个数为 ( n − r + 1 ) (n-r+1) (n−r+1) 个。
3,设 η 1 , η 2 , … , η n − r + 1 \eta_1,\eta_2,\dots,\eta_{n-r+1} η1,η2,…,ηn−r+1 为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的一个极大线性无关组,则其通解也可以像齐次方程那样表示为 k 1 η 1 + k 2 η 2 + ⋯ + k n − r + 1 η n − r + 1 k_1\eta_1+k_2\eta_2+\dots+k_{n-r+1}\eta_{n-r+1} k1η1+k2η2+⋯+kn−r+1ηn−r+1 ,其中 k 1 , k 2 , … , k n − r + 1 k_1,k_2,\dots,k_{n-r+1} k1,k2,…,kn−r+1 为任意常数,且 k 1 + k 2 + ⋯ + k n − r + 1 = 1. k_1+k_2+\dots+k_{n-r+1}=1. k1+k2+⋯+kn−r+1=1.
五、方程组解的理论延伸
定理 1 —— 设 A A A 是 m × n m\times n m×n 矩阵, B B B 是 n × s n\times s n×s 矩阵,若 A B = O AB=O AB=O ,则 B B B 的列向量组是方程组 A X = 0 AX=0 AX=0 的解。
证明: 令 B = ( β 1 , β 2 , … , β s ) B=(\beta_1,\beta_2,\dots,\beta_s) B=(β1,β2,…,βs),则 A B = ( A β 1 , A β 2 , … , A β s ) AB=(A\beta_1,A\beta_2,\dots,A\beta_s) AB=(Aβ1,Aβ2,…,Aβs),若 A B = O AB=O AB=O ,则 A β 1 = 0 , A β 2 = 0 … , A β s = 0 A\beta_1=0,A\beta_2=0\dots,A\beta_s=0 Aβ1=0,Aβ2=0…,Aβs=0 ,原命题得证。
定理 2 —— 设方程组 A X = 0 \pmb{AX=0} AX=0 与 B X = 0 \pmb{BX=0} BX=0 为同解方程组,则 r ( A ) = r ( B ) r(A)=r(B) r(A)=r(B) ,反之不对。
定理 3 —— 设方程组 A X = 0 \pmb{AX=0} AX=0 的解为 B X = 0 \pmb{BX=0} BX=0 的解,则 r ( A ) ≥ r ( B ) . r(A) \geq r(B). r(A)≥r(B).
1,设方程组 A X = 0 \pmb{AX=0} AX=0 的解为 B X = 0 \pmb{BX=0} BX=0 的解,但不全是,则 r ( A ) > r ( B ) . r(A) > r(B). r(A)>r(B).
2,设方程组 A X = 0 \pmb{AX=0} AX=0 的解为 B X = 0 \pmb{BX=0} BX=0 的解,且 r ( A ) = r ( B ) r(A) = r(B) r(A)=r(B) ,则两个方程组同解。
定理 4 —— 设 A X = b , B X = c \pmb{AX=b},\pmb{BX=c} AX=b,BX=c ,则线性方程组 ( A , B ) T X = ( b , c ) T (A,B)^TX=(b,c)^T (A,B)TX=(b,c)T 的解即为两个方程的公共解。
相关文章:

【考研数学】线性代数第四章 —— 线性方程组(2,线性方程组的通解 | 理论延伸)
文章目录 引言四、线性方程组的通解4.1 齐次线性方程组4.2 非齐次线性方程组 五、方程组解的理论延伸 引言 承接前文,继续学习线性方程组的内容,从方程组的通解开始。 四、线性方程组的通解 4.1 齐次线性方程组 (1)基础解系 —…...

go读取文件的几种方法
一. 整个文件读入内存 直接将数据直接读取入内存,是效率最高的一种方式,但此种方式,仅适用于小文件,对于大文件,则不适合,因为比较浪费内存 1.直接指定文化名读取 在 Go 1.16 开始,ioutil.Rea…...

ChatGPT癌症治疗“困难重重”,真假混讲难辨真假,准确有待提高
近年来,人工智能在医疗领域的应用逐渐增多,其中自然语言处理模型如ChatGPT在提供医疗建议和信息方面引起了广泛关注。然而,最新的研究表明,尽管ChatGPT在许多领域取得了成功,但它在癌症治疗方案上的准确性仍有待提高。…...
docker打包vue vite前端项目
打包vue vite 前端项目 1.打包时将测试删除 2.修改配置 3.打包项目 npm run build 显示成功(黄的也不知道是啥) 打包好的前端文件放入 4.配置 default.conf upstream wms-app {server 你自己的ip加端口 ;server 192.168.xx.xx:8080 ; } server { …...

zookeeper 查询注册的 dubbo 服务
1. 连接zookeeper 服务端 使用bin 目录下zk客户端连接服务器, ./zkCli.sh -server 127.0.0.1:2181 2. 查询Dubbo 服务 # 查询所有服务 ls /dubbo # 查询指定服务调用 ls /dubbo/服务名(接口地址)/consumers # 查询指定服务调用 ls /dubbo/服务名(接口地址)/pr…...

【每日一题】57. 插入区间
【每日一题】57. 插入区间 57. 插入区间题目描述解题思路 57. 插入区间 题目描述 给你一个 无重叠的 ,按照区间起始端点排序的区间列表。 在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可…...

youtubu视频下载和yt-dlp 使用教程
参考:https://zhuanlan.zhihu.com/p/618467617,使用 yt-dlp 下载 youtube 视频的一点体会 安装yt-dlp 1. 安装Python和ffmpeg Python:安装时把pip和添加系统环境变量都选上 ffmpeg:下载好exe文件,把目录添加到系统环…...
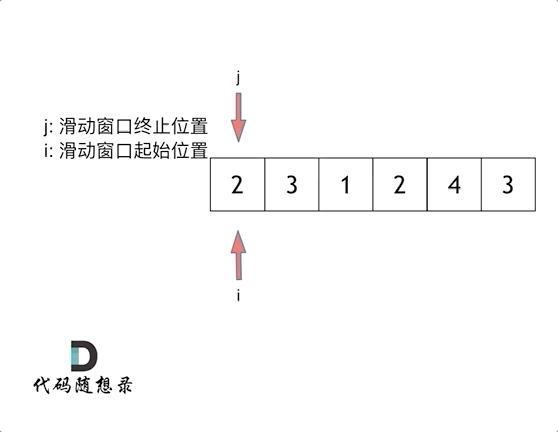
——滑动窗口
滑动窗口 所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。也可以理解为一种双指针的做法。 leetcode76 class Solution {public String minWindow(String s, String t) {char[] schars s.toCharArray();char[] tc…...
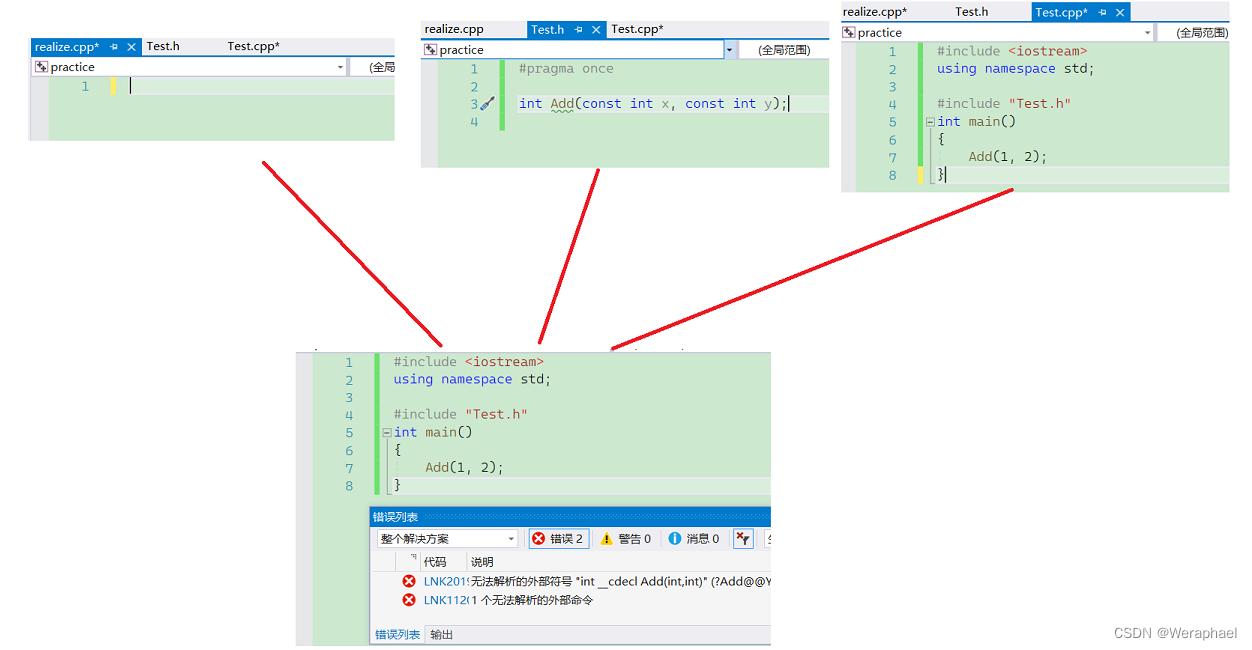
【C++进阶】模板进阶
👦个人主页:Weraphael ✍🏻作者简介:目前学习C和算法 ✈️专栏:C航路 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞…...

Vim如何清空文件
在Vim中,可以使用以下命令清空文件内容: 打开需要清空的文件:在终端中输入vim filename打开文件,其中filename是你要编辑的文件名。 进入命令模式:按下键盘上的Esc键,确保处于Vim的命令模式。(…...

问道管理:什么信号?煤飞色舞钢花溅
近期重磅利好不断,对应到A股商场,究竟哪个板块最获益,商场讨论热烈。 地产分析师:方针力度超预期,主张加仓。 银行分析师:存量房贷对银行股心情上的压制完毕,值得重视。 消费分析师ÿ…...
C# PaddleDetection yolo 印章检测
效果 项目 代码 using OpenCvSharp; using OpenCvSharp.Extensions; using Sdcb.PaddleDetection; using Sdcb.PaddleInference; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq…...

常用框架分析(7)-Flutter
框架分析(7)-Flutter 专栏介绍Flutter核心思想Flutter的特点快速开发跨平台高性能美观的用户界面 Flutter的架构框架层引擎层平台层 开发过程使用Dart语言编写代码编译成原生代码热重载工具和插件 优缺点优点跨平台开发高性能美观的用户界面热重载强大的…...

清空 Docker 容器的日志文件
删除容器中netcore控制台存储到docker日志记录 在shell命令下执行如下语句: docker ps -aq | xargs docker inspect --format{{.LogPath}} | xargs truncate -s 0 这个命令会执行以下操作: docker ps -aq:列出所有容器的ID(包括…...
01-虚拟机安装Windows Server操作系统
1、创建并配置虚拟机 2、安装操作系统 找到windows Server镜像 等待安装 3、设置密码...

应用案例 | 基于三维机器视觉的机器人麻袋拆垛应用解决方案
Part.1 项目背景 在现代物流和制造行业中,麻袋的拆垛操作是一个重要且频繁的任务。传统的麻袋拆垛工作通常由人工完成,分拣效率较低,人力成本较高,现场麻袋堆叠、变形严重,垛型不规则、不固定,严重影响分…...
)
1018 Public Bike Management 结题记录(dfs剪枝)
个人觉得直接放入代码是最管用的。 其他方法类似,题意请参考其他博主。 #include <bits/stdc.h> using namespace std; const int N 1e4 50;int maxn 2000000000; int c, n, ed, s[N], m, minlen, needn, backn, pre[N]; bool flag, book[N]; vector<p…...

C++ deque底层原理
deque底层原理 一、目的二、底层实现三、原理图四、类结构五、push_back六、pop_back 一、目的 实现双端数组 二、底层实现 双向开口的连续线性空间 三、原理图 四、类结构 class deque : protected Deque base _Deque_base._Deque_impl M_map 指针数组 _M_map_size …...

打破对ChatGPT的依赖以及如何应对ChatGPT的错误和幻觉
OpenAI的ChatGPT是第一个真正流行的生成式AI工具,但它可能不是最好的。现在是时候扩大你的AI视野了。 ChatGPT成为了基于大语言模型(LLM)的聊天机器人的同义词。但是现在是时候停止对ChatGPT的痴迷,开始发现这个新世界中强大的替代品了。 首先&a…...
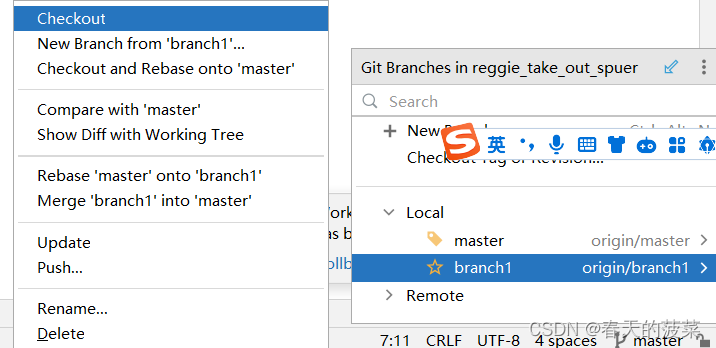
【git】【IDEA】在idea中使用git
目录 一、 在IDEA中配置git 二、 获取git仓库 2.1 本次初始化仓库 2.2 从远程仓库克隆 三、 本地仓库操作 3.1 将文件加入暂存区 3.2 将暂存区的文件提交到版本库 3.3 快捷键 使用快捷键 实现加入到暂存区与提交到版本库 3.4 查看日志 Show History 四、 远程仓库操…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...

【2D与3D SLAM中的扫描匹配算法全面解析】
引言 扫描匹配(Scan Matching)是同步定位与地图构建(SLAM)系统中的核心组件,它通过对齐连续的传感器观测数据来估计机器人的运动。本文将深入探讨2D和3D SLAM中的各种扫描匹配算法,包括数学原理、实现细节以及实际应用中的性能对比,特别关注…...

今日行情明日机会——20250609
上证指数放量上涨,接近3400点,个股涨多跌少。 深证放量上涨,但有个小上影线,相对上证走势更弱。 2025年6月9日涨停股主要行业方向分析(基于最新图片数据) 1. 医药(11家涨停) 代表标…...
