原神世界中的顺序表:派蒙的趣味数据结构讲解
派蒙,那个总是带着疑问眼神的小家伙,是原神世界中的小精灵。他总是充满好奇心,无论是对新的冒险者,还是对各种奇妙的现象。而他的另一个身份,则是原神世界中的数据结构大师。
一天,派蒙遇到了旅行者小森,他带着一肚子的疑问和困惑。
小森:“派蒙,我一直在想,你们这些小精灵是怎么记住那么多东西的?还有,你们是怎么管理那些任务的?”
派蒙眼睛一亮:“哎呀,小森,你问的问题非常好。你知道吗,我们小精灵使用的一种数据结构叫做顺序表。你知道什么是顺序表吗?”
小森摇摇头:“我不太清楚。”
派蒙得意地笑起来:“那就让我来告诉你吧。顺序表是一种线性数据结构,它按照元素的顺序进行存储和访问。就像我们在原神世界中按照顺序完成任务一样,每个任务都有前一个和后一个任务,形成了一个顺序表。”
小森点点头:“我明白了,那这种数据结构有什么优点呢?”
派蒙答道:“顺序表的优点在于它可以快速地访问元素。因为元素是按照顺序存储的,所以我们可以通过索引直接访问任何元素。这就像你可以通过任务列表直接跳转到任何一个任务一样。”
小森:“听起来很有用。”
派蒙:“是的,而且顺序表还便于进行插入和删除操作。只要保留足够的空间,我们就可以在表的任何位置插入或删除元素。这就像我们在冒险过程中随时可以接受或放弃任务一样。”
小森:“我明白了,这种数据结构在我们现实生活中也有应用吗?”
派蒙笑得更欢了:“当然有啦。顺序表在计算机科学中有广泛的应用,例如操作系统中的进程调度、文件系统、数据库等等。可以说,没有顺序表,就没有我们原神世界的顺畅运行。”
小森对派蒙的博学感到敬佩,同时也对自己的提问感到满意。他决定把派蒙的这些知识应用到自己的冒险旅程中。
然而,派蒙并没有结束他的讲解。他神秘地眨眨眼:“此外,顺序表还有许多变种和优化。例如,链表、循环链表、哈希表等等。这些高级的数据结构可以帮助我们更高效地处理数据和任务。”
小森听得津津有味,他决定要深入研究这些神奇的数据结构,以便更好地完成自己的使命。
派蒙继续讲解顺序表的结构:“顺序表是一种连续的线性结构,它的元素按照顺序存储在一个连续的内存空间中。每个元素都有一个固定的大小,并且相邻元素之间有一定的空隙。顺序表的优点是访问元素速度快,因为可以通过索引直接访问任意元素。但是,顺序表在插入和删除元素时可能会比较慢,因为需要移动大量的元素。”
小森问:“那么,顺序表有哪些变种和优化呢?”
派蒙答道:“顺序表的变种和优化有很多,比如链表、循环链表、哈希表等等。链表是一种非连续的线性结构,它的元素可以存储在不同的内存空间中。链表的优点是插入和删除元素速度快,因为只需要修改指针即可。但是,访问元素速度较慢,因为需要遍历整个链表。”
小森又问:“那么,顺序表和链表有什么区别呢?”
派蒙解释道:“顺序表和链表的区别在于它们的存储方式和访问方式。顺序表是连续的线性结构,元素存储在一块连续的内存空间中,访问元素速度快。而链表是非连续的线性结构,元素可以存储在不同的内存空间中,访问元素速度较慢,但是插入和删除元素速度快。”
派蒙继续讲解顺序表的初始化:“顺序表的初始化是根据其大小,在内存中分配一块连续的空间,并将空间中的元素初始化为默认值。如果顺序表的大小超过了实际需要的元素数量,那么多余的空间将被浪费。如果顺序表的大小小于实际需要的元素数量,那么顺序表可能会发生溢出。”
小森问:“那么如何确定顺序表的大小呢?”
派蒙答道:“确定顺序表的大小需要根据实际情况进行权衡。如果预计元素数量很多,但是不确定具体数量,可以考虑将顺序表的大小设置得较大一些,以避免频繁扩容。如果预计元素数量较少,可以将顺序表的大小设置得较小一些,以节省空间。”
小森又问:“那么顺序表的扩容是什么意思?”
派蒙解释道:“顺序表的扩容是指当顺序表的空间不足以容纳更多的元素时,需要重新分配一块更大的空间,并将原有元素复制到新的空间中。扩容可能会带来一定的开销,因此需要在空间效率和时间效率之间进行权衡。”
派蒙继续讲解顺序表的尾插操作:“尾插操作对于顺序表来说非常简单,只需要将新元素放到顺序表的末尾即可。这个操作在原神世界中也非常常见,比如接受新的任务或者添加新的装备。顺序表的尾插操作时间复杂度是O(1),因为这个操作不需要移动其他元素。”
小森问:“那么顺序表尾插操作之后,如果要删除末尾的元素,需要怎么做呢?”
派蒙答道:“如果要删除顺序表末尾的元素,只需要将顺序表的末尾元素覆盖掉即可。这个操作在原神世界中也非常常见,比如放弃已经接受的任务或者卸下已经装备的物品。”
小森又问:“那么顺序表的尾插操作和删除操作对顺序表有什么影响呢?”
派蒙解释道:“顺序表的尾插操作和删除操作并不会改变顺序表的大小和元素数量,只是改变了元素的值。如果顺序表的元素是用来存储任务或者装备的信息,那么尾插操作可以增加新的任务或者装备,删除操作可以取消已经接受的任务或者卸下已经装备的物品。这些操作可以帮助我们更好地管理任务和装备。”
派蒙继续讲解顺序表的访问全部元素:“顺序表是一种线性数据结构,它按照元素的顺序存储在连续的内存空间中。因此,我们可以很容易地访问顺序表中的任意元素。在顺序表中,访问任意元素的时间复杂度都是O(n),因为需要从头到尾遍历整个顺序表。”
小森问:“那么,有没有更高效的访问方式呢?”
派蒙答道:“对于顺序表来说,访问任意元素的时间复杂度都是O(n),这是因为它需要从头到尾遍历整个顺序表。但是,如果顺序表是有序的,可以使用二分查找等算法来快速查找特定元素。这些算法可以将查找时间复杂度降低到O(log n)。不过,这些算法需要顺序表是有序的,因此在原神世界中并不是很常用。”
小森又问:“那么在原神世界中,我们还是需要遍历整个顺序表吗?”
派蒙解释道:“在原神世界中,如果我们需要访问顺序表中的所有元素,我们确实需要从头到尾遍历整个顺序表。但是,这种操作并不常见,因为在原神世界中,我们通常只需要访问特定的元素,而不是所有元素。”
小森听了派蒙的解释,对顺序表的访问全部元素有了更深入的了解。他决定在需要访问顺序表中的所有元素时
派蒙继续讲解顺序表的插入元素:“顺序表的插入操作是指在顺序表的任意位置插入一个新的元素。对于顺序表来说,插入操作稍微复杂一些,因为它需要移动插入位置后面的元素。顺序表插入元素的时间复杂度是O(n),因为需要移动所有后面的元素。”
小森问:“那么顺序表插入元素需要注意哪些问题呢?”
派蒙答道:“顺序表插入元素需要注意以下几点:首先,如果要插入的位置已经在原有元素的范围内,需要将原有元素向后移动,以腾出空间。其次,如果要插入的位置超过了顺序表的末尾,需要将顺序表的大小扩展到足够大,以容纳新的元素。最后,如果要插入的位置在两个元素的中间,需要将这两个元素之间的空间填充为默认值。”
小森又问:“那么顺序表插入元素和删除元素有什么不同呢?”
派蒙解释道:“顺序表插入元素和删除元素都是顺序表的常用操作,它们的时间复杂度都是O(n)。但是,插入操作是将新元素插入到顺序表中,需要移动插入位置后面的元素;而删除操作则是删除顺序表中的某个元素,需要移动删除元素后面的元素。在原神世界中,插入操作可能比较常见,比如接受新的任务或者添加新的装备;而删除操作可能比较少见,因为任务和装备一旦删除就无法恢复。”
小森听了派蒙的解释,对顺序表的插入元素有了更深入的了解。他决定在需要接受新的任务或者添加新的装备时,使用顺序表的插入操作,并在需要删除任务或者卸下装备时,使用顺序表的删除操作。这样可以更好地管理任务和装备,让冒险更加顺畅。
派蒙继续讲解顺序表判断是否满了:“顺序表判断是否满了是根据其大小来判断的。如果顺序表的大小超过了其最大容量,那么就可以认为该顺序表已经满了。”
小森问:“那么如何判断顺序表的大小呢?”
派蒙答道:“顺序表的大小可以通过其长度来判断。如果顺序表的长度等于其最大容量,那么就可以认为该顺序表已经满了。”
小森又问:“那么顺序表的最大容量是如何设定的呢?”
派蒙解释道:“顺序表的最大容量是根据实际情况进行设定的。在设计顺序表时,可以根据需要设定一个合适的最大容量。如果预计元素数量很多,可以将最大容量设置得较大一些,以避免频繁扩容。如果预计元素数量较少,可以将最大容量设置得较小一些,以节省空间。”
派蒙继续讲解顺序表的删除操作:“顺序表的删除操作是指在顺序表中删除某个元素。对于顺序表来说,删除操作稍微复杂一些,因为它需要移动删除元素后面的元素。顺序表删除操作的时间复杂度是O(n),因为需要移动所有后面的元素。”
小森问:“那么顺序表删除操作需要注意哪些问题呢?”
派蒙答道:“顺序表删除操作需要注意以下几点:首先,如果要删除的元素在顺序表中不存在,需要给出相应的提示。其次,如果要删除的元素在顺序表的末尾,可以直接将末尾元素覆盖掉。最后,如果要删除的元素在顺序表的中间,需要将该元素后面的所有元素向前移动一位。”
小森又问:“那么顺序表删除操作和插入操作有什么不同呢?”
派蒙解释道:“顺序表删除操作和插入操作都是顺序表的常用操作,它们的时间复杂度都是O(n)。但是,删除操作是从顺序表中删除某个元素,需要移动删除元素后面的元素;而插入操作则是将新元素插入到顺序表中,需要移动插入位置后面的元素。在原神世界中,删除操作可能比较少见,因为任务和装备一旦删除就无法恢复;而插入操作可能比较常见,比如接受新的任务或者添加新的装备。”
小森听了派蒙的解释,对顺序表的删除操作有了更深入的了解。他决定在使用顺序表时,需要注意其删除操作的实现细节,以避免出现错误。
派蒙继续讲解顺序表的查找操作:“顺序表的查找操作是指在顺序表中查找某个元素。对于顺序表来说,查找操作非常简单,只需要从顺序表的头部开始逐个比较元素的值即可。如果找到了目标元素,返回其索引;如果未找到,返回-1。顺序表查找操作的时间复杂度是O(n),因为需要遍历整个顺序表。”
小森问:“那么顺序表查找操作需要注意哪些问题呢?”
派蒙答道:“顺序表查找操作需要注意以下几点:首先,如果要查找的元素在顺序表中不存在,需要给出相应的提示。其次,如果要查找的元素在顺序表的末尾,可以直接返回其索引。最后,如果要查找的元素在顺序表的中间,需要从头部开始逐个比较元素的值。”
小森又问:“那么顺序表查找操作和插入操作有什么不同呢?”
派蒙解释道:“顺序表查找操作和插入操作都是顺序表的常用操作,但是它们的目的和方式不同。查找操作是在顺序表中查找某个元素,并返回其索引;而插入操作则是将新元素插入到顺序表中,需要移动插入位置后面的元素。在原神世界中,查找操作可能比较常见,比如查找任务或者装备;而插入操作可能比较少见,因为任务和装备一旦删除就无法恢复。”
派蒙继续讲解顺序表元素记录个数:“顺序表中元素的个数可以通过其长度或者计数器来记录。顺序表的长度是指顺序表中元素的数量,可以直接通过顺序表头部的属性来获取。顺序表的计数器是一个单独的变量,用于记录顺序表中元素的个数。当插入元素时,计数器加一;当删除元素时,计数器减一。”
小森问:“那么顺序表元素记录个数需要注意哪些问题呢?”
派蒙答道:“顺序表元素记录个数需要注意以下几点:首先,当插入元素时,需要更新计数器,同时可能需要移动插入位置后面的元素。其次,当删除元素时,需要更新计数器,同时可能需要移动删除元素后面的元素。最后,需要保证计数器的正确性和及时性,以避免出现错误。”
小森又问:“那么顺序表元素记录个数和顺序表的其他操作有什么关系呢?”
派蒙解释道:“顺序表元素记录个数是顺序表的基本操作之一,它与顺序表的插入操作、删除操作等都有关系。通过记录元素的个数,可以更好地管理顺序表中的元素,比如判断顺序表是否已满、是否为空等。同时,元素的插入和删除操作也会影响元素的个数,因此需要在操作时注意更新计数器。”
派蒙继续讲解获取某个元素:“在顺序表中获取某个元素可以通过其索引实现。如果索引是有效的(即在0到n-1之间,其中n是顺序表的长度),则可以直接通过索引访问顺序表中的元素。如果索引无效,则需要给出相应的提示。”
小森问:“那么获取顺序表中某个元素需要注意哪些问题呢?”
派蒙答道:“获取顺序表中某个元素需要注意以下几点:首先,需要确保索引的有效性,即索引必须在0到n-1之间。其次,如果索引无效,需要给出相应的提示,比如返回一个空值或者错误码。最后,在获取元素时需要注意顺序表的大小和边界,以避免出现越界等错误。”
小森又问:“那么获取顺序表中某个元素和顺序表的其他操作有什么关系呢?”
派蒙解释道:“获取顺序表中某个元素是顺序表的基本操作之一,它与顺序表的插入操作、删除操作等都有关系。通过获取元素,可以更好地管理顺序表中的元素,比如获取某个任务或者装备的信息。同时,元素的插入和删除操作也会影响元素的索引,因此需要在操作时注意更新索引。”
派蒙继续讲解销毁顺序表:“销毁顺序表是指将顺序表中的所有元素删除,并释放其内存空间。销毁顺序表的操作需要在顺序表的末尾进行,将顺序表的长度设为0,并释放内存空间。”
小森问:“那么销毁顺序表需要注意哪些问题呢?”
派蒙答道:“销毁顺序表需要注意以下几点:首先,需要确保顺序表中的所有元素都被删除,避免出现内存泄漏。其次,如果顺序表中存储了重要的数据,需要将其保存或备份,以防止数据丢失。最后,在销毁顺序表后,需要释放其内存空间,以避免内存泄漏。”
小森又问:“那么销毁顺序表和顺序表的其他操作有什么关系呢?”
派蒙解释道:“销毁顺序表是顺序表的常用操作之一,它与顺序表的插入操作、删除操作等都有关系。通过销毁顺序表,可以更好地管理顺序表中的元素,比如在不需要顺序表时释放其内存空间。同时,元素的插入和删除操作也会影响顺序表的内存使用情况,因此需要在操作时注意内存管理。”
相关文章:

原神世界中的顺序表:派蒙的趣味数据结构讲解
派蒙,那个总是带着疑问眼神的小家伙,是原神世界中的小精灵。他总是充满好奇心,无论是对新的冒险者,还是对各种奇妙的现象。而他的另一个身份,则是原神世界中的数据结构大师。 一天,派蒙遇到了旅行者小森&a…...

电脑入门:路由器 基本设置操作说明
路由器 基本设置操作说明 首先我们我设置路由器,就需要先登录路由器, 那么怎样登路由器啊? 登录路由器的方法是 在ie的地址栏输入:http://192.168.1.1 输入完成以后直接回车 那么如果你输入正确 这个时候就应该听到有用户名的提示 呵呵 这是怎么回事啊? 不要召集 首…...

搜索与图论-拓扑序列
为什么记录呢 因为不记录全忘了 虽然记了也不一定会看 有向无环图一定有拓扑序列邮箱无环图 - 拓扑图 入度为0的点作为起点入度为0的点入队列枚举出边 t->j删掉当前边,t->j . j的入度减1判断j的入度是否为0,来判断是否加入队列 有环: …...

「MySQL-05」MySQL Workbench的下载和使用
目录 一、MySQL workbench的下载和安装 1. MySQL workbench介绍 2. 到MySQL官网下载mysql workbench 3. 安装workbench 二、创建能远程登录的用户并授权 1. 创建用户oj_client 2. 创建oj数据库 3. 给用户授权 4. 在Linux上登录用户oj_client检查其是否能操作oj数据库 三、使用…...

编译期jni类型转换成字符串
背景: 例如android jni 方法的签名, 这个需要每个用户都要知道具体类型,转化成签名, 要想写好签名, 必须很熟悉 类型对应的签名, 尤其java类对象要加个L, 本文将介绍怎么在编译期过程把类型转化成字符, 多个类型在尽性拼接. 定义基础数据结构 template<char ... ch> str…...

优秀的ui设计作品(合集)
UI设计师需要了解的九个Tips 1.图片类APP排版突破 规则是死的,人是活的。很多时候,如果需求是比较宽要尝试突破原则,用一些另类的排版方式,其实也是做好设计的本质。在图片类app中,错落一些的排版会使你的作品更有魅力…...

【c/c++】c和cpp混合编译
c和cpp混合编译 #ifdef __cplusplus extern "C" { #endifextern int test(int, int);#ifdef __cplusplus } #endif在这段代码中,#ifdef __cplusplus 和 #endif 之间的代码是为了在 C 中使用 C 语言的函数声明和定义时,确保编译器正确地处理 C…...

springboot定制banner
这里有几个定制banner的网站 Text to ASCII Art Generator (TAAG) ASCII Generator IMG2TXT: ASCII Art Made Easy!...
)
Qt 入门实战教程(目录)
为何我要写Qt入门教程 前置课程 《C自学精简实践教程》 教程特点 1 面向企业开发,你在这里学到的任何一步操作,都会直接在企业里用到。 2 注重设计思路训练,抽象分析问题的能力。 Qt 安装 1.1 Windows Qt 5.12.10下载与安装 1.2 我们…...
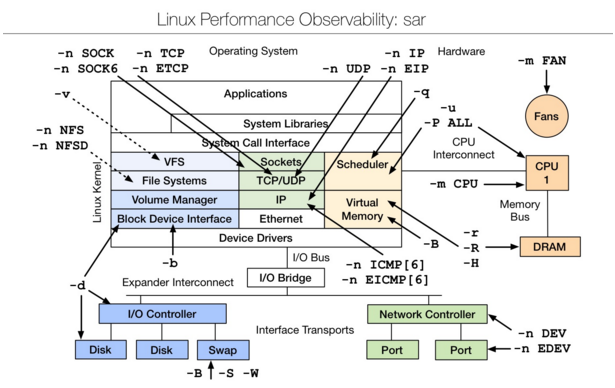
Ceph入门到精通-Lunix性能分析工具汇总
出于对Linux操作系统的兴趣,以及对底层知识的强烈欲望,因此整理了这篇文章。本文也可以作为检验基础知识的指标,另外文章涵盖了一个系统的方方面面。如果没有完善的计算机系统知识,网络知识和操作系统知识,文档中的工具…...

服务器端使用django websocket,客户端使用uniapp 请问服务端和客户端群组互发消息的代码怎么写的参考笔记
2023/8/29 19:21:11 服务器端使用django websocket,客户端使用uniapp 请问服务端和客户端群组互发消息的代码怎么写 2023/8/29 19:22:25 在服务器端使用Django WebSocket和客户端使用Uniapp的情况下,以下是代码示例来实现服务器端和客户端之间的群组互发消息。 …...

【考研数学】线性代数第四章 —— 线性方程组(2,线性方程组的通解 | 理论延伸)
文章目录 引言四、线性方程组的通解4.1 齐次线性方程组4.2 非齐次线性方程组 五、方程组解的理论延伸 引言 承接前文,继续学习线性方程组的内容,从方程组的通解开始。 四、线性方程组的通解 4.1 齐次线性方程组 (1)基础解系 —…...

go读取文件的几种方法
一. 整个文件读入内存 直接将数据直接读取入内存,是效率最高的一种方式,但此种方式,仅适用于小文件,对于大文件,则不适合,因为比较浪费内存 1.直接指定文化名读取 在 Go 1.16 开始,ioutil.Rea…...

ChatGPT癌症治疗“困难重重”,真假混讲难辨真假,准确有待提高
近年来,人工智能在医疗领域的应用逐渐增多,其中自然语言处理模型如ChatGPT在提供医疗建议和信息方面引起了广泛关注。然而,最新的研究表明,尽管ChatGPT在许多领域取得了成功,但它在癌症治疗方案上的准确性仍有待提高。…...
docker打包vue vite前端项目
打包vue vite 前端项目 1.打包时将测试删除 2.修改配置 3.打包项目 npm run build 显示成功(黄的也不知道是啥) 打包好的前端文件放入 4.配置 default.conf upstream wms-app {server 你自己的ip加端口 ;server 192.168.xx.xx:8080 ; } server { …...

zookeeper 查询注册的 dubbo 服务
1. 连接zookeeper 服务端 使用bin 目录下zk客户端连接服务器, ./zkCli.sh -server 127.0.0.1:2181 2. 查询Dubbo 服务 # 查询所有服务 ls /dubbo # 查询指定服务调用 ls /dubbo/服务名(接口地址)/consumers # 查询指定服务调用 ls /dubbo/服务名(接口地址)/pr…...

【每日一题】57. 插入区间
【每日一题】57. 插入区间 57. 插入区间题目描述解题思路 57. 插入区间 题目描述 给你一个 无重叠的 ,按照区间起始端点排序的区间列表。 在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可…...

youtubu视频下载和yt-dlp 使用教程
参考:https://zhuanlan.zhihu.com/p/618467617,使用 yt-dlp 下载 youtube 视频的一点体会 安装yt-dlp 1. 安装Python和ffmpeg Python:安装时把pip和添加系统环境变量都选上 ffmpeg:下载好exe文件,把目录添加到系统环…...
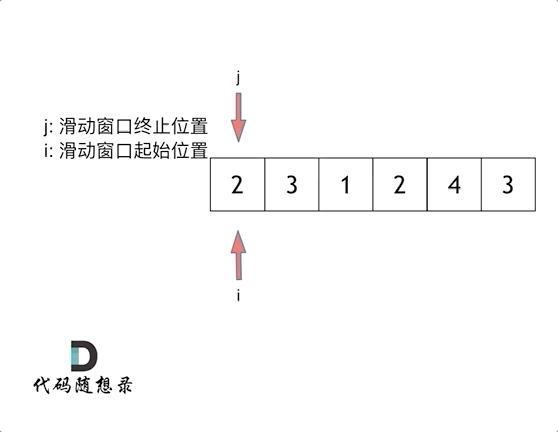
——滑动窗口
滑动窗口 所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。也可以理解为一种双指针的做法。 leetcode76 class Solution {public String minWindow(String s, String t) {char[] schars s.toCharArray();char[] tc…...
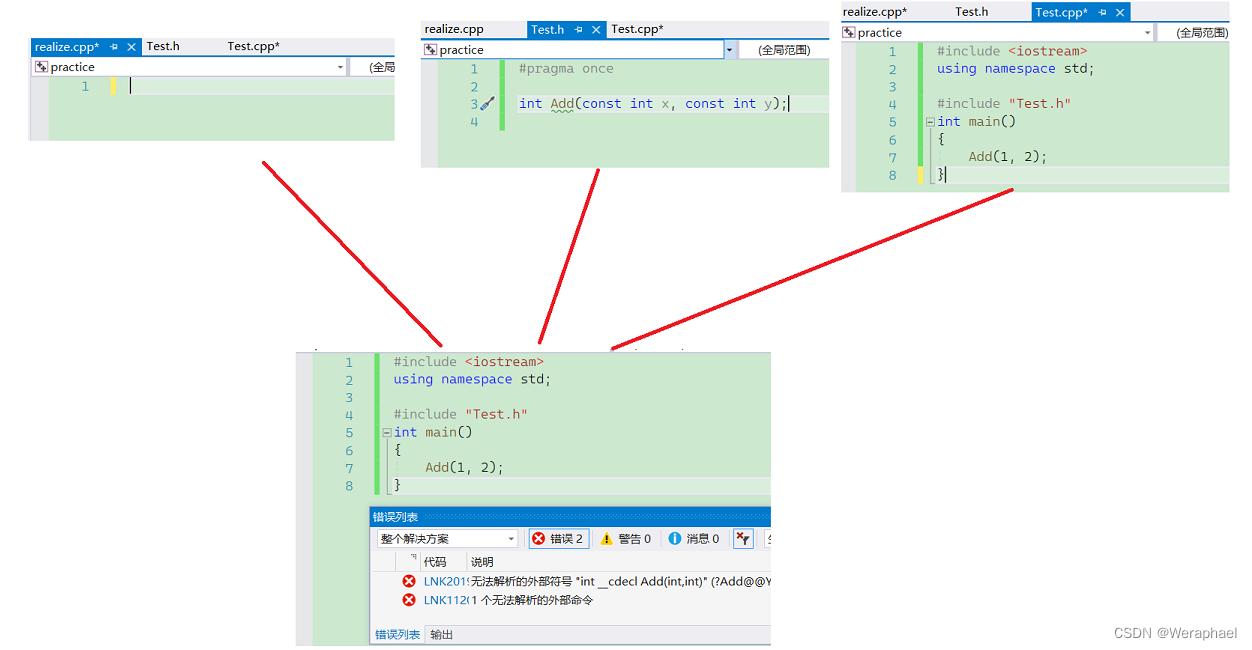
【C++进阶】模板进阶
👦个人主页:Weraphael ✍🏻作者简介:目前学习C和算法 ✈️专栏:C航路 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
