LeetCode 23 合并 K 个升序链表
LeetCode 23 合并 K 个升序链表
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/merge-k-sorted-lists/description/
博主Github:https://github.com/GDUT-Rp/LeetCode
题目:
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[1->4->5,1->3->4,2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例2:
输入:lists = []
输出:[]
示例3:
输入:lists = [[]]
输出:[]
提示:
- k == lists.length
- 0 <= k <= 1 0 4 10^4 104
- 0 <= lists[i].length <= 500
- − 1 0 4 -10^4 −104 <= lists[i][j] <= 1 0 4 10^4 104
- lists[i] 按 升序 排列
- lists[i].length 的总和不超过 10^4
解题思路:
方法一:顺序合并
用一个变量 ans 来维护以及合并的链表,第 i 次循环把第 i 个链表和 ans 合并,答案保存到 ans 中。
Golang
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/
func mergeKLists(lists []*ListNode) *ListNode {var ans *ListNodefor i:=0; i<len(lists); i++ {ans = mergeTwoLists(ans, lists[i])}return ans
}func mergeTwoLists(a *ListNode, b *ListNode) *ListNode {if a == nil {return b}if b == nil {return a}var head ListNodetail := &headfor (a != nil && b != nil) {if a.Val < b.Val {tail.Next = aa = a.Next} else {tail.Next = bb = b.Next}tail = tail.Next}if a != nil {tail.Next = a} else {tail.Next = b}return head.Next
}
C++
class Solution {
public:ListNode* mergeTwoLists(ListNode *a, ListNode *b) {if ((!a) || (!b)) return a ? a : b;ListNode head, *tail = &head, *aPtr = a, *bPtr = b;while (aPtr && bPtr) {if (aPtr->val < bPtr->val) {tail->next = aPtr; aPtr = aPtr->next;} else {tail->next = bPtr; bPtr = bPtr->next;}tail = tail->next;}tail->next = (aPtr ? aPtr : bPtr);return head.next;}ListNode* mergeKLists(vector<ListNode*>& lists) {ListNode *ans = nullptr;for (size_t i = 0; i < lists.size(); ++i) {ans = mergeTwoLists(ans, lists[i]);}return ans;}
};
Java
class Solution {public ListNode mergeKLists(ListNode[] lists) {ListNode ans = null;for (int i = 0; i < lists.length; ++i) {ans = mergeTwoLists(ans, lists[i]);}return ans;}public ListNode mergeTwoLists(ListNode a, ListNode b) {if (a == null || b == null) {return a != null ? a : b;}ListNode head = new ListNode(0);ListNode tail = head, aPtr = a, bPtr = b;while (aPtr != null && bPtr != null) {if (aPtr.val < bPtr.val) {tail.next = aPtr;aPtr = aPtr.next;} else {tail.next = bPtr;bPtr = bPtr.next;}tail = tail.next;}tail.next = (aPtr != null ? aPtr : bPtr);return head.next;}
}
复杂度分析
时间复杂度: 假设每个链表的最长长度是 n。在第一次合并后,ans 的长度为 n;第二次合并后,ans 的长度为 2n,第 i 次合并后,ans 的长度为 i×n。第 i 次合并的时间代价是 O(n+(i−1)×n)=O(i×n),那么总的时间代价为 O ( ∑ i = 1 k ( i × n ) ) = O ( ( 1 + k ) ⋅ k 2 × n ) = O ( k 2 n ) O(\sum_{i = 1}^{k} (i \times n)) = O(\frac{(1 + k)\cdot k}{2} \times n) = O(k^2 n) O(∑i=1k(i×n))=O(2(1+k)⋅k×n)=O(k2n),故渐进时间复杂度为 O ( k 2 n ) O(k^2 n) O(k2n)。
空间复杂度 O(1) 。
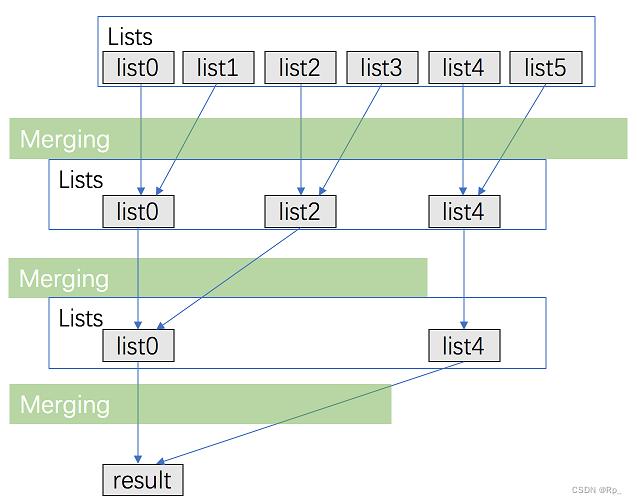
方法二:分治合并
考虑优化方法一,用分治的方法进行合并。
- 将 kkk 个链表配对并将同一对中的链表合并;
- 第一轮合并以后, k 个链表被合并成了 k 2 \frac{k}{2} 2k 个链表,平均长度为 2 n k \frac{2n}{k} k2n,然后是 k 4 \frac{k}{4} 4k 个链表, k 8 \frac{k}{8} 8k 个链表等等;
- 重复这一过程,直到我们得到了最终的有序链表。
Golang
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/
func mergeKLists(lists []*ListNode) *ListNode {return merge(lists, 0, len(lists) - 1)
}func merge(lists []*ListNode, left, right int) *ListNode {if left == right {return lists[left]}if left > right {return nil}mid := (left + right) >> 1return mergeTwoLists(merge(lists, left, mid), merge(lists, mid+1, right))
}func mergeTwoLists(a *ListNode, b *ListNode) *ListNode {if a == nil {return b}if b == nil {return a}var head ListNodetail := &headfor (a != nil && b != nil) {if a.Val < b.Val {tail.Next = aa = a.Next} else {tail.Next = bb = b.Next}tail = tail.Next}if a != nil {tail.Next = a} else {tail.Next = b}return head.Next
}
C++
class Solution {
public:ListNode* mergeTwoLists(ListNode *a, ListNode *b) {if ((!a) || (!b)) return a ? a : b;ListNode head, *tail = &head, *aPtr = a, *bPtr = b;while (aPtr && bPtr) {if (aPtr->val < bPtr->val) {tail->next = aPtr; aPtr = aPtr->next;} else {tail->next = bPtr; bPtr = bPtr->next;}tail = tail->next;}tail->next = (aPtr ? aPtr : bPtr);return head.next;}ListNode* merge(vector <ListNode*> &lists, int l, int r) {if (l == r) return lists[l];if (l > r) return nullptr;int mid = (l + r) >> 1;return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));}ListNode* mergeKLists(vector<ListNode*>& lists) {return merge(lists, 0, lists.size() - 1);}
};
Java
class Solution {public ListNode mergeKLists(ListNode[] lists) {return merge(lists, 0, lists.length - 1);}public ListNode merge(ListNode[] lists, int l, int r) {if (l == r) {return lists[l];}if (l > r) {return null;}int mid = (l + r) >> 1;return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));}public ListNode mergeTwoLists(ListNode a, ListNode b) {if (a == null || b == null) {return a != null ? a : b;}ListNode head = new ListNode(0);ListNode tail = head, aPtr = a, bPtr = b;while (aPtr != null && bPtr != null) {if (aPtr.val < bPtr.val) {tail.next = aPtr;aPtr = aPtr.next;} else {tail.next = bPtr;bPtr = bPtr.next;}tail = tail.next;}tail.next = (aPtr != null ? aPtr : bPtr);return head.next;}
}
时间复杂度:考虑递归「向上回升」的过程——第一轮合并 k 2 \frac{k}{2} 2k 组链表,每一组的时间代价是 O ( 2 n ) O(2n) O(2n);第二轮合并 k 4 \frac{k}{4} 4k 组链表,每一组的时间代价是 O ( 4 n ) O(4n) O(4n)…所以总的时间代价是 O ( ∑ i = 1 ∞ k 2 i × 2 i n ) = O ( k n × log k ) O(\sum_{i = 1}^{\infty} \frac{k}{2^i} \times 2^i n) = O(kn \times \log k) O(∑i=1∞2ik×2in)=O(kn×logk),故渐进时间复杂度为 O ( k n × log k ) O(kn \times \log k) O(kn×logk)
空间复杂度:递归会使用到 O ( log k ) O(\log k) O(logk) 空间代价的栈空间。
方法三:使用优先队列/最小堆合并
这个方法和前两种方法的思路有所不同
我们需要维护当前每个链表没有被合并的元素的最前面一个, k k k 个链表就最多有 k k k 个满足这样条件的元素,每次在这些元素里面选取 val 属性最小的元素合并到答案中。
在选取最小元素的时候,我们可以用优先队列/最小堆来优化这个过程。
Golang
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/import "container/heap"type Status struct {Val intPtr *ListNode
}type PriorityQueue []*Statusfunc (pq PriorityQueue) Len() int {return len(pq)
}func (pq PriorityQueue) Less(i, j int) bool {return pq[i].Val < pq[j].Val
}func (pq PriorityQueue) Swap(i, j int) {pq[i], pq[j] = pq[j], pq[i]
}func (pq *PriorityQueue) Push(x interface{}) {*pq = append(*pq, x.(*Status))
}func (pq *PriorityQueue) Pop() interface{} {old := *pqn := len(old)item := old[n-1]old[n-1] = nil*pq = old[0 : n-1]return item
}func mergeKLists(lists []*ListNode) *ListNode {var q PriorityQueueheap.Init(&q)for _, node := range lists {// 每个链表第一个都放进这个堆if node != nil {heap.Push(&q, &Status{Val: node.Val, Ptr: node})}}var head ListNodetail := &headfor q.Len() > 0 {// 取出最小的f := heap.Pop(&q).(*Status)tail.Next = f.Ptrtail = tail.Next// 只要所取的节点后面还要数据if f.Ptr.Next != nil {// 就放进堆里来heap.Push(&q, &Status{Val: f.Ptr.Next.Val, Ptr: f.Ptr.Next})}}return head.Next
}
Java
class Solution {class Status implements Comparable<Status> {int val;ListNode ptr;Status(int val, ListNode ptr) {this.val = val;this.ptr = ptr;}public int compareTo(Status status2) {return this.val - status2.val;}}PriorityQueue<Status> queue = new PriorityQueue<Status>();public ListNode mergeKLists(ListNode[] lists) {for (ListNode node: lists) {if (node != null) {queue.offer(new Status(node.val, node));}}ListNode head = new ListNode(0);ListNode tail = head;while (!queue.isEmpty()) {Status f = queue.poll();tail.next = f.ptr;tail = tail.next;if (f.ptr.next != null) {queue.offer(new Status(f.ptr.next.val, f.ptr.next));}}return head.next;}
}
C++
class Solution {
public:struct Status {int val;ListNode *ptr;bool operator < (const Status &rhs) const {return val > rhs.val;}};priority_queue <Status> q;ListNode* mergeKLists(vector<ListNode*>& lists) {for (auto node: lists) {if (node) q.push({node->val, node});}ListNode head, *tail = &head;while (!q.empty()) {auto f = q.top(); q.pop();tail->next = f.ptr; tail = tail->next;if (f.ptr->next) q.push({f.ptr->next->val, f.ptr->next});}return head.next;}
};
复杂度分析
时间复杂度:考虑优先队列中的元素不超过 k k k 个,那么插入和删除的时间代价为 ¥O(\log k)$,这里最多有 k n kn kn 个点,对于每个点都被插入删除各一次,故总的时间代价即渐进时间复杂度为 O ( k n × log k ) O(kn \times \log k) O(kn×logk)。
空间复杂度:这里用了优先队列,优先队列中的元素不超过 k k k 个,故渐进空间复杂度为 O ( k ) O(k) O(k)。
相关文章:

LeetCode 23 合并 K 个升序链表
LeetCode 23 合并 K 个升序链表 来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/merge-k-sorted-lists/description/ 博主Github:https://github.com/GDUT-Rp/LeetCode 题目: 给你一个链表数组…...

[国产MCU]-W801开发实例-TCP客户端
TCP客户端 文章目录 TCP客户端1、TCP协议简单介绍2、W801创建TCP客户流程本文将详细介绍如何在W801中使用TCP客户端。 1、TCP协议简单介绍 传输控制协议 (TCP) 是一种标准,它定义了如何建立和维护应用程序可以用来交换数据的网络对话。 TCP 与 Internet 协议 (IP) 一起工作,…...
《爵士乐史》乔德.泰亚 笔记
第一章 【美国音乐的非洲化】 【乡村布鲁斯和经典布鲁斯】 布鲁斯:不止包括忧愁、哀痛 十二小节布鲁斯特征: 1.乐型(A:主、B:属、C/D:下属):A→A→B→A→C→D→A→A 2.旋律:大三、小三、降七、降五 盲人…...

工程制造领域:企业IT架构
一、IT组织规划架构图 1.1 IT服务保证梯队与指导思想 二、整体业务规划架构图 三、数据化项目规划架构图 四、应用系统集成架构图...

PY32F003F18点灯
延时函数学习完之后,可以学习PY32F003F18的GPIO输出功能。 1、Debug引脚默认被置于复用功能上拉或下拉模式:PA14默认为SWCLK: 置于下拉模式PA13默认为SWDIO: 置于上拉模式PF4默认为Boot:Boot引脚默认置于输入下拉模式 2、GPIO输出状态&#…...
Mac不想用iTerm2了怎么办
这东西真是让人又爱又恨,爱的是它的UI还真不错,恨的是它把我的环境给破坏啦!让我每次启动终端之后都要重新source激活我的python环境,而且虚拟环境前面没有括号啦!这怎么能忍!在UI和实用性面前我断然选择实…...

x86_64 ansible 源码编译安装
源码 GitHub - ansible/ansible: Ansible is a radically simple IT automation platform that makes your applications and systems easier to deploy and maintain. Automate everything from code deployment to network configuration to cloud management, in a languag…...

数据结构学习系列之顺序表的两种插入方式
方式1:在顺序表末端插入数据元素,代码如下:示例代码: int insert_seq_list_1(list_t *seq_list,int data){if(NULL seq_list){printf("入参为NULL\n");return -1;}if(N seq_list->count){printf("顺序表已满…...
)
Matlab/Python教程系列 | 根据目录下的已有图片制作视频(动画)
MATLAB和Python的编程教程: 根据目录下的已有图片制作视频(动画) 注1:本文系“MATLAB/Python编程教程”系列之一,致力于使用Python和Matlab实现特定的功能。本次要实现的功能是:根据目录下的已有图片制作视频(动画)。 在这个教程中,我们将一起学习如何使用MATLAB和Python编…...
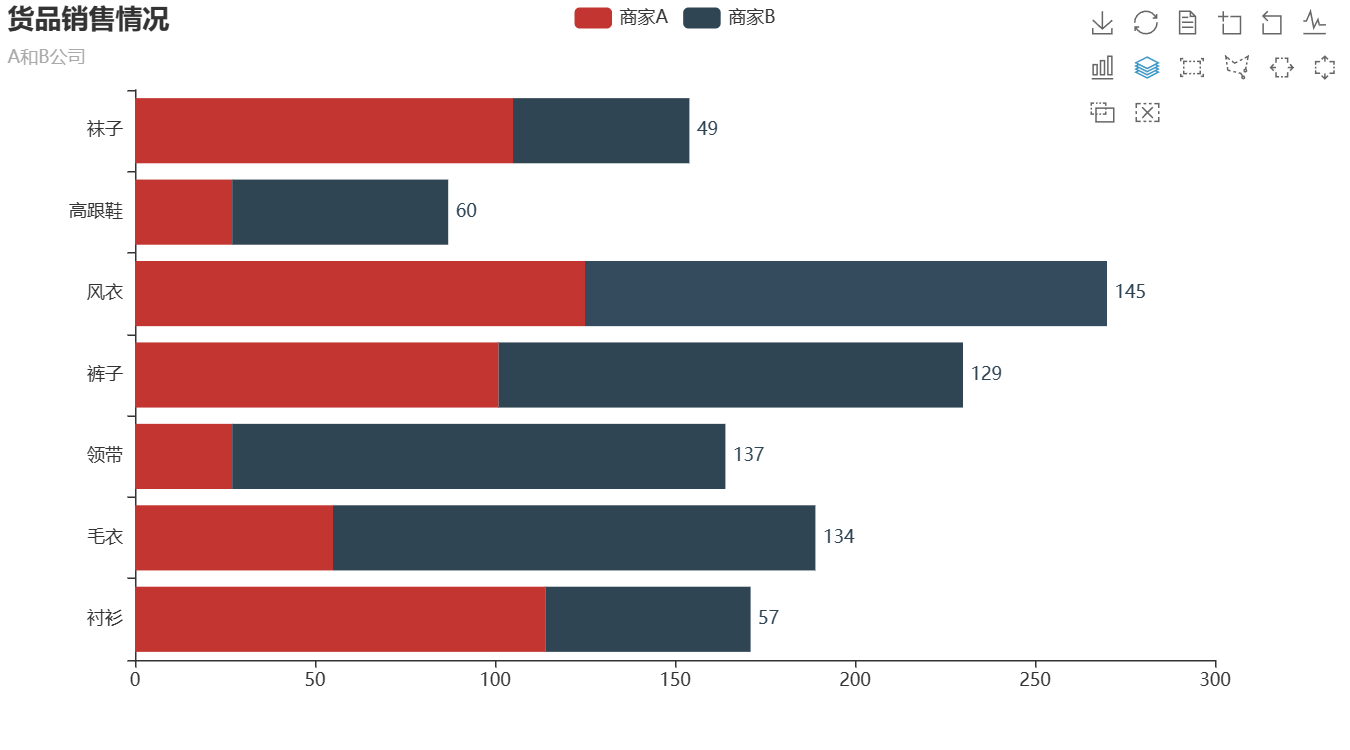
Pyecharts数据可视化(一)
目录 1.Pyecharts简介 2.Pyecharts的常用方法 3.Pyecharts绘制柱状图 3.1 绘制并列柱状图 3.2 绘制水平直方图 1.Pyecharts简介 Pyecharts是一个用于创建交互式图表的Python库。它基于Echarts,一个强大的JavaScript图表库,Pyecharts允许Python开发者…...

stable diffusion实践操作-提示词-图片结构
系列文章目录 stable diffusion实践操作-提示词 文章目录 系列文章目录前言一、提示词汇总1.1 图片结构11.2 图片结构21.3 图片结构3 二、总结 前言 本文主要收纳总结了提示词-图片结构。 一、提示词汇总 1.1 图片结构1 StylesArtistshudson river school哈得逊河学派alpho…...

程序员自由创业周记#2:前期准备
感恩 上次公开了创业的决定后,得到了很多亲朋好友和陌生朋友的鼓励或支持,以不同的形式,感动之情溢于言表。这些都会记在心里,大恩不言谢~ 创业方向 笔者是一名资质平平的iOS开发程序猿,创业项目也就是开发App卖&am…...
:Springboot实现Elasticsearch指标聚合与下钻分析open-API)
Elasticsearch实战(四):Springboot实现Elasticsearch指标聚合与下钻分析open-API
文章目录 系列文章索引一、指标聚合与分类1、什么是指标聚合(Metric)2、Metric聚合分析分为单值分析和多值分析两类3、概述 二、单值分析API设计1、Avg(平均值)(1)对所有文档进行avg聚合(DSL)(2…...
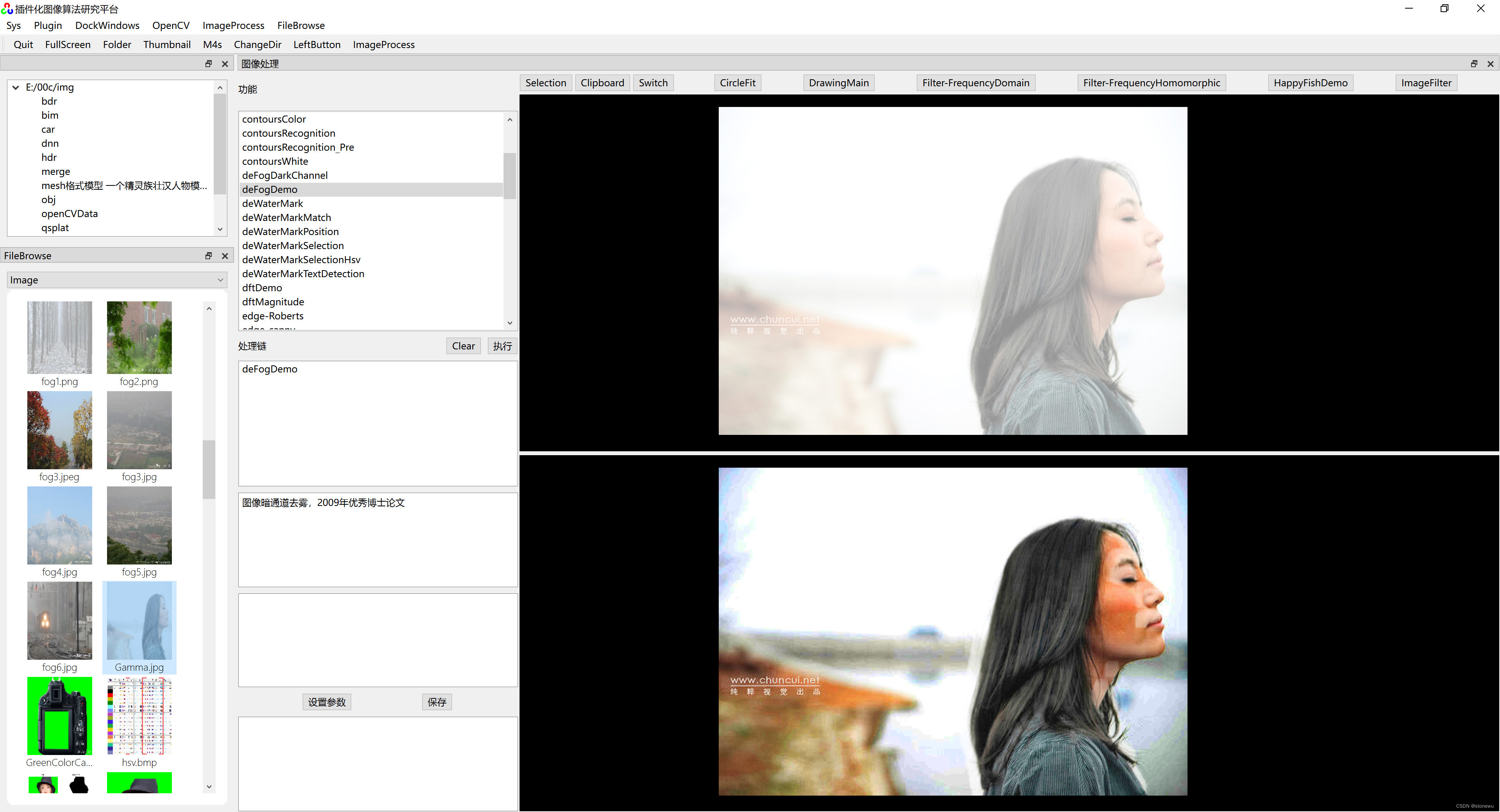
Opencv图像暗通道调优
基于雾天退化模型的去雾算法,Opencv图像暗通道调优,(清华版代码)对普通相片也有较好的调优效果,相片更通透。 结合代码实际运行效果、算法理论模型、实际代码。我个人理解,实际效果是对图像的三个颜色通道…...

怎样来实现流量削峰方案
削峰从本质上来说就是更多地延缓用户请求,以及层层过滤用户的访问需求,遵从“最后落地到数据库的请求数要尽量少”的原则。 1.消息队列解决削峰 要对流量进行削峰,最容易想到的解决方案就是用消息队列来缓冲瞬时流量,把同步的直…...

git status搜索.c和.h后缀及git新建分支
git status搜索.c和.h后缀及git新建分支 1.脚本代码2.git新建分支(1)创建新分支(2)删除本地分支(3)删除远端分支(4)合并分支3.指定历史版本创建分支1.脚本代码 $ git status | grep "\.[hc]$"$ 是行尾的意思 \b 就是用在你匹配整个单词的时候。 如果不是整个…...

【配置环境】Visual Studio 配置 OpenCV
目录 一,环境 二,下载和配置 OpenCV 三,创建一个 Visual Studio 项目 四,配置 Visual Studio 项目 五,编写并编译 OpenCV 程序 六,解决CMake编译OpenCV报的错误 一,环境 Windows 11 家庭中…...
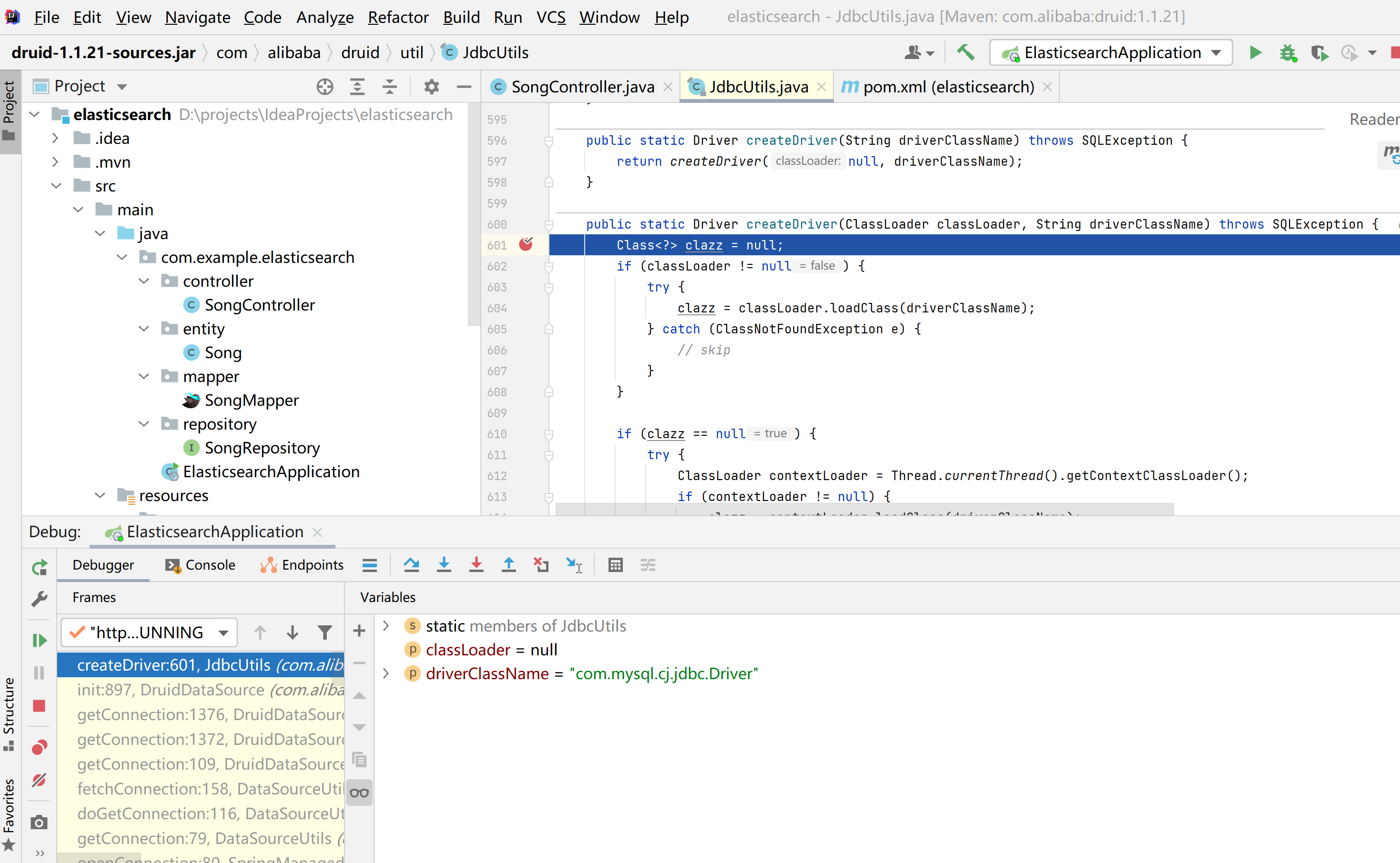
java.sql.SQLException: com.mysql.cj.jdbc.Driver
这篇文章分享一下Springboot整合Elasticsearch时遇到的一个问题,项目正常启动,但是查询数据库的时候发生了一个异常java.sql.SQLException: com.mysql.cj.jdbc.Driver java.sql.SQLException: com.mysql.cj.jdbc.Driverat com.alibaba.druid.util.JdbcU…...
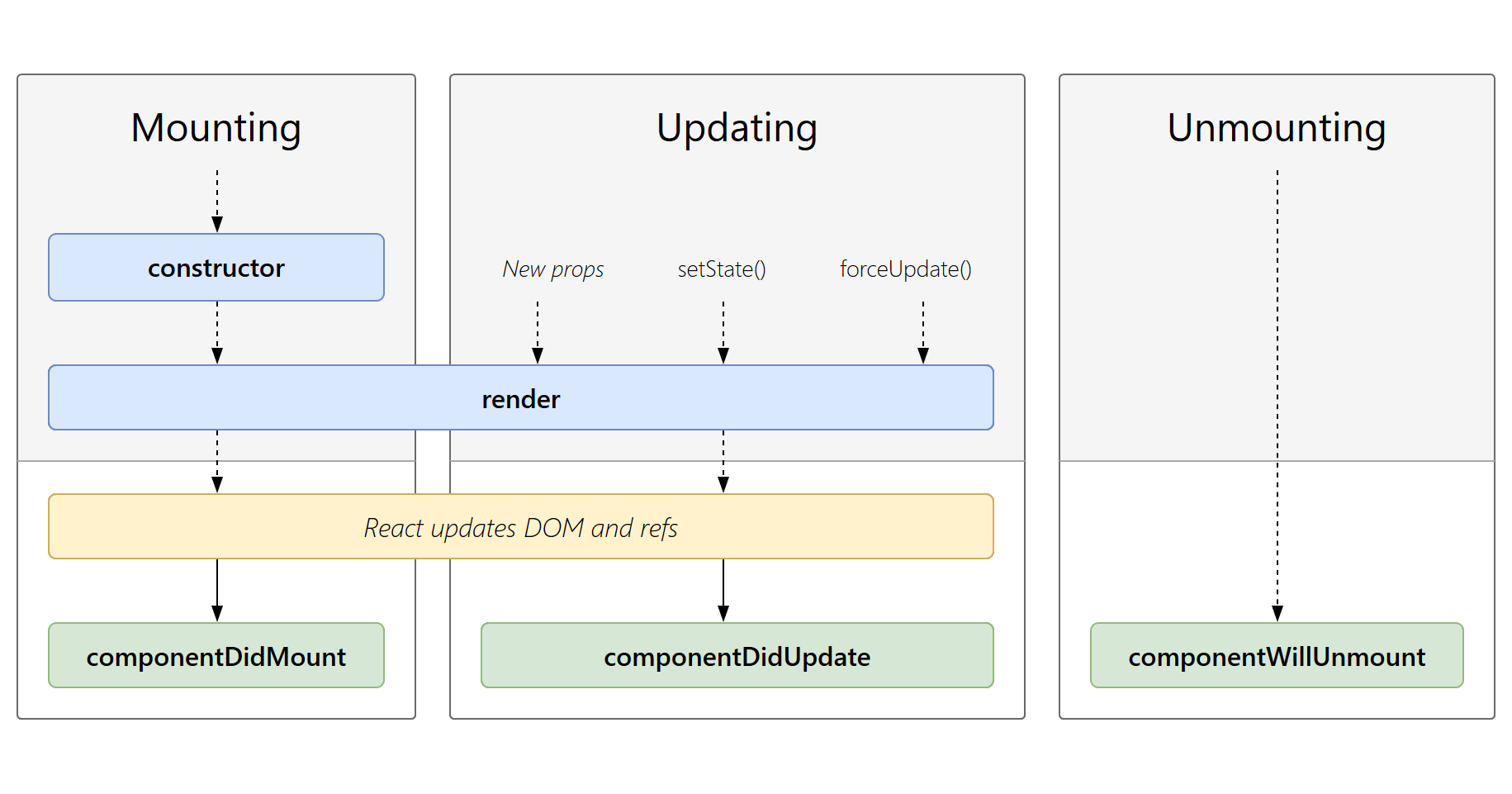
React笔记(四)类组件(2)
一、类组件的props属性 组件中的数据,除了组件内部的状态使用state之外,状态也可以来自组件的外部,外部的状态使用类组件实例上另外一个属性来表示props 1、基本的使用 在components下创建UserInfo组件 import React, { Component } from…...

点云从入门到精通技术详解100篇-点云信息编码
目录 前言 研究发展现状 点云几何信息压缩 点云属性信息压缩 点云压缩算法的相关技术...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
