Ajax与jQuery
目录
Ajax是一种异步无刷新的技术
Ajax的优点:
- 可以无需刷新页面与服务器端进行通信
- 允许根据用户事件来更新部分页面内容
Ajax的缺点:
- 没有浏览历史,不能回退
- 存在跨域问题(同源)
- SEO(搜索引擎优化)不友好
jquery 调用 ajax 方法:
$.ajax
格式:
$.ajax({ [参数] });
格式: $.ajax(});参数:
type: 请求方式GET/POSTurl: 请求地址url
async: 是否异步,默认是true表示异步
data: 发送到服务器的数据
dataType: 预期服务器返回的数据类型
contentType: 设置请求头
success: 请求成功时调用此函数
error: 请求失败时调用此函数
$.get
这是一个简单的GET 请求功能以取代复杂 $ajax
请求成功时可调用回调函数。如果需要在出错时执行函数,请使用 $.ajax。
语法:
// 1.请求json文件,忽略返回值
$.get( 'js/cuisine_area.json' );
// 2.请求json文件,传递参数,忽略返回值
$.get( 'js/cuisine_area.json',{ name:"tom" ,age:100} );
// 3.请求json文件,拿到返回值,请求成功后可拿到返回值
$.get( 'js/cuisine_area.json',function( data ) {
console.log(data)
});
// 4.请求json文件,传递参数,拿到返回值
$.get('js/cuisine_area.json' , { name:"tom",age:100},function(data){
console.log(data) ;
});
$.post
$.getJSON
表示请求返回的数据类型是]SON格式的ajax请求
$.getJSON('js/cuisine_area.json' , { name:"tom",age:100},function(data){
console.log(data) ; //要求返回的数据类型时JSON格式
});
相关文章:

Ajax与jQuery
目录 Ajax是一种异步无刷新的技术 Ajax的优点: 可以无需刷新页面与服务器端进行通信允许根据用户事件来更新部分页面内容 Ajax的缺点: 没有浏览历史,不能回退存在跨域问题(同源)SEO(搜索引擎优化&#x…...
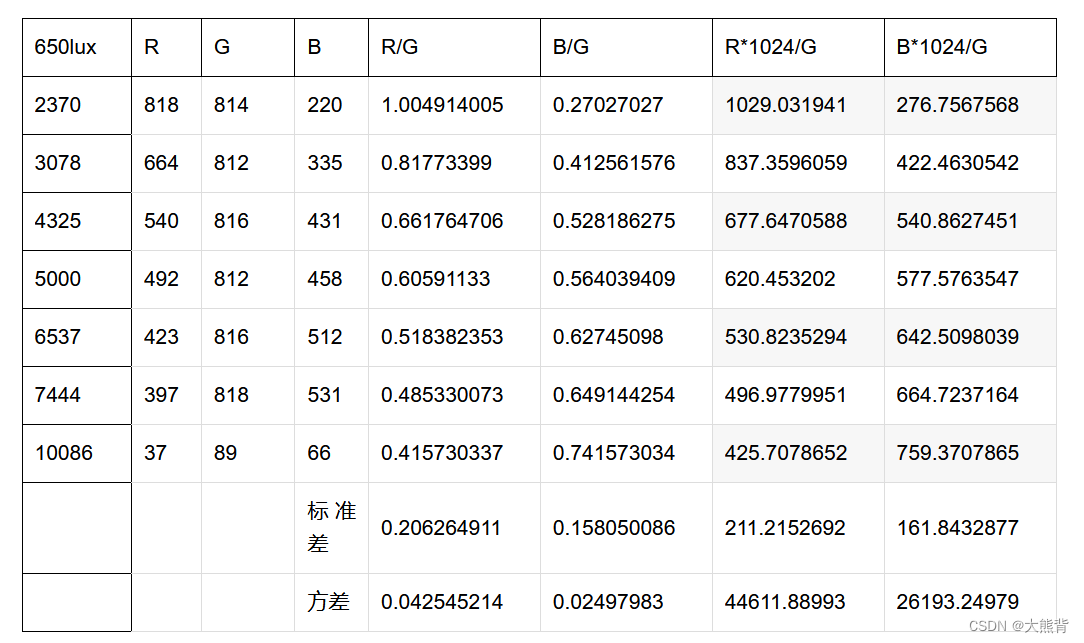
色温曲线坐标轴的选取:G/R、G/B还是R/G、B/G ?
海思色温曲线坐标 Mstar色温曲线坐标 高通色温曲线坐标 联咏色温曲线坐标 查看各家白平衡调试界面,比如海思、Mstart、高通等调试资料,白平衡模块都是以R/G B/G作为坐标系的两个坐标轴,也有方案是以G/R G/B作为坐标系的两个坐标轴。 以G/R G…...

maven部署
一、下载Maven 地址:Maven – Download Apache Maven 二、解压缩,设置环境变量 tar -xvf apache-maven-3.8.8-bin.tar.gz export MAVEN_HOME/opt/apache-maven-3.8.8 export PATH$MAVEN_HOME/bin:$PATH echo $MAVEN_HOME echo $PATH mvn -v...

docker进阶作业
一、使用mysql:5.6和 owncloud 镜像,构建一个个人网盘。 安装Docker:确保已在CentOS 7.5上安装了Docker。 拉取MySQL 5.6镜像:使用以下命令从Docker Hub上拉取MySQL 5.6镜像。 docker pull mysql:5.6 运行MySQL容器:使用以下命令…...
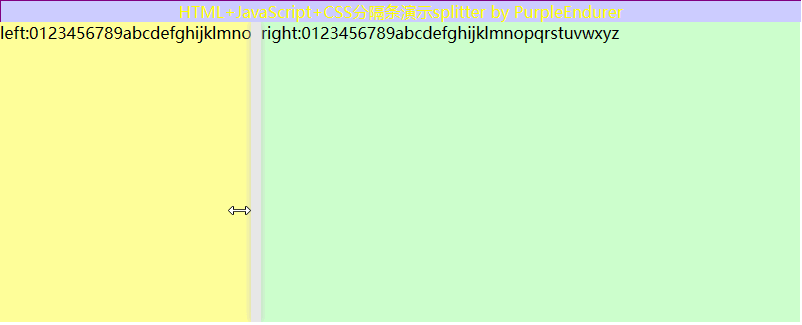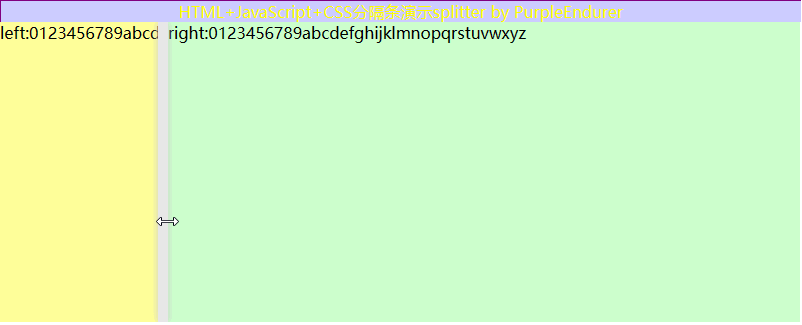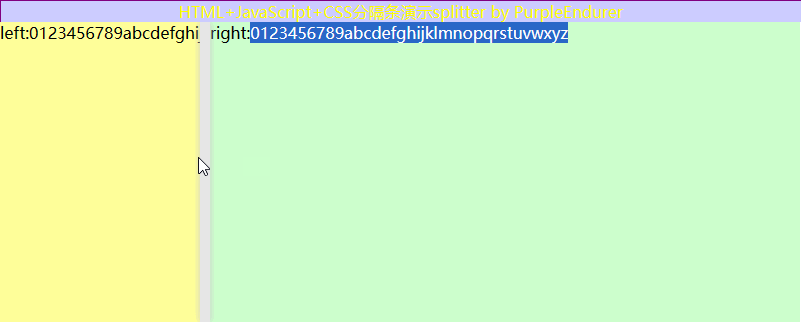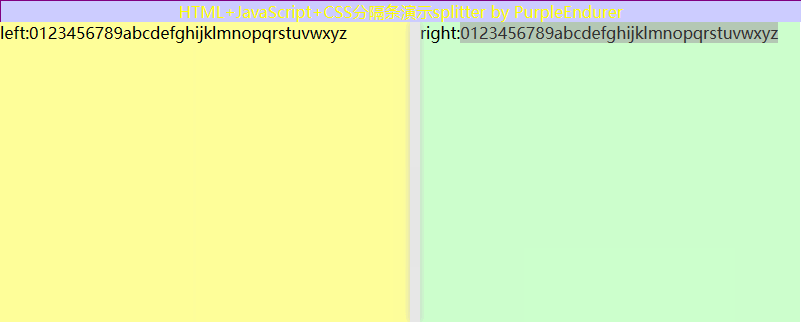
HTML+JavaScript+CSS DIY 分隔条splitter
一、需求分析 现在电脑的屏幕越来越大,为了利用好宽屏,我们在设计系统UI时喜欢在左侧放个菜单或选项面板,在右边显示与菜单或选项对应的内容,两者之间用分隔条splitter来间隔,并可以通过拖动分隔条splitter来动态调研…...

Oracle-day5:新增、复制建表、表结构、表数据、删除
目录 一、insert新增数据 二、复制建表 三、表结构修改 四、查看表结构、表数据处理 五、修改表数据 六、删除语句 八、练习题 一、insert新增数据 /* ---------- 一、DML 数据操作语言-------- -- 1、增加数据 insert 语法:insert into 表名 (列1,列2,…...
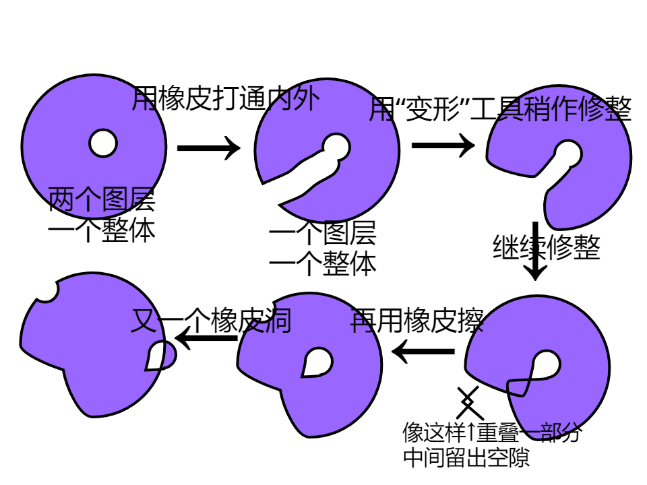
Scratch 画画的技巧
前言 美术是一种艺术,且不局限于纸张,就像电脑绘图也属于美术。我至今已有三年多的画龄,经验丰富,尤其擅长在scratch造型编辑器上画矢量图。今天给大家分享一些实用的技巧。 1.讲解 用橡皮工具给一个圆擦出“橡皮洞” 橡皮工具&a…...

国际版阿里云/腾讯云:阿里弹性云手机正式公测
阿里弹性云手机正式公测 什么是“云手机”?与我们传统的手机有何区别?它又有什么用处呢?当你接触到云手机概念的时候,是不是也会有这一连串的疑问。本文将为你揭开云手机的奥秘面纱。 2021年12月1日,阿里弹性云手机正…...
服务器数据恢复- RAID5出现故障后恢复数据和操作系统的案例
服务器数据恢复环境: 某品牌服务器中有4块SAS硬盘组建了一组RAID5阵列,另外1块磁盘作为热备盘使用。上层操作系统为redhat linux,部署了一个数据库是oracle的OA。 服务器故障&初检: RAID5中一块磁盘离线后热备盘未自动激活re…...

Vue3实现可视化拖拽标签小程序
介绍 实现功能:可视化标签拖拽,双击标签可修改标签内容 HTML结构 <div class"box" v-move><div class"header">标签1</div><div dblclick"startEditing" v-if"!isEditing">{{content…...

SSM 前端使用AJAX方式,fromdata文件格式上传二进制流文件
今天在上课的时候,遇到了一个比较坑的问题,有个学生拿来了她的代码,让我给她看看为什么传值传不过来。 首先,前端是这样的: function upload(){var formData new FormData();formData.append(images, $(#previewImg)…...

LeetCode-455-分发饼干-贪心算法
题目描述: 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 jÿ…...

新版 Next.js 从入门到入土
本教程用的Next.js 是 13 版本 Next.js 简介 完善的React项目,搭建轻松自带数据同步,解决服务端渲染最大难点丰富的插件灵活配置 创建第一个项目 手动创建 初始化 npm init安装所需要的依赖包 npm install --save react react-don next增加快捷命…...

OpenCV(十):图像缩放、翻转、拼接的介绍与使用
目录 (1)图像缩放:resize() (2)图像翻转: flip() (3)图像拼接:hconcat() 和vconcat() (1)图像缩放:resize() 使用 cv2.resize() 函…...

C++ 学习之 构造函数 和 析构函数
前言 总的来说,构造函数负责对象的初始化,而析构函数负责对象的清理和资源释放。它们是C面向对象编程中非常重要的概念,用于管理对象的生命周期,确保对象在创建和销毁时都能够正确地进行初始化和清理。 正文 看代码 class perso…...

加快 MySQL 数据迁移
目录 一、先导 1. 自建目标实例 2. 配置目标主从 二、源导出 1. 生成查询用户权限的SQL语句 2. 生成权限的SQL语句 3. 生成创建非主键索引的SQL语句 4. 导出源库结构 5. 导出源库数据 三、目标导入 1. 目标实例设置 2. 创建用户与权限 3. 处理结构导出文件 4. 导…...

CANalyzer panel
(1205条消息) CAPL 脚本中对信号,系统变量,环境变量的 事件响应_capl programs脚本怎么写信号运算_蚂蚁小兵的博客-CSDN博客 注意环境变量是在工程关联的dbc中创建的;而系统变量是在CANoe工程工具栏的”Environment”下的”System Variables”…...
延迟队列的理解与使用
目录 一、场景引入 二、延迟队列的三种场景 1、死信队列TTL对队列进行延迟 2、创建通用延时消息死信队列 对消息延迟 3、使用rabbitmq的延时队列插件 x-delayed-message使用 父pom文件 pom文件 配置文件 config 生产者 消费者 结果 一、场景引入 我们知道可以通过TT…...

jQuery成功之路——jQuery的DOM操作简单易懂
jQuery的DOM操作 1.jQuery操作内容 jQuery操作内容 1. text() 获取或修改文本内容 类似于 dom.innerText 2. html() 获取或修改html内容 类似 dom.innerHTML 注意: 1. text() 是获取设置所有 2. html() 是获取第一个,设置所有 <!DOCTYPE html> <html lang"zh…...

C++ 学习系列 -- 智能指针 make_shared 与 make_unique
一 make_shared 1.1 make_shared 是什么? c 11 中 引入了智能指针 shared_ptr,以及一个模板函数 make_shared 来生成一个制定类型的 shared_ptr。 1.2 引入 make_shared ,解决了什么问题? make_shared的引入,主…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
