数学建模:Logistic回归预测
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛
数学建模:Logistic回归预测
Logistic回归预测
logistic方程的定义:
x t = 1 c + a e b t x_{t}=\frac{1}{c+ae^{bt}}\quad xt=c+aebt1
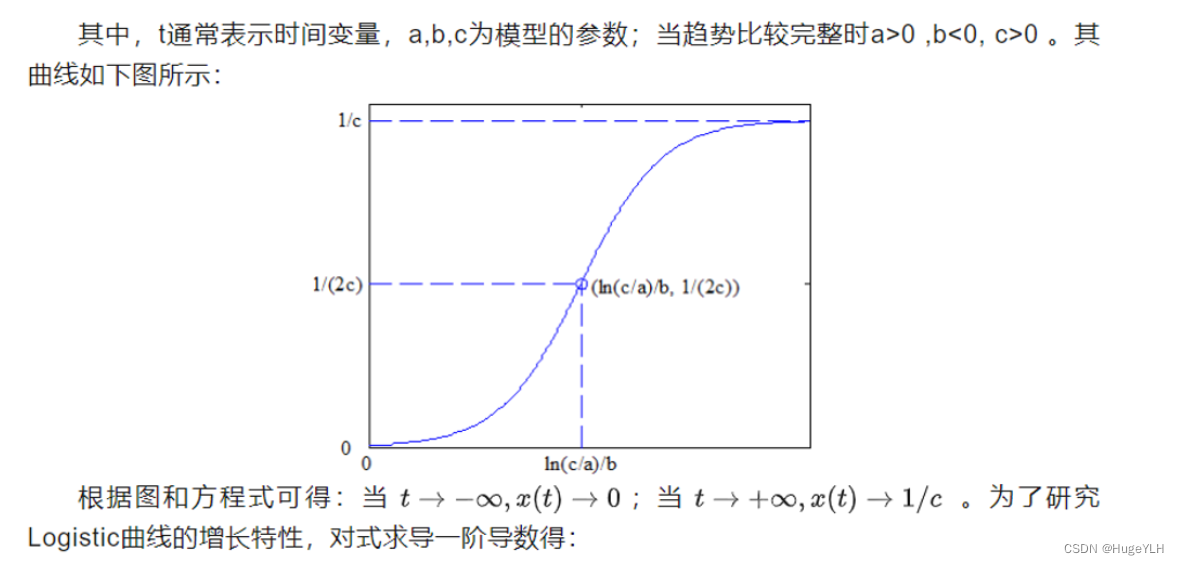
d x d t = − a b e b t ( c + a e b t ) 2 > 0 \frac{dx}{dt}=\frac{-abe^{bt}}{\left(c+ae^{bt}\right)^2}>0 dtdx=(c+aebt)2−abebt>0
算法流程
-
建立logistic方程
-
求解 其三个未知系数:
a,b,c -
Yule算法求解:构建如下的 线性方程 Z Z Z
x t + 1 − x t x t + 1 = 1 − x t x t + 1 = 1 − c + a e b ( t + 1 ) c + a e b t = ( a e b t + c − c ) ( 1 − e b ) ( c + a e b t ) = ( 1 − e b ) − c ( 1 − e b ) x t \begin{aligned}\frac{x_{t+1}-x_{t}}{x_{t+1}}=1-\frac{x_{t}}{x_{t+1}} \\&=1-\frac{c+ae^{b(t+1)}}{c+ae^{bt}} \\&=\frac{\left(ae^{bt}+c-c\right)\left(1-e^b\right)}{\left(c+ae^{bt}\right)} \\&=\left(1-e^b\right)-c\left(1-e^b\right)x_t\quad\end{aligned} xt+1xt+1−xt=1−xt+1xt=1−c+aebtc+aeb(t+1)=(c+aebt)(aebt+c−c)(1−eb)=(1−eb)−c(1−eb)xt
-
对此方程进行最小二乘法(OLS),得到方程的估计值,然后进而得到 a,b,c的值:
γ = 1 − e b 以及 β = − c ( 1 − e b ) , \gamma=1-e^b\text{ 以及 }\beta=-c\big(1-e^b\big), γ=1−eb 以及 β=−c(1−eb),
a ^ = e x p { 1 n [ ∑ t = 1 n l n ( 1 x t − c ^ − n ( n + 1 ) 2 b ^ ) ] } 5 ) \hat a=exp\bigg\{\frac{1}{n}\bigg[\sum_{t=1}^nln(\frac{1}{x_t}-\hat c-\frac{n(n+1)}{2}\hat b)\bigg]\bigg\}5) a^=exp{n1[t=1∑nln(xt1−c^−2n(n+1)b^)]}5)
- 然后需要预测自变量值 x x x 直接带入即可。
代码实现
function [a,b,c] = mfunc_Logistic(X)% logistic 回归预测% params:% X: 输入向量% returns:% a,b,c: 分别为logistic的未知参数n=length(X)-1;% 得到线性方程: Zfor t=1:nZ(t)=(X(t+1)-X(t))/X(t+1);end% 前面插一列全1向量X1=[ones(n,1) X(1:n)']; % (46,2)% 对线性方程 Z 进行最小二乘法OLS% B:回归系数% bint:回归系数的置信区间% r:残差% rint:残差的置信区间% stats:包含四个统计量:R^2, F, 概率p, 估计误差方差Y=Z';[B,Bint,r,rint,stats]=regress(Y,X1);%最小二乘(OLS)gamma=B(1,1);beta=B(2,1);%% 带入公式 计算logistic方程的 abcb=log(1-gamma);c=beta/(exp(b)-1);a=exp((sum(log(1./X(1:n)-c))-n*(n+1)*b/2)/n);
end
相关文章:

数学建模:Logistic回归预测
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:Logistic回归预测 Logistic回归预测 logistic方程的定义: x t 1 c a e b t x_{t}\frac{1}{cae^{bt}}\quad xtcaebt1 d x d t − a b e b t ( c a e b t ) 2 >…...

一个面向MCU的小型前后台系统
JxOS简介 JxOS面向MCU的小型前后台系统,提供消息、事件等服务,以及软件定时器,低功耗管理,按键,led等常用功能模块。 gitee仓库地址为(复制到浏览器打开): https://gitee.com/jer…...
软件外包开发人员分类
在软件开发中,通常会分为前端开发和后端开发,下面和大家分享软件开发中的前端开发和后端开发分类和各自的职责,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作。 1. 前端开发&…...

HTML 元素被定义为块级元素或内联元素
大多数 HTML 元素被定义为块级元素或内联元素。 10. 块级元素 块级元素在浏览器显示时,通常会以新行来开始(和结束)。 我们已经学习过的块级元素有: <h1>, <p>, <ul>, <table> 等。 值得注意的是: <p> 标签…...

单调递增的数字【贪心算法】
单调递增的数字 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 public class Solution {public int monotoneIncreasingDigits…...
gnuradio-hackrf_info.exe -FM频率使用
97910000...
--生产环境的线程问题诊断)
JVM学习(三)--生产环境的线程问题诊断
1.如何定位哪个进程对cpu占用过高 使用top命令 2.如何定位到某个进程的具体某个线程 使用ps H -eo pid,tid,%cpu | grep 进程id (可以具体定位到某个进程的某个线程的cpu占用情况) 3.如何查看有问题线程的具体信息,定位到代码的行数 使用jstack 进程id 可以找…...

PHP数组处理$arr1转换为$arr2
请编写一段程序将$arr1转换为$arr2 $arr1 array( 0>array (fid>1,tid>1,name>Name1), 1>array (fid>2,tid>2,name>Name2), 2>array (fid>3,tid>5,name>Name3), 3>array (fid>4,tid>7,name>Name4), 4>array (fid>5,tid…...
安全通告 TFV-10 (CVE-2022-47630))
ATF(TF-A)安全通告 TFV-10 (CVE-2022-47630)
安全之安全(security)博客目录导读 ATF(TF-A)安全通告汇总 目录 一、ATF(TF-A)安全通告 TFV-10 (CVE-2022-47630) 二、CVE-2022-47630 2.1 Bug 1:证书校验不足 2.2 Bug 2:auth_nvctr()中缺少边界检查...

详解 SpringMVC 中获取请求参数
文章目录 1、通过ServletAPI获取2、通过控制器方法的形参获取请求参数3、[RequestParam ](/RequestParam )4、[RequestHeader ](/RequestHeader )5、[CookieValue ](/CookieValue )6、通过POJO获取请求参数7、解决获取请求参数的乱码问题总结 在Spring MVC中,获取请…...

Message: ‘chromedriver‘ executable may have wrong permissions.
今天运行项目遇到如下代码 driverwebdriver.Chrome(chrome_driver, chrome_optionsoptions)上述代码运行报错如下: Message: chromedriver executable may have wrong permissions. Please see https://sites.google.com/a/chromium.org/chromedriver/home出错的原…...
每日一题 1372二叉树中的最长交错路径
题目 给你一棵以 root 为根的二叉树,二叉树中的交错路径定义如下: 选择二叉树中 任意 节点和一个方向(左或者右)。如果前进方向为右,那么移动到当前节点的的右子节点,否则移动到它的左子节点。改变前进方…...

【力扣每日一题】2023.9.2 最多可以摧毁的敌人城堡数量
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题难在阅读理解,题目看得我匪夷所思,错了好多个测试用例才明白题目说的是什么。 我简单翻译一下就是寻找1和…...

kotlin实现java的单例模式
代码 package com.flannery.interviewdemo.singleinstance//https://blog.csdn.net/Jason_Lee155/article/details/128796742 Java实现 //public class SingletonDemo { // private static SingletonDemo instancenew SingletonDemo(); // private SingletonDemo() // …...

使用 KeyValueDiffers 检测Angular 对象的变化
使用 KeyValueDiffers 检测Angular 对象的变化 ngDoCheck钩子 ngDoCheck 是 Angular 生命周期钩子之一。它允许组件在 Angular 检测到变化时执行自定义的变化检测逻辑。 当任何组件或指令的输入属性发生变化、在组件内部发生了变更检测周期或者当主动触发变更检测策略&#…...

Macos 10.13.2安装eclipse
eclipse for php 安装2021-12最后版本4.22 2021-12 R | Eclipse Packages jdk17 x64 dmg安装包,要安装jdk这个才能运行 Java Downloads | Oracle...
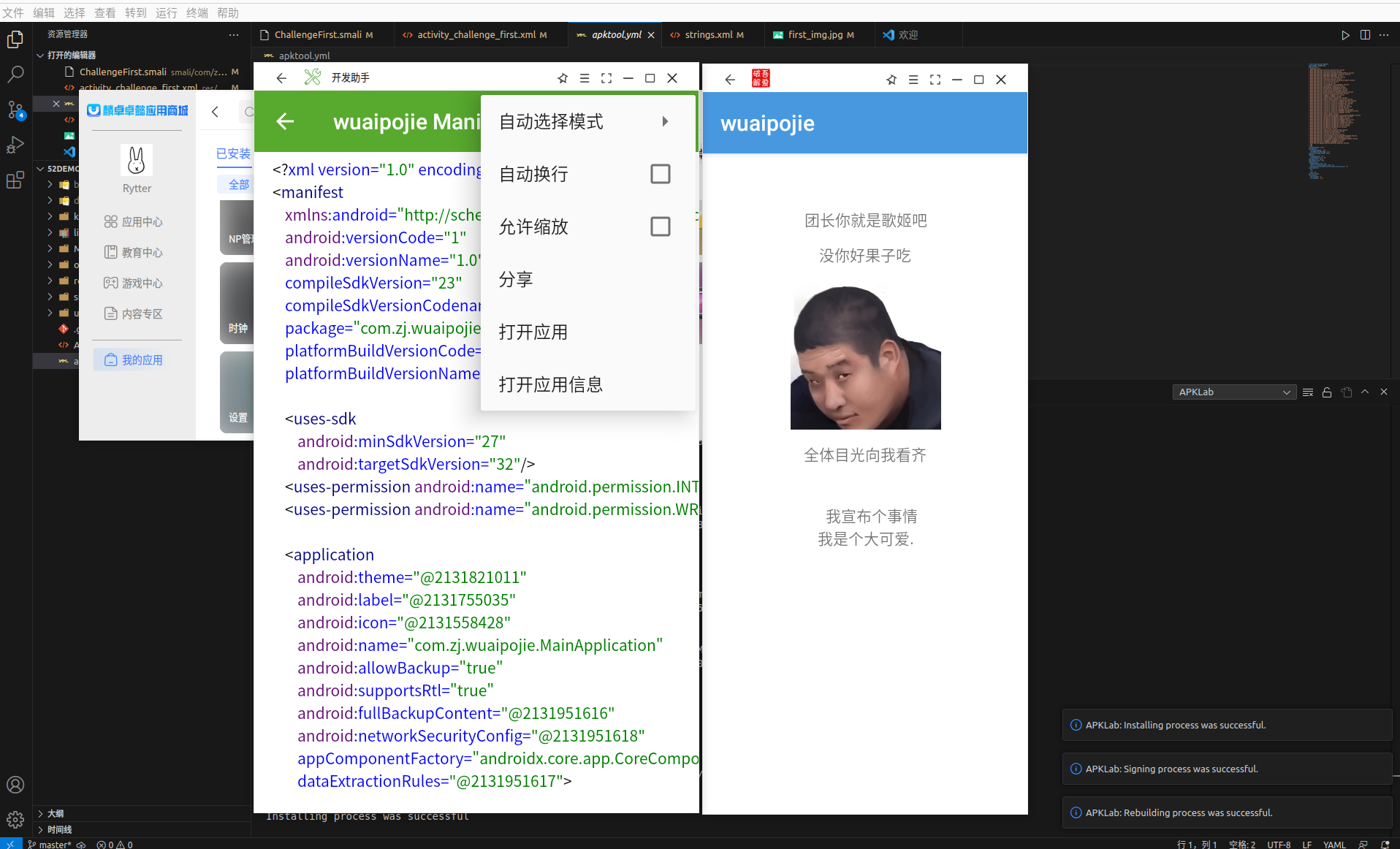
Android逆向学习(一)vscode进行android逆向修改并重新打包
Android逆向学习(一)vscode进行android逆向修改并重新打包 写在前面 其实我不知道这个文章能不能写下去,其实我已经开了很多坑但是都没填上,现在专利也发出去了,就开始填坑了,本坑的主要内容是关于androi…...

【深入浅出设计模式--状态模式】
深入浅出设计模式--状态模式 一、背景二、问题三、解决方案四、 适用场景总结五、后记 一、背景 状态模式是一种行为设计模式,让你能在一个对象的内部状态变化时改变其行为,使其看上去就像改变了自身所属的类一样。其与有限状态机的概念紧密相关&#x…...

Debezium系列之:Debezium Server在生产环境大规模应用详细的技术方案
Debezium系列之:Debezium Server在生产环境大规模应用详细的技术方案 一、需求背景二、Debezium Server实现技术三、技术方案流程四、生成接入配置五、新增数据库接入和删除数据库接入效果六、监控zookeeper节点程序七、新增数据库接入部署debezium server程序八、删除数据库接…...

Echart笔记
Echart笔记 柱状图带背景色的柱状图将X与Y轴交换制作为进度条 柱状图 带背景色的柱状图 将X与Y轴交换制作为进度条 //将X与Y轴交换制作为进度条 option { xAxis: {type: value,min:0,max:100,show:false,//隐藏x轴},yAxis: {type: category,data:[进度条],show:false,//隐…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...

break 语句和 continue 语句
break语句和continue语句都具有跳转作用,可以让代码不按既有的顺序执行 break break语句用于跳出代码块或循环 1 2 3 4 5 6 for (var i 0; i < 5; i) { if (i 3){ break; } console.log(i); } continue continue语句用于立即终…...

ubuntu清理垃圾
windows和ubuntu 双系统,ubuntu 150GB,开发用,基本不装太多软件。但是磁盘基本用完。 1、查看home目录 sudo du -h -d 1 $HOME | grep -v K 上面的命令查看$HOME一级目录大小,发现 .cache 有26GB,.local 有几个GB&am…...
