HTML 元素被定义为块级元素或内联元素
大多数 HTML 元素被定义为块级元素或内联元素。
10. 块级元素
块级元素在浏览器显示时,通常会以新行来开始(和结束)。
我们已经学习过的块级元素有: <h1>, <p>, <ul>, <table> 等。
值得注意的是:
<p>标签中不能包含任何块级元素。
<div> 元素
<div> 元素是块级元素,它可用于组合其他 HTML 元素的容器。
<div> 元素没有特定的含义。除此之外,由于它属于块级元素,浏览器会在其前后显示折行。
如果与 CSS 一同使用,<div> 元素可用于对大的内容块设置样式属性。
<div> 元素的另一个常见的用途是文档布局。
值得注意的是:
<div>取代了使用表格定义布局的老式方法。
内联元素
内联元素在显示时通常不会以新行开始。
我们已经学习过的内联元素有: <td>, <a>, <img> 等。
值得注意的是:
<a>标签中不能包含<a>标签,但可以包含其他任何元素。
<span> 元素
<span> 元素是内联元素,可用作文本的容器。<span> 元素也没有特定的含义。
当与 CSS 一同使用时,<span> 元素可用于为部分文本设置样式属性。
值得注意的是: 内联元素中不能包含块级元素。一般都是块级元素中包含内联元素。
undefined
相关文章:

HTML 元素被定义为块级元素或内联元素
大多数 HTML 元素被定义为块级元素或内联元素。 10. 块级元素 块级元素在浏览器显示时,通常会以新行来开始(和结束)。 我们已经学习过的块级元素有: <h1>, <p>, <ul>, <table> 等。 值得注意的是: <p> 标签…...

单调递增的数字【贪心算法】
单调递增的数字 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 public class Solution {public int monotoneIncreasingDigits…...
gnuradio-hackrf_info.exe -FM频率使用
97910000...
--生产环境的线程问题诊断)
JVM学习(三)--生产环境的线程问题诊断
1.如何定位哪个进程对cpu占用过高 使用top命令 2.如何定位到某个进程的具体某个线程 使用ps H -eo pid,tid,%cpu | grep 进程id (可以具体定位到某个进程的某个线程的cpu占用情况) 3.如何查看有问题线程的具体信息,定位到代码的行数 使用jstack 进程id 可以找…...

PHP数组处理$arr1转换为$arr2
请编写一段程序将$arr1转换为$arr2 $arr1 array( 0>array (fid>1,tid>1,name>Name1), 1>array (fid>2,tid>2,name>Name2), 2>array (fid>3,tid>5,name>Name3), 3>array (fid>4,tid>7,name>Name4), 4>array (fid>5,tid…...
安全通告 TFV-10 (CVE-2022-47630))
ATF(TF-A)安全通告 TFV-10 (CVE-2022-47630)
安全之安全(security)博客目录导读 ATF(TF-A)安全通告汇总 目录 一、ATF(TF-A)安全通告 TFV-10 (CVE-2022-47630) 二、CVE-2022-47630 2.1 Bug 1:证书校验不足 2.2 Bug 2:auth_nvctr()中缺少边界检查...

详解 SpringMVC 中获取请求参数
文章目录 1、通过ServletAPI获取2、通过控制器方法的形参获取请求参数3、[RequestParam ](/RequestParam )4、[RequestHeader ](/RequestHeader )5、[CookieValue ](/CookieValue )6、通过POJO获取请求参数7、解决获取请求参数的乱码问题总结 在Spring MVC中,获取请…...

Message: ‘chromedriver‘ executable may have wrong permissions.
今天运行项目遇到如下代码 driverwebdriver.Chrome(chrome_driver, chrome_optionsoptions)上述代码运行报错如下: Message: chromedriver executable may have wrong permissions. Please see https://sites.google.com/a/chromium.org/chromedriver/home出错的原…...
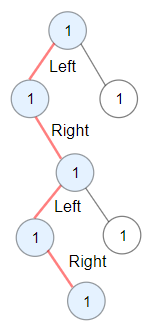
每日一题 1372二叉树中的最长交错路径
题目 给你一棵以 root 为根的二叉树,二叉树中的交错路径定义如下: 选择二叉树中 任意 节点和一个方向(左或者右)。如果前进方向为右,那么移动到当前节点的的右子节点,否则移动到它的左子节点。改变前进方…...

【力扣每日一题】2023.9.2 最多可以摧毁的敌人城堡数量
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题难在阅读理解,题目看得我匪夷所思,错了好多个测试用例才明白题目说的是什么。 我简单翻译一下就是寻找1和…...

kotlin实现java的单例模式
代码 package com.flannery.interviewdemo.singleinstance//https://blog.csdn.net/Jason_Lee155/article/details/128796742 Java实现 //public class SingletonDemo { // private static SingletonDemo instancenew SingletonDemo(); // private SingletonDemo() // …...

使用 KeyValueDiffers 检测Angular 对象的变化
使用 KeyValueDiffers 检测Angular 对象的变化 ngDoCheck钩子 ngDoCheck 是 Angular 生命周期钩子之一。它允许组件在 Angular 检测到变化时执行自定义的变化检测逻辑。 当任何组件或指令的输入属性发生变化、在组件内部发生了变更检测周期或者当主动触发变更检测策略&#…...

Macos 10.13.2安装eclipse
eclipse for php 安装2021-12最后版本4.22 2021-12 R | Eclipse Packages jdk17 x64 dmg安装包,要安装jdk这个才能运行 Java Downloads | Oracle...
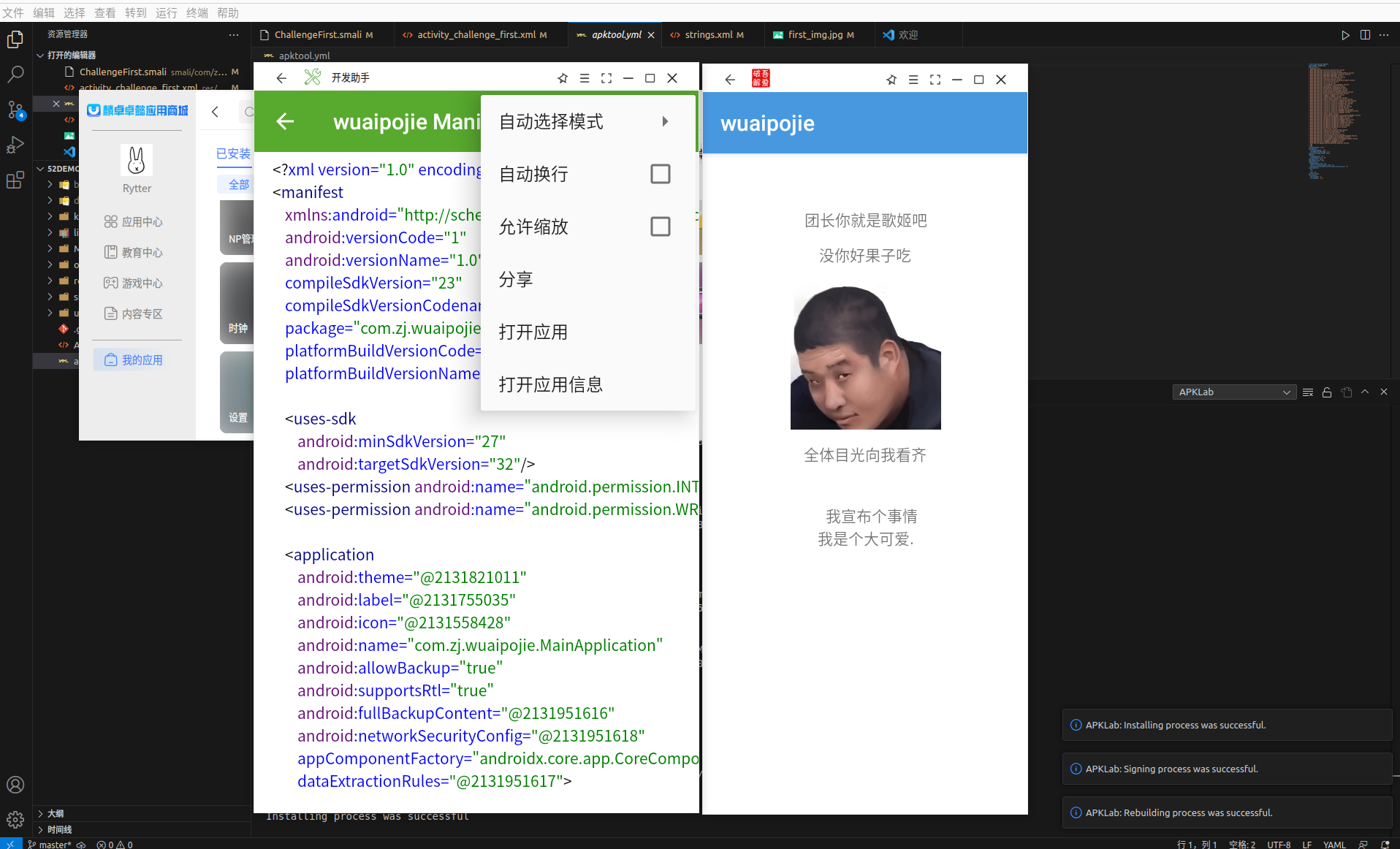
Android逆向学习(一)vscode进行android逆向修改并重新打包
Android逆向学习(一)vscode进行android逆向修改并重新打包 写在前面 其实我不知道这个文章能不能写下去,其实我已经开了很多坑但是都没填上,现在专利也发出去了,就开始填坑了,本坑的主要内容是关于androi…...

【深入浅出设计模式--状态模式】
深入浅出设计模式--状态模式 一、背景二、问题三、解决方案四、 适用场景总结五、后记 一、背景 状态模式是一种行为设计模式,让你能在一个对象的内部状态变化时改变其行为,使其看上去就像改变了自身所属的类一样。其与有限状态机的概念紧密相关&#x…...

Debezium系列之:Debezium Server在生产环境大规模应用详细的技术方案
Debezium系列之:Debezium Server在生产环境大规模应用详细的技术方案 一、需求背景二、Debezium Server实现技术三、技术方案流程四、生成接入配置五、新增数据库接入和删除数据库接入效果六、监控zookeeper节点程序七、新增数据库接入部署debezium server程序八、删除数据库接…...

Echart笔记
Echart笔记 柱状图带背景色的柱状图将X与Y轴交换制作为进度条 柱状图 带背景色的柱状图 将X与Y轴交换制作为进度条 //将X与Y轴交换制作为进度条 option { xAxis: {type: value,min:0,max:100,show:false,//隐藏x轴},yAxis: {type: category,data:[进度条],show:false,//隐…...
docker 笔记1
目录 1.为什么有docker ? 2.Docker 的核心概念 3.容器与虚拟机比较 3.1传统的虚拟化技术 3.2容器技术 3.3Docker容器的有什么作用? 3.4应用案例 4. docker 安装下载 4.1CentOS Docker 安装 4.2 Docker的基本组成 ?(面试)…...

HTTP Get 和 Post 的区别
分析&回答 使用规范 根据HTTP规范,GET用于信息获取,而且应该是安全的和幂等的。 根据HTTP规范,POST表示可能修改变服务器上的资源的请求。 传递参数 GET请求的数据会附在URL之后(就是把数据放置在HTTP协议头中)。…...

C++超级迷宫游戏
游戏效果 用钥匙、护盾等道具帮助你的小人通过大门、墙、怪物、岩浆等困难到达终点。 游戏代码 #include<bits/stdc.h> #include<conio.h> #include<windows.h> using namespace std; void Color(int a) {if(a0) SetConsoleTextAttribute(GetStdHandle(STD…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
