UVa11374 Airport Express(Dijkstra)
题意
给出经济路线以及商业路线,在给出起始点s,终止点e,在只能使用其中一个商业路线 的情况下输出最短路径
思路
如果选择商业路线为从u到v,则需要从s->u,u->v,v->e点的路径最短。使用Dijkstra计算出从s点到其它各点,以及从e点到其它各点的最短路径,然后遍历商业路线u,v,选取从s->u,u->v,v->e点中路线最短的
代码
#include <bits/stdc++.h>using namespace std;#define _for(i, a, b) for(int i = (a); i < (b); i++)
#define _rep(i, a, b) for (int i = (a); i <= (b); i++)struct Edge
{int u, v, d;
};struct HeapNode
{int u, d;bool operator<(const HeapNode& other) const{return d > other.d;}
};template <int SZV, int INF>
struct Dijkstra
{int n;vector<Edge> edges;vector<int> graph[SZV];bool done[SZV];int d[SZV], p[SZV];void init(int n){this->n = n;edges.clear();_for(i, 0, n) {graph[i].clear();}}void addEdge(int u, int v, int d){graph[u].push_back(edges.size());edges.push_back({u, v, d});}void dijkstra(int s){priority_queue<HeapNode> pq;fill_n(done, n, false);fill_n(d, n, INF);d[s] = 0;pq.push({s, 0});while (!pq.empty()) {HeapNode curNode = pq.top();pq.pop();int u = curNode.u;if (done[u]) {continue;}done[u] = true;_for(i, 0, graph[u].size()) {const auto& edge = edges[graph[u][i]];int v = edge.v;if (d[u] + edge.d < d[v]) {d[v] = d[u] + edge.d;p[v] = graph[u][i];pq.push({v, d[v]});}}}}void getPath(int s, int e, deque<int>& path, bool rev = false){int x = e;if (rev) {path.push_back(x);} else {path.push_front(x);}while (x != s) {x = edges[p[x]].u;if (rev) {path.push_back(x);} else {path.push_front(x);}}}
};void fastio()
{ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
}const int MAXN = 500 + 4;
const int INF = 1e9;int main()
{fastio();#ifndef ONLINE_JUDGEifstream fin("f:\\OJ\\uva_in.txt");streambuf* back = cin.rdbuf(fin.rdbuf());#endifint N, S, E;int kase = 0;while (cin >> N >> S >> E) {if (kase++) {cout << endl;}Dijkstra<MAXN, INF> sd, ed;sd.init(N + 1); ed.init(N + 1);int M;cin >> M;_for(i, 0, M) {int X, Y, Z;cin >> X >> Y >> Z;sd.addEdge(X, Y, Z);sd.addEdge(Y, X, Z);ed.addEdge(X, Y, Z);ed.addEdge(Y, X, Z);}sd.dijkstra(S);ed.dijkstra(E);int cu = -1;int ans = INF;deque<int> path;if (sd.d[E] < ans) {ans = sd.d[E];sd.getPath(S, E, path);}auto update = [&](int u, int v, int d) {if (sd.d[u] < ans && ed.d[v] < ans && sd.d[u] + d + ed.d[v] < ans) {ans = sd.d[u] + d + ed.d[v];cu = u;path.clear();sd.getPath(S, u, path);ed.getPath(E, v, path, true);}};int K;cin >> K;_for(i, 0, K) {int u, v, d;cin >> u >> v >> d;update(u, v, d);update(v, u, d);}_for(i, 0, path.size()) {if (i) {cout << " ";}cout << path[i];}cout << endl;if (cu == -1) {cout << "Ticket Not Used" << endl;} else {cout << cu << endl;}cout << ans << endl;}#ifndef ONLINE_JUDGEcin.rdbuf(back);#endifreturn 0;
}
相关文章:
)
UVa11374 Airport Express(Dijkstra)
题意 给出经济路线以及商业路线,在给出起始点s,终止点e,在只能使用其中一个商业路线 的情况下输出最短路径 思路 如果选择商业路线为从u到v,则需要从s->u,u->v,v->e点的路径最短。使用Dijkstra计算出从s点…...

hadoop的hdfs中避免因节点掉线产生网络风暴
hadoop的hdfs中避免因节点掉线产生网络风暴 控制节点掉线RPC风暴的参数 三个参数都是hdfs-site.xml中参数,具体可以参考apache hadoop官网,其实块的复制速度有两个方面决定,一是namenode分发任务的速度,二则是datanode之间进行复…...

2023年高教社杯 国赛数学建模思路 - 案例:最短时间生产计划安排
文章目录 0 赛题思路1 模型描述2 实例2.1 问题描述2.2 数学模型2.2.1 模型流程2.2.2 符号约定2.2.3 求解模型 2.3 相关代码2.4 模型求解结果 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 最短时…...
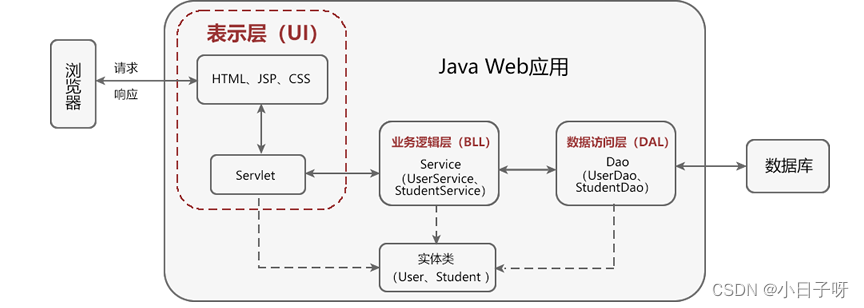
Spring MVC介绍
MVC模式是什么 MVC 模式,全称为 Model-View-Controller(模型-视图-控制器)模式,它是一种软件架构模式,其目标是将软件的用户界面(即前台页面)和业务逻辑分离,使代码具有更高的可扩展…...
5年测试在职经验之谈:2年功能测试、3年自动化测试,从入门到不可自拔...
毕业3年了,学的是环境工程专业,毕业后零基础转行做软件测试。 已近从事测试行业8年了,自己也从事过2年的手工测试,从事期间越来越觉得如果一直在手工测试的道路上前进,并不会有很大的发展,所以通过自己的努…...

【Python数据分析】数据分析之numpy基础
实验环境:建立在Python3的基础之上 numpy提供了一种数据类型,提供了数据分析的运算基础,安装方式 pip install numpy导入numpy到python项目 import numpy as np本文以案例的方式展示numpy的基本语法,没有介绍语法的细枝末节&am…...

Swift 如何从图片数据(Data)检测原图片类型?
功能需求 如果我们之前把图片对应的数据(Data)保持在内存或数据库中,那么怎么从 Data 对象检测出原来图片的类型呢? 如上图所示:我们将 11 张不同类型的图片转换为 Data 数据,然后从 Data 对象正确检测出了原图片类型。 目前,我们的代码可以检测出 jpeg(jpg), tiff,…...

【ES6】 JavaScript 中的Object.assign
Object.assign() 是 JavaScript 中的一个方法,它用于复制源对象的所有可枚举属性到目标对象。该方法会返回目标对象。 这是其基本用法: let target Object.assign({}, source);在这个例子中,source 对象的所有可枚举属性都被复制到了 targ…...

Redis缓存和持久化
目录 Redis缓存 什么是缓存 缓存更新策略编辑 业务场景 缓存穿透 常见的解决方案 缓存雪崩 解决方案 缓存击穿 解决方案 Redis持久化 RDB持久化 执行时机 RDB方式bgsave的基本流程 AOF持久化 RDB和AOF的对比编辑 Redis主从 数据同步原理 总结 Redis缓存 …...
:多通道分离与合并)
OpenCV(六):多通道分离与合并
目录 1.多通道分离split() 2.多通道合并merge() 3.Android JNI demo 1.多通道分离split() void cv::split ( InputArray m, OutputArrayOfArrays mv ) m:待分离的多通道图像。 mv:分离后的单通道图像,为向量vector形式。 2.多通道合并merge…...

Sql单行数据查询为多行
数据量小可以,数据量大时间太久 select distinct regexp_substr("fixed_option", [^,],1,level) c1 from "MATERIAL"."BasicInfo_Dishes_Summary" A where "fixed_option" is not NULL AND "dish_name"地三鲜…...
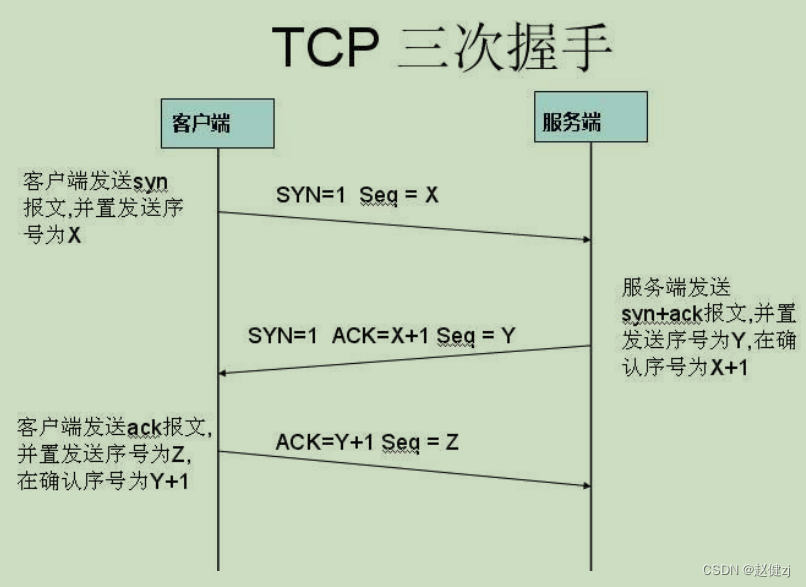
网络协议分析-http/https/tcp/udp
文章目录 TCP三次握手/TCP三次挥手TCP三次握手TCP四次挥手完整报文 实例代码HttpSampleClientHttpSampleServerHttpsSampleClientHttpsSampleServerTcpSampleClientTcpSampleServerUdpSampleClientUdpSampleSever 资料 TCP三次握手/TCP三次挥手 “三次握手”的目的是“为了防止…...

基于aarch64分析kernel源码 四:printk 内核打印
一、参考 Message logging with printk — The Linux Kernel documentation 如何获得正确的printk格式占位符 — The Linux Kernel documentation 使用printk记录消息 — The Linux Kernel documentation printk 内核打印 – 人人都懂物联网 (getiot.tech) 内核printk原理…...

机器人中的数值优化(六)—— 线搜索最速下降法
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...

postman调试注意事项
Postman是一个强大的API调试工具,它可以帮助开发人员测试和调试API端点,以确保它们按预期工作。在使用Postman进行接口调试时,以下是一些注意事项和可能出现的问题,以及如何解决这些问题。 确保请求参数正确 在测试API接口时&am…...

【C#】泛型
【C#】泛型 泛型是什么 泛型是将类型作为参数传递给类、结构、接口和方法,这些参数相当于类型占位符。当我们定义类或方法时使用占位符代替变量类型,真正使用时再具体指定数据类型,以此来达到代码重用目的。 泛型特点 提高代码重用性一定…...

CLIP:连接文本-图像
Contrastive Language-Image Pre-Training CLIP的主要目标是通过对比学习,学习匹配图像和文本。CLIP最主要的作用:可以将文本和图像表征映射到同一个表示空间 这是通过训练模型来预测哪个图像属于给定的文本,反之亦然。在训练过程中&#…...
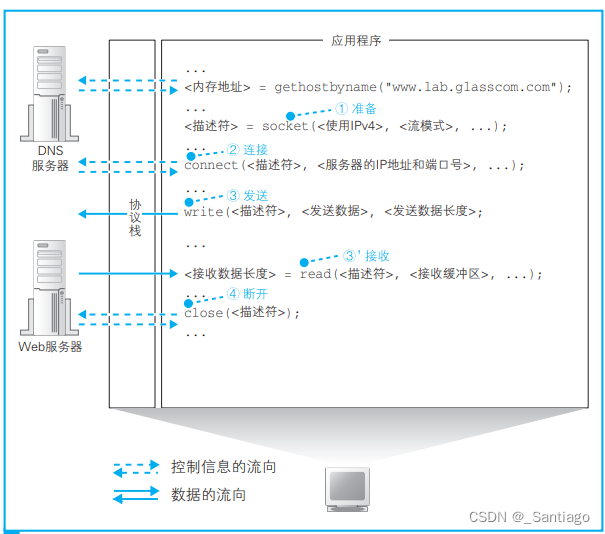
MFC网络编程简单例程
目录 一、关于网络的部分概念1 URL(网址)及URL的解析2 URL的解析3 域名及域名解析3 IP及子网掩码4 什么是Web服务器5 HTTP的基本概念6 Socket库概念7 协议栈8 Socket库收发数据基本步骤 二、基于TCP的网络应用程序三、基于UDP的网络应用程序 一、关于网络的部分概念 1 URL(网址…...
)
云原生简介 (Cloud Native)
云原生(cloud Native) 云原生的概念诞生于10年前,netflix 在 AWS 上的一次演讲中。有趣的是当初没有明确的定义,现在也没有明确的定义,对不同的人来说,有不同的概念。 概念 云原生:是在云上构…...
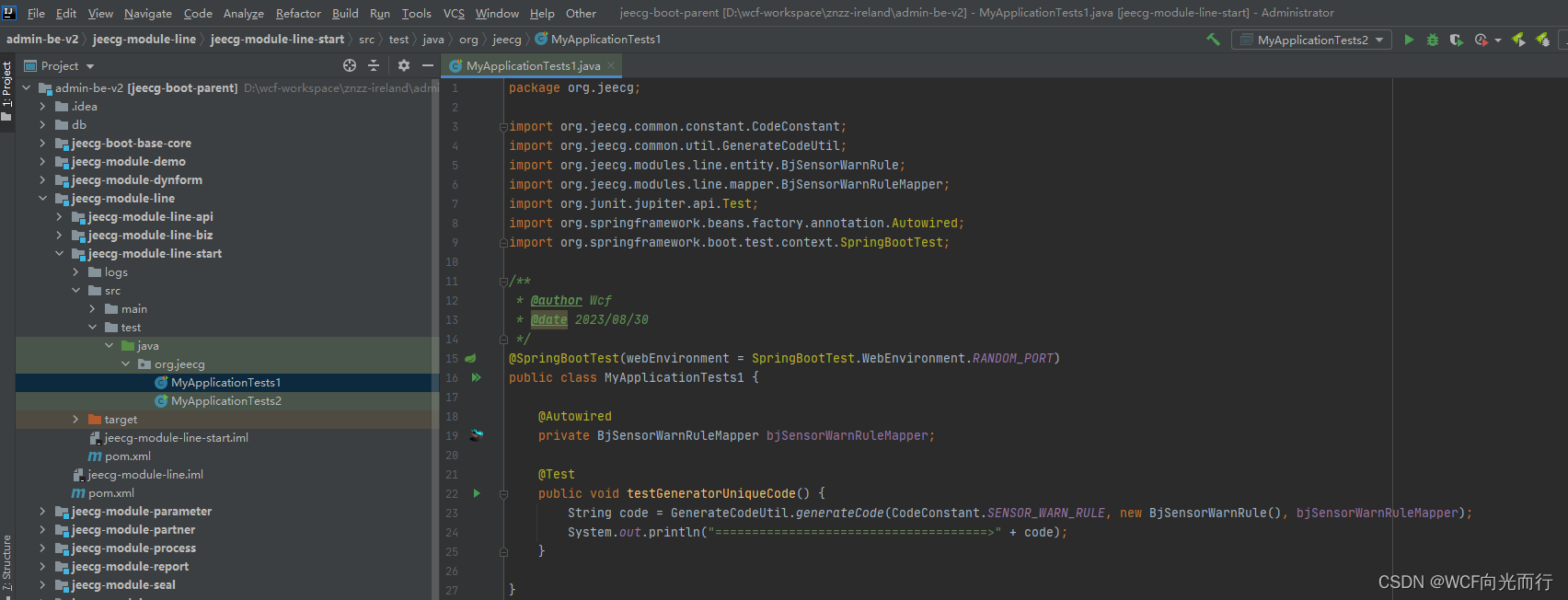
【SpringBoot系列】 测试框架之@SpringBootTest的使用
SpringBootTest的详细介绍 SpringBootTest 是 Spring Boot 测试框架中的注解,用于标识一个测试类,以指示该类是一个 Spring Boot 应用程序的测试类。它允许你在测试环境中加载整个 Spring Boot 应用程序上下文,测试应用程序的各种组件、服务…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
