机器人中的数值优化(六)—— 线搜索最速下降法
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
八、线搜索最速下降法
1、最速梯度下降法简介
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。在机器学习中,基于基本的梯度下降法发展了两种梯度下降方法,分别为随机梯度下降法和批量梯度下降法。
最速梯度下降法利用函数的一阶信息局部的去找一个让函数下降最快的方向,然后沿着这个方向不断的逼近局部极小值
对于有梯度的函数而言,最速下降的方向一定是其梯度的反方向(如下图中的蓝色箭头所示)

如果梯度存在,沿着梯度的反方向去更新一个x,一定会更接近于局部极小值,迭代格式如下式所示,其中τ是步长, ∇ f ( x k ) \nabla\text{}f\left(x^k\right)\quad\text{} ∇f(xk)是梯度或最小范数次梯度(次梯度集合里面模长最小的那个向量取反方向)
x k + 1 = x k − τ ∇ f ( x k ) x^{k+1}=x^{k}-τ\nabla\text{}f\left(x^k\right)\quad\text{} xk+1=xk−τ∇f(xk)

2、最速梯度下降法流程

3、步长τ的选取
① 策略1:τ取固定常量,如1、0.1、0.01等
② 策略2:τ取递减量,随着搜索的次数增加而减小
③ 策略3:精确线搜索,理想的方式,每次搜索的步长都沿着搜索方向让多元函数的截面到达最低点,称为最佳步长,沿着搜索方向下降最多的步长。然而找最佳步长本身就是一个优化的问题。
④ 策略4:非精确线搜索,将策略3的条件进行弱化,使得搜索步长不需要解决子优化问题,也可以快速的搜索

内容补充:一阶方向导数表示函数在该点处沿着方向d的函数值的变化率,可表示成如下的形式
∂ f ( x ) ∂ d = 1 ∥ d ∥ ∇ f ( x ) T d ; \frac{\partial f\left(x\right)}{\partial d}=\frac{1}{\left\|d\right\|}\nabla f(x)^{T}d; ∂d∂f(x)=∥d∥1∇f(x)Td;
(1)策略①, τ取固定常量时,若步长太大,可能振荡发散;步长太小,可能收敛过慢,当步长恰当时,快速收敛。因此固定步长策略需要依靠经验设定合适的步长,如下图所示:

(2) 策略②的稳定性较强,但收敛速度较慢,一般用于对函数的条件很差的时候,并且对于求解速率和时间没什么要求的时候。
(3) 策略④,我们可以沿着搜索方向d,把周围的函数 f ( x k ) f(x^{k}) f(xk)解出一个一维的函数,这个函数的意思就是,当步长取α时,对应函数的高度就是图中曲线,φ(0)值是 f f f在 f ( x k ) f(x^{k}) f(xk)处的初始值

如果仅是让函数下降的话,跟初始值φ(0)齐平以下的所有区域都可以选,如下图所示的0~α2区域,但是为了更快的下降,需要更严苛的条件,这个条件是跟梯度有关的,比如若局部极小值为1,而当前解为1.001,无论如何不能让函数的下降大于0.001,因此,我们要根据函数当前的梯度或者斜域来定充分下降的斜对数,它的斜率就是φ(0)的斜率,即搜索方向d与 x k x^{k} xk处梯度的点积 d T ∇ f ( x k ) d^{\mathrm{T}}\nabla f(x^{k}) dT∇f(xk),再乘以一个0~1的系数c对其进行放松,得到一个更小的区间0 ~ α1,一般来说,我们需要找一个不接近于0的步长,在这个Armijo condition 区域内搜索一个较靠右的步长,即我们想要的步长。

对于非凸函数的可接受区域如下图所示:

4、最速下降法流程及策略③和④的比较
给定一个x0,首先求他的梯度,取负梯度为它的搜索方向,然后利用二分法不断的二分α区间去找一个满足Armijo condition的步长α,然后接受他,去更新下一个x的位置,不断的循环,当f在xk处的梯度的模长足够小时,结束循环。(当不可微时,梯度改为次微分检验,即含零向量时,即可结束循环)

策略③只有找到上图中的最低点时,才进行更新,而策略④只要找到的步长位于Armijo condition 区域内即可进行更新。这样会节省一些时间,而且更简单一些,在工程中策略④更常用
从下图中可以看出,若采用精确线搜索(策略③),只需要寥寥几步更新就可以收敛较理想的状态,若采用充分下降线搜索(策略④)可能需要迭代多次更新,但是精确线搜索每次迭代花费算力较多,时间较长,而充分下降搜索耗时较少,所以总的花费时间≈单次耗时x迭代次数。两种策略的总耗时是近似的。

在下图所示的这样一个100维的凸函数的例子中,当精度要求比较高时,如0.0001,两种策略的迭代次数近似,而策略③的每次迭代耗时多于策略④

5、最速下降法的收敛速度
u在G度量意义下的范数 ∥ u ∥ G 2 \|u\|_G^2 ∥u∥G2定义为:(其中G为Hesse矩阵)
∥ u ∥ G 2 = u T G u . \|u\|_G^2={u}^\mathrm{T}Gu. ∥u∥G2=uTGu.
对正定二次函数,最速下降方法的收敛速度为
∥ x k + 1 − x ∗ ∥ G 2 ∥ x k − x ∗ ∥ G ⩽ ( λ max − λ min λ max + λ min ) 2 . \frac{\|x_{k+1}-x^*\|_G^2}{\|x_k-x^*\|_G}\leqslant\left(\frac{\lambda_{\text{max}}-\lambda_{\text{min}}}{\lambda_{\text{max}}+\lambda_{\text{min}}}\right)^2. ∥xk−x∗∥G∥xk+1−x∗∥G2⩽(λmax+λminλmax−λmin)2.
上式中有 :(其中 cond ( G ) = ∥ G ∥ ∥ G − 1 ∥ \operatorname{cond}(G)=\|G\|\|G^{-1}\| cond(G)=∥G∥∥G−1∥称为矩阵G的条件数)
λ max − λ min λ max + λ min = c o n d ( G ) − 1 c o n d ( G ) + 1 ≜ μ \frac{\lambda_{\max}-\lambda_{\min}}{\lambda_{\max}+\lambda_{\min}}=\frac{\mathrm{cond}(G)-1}{\mathrm{cond}(G)+1}\triangleq\mu λmax+λminλmax−λmin=cond(G)+1cond(G)−1≜μ.
由上式可以看出,最速下降方法的收敛速度依赖于G的条件数.当G的条件数接近于1时, u接近于零,最速下降方法的收敛速度接近于超线性收敛速度;而G的条件数越大,u越接近于1,该方法的收敛速度越慢.
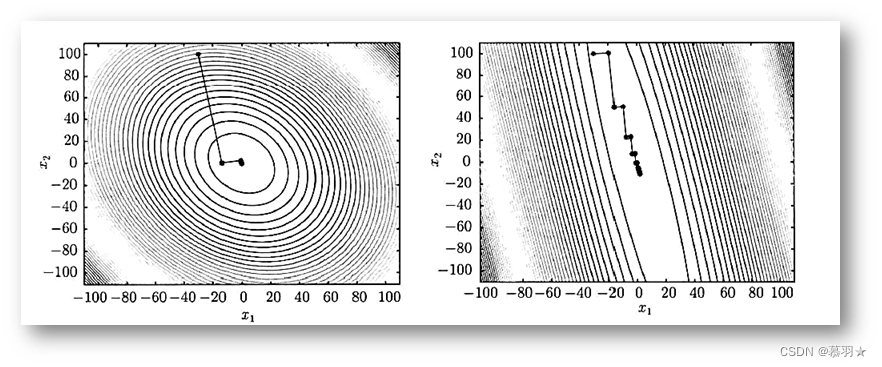
Hesse矩阵G的条件数的差异造成了最速下降方法对如下图所示的两个问题收敛速度的差异.在下图可以看出,最速下降方法相邻两步的迭代方向互相垂直,Hesse矩阵的条件数越大,二次函数一族椭圆的等高线越扁.可以想象,当目标函数的等高线为一族很扁的椭圆时,迭代在两个相互垂直的方向上交替进行.如果这两个方向没有一个指向极小点,迭代会相当缓慢,甚至收敛不到极小点.
6、最速下降法的优缺点
(1)缺点
当一个凸函数的条件数等于2时,等高线是一系列的椭圆,他的梯度是垂直于椭圆的边界的,如果条件数很大,椭圆就很扁,用最速下降法来迭代就会产生一些震荡。

当条件数更大,如100时,椭圆会更扁,由于梯度方向与等高线垂直,导致梯度方向近似于平行,需要震荡很久才能收敛到局部极小值。所以当函数的曲率很大,或者条件数很大的时候,采用梯度下降法可能需要很多的迭代次数。

下图是一个二维的二次函数的例子,从图中可以看出,随着条件数的增大,收敛所需的迭代次数也随之增加

(2)优点
最速下降方法的优点是:算法每次迭代的计算量少,存储量亦少; 即使从一个不太好的初始点出发,算法产生的迭代点也可能接近极小点.
参考资料:
1、机器人中的数值优化
2、梯度下降
3、数值最优化方法(高立 编著)
相关文章:

机器人中的数值优化(六)—— 线搜索最速下降法
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...

postman调试注意事项
Postman是一个强大的API调试工具,它可以帮助开发人员测试和调试API端点,以确保它们按预期工作。在使用Postman进行接口调试时,以下是一些注意事项和可能出现的问题,以及如何解决这些问题。 确保请求参数正确 在测试API接口时&am…...

【C#】泛型
【C#】泛型 泛型是什么 泛型是将类型作为参数传递给类、结构、接口和方法,这些参数相当于类型占位符。当我们定义类或方法时使用占位符代替变量类型,真正使用时再具体指定数据类型,以此来达到代码重用目的。 泛型特点 提高代码重用性一定…...

CLIP:连接文本-图像
Contrastive Language-Image Pre-Training CLIP的主要目标是通过对比学习,学习匹配图像和文本。CLIP最主要的作用:可以将文本和图像表征映射到同一个表示空间 这是通过训练模型来预测哪个图像属于给定的文本,反之亦然。在训练过程中&#…...
MFC网络编程简单例程
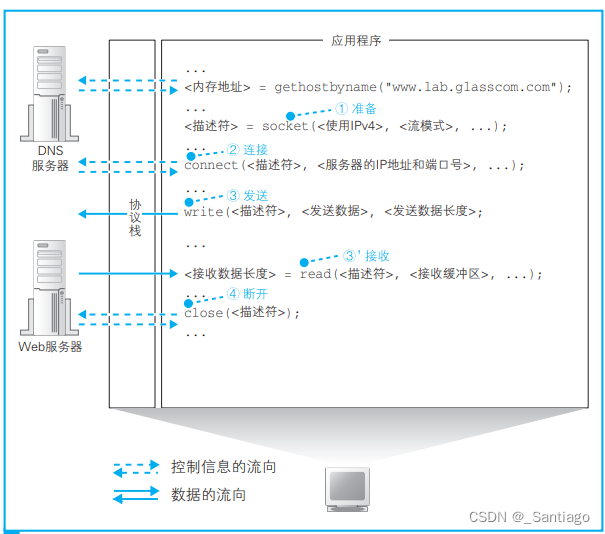
目录 一、关于网络的部分概念1 URL(网址)及URL的解析2 URL的解析3 域名及域名解析3 IP及子网掩码4 什么是Web服务器5 HTTP的基本概念6 Socket库概念7 协议栈8 Socket库收发数据基本步骤 二、基于TCP的网络应用程序三、基于UDP的网络应用程序 一、关于网络的部分概念 1 URL(网址…...
)
云原生简介 (Cloud Native)
云原生(cloud Native) 云原生的概念诞生于10年前,netflix 在 AWS 上的一次演讲中。有趣的是当初没有明确的定义,现在也没有明确的定义,对不同的人来说,有不同的概念。 概念 云原生:是在云上构…...
【SpringBoot系列】 测试框架之@SpringBootTest的使用
SpringBootTest的详细介绍 SpringBootTest 是 Spring Boot 测试框架中的注解,用于标识一个测试类,以指示该类是一个 Spring Boot 应用程序的测试类。它允许你在测试环境中加载整个 Spring Boot 应用程序上下文,测试应用程序的各种组件、服务…...
【数据结构与算法篇】手撕八大排序算法之交换排序
👻内容专栏: 《数据结构与算法篇》 🐨本文概括:常见交换排序包括冒泡排序与快速排序,本篇讲述冒泡排序与快速排序的思想及实现、复杂度分析。 🐼本文作者: 花 蝶 🐸发布时间&#…...
ArcGIS Pro实践技术应用、制图、空间分析、影像分析、三维建模、空间统计分析与建模、python融合
GIS是利用电子计算机及其外部设备,采集、存储、分析和描述整个或部分地球表面与空间信息系统。简单地讲,它是在一定的地域内,将地理空间信息和 一些与该地域地理信息相关的属性信息结合起来,达到对地理和属性信息的综合管理。GIS的…...

uniapp 项目实践总结(一)uniapp 框架知识总结
导语:最近开发了一个基于 uniapp 框架的项目,有一些感触和体会,所以想记录以下一些技术和经验,在这里做一个系列总结,算是对自己做一个交代吧。 目录 简介全局文件全局组件常用 API条件编译插件开发 简介 uniapp 是…...

Oracle查看与修改隐藏参数
Oracle查看与修改隐藏参数 查看隐藏参数修改隐藏参数 查看隐藏参数 查看数据库中所有的隐藏参数: SELECT a.ksppinm "Parameter", b.KSPPSTDF "Default Value",b.ksppstvl "Session Value", c.ksppstvl "Instance Value"…...

基于MQTT协议的物联网网关实现远程数据采集及监控
在数字化时代的浪潮中,工业界正面临着前所未有的变革与机遇。而在这场变革中,基于MQTT协议的物联网网关崭露头角,成为连接工业设备、实现远程数据采集与监控的利器。其中,HiWoo Box作为一款出色的工业边缘网关,引领着这…...

服务内部错误: stderr: bash: docker-compose: 未找到命令
报错描述 1Panel在应用商店安装软件失败,重建或者重启报错"服务内部错误: stderr: bash: docker-compose: 未找到命令" 执行命令"docker-compose --version"结果为"Docker Compose version v2.17.2",说明docker-compose已…...

自然语言处理(六):词的相似性和类比任务
词的相似性和类比任务 在前面的章节中,我们在一个小的数据集上训练了一个word2vec模型,并使用它为一个输入词寻找语义相似的词。实际上,在大型语料库上预先训练的词向量可以应用于下游的自然语言处理任务,为了直观地演示大型语料…...

安防监控视频平台EasyCVR视频汇聚平台定制项目增加AI智能算法详细介绍
安防视频集中存储EasyCVR视频汇聚平台,可支持海量视频的轻量化接入与汇聚管理。平台能提供视频存储磁盘阵列、视频监控直播、视频轮播、视频录像、云存储、回放与检索、智能告警、服务器集群、语音对讲、云台控制、电子地图、平台级联、H.265自动转码等功能。为了便…...

VB个人邮件处理系统设计与实现
简述 当今世界电子邮件已经是网络生活中不可或缺的,相信每个认知网络的人都会有一个或多个自己的电子邮箱,人们通过电子邮件进行通信和交流,许多商家和组织机构也用电子邮件进行各种商业活动和业务联系,毫无疑问,电子邮件已经逐渐开始取代普通的信件,成为为主流的信件交流…...
第一章辩证唯物论,考点七思维导图
逻辑框架 考点七思维导图:...
)
Python入门教程 - 基本函数(四)
目录 一、什么是函数 二、自定义函数并使用它 一、什么是函数 前面我们学习了像input()、print()、type()等等,他们都是函数。这些其实是由Python内部帮我们定义好的。我们直接用就可以了。 关于函数,除了用内部定义好的,我们也可以自己定…...
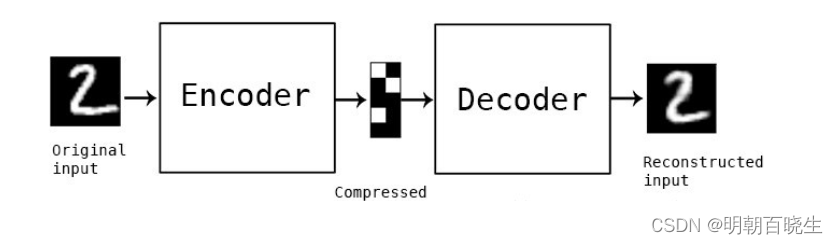
[PyTorch][chapter 53][Auto Encoder 实战]
前言: 结合手写数字识别的例子,实现以下AutoEncoder ae.py: 实现autoEncoder 网络 main.py: 加载手写数字数据集,以及训练,验证,测试网络。 左图:原图像 右图:重构图像 ----main----- 每轮训…...

Springboot常用方法参数注解及示例
文章目录 Springboot常用方法参数注解及示例一、RequestParam: 从URL查询参数中提取数据。二、PathVariable: 从URL路径中提取数据。三、RequestBody: 从请求体中提取数据,并映射到对象。四、RequestHeader: 从请求头中…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...
