5.1 树和二叉树的定义
思维导图:



问题 为什么有树和二叉树?
"树" 和 "二叉树" 都是数据结构中常用的结构,它们分别有其独特的应用和优点。我们可以从它们的定义和特性中理解为什么它们都存在。
1. **树 (Tree):**
- **定义**: 树是一个由n个节点组成的集合,每个节点最多只有一个父节点,并且有一个特殊的节点,称为根。
- **应用**:
- 文件系统,其中每个文件或文件夹可以包含多个文件或文件夹。
- 组织结构图,其中一个经理可能有多个直接下属。
- 抽象语法树,通常在编译器中使用,表示源代码的结构。
- **优点**:
- 可以表示不同数量的子节点的数据结构。
- 可以模拟现实生活中的多种结构。
2. **二叉树 (Binary Tree):**
- **定义**: 二叉树是一个特殊的树,其中每个节点最多只有两个子节点:左子节点和右子节点。
- **应用**:
- 二叉搜索树,用于搜索、插入、删除操作的快速执行。
- 堆结构,如最大堆和最小堆,用于优先队列。
- 平衡二叉树,如AVL或红黑树,确保树保持平衡,以获得更好的性能。
- **优点**:
- 由于其结构简单和有序,使得许多算法(如搜索、插入、删除等)在二叉树上更高效。
- 二叉树有助于保持数据平衡,而不是高度偏斜,从而提高算法的效率。
总结:
- **为什么有树**? 树结构非常适合于表示现实世界中的许多层次或分级关系,其中一个元素可以有多个子元素。
- **为什么有二叉树**? 二叉树是一个特殊且简化的树形结构,特别适合于计算机科学中的某些应用,因为它简化了许多算法,并能够高效地实现它们。
两者之间的选择取决于所需的应用和操作的特性。
前言:
这段话主要讲述了树结构和二叉树在计算机科学中的重要性和应用。以下是该段内容的简要概述:
1. **定义和重要性**:
- 树结构是非线性的数据结构。
- 树通过分支关系定义了一个层次结构。
- 树结构不仅在计算机科学中重要,在实际生活中(如社会的族谱和组织结构)也有其影子。
2. **在计算机领域的应用**:
- 树,特别是二叉树,广泛应用于计算机领域。
- 操作系统中用树来表示文件的目录结构。
- 编译系统中,树用来表示源代码的语法结构。
- 在数据库系统中,树是组织信息的主要方式之一。
3. **本章的内容重点**:
- 主要讨论二叉树的存储结构及其操作。
- 研究了树和森林与二叉树之间的转换关系。
- 最后,介绍了树的实际应用。
总的来说,这段话强调了树结构,尤其是二叉树在计算机科学中的中心地位,并预告了本章将详细讨论的相关主题。
5.1.1 树的定义
**5.1 树和二叉树的定义**
- **5.1.1 树的定义**
树是一个由节点组成的有限集合,它可以是空的(无节点)或包含一个称为“根”的特殊节点,与其他可以分割为多个互不相交子集的节点,其中每个子集本身也是一个树。这种定义是递归的,即树的定义是基于树本身的子集定义的。
- 图5.1(a) 是一个只有一个节点的树,即只有一个根节点。
- 图5.1(b) 是一个复杂点的树,它有13个节点,其中A是根。除根节点A外的节点可以分为3个子集: Ti, T₂, T3,这些都是根A的子树。
有多种方式可以表示树,例如:
- 图5.2(a) 是通过嵌套集合表示的树。
- 图5.2(b) 是使用广义表来表示的树。
- 图5.2(c) 是用凹入表示法表示的。
这些示例和描述突显了树结构在日常生活和计算机程序设计中的重要性。在实际中,任何分等级的分类方案都可以用树结构来表示。
**基本术语**:
- **节点(Node)**: 树中的每一个元素称为节点。
- **根节点(Root Node)**: 没有父节点的节点。
- **叶节点(Leaf Node)**: 没有子节点的节点。
- **子树(Subtree)**: 任一节点与其下级全部节点构成的树称为该节点的子树。
- **父节点(Parent Node)**: 除根节点外,每个节点有且只有一个与它直接上级关联的节点。
- **孩子节点(Child Node)**: 与节点直接下级关联的节点称为它的孩子节点。
- **兄弟节点(Sibling Nodes)**: 具有相同父节点的两个或多个节点。
- **节点的层次(Level)**: 根节点的层次定义为1,其余节点的层次是其父节点的层次加1。
这些术语帮助我们更好地理解和描述树的结构和性质。
5.1.2 树的基本术语
你提供了关于“树”的一些基本术语和定义,下面是这些内容的简明总结:
**5.1.2 树的基本术语**
1. **节点(Node)**:树中的独立单元,包含数据元素和指向其子树的分支。
2. **节点的度(Degree of Node)**:一个节点有多少个子树。
3. **树的度(Degree of Tree)**:树中最大的节点度。
4. **叶子(Leaf or Terminal Node)**:没有子节点的节点。
5. **非终端节点(Non-terminal or Internal Node)**:有一个或多个子节点的节点。
6. **双亲和孩子(Parent and Child)**:一个节点的子节点称为其孩子,反之则为双亲。
7. **兄弟(Siblings)**:具有相同父节点的节点。
8. **祖先(Ancestor)**:从根到某一节点路径上的所有节点。
9. **子孙(Descendant)**:某一节点的所有下级节点。
10. **层次(Level)**:从根开始,每一个节点的层次是其父节点的层次加1。
11. **堂兄弟(Cousins)**:其双亲在同一层的节点。
12. **树的深度(Depth or Height of Tree)**:树中节点的最大层次。
13. **有序树和无序树(Ordered and Unordered Trees)**:树中节点的子树有固定次序的是有序树,没有固定次序的是无序树。
14. **森林(Forest)**:多棵互不相交的树的集合。
这些术语为我们提供了一个框架来描述和理解树的结构和属性。特别是在计算机科学和数据结构中,这些定义和概念对于算法的设计和理解非常重要。

5.1.3 二叉树的定义
**5.1.3 二叉树的定义**
**二叉树 (Binary Tree)**:由n个节点组成的集合,可以为空(n=0)或由以下两部分组成:
1. **根节点**:二叉树中唯一的起始节点。
2. **左、右子树**:除根节点外的所有节点可以被分为两个互不相交的子集,分别为左子树和右子树,且它们自身也是二叉树。
**二叉树与常规树的主要区别**:
1. 在二叉树中,每个节点最多只有两个子节点。
2. 二叉树的左、右子树有明确的区分,并且次序不能被颠倒。
**二叉树的五种基本形态**(如图5.3所示):
a. 空的二叉树。
b. 只有一个根节点的二叉树。
c. 只有左子树的二叉树(右子树为空)。
d. 左、右子树都不为空的二叉树。
e. 只有右子树的二叉树(左子树为空)。
注意:在二叉树中,所有关于“树”的术语(如在5.1.2节中描述的)都适用。
二叉树是数据结构中最常见和最基础的结构之一,它被广泛应用于算法设计,如排序算法、搜索算法等。它的递归性质为理解和应用带来了方便。
 例子:
例子:
好的,让我们来看三个二叉树的应用示例:
### 1. 二叉搜索树(BST)
**分析思考**:
- 二叉搜索树是一个二叉树,其中每个节点都有一个键和一个关联的值。对于树中的每个节点:
* 所有左子树的键都小于节点的键。
* 所有右子树的键都大于节点的键。
- 这些属性确保了在BST中查找键的操作非常快。
#### C 实现:
typedef struct Node {int key;struct Node* left;struct Node* right;
} Node;Node* newNode(int item) {Node* temp = (Node*)malloc(sizeof(Node));temp->key = item;temp->left = temp->right = NULL;return temp;
}Node* insert(Node* root, int key) {if (root == NULL) return newNode(key);if (key < root->key)root->left = insert(root->left, key);else if (key > root->key)root->right = insert(root->right, key);return root;
}#### C++ 实现:
struct Node {int key;Node* left;Node* right;Node(int x) : key(x), left(nullptr), right(nullptr) {}
};Node* insert(Node* root, int key) {if (!root) return new Node(key);if (key < root->key)root->left = insert(root->left, key);else if (key > root->key)root->right = insert(root->right, key);return root;
}#### Java 实现:
、
public class Node {int key;Node left, right;public Node(int item) {key = item;left = right = null;}
}public Node insert(Node root, int key) {if (root == null) {root = new Node(key);return root;}if (key < root.key)root.left = insert(root.left, key);else if (key > root.key)root.right = insert(root.right, key);return root;
}### 2. 堆(特别是二叉堆)
**分析思考**:
- 二叉堆是一种特殊的完全二叉树,可以作为优先队列的有效数据结构。
- 最大堆:父节点的值总是大于或等于其子节点的值。
- 最小堆:父节点的值总是小于或等于其子节点的值。
- 这里为了简洁,我们只展示插入操作的C++版本实现。
#### C++ 实现:
#include <vector>class MaxHeap {
private:std::vector<int> heap;int parent(int i) { return (i - 1) / 2; }int left(int i) { return 2 * i + 1; }int right(int i) { return 2 * i + 2; }void siftUp(int i) {while (i > 0 && heap[parent(i)] < heap[i]) {std::swap(heap[parent(i)], heap[i]);i = parent(i);}}public:void insert(int key) {heap.push_back(key);int index = heap.size() - 1;siftUp(index);}
};### 3. 平衡二叉搜索树(例如AVL树)
**分析思考**:
- 在普通的二叉搜索树中,当你连续插入已排序的数据时,树可能会变得非常偏斜,导致查找、插入和删除的时间复杂度降为O(n)。
- 平衡二叉搜索树(例如AVL树)保持树的平衡状态,即确保树的左子树和右子树的高度差不会超过1。这保证了在平衡二叉搜索树中的操作始终保持O(log n)的时间复杂度。
#### C 实现:
typedef struct Node {int key;int height;struct Node* left;struct Node* right;
} Node;int height(Node* N) {if (N == NULL)return 0;return N->height;
}int max(int a, int b) {return (a > b) ? a : b;
}Node* newNode(int key) {Node* node = (Node*)malloc(sizeof(Node));node->key = key;node->left = node->right = NULL;node->height = 1;return node;
}Node* rightRotate(Node* y) {Node* x = y->left;Node* T2 = x->right;x->right = y;y->left = T2;y->height = max(height(y->left), height(y->right)) + 1;x->height = max(height(x->left), height(x->right)) + 1;return x;
}Node* leftRotate(Node* x) {Node* y = x->right;Node* T2 = y->left;y->left = x;x->right = T2;x->height = max(height(x->left), height(x->right)) + 1;y->height = max(height(y->left), height(y->right)) + 1;return y;
}int getBalance(Node* N) {if (N == NULL)return 0;return height(N->left) - height(N->right);
}Node* insert(Node* node, int key) {if (node == NULL)return newNode(key);if (key < node->key)node->left = insert(node->left, key);else if (key > node->key)node->right = insert(node->right, key);elsereturn node;node->height = 1 + max(height(node->left), height(node->right));int balance = getBalance(node);if (balance > 1 && key < node->left->key)return rightRotate(node);if (balance < -1 && key > node->right->key)return leftRotate(node);if (balance > 1 && key > node->left->key) {node->left = leftRotate(node->left);return rightRotate(node);}if (balance < -1 && key < node->right->key) {node->right = rightRotate(node->right);return leftRotate(node);}return node;
}#### C++ 实现:
class AVLNode {
public:int key;int height;AVLNode* left;AVLNode* right;AVLNode(int k) : key(k), height(1), left(nullptr), right(nullptr) {}
};class AVLTree {
private:AVLNode* root;int height(AVLNode* N) {if (!N) return 0;return N->height;}int balanceFactor(AVLNode* N) {if (!N) return 0;return height(N->left) - height(N->right);}AVLNode* rightRotate(AVLNode* y) { /*... Similar to C ...*/ }AVLNode* leftRotate(AVLNode* x) { /*... Similar to C ...*/ }public:AVLTree() : root(nullptr) {}void insert(int key) {root = insert(root, key);}AVLNode* insert(AVLNode* node, int key) { /*... Similar to C ...*/ }
};#### Java 实现:
class AVLNode {int key, height;AVLNode left, right;AVLNode(int d) {key = d;height = 1;}
}public class AVLTree {AVLNode root;int height(AVLNode N) {if (N == null)return 0;return N.height;}int getBalance(AVLNode N) {if (N == null)return 0;return height(N.left) - height(N.right);}AVLNode rightRotate(AVLNode y) { /*... Similar to C ...*/ }AVLNode leftRotate(AVLNode x) { /*... Similar to C ...*/ }AVLNode insert(AVLNode node, int key) { /*... Similar to C ...*/ }public void insert(int key) {root = insert(root, key);}
}上述代码只展示了部分实现,因为 AVL 树的完整实现包括其他操作,如删除节点,并且需要处理各种平衡情况。上述代码应该为你提供了一个基本的理解,但在实际应用中可能需要进一步的完善和优化。

相关文章:

5.1 树和二叉树的定义
思维导图: 问题 为什么有树和二叉树? "树" 和 "二叉树" 都是数据结构中常用的结构,它们分别有其独特的应用和优点。我们可以从它们的定义和特性中理解为什么它们都存在。 1. **树 (Tree):** - **定义**:…...
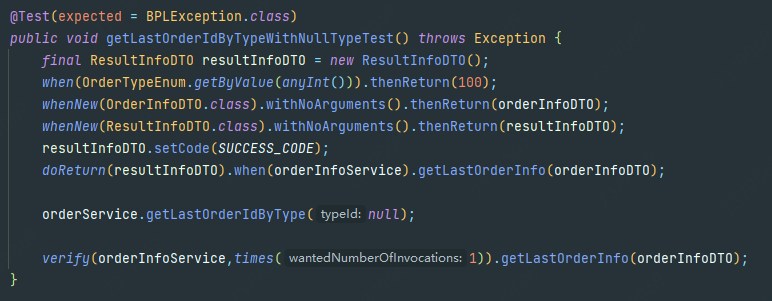
Java单元测试及常用语句 | 京东物流技术团队
1 前言 编写Java单元测试用例,即把一段复杂的代码拆解成一系列简单的单元测试用例,并且无需启动服务,在短时间内测试代码中的处理逻辑。写好Java单元测试用例,其实就是把“复杂问题简单化,建单问题深入化“。在编写的…...
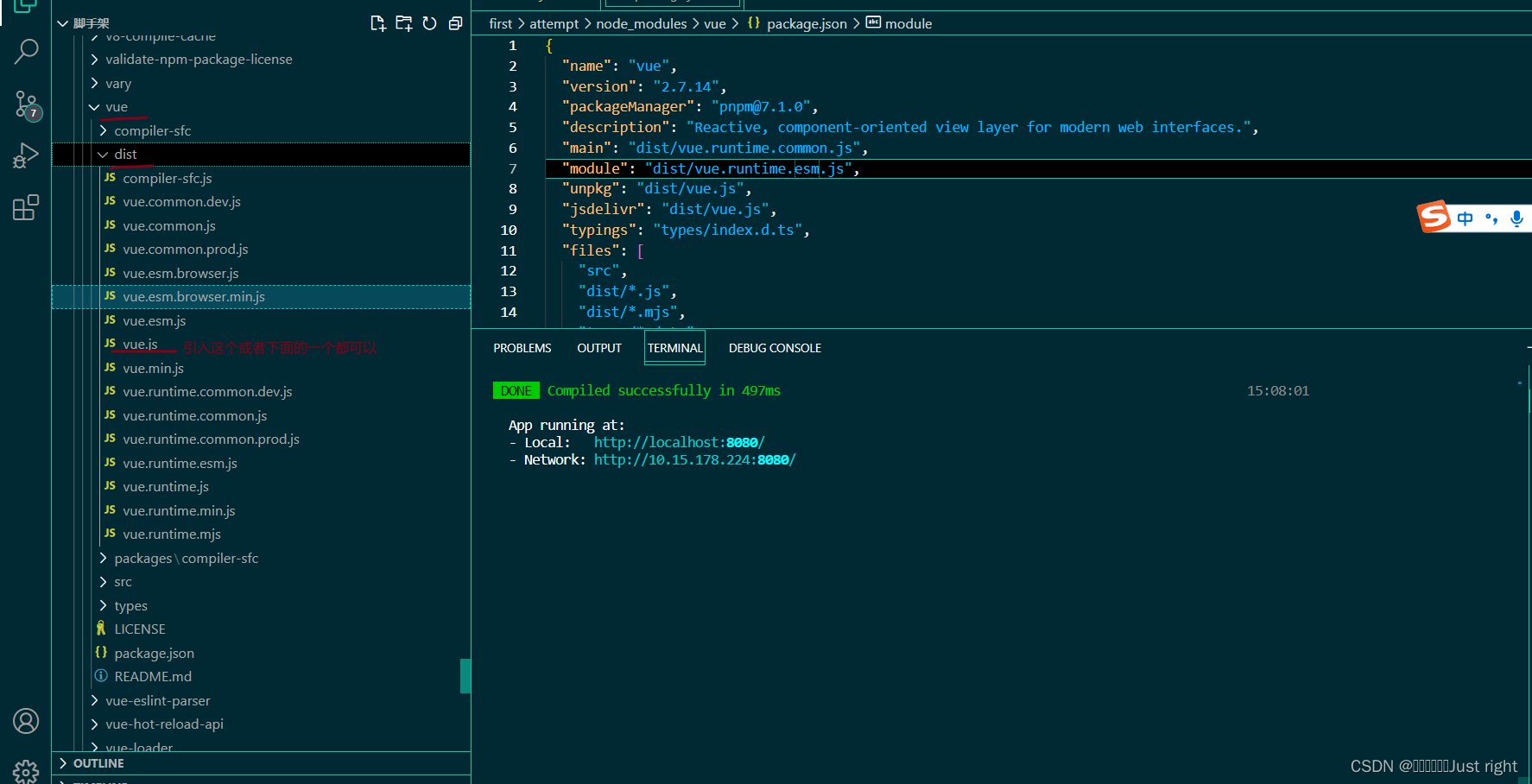
详解Vue中的render: h => h(App)
声明:只是记录,会有错误,谨慎阅读 我们用脚手架初始化工程的时候,main.js的代码如下 import Vue from vue import App from ./App.vueVue.config.productionTip falsenew Vue({// 把app组件放入容器中render: h > h(App), }).$mount(#ap…...

归并排序的详解!
本文旨在讲解归并排序的实现(递归及非递归)搬好小板凳,干货来了! 前序: 在介绍归并排序之前,需要给大家介绍的是什么是归并,归并操作,也叫归并算法,指的是将两个顺序序列…...

排盘程序算法探寻举例(陆先生八字)
算法实现: 1.庚生未月,燥土不能生金,日支申金为日主墙根,月干辛金比劫透出傍身,月干强。年干甲木自做寅木强根,又得月支乙木中气,甲木强旺有力,时干丙火七杀得未土余气,…...

考研408 | 【操作系统】终章
I/O设备的基本概念和分类 I/O设备: I/O设备的分类 1.按使用特性: 2.按传输速率分类: 3.按信息交换的单位分类: 总结: I/O控制器 I/O设备的机械部件: I/O设备的电子部件(I/O控制器&#…...
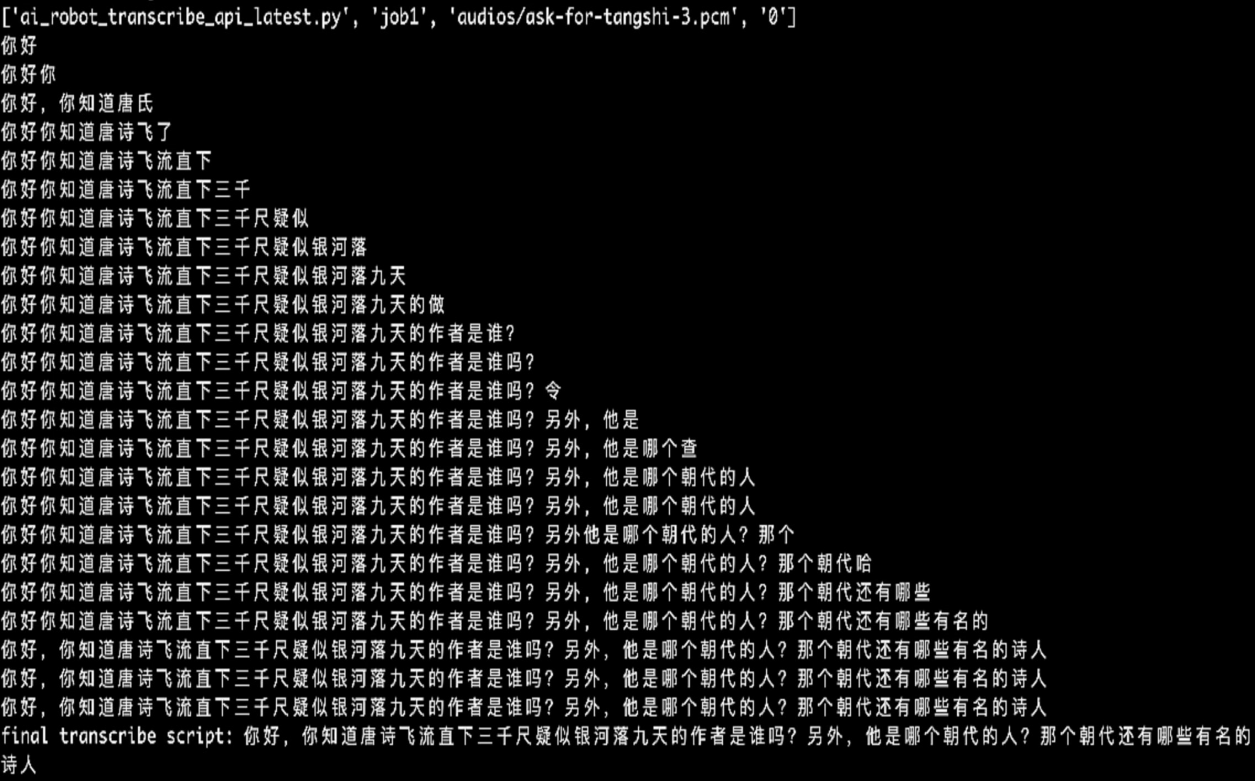
亚马逊云科技生成式AI技术辅助教学领域,近实时智能应答2D数字人搭建
早在大语言模型如GPT-3.5等的兴起和被日渐广泛的采用之前,教育行业已经在AI辅助教学领域有过各种各样的尝试。在教育行业,人工智能技术的采用帮助教育行业更好地实现教学目标,提高教学质量、学习效率、学习体验、学习成果。例如,人…...

Programming abstractions in C阅读笔记:p139-p143
《Programming Abstractions In C》学习第55天,p139-p140,总结如下: 一、技术总结 1.文件I/O操作 文件I/O操作可以分为一下这些步骤: (1)声明文件指针对象。 File *infile;(2)打开文件 fopen()。打开文件的模式有“r”, “w…...
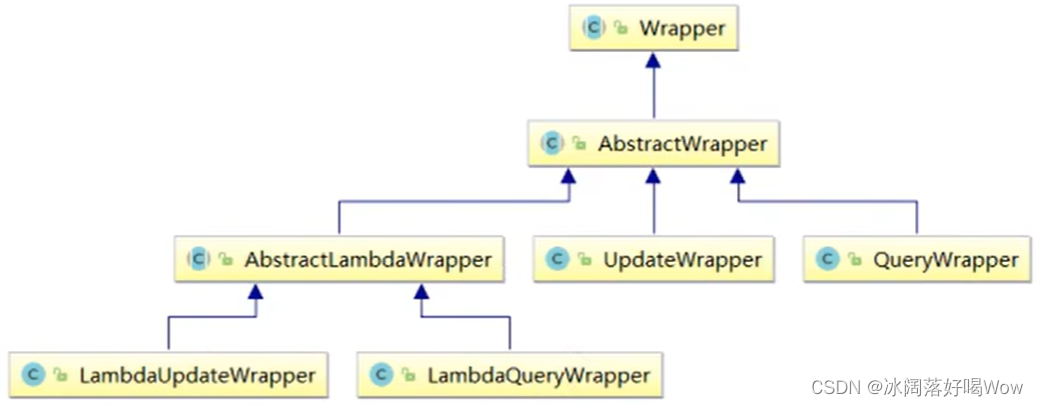
MyBatis-Plus学习笔记
1.MyBatis-Plus简介: MyBatis-Plus是一个MyBatis的增强工具,在MyBatis的基础上只做增强不做改变,为简化开发、提高效率而生。MyBatis-Plus提供了通用的mapper和service,可以在不编写任何SQL语句的情况下,快速的实现对单…...
linux安装docker全过程
3. 第二步:设置docker的存储库。就两条命令,我们直接执行就好。 sudo yum install -y yum-utils sudo yum-config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo 4. 安装docker engine和docker-compose。 执行命…...

Spring 中存取 Bean 的相关注解
目录 一、五大类注解 1、五大类注解存储Bean对象 1.1Controller(控制器储存) 1.2Service(服务存储) 1.3Repository(仓库存储) 1.4Component(组件存储) 1.5Configuration(配置存储) 2、五大类注解小结 2.1为什么要这么多类注解 2.2 五大类注解之间的关系 二、方法注解 1.方法注…...

Camunda 7.x 系列【38】表单服务 FormService
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot 版本 2.7.9 本系列Camunda 版本 7.19.0 源码地址:https://gitee.com/pearl-organization/camunda-study-demo 文章目录 1. 概述2. 演示2.1 获取流程开始表单2.2 启动流程2.3 查询任务表单2.4 完成任务3. 实际开发…...
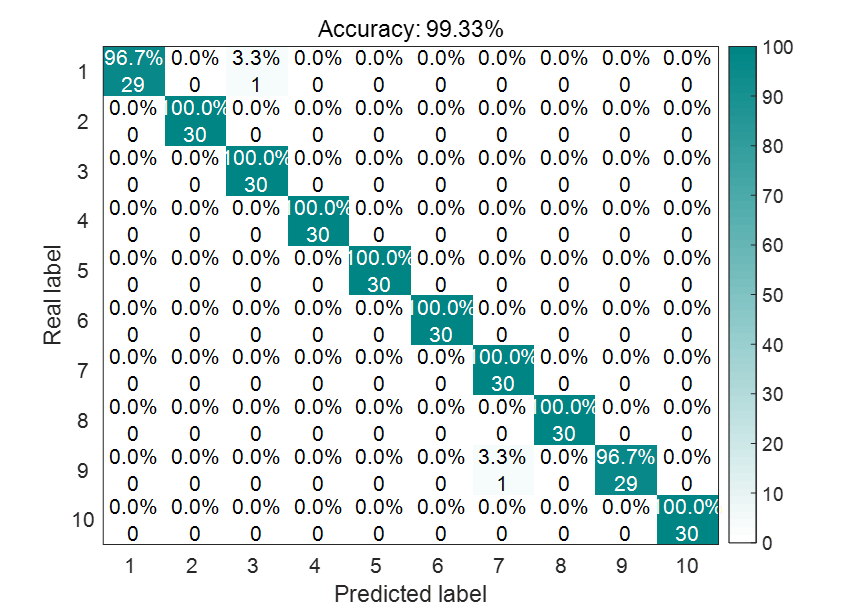
保姆级教程之SABO-VMD-SVM的西储大学轴承诊断
之前写过一篇优化核极限学习机的轴承诊断,今天再出一期基于SVM的轴承诊断。 依旧是包含了从数据处理,到减法优化器SABO算法优化VMD参数,再到支持向量机的故障诊断,实现故障诊断的全流程,其他类型的故障诊断均可参考此流…...
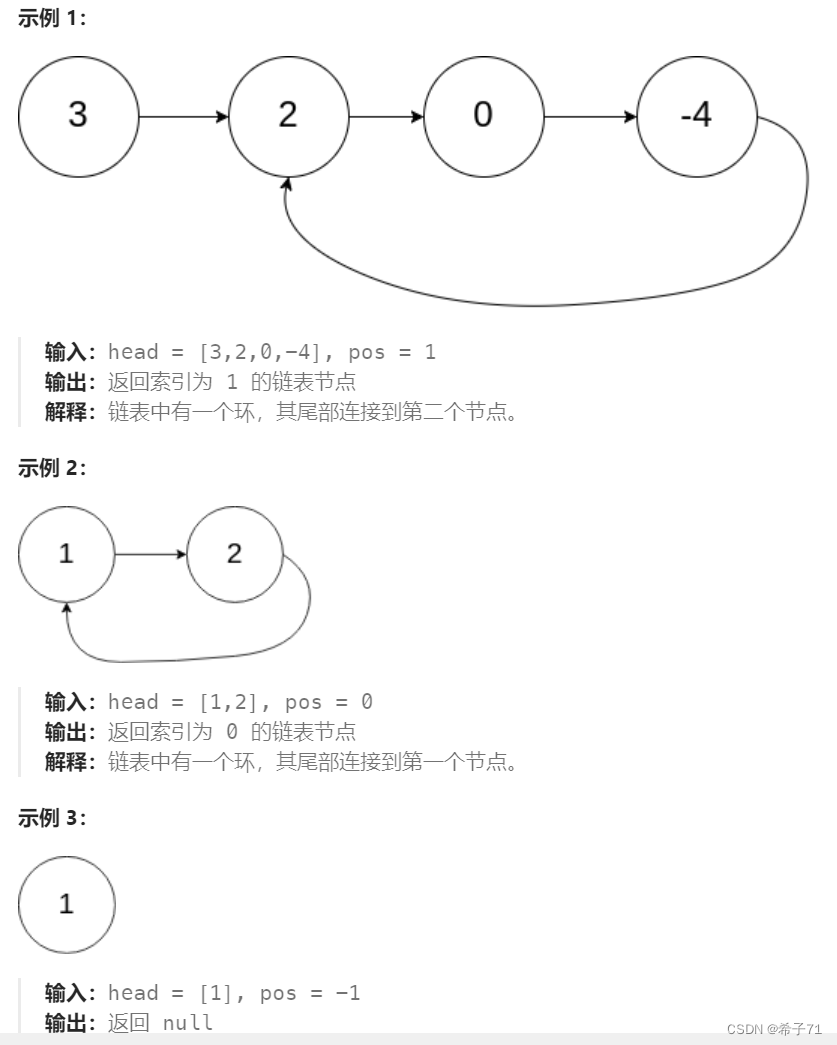
指向任意节点的带环链表
🌈图示指向任意节点的带环链表 如图: 🌈快慢指针法判断链表是否带环 🌟思路:快指针fast一次走2步,慢指针slow一次走1步,fast先进环在换中运动,随后slow进入环。两指针每同时移动…...
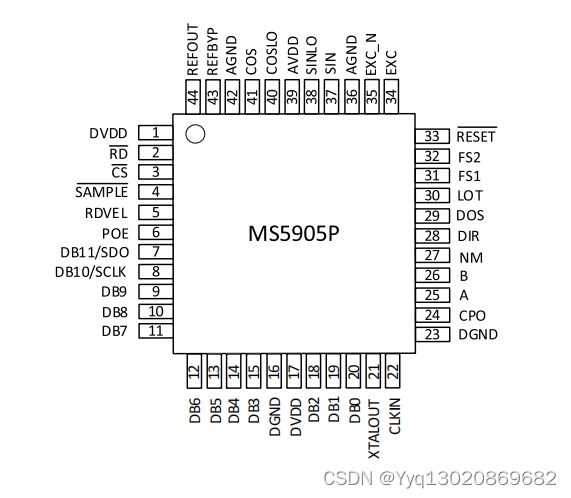
应用于伺服电机控制、 编码器仿真、 电动助力转向、发电机、 汽车运动检测与控制的旋变数字转换器MS5905P
MS5905P 是一款 12bit 分辨率的旋变数字转换器。 片上集成正弦波激励电路,正弦和余弦允许输入峰峰值 幅度为 2.3V 到 4.0V ,可编程激励频率为 10kHz 、 12kHz 、 15kHz 、 20kHz 。 转换器可并行或串行输出角度 和速度对应的数字量。 MS5905…...
)
Ansible学习笔记(持续更新)
Ansible学习目录 1.自动化运维1.1 企业实际应用场景1.1.1 Dev开发环境1.1.2 测试环境1.1.3 发布环境1.1.4 生产环境1.1.5 灰度环境 1.2 程序发布1.3 自动化运维应用场景1.4 常用自动化运维工具 2.Ansible介绍和架构2.1 Ansible特性2.2 Ansible架构2.2.1 Ansible主要组成部分2.2…...

CCF HPC China2023|澎峰科技:使能先进计算,赋能行业应用
CCF HPC China2023圆满落幕! 桂秋八月,为期三天的中国高性能计算领域最高规格盛会——2023CCF全球高性能计算学术年会(HPC China)在青岛红岛国际展览中心圆满落幕。行业超算大咖、顶级学界精英、先锋企业领袖参会者齐聚山东青岛&a…...

【FlowDroid】一、处理流程学习
FlowDroid 一、处理流程学习 下载配置源码概况代码逻辑分析analyzeAPKFilerunInfoflowprocessEntryPointcalculateCallbacks(sourcesAndSinks)再次回到processEntryPoint 自己做一些笔记 下载配置 参照我前面的文章可以使用FlowDroid安装初体验 为了看代码了解FlowDroid如何处…...
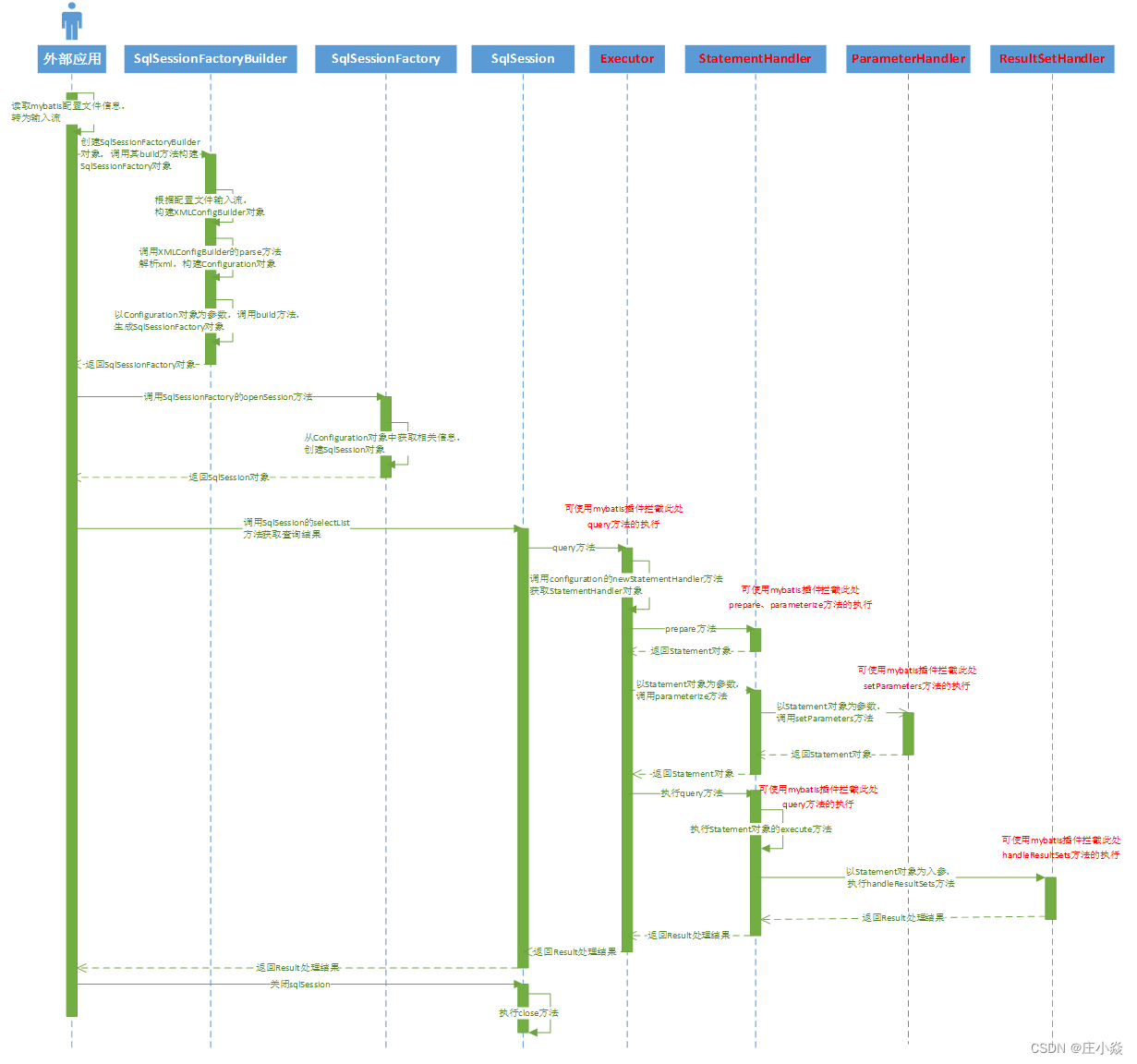
MyBatis——MyBatis插件原理
摘要 本博文主要介绍MyBatis插件机原理,帮助大家更好的理解和学习MyBatis。 一、插件机制概述 MyBatis 允许你在已映射语句执行过程中的某一点进行拦截调用。默认情况下,MyBatis允许使用插件来拦截的方法调用包括: Executor (update, que…...

简易虚拟培训系统-UI控件的应用5
目录 Toggle控件简介 示例-使用Toggle组实现主轴速度选择 本篇介绍UI控件Toggle,尝试一个小示例-使用单选框实现速度的选择控制。 Toggle控件简介 1. Toggle的结构如下:最重要的Toggle组件挂在Toggle节点上,下面的Image组件用于显示单选框…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...


