NTT功能与实现
NTT的基础功用与拓展功能:
1.evaluate和interpolate
evaluate的本质是选择n个点(假设f(x)的度为n),计算得到其值,因此根据定义可以直接进行代入计算。为了加快计算的过程选取 w n w_n wn的幂次(DFT问题即离散傅里叶变换),使用FFT算法来加快计算过程,将上述方法记作 N T T ( f ) NTT(f) NTT(f)
interpolate的本质是根据n个点值计算得到对应的系数,据此可以列出方程直接求解或者利用矩阵进行求解(根据插值多项式的唯一性,解唯一)。为了加快计算的过程,当点值中的点都为 w n w_n wn的幂次时,可以使用 F F T − 1 FFT^{-1} FFT−1来进行计算,将上述方法记作 N T T − 1 ( f ) NTT^{-1}(f) NTT−1(f)
注:关于 w n w_n wn的选择
根据 w n w_n wn的定义,要求 w n 0 w_n^{0} wn0, w n 1 w_n^{1} wn1… w n n − 1 w_n^{n-1} wnn−1互不相同且 w n n = 1 w_n^{n}=1 wnn=1,当f(x)的数值需要mod N时,则需要找到 w n n w_n^{n} wnn同余1模上N。

FFT算法实现
P3803 【多项式乘法FFT】
#include<iostream>
#include<cmath>
using namespace std;
#define NMAX 10000007
int n, m;
int rev[NMAX];
struct complex {//复数类double x, y;//x+y*i的格式complex(double xx = 0, double yy = 0) {x = xx;y = yy;}complex operator + (const complex b) {return complex(x + b.x, y + b.y);}complex operator - (const complex b) {return complex(x - b.x, y - b.y);}complex operator * (const complex b) {return complex(x*b.x-y*b.y, x*b.y + y*b.x);}
};
struct complex f[NMAX], g[NMAX];//需要在复数域上进行计算
struct complex Wn(int n,int type) {//n代表的是等分的分数,type为1代表返回Wn,type为-1代表返回Wn^(-1)double Pi = acos(-1.0);return complex(cos(2 * Pi / n), type * sin(2 * Pi / n));};
void test_for_complex() {complex a = complex(1, 1);complex b = complex(2, 2);printf("%f+i*%f\n", a.x, a.y);printf("%f+i*%f\n", b.x, b.y);complex c = a + b;printf("%f+i*%f\n", c.x, c.y);c = a - b;printf("%f+i*%f\n", c.x, c.y);c = a * b;printf("%f+i*%f\n", c.x, c.y);
}
void FFT(complex *a,int deg,int deg_len,int type) {//1.进行比特反转for (int i = 0; i < deg; i++)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (deg_len - 1));//for (int i = 0; i < deg; i++) cout << rev[i] << " ";for (int i = 0; i < deg; i++) {if(i<rev[i]) swap(a[i],a[rev[i]]);//注意这里只能交换一次}//2.进行迭代计算for (int m = 2; m <= deg; m <<= 1) {//m代表的是合并后的个数//2.1获取原根struct complex wn = Wn(m, type);for (int k = 0; k < deg; k += m) {//k代表的是待处理组(a[k...k+m-1])的第一个位置//2.2对于每一组a[k...k+m/2-1]+a[k+m/2...k+m-1]=a[k...k+m-1]complex w = complex(1, 0);for (int j = 0; j < m / 2; j++) {//k+j指向a[k...k+m/2-1]complex t = w * a[k + j + m / 2];complex u = a[k + j];a[k + j] = t + u;a[k + j + m / 2] = u - t;w = wn * w;}}}}
int main() {cin >> n >> m;for (int i = 0; i < n+1; i++) cin >> f[i].x;for (int j = 0; j < m+1; j++) cin >> g[j].x;//确定等分的分数(由于需要进行加速,所以分数应为2^n的形式)int num = 1, len = 0;while (num < (n + m+1)) {num <<= 1;len++;}FFT(f, num, len, 1);FFT(g, num, len, 1);for (int i = 0; i < num; i++) {f[i] = f[i] * g[i];}FFT(f, num,len, -1);for (int i = 0; i < n + m + 1; i++) cout << int(f[i].x/num + 0.5) << " ";
}
多项式卷积计算
#include<iostream>
#include<cmath>
#include<string>
#include<string.h>
using namespace std;
#define NMAX 102
int n, m;
int rev[NMAX];
struct complex {//复数类double x, y;//x+y*i的格式complex(double xx = 0, double yy = 0) {x = xx;y = yy;}complex operator + (const complex b) {return complex(x + b.x, y + b.y);}complex operator - (const complex b) {return complex(x - b.x, y - b.y);}complex operator * (const complex b) {return complex(x*b.x-y*b.y, x*b.y + y*b.x);}
};
//struct complex f[NMAX], g[NMAX];//需要在复数域上进行计算
struct complex Wn(int n,int type) {//n代表的是等分的分数,type为1代表返回Wn,type为-1代表返回Wn^(-1)double Pi = acos(-1.0);return complex(cos(2 * Pi / n), type * sin(2 * Pi / n));};
void test_for_complex() {complex a = complex(1, 1);complex b = complex(2, 2);printf("%f+i*%f\n", a.x, a.y);printf("%f+i*%f\n", b.x, b.y);complex c = a + b;printf("%f+i*%f\n", c.x, c.y);c = a - b;printf("%f+i*%f\n", c.x, c.y);c = a * b;printf("%f+i*%f\n", c.x, c.y);
}
void FFT(complex *a,int deg,int deg_len,int type) {//1.进行比特反转for (int i = 0; i < deg; i++)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (deg_len - 1));//for (int i = 0; i < deg; i++) cout << rev[i] << " ";for (int i = 0; i < deg; i++) {if(i<rev[i]) swap(a[i],a[rev[i]]);//注意这里只能交换一次}//2.进行迭代计算for (int m = 2; m <= deg; m <<= 1) {//m代表的是合并后的个数//2.1获取原根struct complex wn = Wn(m, type);for (int k = 0; k < deg; k += m) {//k代表的是待处理组(a[k...k+m-1])的第一个位置//2.2对于每一组a[k...k+m/2-1]+a[k+m/2...k+m-1]=a[k...k+m-1]complex w = complex(1, 0);for (int j = 0; j < m / 2; j++) {//k+j指向a[k...k+m/2-1]complex t = w * a[k + j + m / 2];complex u = a[k + j];a[k + j] = t + u;a[k + j + m / 2] = u - t;w = wn * w;}}}}void FFT_new(complex* a, int deg, int deg_len, int type) {//1.进行比特反转for (int i = 0; i < deg; i++)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (deg_len - 1));//for (int i = 0; i < deg; i++) cout << rev[i] << " ";for (int i = 0; i < deg; i++) {if (i < rev[i]) swap(a[i], a[rev[i]]);//注意这里只能交换一次}//迭代计算for (int m = 2; m <= deg; m <<=1) {complex wn = Wn(m, type);//若为逆FTT,则为wn^(-1)for (int j = 0; j < deg; j += m) {//处理a[j...j+m-1]complex w = complex(1, 0);for (int k = 0; k < m / 2; k++) {//框定左侧为a[j...j+m/2-1],由j+k游标指向complex t = w * a[j + k + m / 2];//旋转因子a[j + k + m / 2] = a[j + k] - t;a[j + k] = a[j + k] + t;w = wn * w;}}}//逆FTT需要乘上1/nif (type == -1) {for (int i = 0; i < deg; i++) a[i].x = int(a[i].x / deg + 0.5);}
}
int read(string input, complex * f,int start, int end) {//从string[start...end]中剥离出多项式系数int deg = 0;while(input[start] != '(') start++;//过滤掉不必要的空格使得从左括号开始double coe = 0, exp = 0;for (int i = start+1; i <= end; i++) {if (input[i] == ' ') continue;//遇到空格则直接跳过else if (input[i] == '+' || input[i] == ')') {//cout << coe << " " << exp << endl;f[int(exp)].x = coe;if (exp > deg) deg = int(exp);coe = 0, exp = 0;}else if (input[i] == 'a') {//注意可能存在系数为1的情况if (coe == 0) coe = 1;i+=2;//跳过^while (input[i] != '+' && input[i] != ')') {exp = exp * 10 + input[i++] - '0';}i--;}else coe = coe * 10 + input[i] - '0';}return deg + 1;
}
void output(complex* f,int deg) {for (int i = deg; i >= 0; i--) {if (f[i].x > 0) {if (i == 0) cout << int(f[i].x);else if (int(f[i].x) != 1)cout << int(f[i].x) << "a^" << i;else cout << "a^" << i;if (i == 0)cout << endl;else cout << "+";}}
}
int main() {string input;while (getline(cin, input)) {struct complex f[NMAX], g[NMAX];//需要在复数域上进行计算int pos =input.find('*');//根据题意,多项式的乘法仅仅只含两项int len = strlen(input.c_str());if (!(pos < len && pos >= 0)) {cout << input << endl;//不含*,则直接输出continue;}int deg_f = read(input, f,0,pos-1);int deg_g = read(input, g,pos+1,len-1);int deg = 1, deg_len = 0;while (deg < (deg_f + deg_g)) deg <<= 1, deg_len++;FFT_new(f, deg, deg_len, 1);FFT_new(g, deg, deg_len, 1);for (int i = 0; i < deg; i++) f[i] = f[i] * g[i];FFT_new(f, deg, deg_len, -1);output(f,deg);}
}
NTT算法实现
void NTT(int* a, int n, int x) {//参数设置:a代表待处理的数组,n为度,x代表的是是否是逆NTTint len = 0, cn = n;while (cn) {len++;cn >>= 1;}len--;for (RI i = 1; i < n; ++i) {rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));//cout <<" " << i << " "<< rev[i] << endl;}//首先进行比特反转拷贝for (RI i = 0; i < n; ++i) if (i < rev[i]) swap(a[i], a[rev[i]]);for (RI i = 1; i < n; i <<= 1) {//对于每一层RI gn = ksm(G, (mod - 1) / (i << 1)); //代表的是旋转因子for (RI j = 0; j < n; j += (i << 1)) { //以j到j+(i<<1)为一组,计算j开始的位置RI t1, t2, g = 1;for (RI k = 0; k < i; ++k, g = 1LL * g * gn % mod) {t1 = a[j + k], t2 = 1LL * g * a[j + k + i] % mod; //数组a是如何处理得到的a[j + k] = (t1 + t2) % mod, a[j + k + i] = (t1 - t2 + mod) % mod;}}}if (x == 1) return;int ny = ksm(n, mod - 2);//计算得到n^(-1)reverse(a + 1, a + n); //翻转[1...n-1]位,原因在于,求逆代入的是w^0,w^(-1),w^(-2),...w^(-n+1)// w^0,w^(n-1),w(n-2),...w^1//而此次计算代入的是w^0,w^1,w^2,...w^(n-1),因此进行反转即可for (RI i = 0; i < n; ++i) a[i] = 1LL * a[i] * ny % mod;
}
2.计算多项式的乘法
问题概述:
计算 C ( x ) = A ( x ) ∗ B ( x ) C(x)=A(x)*B(x) C(x)=A(x)∗B(x)
解决方法1
直接按照手算的方式,展开计算,示例代码如下所示。假设A和B的度为n,则时间复杂度为 O ( n 2 ) O(n^2) O(n2)
a=[1,9]
b=[1,6]
c=[0]*(len(a)+len(b))
mod = 998244353
for i in range(len(a)):for j in range(len(b)):c[i+j] =(c[i+j] + a[i]*b[j]) % mod
for i in range(len(c)):print(c[i])
#print(1)
解决办法2
- 首先估算 C ( x ) C(x) C(x)的度为 d e g c deg_c degc
- 计算得到 d e g deg deg,使得 d e g = 2 i deg=2^i deg=2i,且 d e g > d e g c deg>deg_c deg>degc
- 计算向量 a = N T T ( A , d e g ) a=NTT(A,deg) a=NTT(A,deg),向量 b = N T T ( B , d e g ) b=NTT(B,deg) b=NTT(B,deg)
- 计算向量 c = a ∗ b c=a*b c=a∗b
- 向量 C = N T T − 1 ( c , d e g ) C=NTT^{-1}(c,deg) C=NTT−1(c,deg)对应了 C ( x ) C(x) C(x)的各个系数
主体思想:
由于 C ( x ) C(x) C(x)的度为 d e g c deg_c degc,因此至少需要 d e g c deg_c degc个点值来推算 C ( x ) C(x) C(x)的系数,因此需要在 A ( x ) A(x) A(x)和 B ( x ) B(x) B(x)上至少取 d e g c deg_c degc个点值。由于NTT要求 d e g deg deg为 2 n 2^n 2n,因此需要进行第1步和第2步。
#include<iostream>
using namespace std;
int read() {int q = 0; char ch = ' ';while (ch < '0' || ch>'9') ch = getchar();while (ch >= '0' && ch <= '9') q = q * 10 + ch - '0', ch = getchar();return q;
}
#define RI register int
const int mod = 998244353, G = 3, N = 2100000;
int n;
int a[N], b[N], c[N], rev[N];
//根据小费马定理,a^(p-1) 同余 1 mod p (p为素数) a^(p-1)=a*a^(p-2),因此a^(-1) = a^(p-2),使用快速幂来计算a^(p-2)
int ksm(int x, int y) {//快速幂,计算x^yint re = 1;for (; y; y >>= 1, x = 1LL * x * x % mod) {if (y & 1) re = 1LL * re * x % mod;}return re;
}
void NTT(int* a, int n, int x) {//Q:为什么这里仅仅只是考虑了模式的度,而不考虑模式的具体公式//参数设置:a代表待检测的数组,n为度,x代表的是是否是逆NTTint len = 0, cn = n;while (cn) {len++;cn >>= 1;}len--;for (RI i = 1; i < n; ++i) {rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));//cout <<" " << i << " "<< rev[i] << endl;}//首先进行比特反转拷贝for (RI i = 0; i < n; ++i) if (i < rev[i]) swap(a[i], a[rev[i]]);for (RI i = 1; i < n; i <<= 1) {//对于每一层RI gn = ksm(G, (mod - 1) / (i << 1)); //代表的是旋转因子for (RI j = 0; j < n; j += (i << 1)) { //以j到j+(i<<1)为一组,计算j开始的位置RI t1, t2, g = 1;for (RI k = 0; k < i; ++k, g = 1LL * g * gn % mod) {t1 = a[j + k], t2 = 1LL * g * a[j + k + i] % mod; //数组a是如何处理得到的a[j + k] = (t1 + t2) % mod, a[j + k + i] = (t1 - t2 + mod) % mod;}}}if (x == 1) return;int ny = ksm(n, mod - 2);//计算得到n^(-1)reverse(a + 1, a + n); //翻转[1...n-1]位,原因在于,求逆代入的是w^0,w^(-1),w^(-2),...w^(-n+1)// w^0,w^(n-1),w(n-2),...w^1//而此次计算代入的是w^0,w^1,w^2,...w^(n-1),因此进行反转即可for (RI i = 0; i < n; ++i) a[i] = 1LL * a[i] * ny % mod;
}void test_for_ntt() {//使用NTT计算一般的多项式乘法的注意点://1.首先需要估计结果的度,即为所有式子度之和,//2.NTT的度要求为2^n,因此需要找到最小的数,满足2^n的形式,同时需要大于估计的结果的度//3.NTT计算一般多项式乘的过程为,首先计算对于不同的函数,orz个不同的变量对应的值//然后按照计算公式计算得到对应的结果多项式在orz个不同的变量处的取值//最后逆NTT变换,得到结果多项式的系数int a[20] = { 1, 9};NTT(a, 2, 1);NTT(a, 2, -1);int b[20] = { 1, 6};NTT(b, 2, 1);NTT(b, 2, -1);int c[20];int deg = 4; //NTT中只能使用2^n来进行使用NTT(a, deg, 1);NTT(b, deg, 1);for (int i = 0; i < deg; i++) {c[i] = 1LL * a[i] * b[i] % mod;}NTT(c, deg, -1);for (int i = 0; i < deg; i++) {cout << c[i] << endl;}
}
int main()
{test_for_ntt();
}
例题
多项式乘法逆


注:公式推导过程链接
整体思路为:
为了计算mod x d e g x^{deg} xdeg,先计算 mod x ( d e g + 1 ) / 2 x^{(deg+1)/2} x(deg+1)/2,然后利用公式计算mod x d e g x^deg xdeg。具体来说,若deg为奇数,则计算 m o d x ( d e g + 1 ) / 2 mod x^{(deg+1)/2} modx(deg+1)/2 ,利用公式计算得到 mod x d e g + 1 x^{deg+1} xdeg+1的逆,又因为当a≡b mod x n x^n xn 且n>m时,a≡b mod x m x^m xm,则计算结果等于模 x d e g x^{deg} xdeg的逆;若deg为偶数,则计算mod x d e g / 2 x^{deg/2} xdeg/2,利用公式计算得到mod x d e g x^{deg} xdeg
#include<iostream>
using namespace std;
int read() {int q = 0; char ch = ' ';while (ch < '0' || ch>'9') ch = getchar();while (ch >= '0' && ch <= '9') q = q * 10 + ch - '0', ch = getchar();return q;
}
#define RI register int
const int mod = 998244353, G = 3, N = 2100000;
int n;
int a[N], b[N], c[N], rev[N];
//根据小费马定理,a^(p-1) 同余 1 mod p (p为素数) a^(p-1)=a*a^(p-2),因此a^(-1) = a^(p-2),使用快速幂来计算a^(p-2)
int ksm(int x, int y) {//快速幂,计算x^yint re = 1;for (; y; y >>= 1, x = 1LL * x * x % mod) {if (y & 1) re = 1LL * re * x % mod;}return re;
}
void NTT(int* a, int n, int x) {//Q:为什么这里仅仅只是考虑了模式的度,而不考虑模式的具体公式//参数设置:a代表待检测的数组,n为度,x代表的是是否是逆NTTint len = 0, cn = n;while (cn) {len++;cn >>= 1;}len--;for (RI i = 1; i < n; ++i) {rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));//cout <<" " << i << " "<< rev[i] << endl;}//首先进行比特反转拷贝for (RI i = 0; i < n; ++i) if (i < rev[i]) swap(a[i], a[rev[i]]);for (RI i = 1; i < n; i <<= 1) {//对于每一层RI gn = ksm(G, (mod - 1) / (i << 1)); //代表的是旋转因子for (RI j = 0; j < n; j += (i << 1)) { //以j到j+(i<<1)为一组,计算j开始的位置RI t1, t2, g = 1;for (RI k = 0; k < i; ++k, g = 1LL * g * gn % mod) {t1 = a[j + k], t2 = 1LL * g * a[j + k + i] % mod; //数组a是如何处理得到的a[j + k] = (t1 + t2) % mod, a[j + k + i] = (t1 - t2 + mod) % mod;}}}if (x == 1) return;int ny = ksm(n, mod - 2);//计算得到n^(-1)reverse(a + 1, a + n); //翻转[1...n-1]位,原因在于,求逆代入的是w^0,w^(-1),w^(-2),...w^(-n+1)// w^0,w^(n-1),w(n-2),...w^1//而此次计算代入的是w^0,w^1,w^2,...w^(n-1),因此进行反转即可for (RI i = 0; i < n; ++i) a[i] = 1LL * a[i] * ny % mod;
}
void work(int deg, int* a, int* b) {//为了计算mod x^deg,先计算 mod x^((deg+1)/2),然后利用公式计算mod x^deg //若deg为奇数,则计算mod x^((deg+1)/2) ,利用公式计算得到 mod x^(deg+1),又因为a==b mod x^n -> a==b mod x^m (n>m) ,则计算结果是可以适用于x^deg的//若deg为偶数,则计算mod x^(deg/2),利用公式计算得到mod x^deg//公式的计算过程如下(整个计算过程不涉及mod x^n,而是利用NTT计算得到一般的多项式乘法)//使用NTT计算一般的多项式乘法的注意点://1.首先需要估计结果的度,即为所有式子度之和,此处的估计结果为2*deg,即deg<<1//2.NTT的度要求为2^n,因此需要找到最小的数,满足2^n的形式,同时需要大于估计的结果的度,此处为orz//3.NTT计算一般多项式乘的过程为,首先计算对于不同的函数,orz个不同的变量对应的值,即NTT(c, orz, 1), NTT(b, orz, 1);//然后按照计算公式计算得到对应的结果多项式在orz个不同的变量处的取值//最后逆NTT变换,得到结果多项式的系数,此处NTT(b, orz, -1);if (deg == 1) { b[0] = ksm(a[0], mod - 2); return; }work((deg + 1) >> 1, a, b);//这里为什么一定要加上1 a==b mod x^n -> a==b mod x^m (n>m)//处理度,取orz为大于2*deg的最小2^nRI len = 0, orz = 1;while (orz < (deg << 1)) orz <<= 1, ++len;cout << deg << " " << orz << endl;for (RI i = 1; i < orz; ++i) {rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));//cout <<" " << i << " "<< rev[i] << endl;}//将数组a复制到数组c,即c同于a mod x^degfor (RI i = 0; i < deg; ++i) c[i] = a[i];for (RI i = deg; i < orz; ++i) c[i] = 0;NTT(c, orz, 1), NTT(b, orz, 1);for (RI i = 0; i < orz; ++i)b[i] = 1LL * (2 - 1LL * c[i] * b[i] % mod + mod) % mod * b[i] % mod; //算数运算符% * /的优先级是一样的,从左到右计算即可NTT(b, orz, -1);//输出普通的多项式乘法for (RI i = 0; i < orz; ++i) printf("%d,", b[i]);cout << endl;//进行模x^deg处理for (RI i = deg; i < orz; ++i) b[i] = 0; //计算得到b mod x^degfor (RI i = 0; i < orz; ++i) printf("%d,", b[i]);cout << endl;
}
void test_for_ntt() {//使用NTT计算一般的多项式乘法的注意点://1.首先需要估计结果的度,即为所有式子度之和,//2.NTT的度要求为2^n,因此需要找到最小的数,满足2^n的形式,同时需要大于估计的结果的度//3.NTT计算一般多项式乘的过程为,首先计算对于不同的函数,orz个不同的变量对应的值//然后按照计算公式计算得到对应的结果多项式在orz个不同的变量处的取值//最后逆NTT变换,得到结果多项式的系数int a[20] = { 1, 9};NTT(a, 2, 1);NTT(a, 2, -1);int b[20] = { 1, 6};NTT(b, 2, 1);NTT(b, 2, -1);int c[20];int deg = 4; //NTT中只能使用2^n来进行使用NTT(a, deg, 1);NTT(b, deg, 1);for (int i = 0; i < deg; i++) {c[i] = 1LL * a[i] * b[i] % mod;}NTT(c, deg, -1);for (int i = 0; i < deg; i++) {cout << c[i] << endl;}
}
int main()
{//test_for_ntt();//cout << 3 % 5 * 2 << endl;n = read();for (RI i = 0; i < n; ++i) a[i] = read();work(n, a, b);for (RI i = 0; i < n; ++i) printf("%d ", b[i]);return 0;
}
3.循环卷积
#include<iostream>
#include<cmath>
#define NMAX 2000
using namespace std;
int rev[NMAX];int n, m;struct complex {double x, y;//x+y*icomplex(double xx = 0, double yy = 0) { x = xx, y = yy; }//构造函数complex operator +(const complex b) {return complex(x + b.x, y + b.y);}complex operator -(const complex b) {return complex(x - b.x, y - b.y);}complex operator *(const complex b) {return complex(x * b.x - y * b.y, x * b.y + y * b.x);}
}f[NMAX],g[NMAX];
struct complex Wn(int n,int type) {double Pi = acos(-1.0);return complex(cos(2 * Pi / n), type*sin(2 * Pi / n));
}
void FFT(struct complex* f, int deg, int deg_len,int type) {//ftt的逆直接取Wn^(-1)//首先进行比特反转for (int i = 0; i < deg; i++) {rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (deg_len - 1));}for (int i = 0; i < deg; i++) {if (i < rev[i]) swap(f[i], f[rev[i]]);}//迭代进行计算for (int gap = 2; gap <= deg; gap <<= 1) {complex w = Wn(gap,type);for (int g_start = 0; g_start < deg; g_start += gap) {complex x = complex(1, 0);for (int start = g_start; start < g_start + gap / 2; start++) {complex u = f[start], v = f[start + gap / 2] * x;f[start] = u + v;f[start + gap / 2] = u - v;x = x * w;}}}if (type == -1) {for (int i = 0; i < deg; i++) {f[i].x = f[i].x/ deg;}}
}
class NTT {int a[NMAX] = { 1,9 }, b[NMAX] = { 1,6 };int rev[NMAX] = {0};int mod = 998244353;//模数int g = 3;//mod简化剩余系上的生成元int ksm(int a, int b, int mod) {int ret = 1;while (b) {if (b & 1) ret = ((long long )ret) * a % mod;a = ((long long )a) * a % mod;b >>= 1;}return ret;}void ntt(int* f, int deg, int deg_len, int type) {//首先进行比特反转for (int i = 0; i < deg; i++) {rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (deg_len - 1));}for (int i = 0; i < deg; i++) {if (i < rev[i]) swap(f[i], f[rev[i]]);}//迭代进行计算for (int gap = 2; gap <= deg; gap <<= 1) {int w = ksm(g, (mod - 1) / gap, mod);for (int g_start = 0; g_start < deg; g_start += gap) {int x = 1;for (int start = g_start; start < g_start + gap / 2; start++) {int u = f[start], v = (1LL * f[start + gap / 2] * x) % mod;f[start] = (u + v)% mod;f[start + gap / 2] = (u - v + mod) % mod;//做减法要加上mod来避免负数出现x = (1LL* x * w) % mod;}}}//求逆运算处理if (type == -1) {for (int i = 1; i < deg / 2; i++) swap(f[i], f[deg - i]);int inv_deg = ksm(deg, mod - 2, mod);for (int i = 0; i < deg; i++) f[i] = 1LL * f[i] * inv_deg % mod;}//结果输出展示for (int i = 0; i < deg; i++) cout << f[i] << " ";cout << endl;}
public:void test_for_ntt() {ntt(a, 4, 2, 1);ntt(b, 4, 2, 1);for (int i = 0; i < 4; i++) a[i] = (1LL *a[i] * b[i]) % mod;ntt(a, 4, 2, -1);for (int i = 0; i < 4; i++) cout << a[i] << " ";}
};void test_for_ftt() {//计算最高次数分别为n和m的多项式f(x)和g(x)的卷积cin >> n >> m;for (int i = 0; i < n + 1; i++) cin >> f[i].x;for (int j = 0; j < m + 1; j++) cin >> g[j].x;//确定等分的分数(由于需要进行加速,所以分数应为2^n的形式)int num = 1, len = 0;while (num < (n + m + 1)) {num <<= 1;len++;}FFT(f, num, len, 1);FFT(g, num, len, 1);for (int i = 0; i < num; i++) {//cout << f[i].x << " " << g[i].x << endl;f[i] = f[i] * g[i];}FFT(f, num, len, -1);for (int i = 0; i < n + m + 1; i++) cout << int(f[i].x + 0.5) << " ";
}
int main() {NTT t;t.test_for_ntt();
}
相关文章:

NTT功能与实现
NTT的基础功用与拓展功能: 1.evaluate和interpolate evaluate的本质是选择n个点(假设f(x)的度为n),计算得到其值,因此根据定义可以直接进行代入计算。为了加快计算的过程选取 w n w_n wn的幂次(DFT问题即离散傅里叶变换),使用FFT算法来加…...
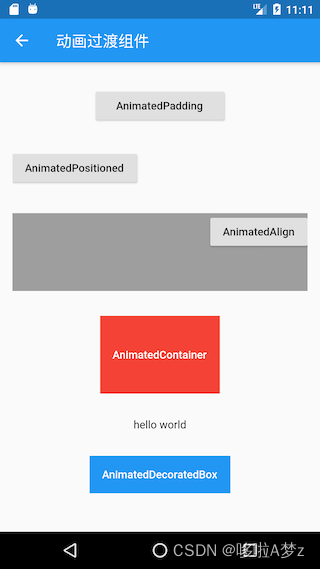
Flutter(九)Flutter动画和自定义组件
目录 1.动画简介2.动画实现和监听3. 自定义路由切换动画4. Hero动画5.交织动画6.动画切换7.Flutter预置的动画过渡组件自定义组件1.简介2.组合组件3.CustomPaint 和 RenderObject 1.动画简介 Animation、Curve、Controller、Tween这四个角色,它们一起配合来完成一个…...

【python】可视化
柱状图 matplotlib之pyplot模块之柱状图(bar():基础参数、外观参数)_plt.bar_mighty13的博客-CSDN博客 bar()的基础参数如下: x:柱子在x轴上的坐标。浮点数或类数组结构。注意x可以为字符串数组! height&…...

C++继承多接口,调用虚函数跳转到错误接口的虚函数的奇怪问题
问题重现 定义了两个接口IA IB class IA{public:virtual void funA() = 0; }; class IB{public:virtual void funB() = 0; }...

C++:日期类
学习目标: 加深对四个默认构造函数的理解: 1.构造函数 2.析构函数 3.拷贝构造 4.运算符重载 实现功能 1.比较日期的大小 2.日期-天数 3.前/后置,-- 这里基本会使用运算符重载 定义一个日期类 class Date { public://1.全缺省参数的构造函数Da…...

c++ 学习之 构造函数的使用
上代码 class person { public:person(){cout << " person 的无参默认构造函数 " << endl;}person(int age){cout << " person 的有参默认构造函数 " << endl;m_age age;}person(const person& other){cout << "…...

算法通关村15关 | 超大规模数据场景常见问题
1.用4KB内存寻找重复元素 题目:给定一个数组,包含从1到N的整数,N最大为32000,数组可能还有重复值,且N的取值不定,若只有4KB的内存可用,该如何打印数组中所有重复元素。 分析: 本身是…...

qemu编译与使用
文章目录 1、安装依赖2、下载qemu源码3、编译4、运行5、qemu参数 qemu 是一个硬件虚拟化程序(hypervisor that performs hardware virtualization),与传统的 VMware / VirtualBox 之类的虚拟机不同,它可以通过 binary translation…...
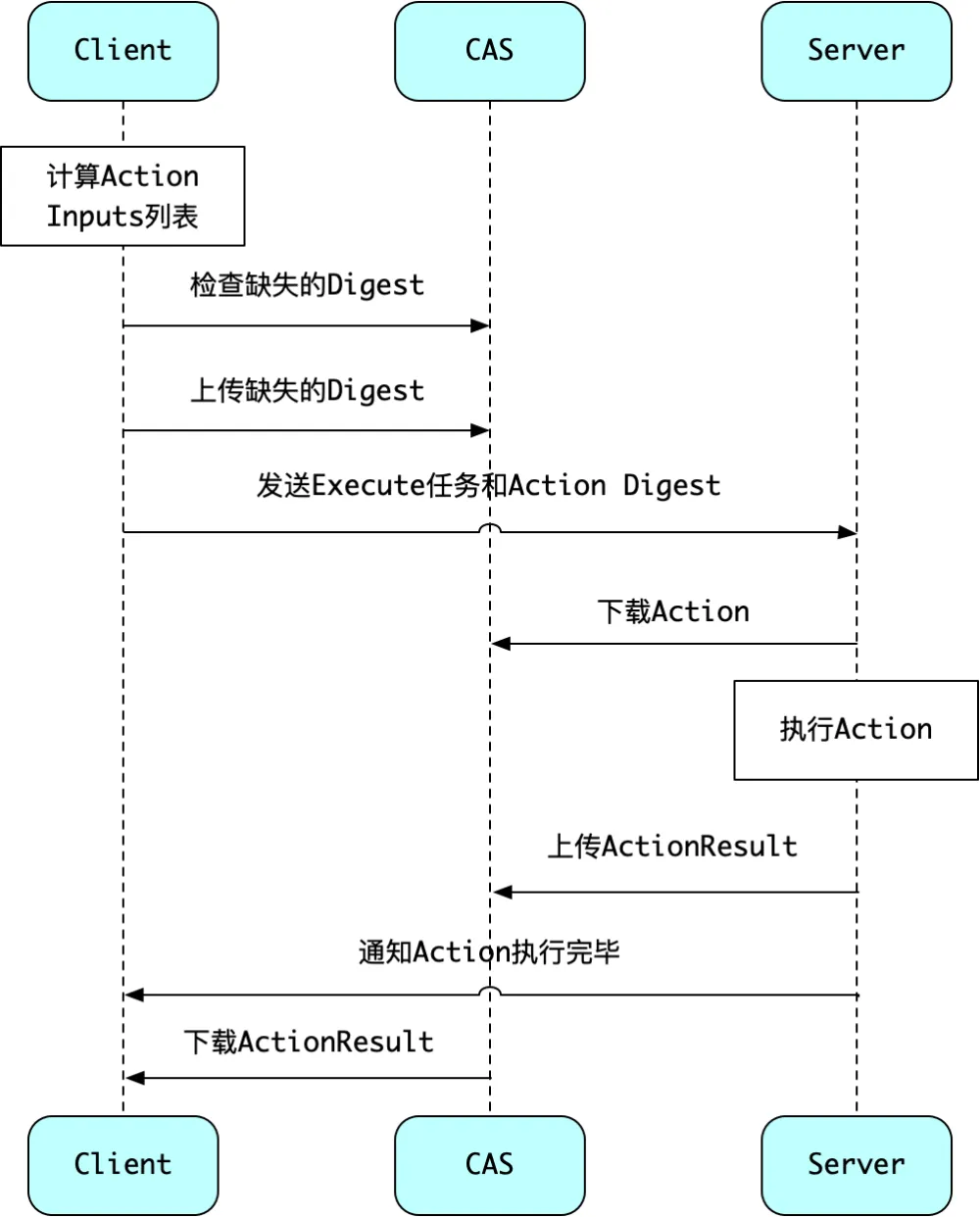
bazel远程构建(Remote Execution)
原理 既然 ActionResult 可以被不同的 Bazel 任务共享,说明 ActionResult 和 Action 在哪里执行并没有关系。因此,Bazel 在构建时,可以把 Action 发送给另一台服务器执行,对方执行完,向 CAS 上传 ActionResult&#x…...
uniapp 微信小程序仿抖音评论区功能,支持展开收起
最近需要写一个评论区功能,所以打算仿照抖音做一个评论功能,支持展开和收起, 首先我们需要对功能做一个拆解,评论区功能,两个模块,一个是发表评论模块,一个是评论展示区。接下来对这两个模块进行…...
js:创建一个基于vite 的React项目
相关文档 Vite 官方中文文档React 中文文档React RouterRedux 中文文档Ant Design 5.0Awesome React 创建vite react项目 pnpm create vite react-app --template react# 根据提示,执行命令 cd react-app pnpm install pnpm run dev项目结构 $ tree -L 1 . ├─…...
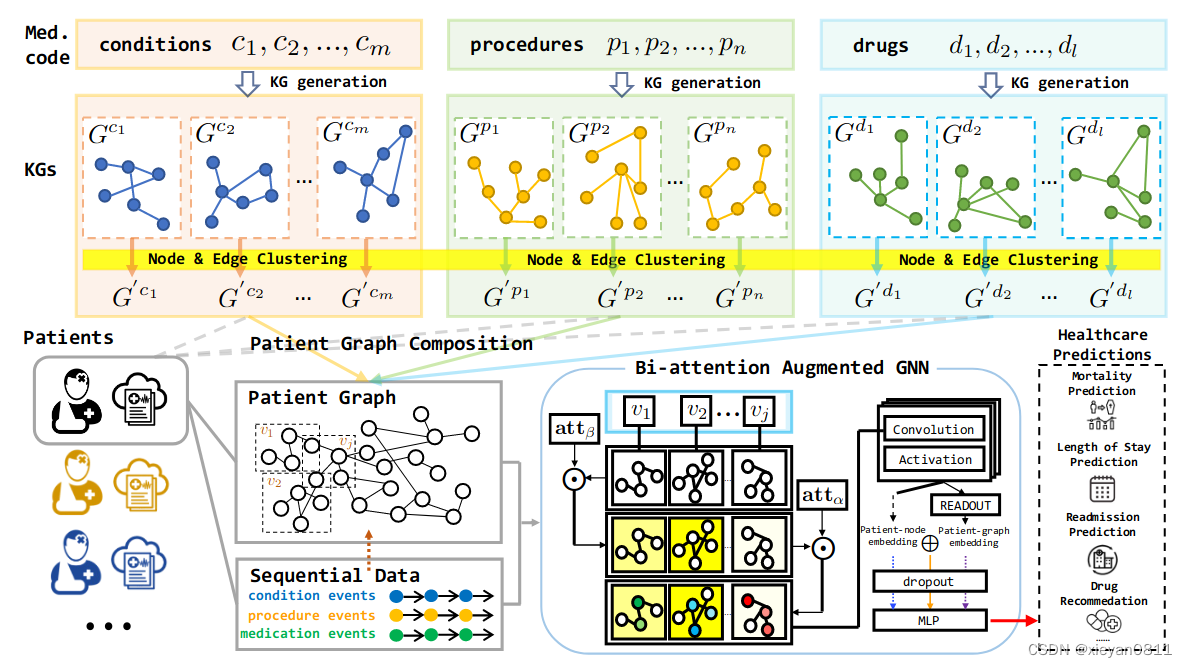
论文阅读_医疗知识图谱_GraphCare
英文名称: GraphCare: Enhancing Healthcare Predictions with Open-World Personalized Knowledge Graphs 中文名称: GraphCare:通过开放世界的个性化知识图增强医疗保健预测 文章: http://arxiv.org/abs/2305.12788 代码: https://github.com/pat-jj/GraphCare 作…...
Android 蓝牙开发( 四 )
前言 上一篇文章给大家分享了Kotlin版的Android蓝牙的基础知识和基础用法,不过上一篇都是一些零散碎片化的程序,,这一篇给大家分享Android蓝牙开发实战项目KotlinCompose的初步使用 效果演示 : Android Compose 蓝牙开发 Android蓝牙实战开发…...

涂鸦智能携手亚马逊云科技 共建“联合安全实验室” 为IoT发展护航
2023年8月31日,全球化IoT开发者平台涂鸦智能(NYSE: TUYA,HKEX: 2391)在“2023亚马逊云科技re:Inforce中国站”大会宣布与全球领先的云计算公司亚马逊云科技共同成立“联合安全实验室”,旨在加强IoT行业的安全合规能力与…...
Oracle21C--Windows卸载与安装
卸载方法: (1)WinR,输入services.msc,打开服务,把Oracle相关的服务全部停止运行(重要) (2)WinR,输入regedit,打开注册表,删除Oracle开…...

关于 MySQL、PostgresSQL、Mariadb 数据库2038千年虫问题
MySQL 测试时间:2023-8 启动MySQL服务后,将系统时间调制2038年01月19日03时14分07秒之后的日期,发现MySQL服务自动停止。 根据最新的MySQL源码(mysql-8.1.0)分析,sql/sql_parse.cc中依然存在2038年千年虫…...

Linux - Docker 安装使用 常用命令 教程
Docker 官方文档地址: Get Started | Docker 中文参考手册: https://docker_practice.gitee.io/zh-cn/ 1.什么是 Docker 1.1 官方定义 最新官网首页 # 1.官方介绍 - We have a complete container solution for you - no matter who you are and where you are on your contain…...

AtCoder Beginner Contest 318 G - Typical Path Problem 题解
G - Typical Path Problem 题目大意 给定一张 N N N 个点、 M M M 条边的简单无向图 G G G 和三个整数 A , B , C A,B,C A,B,C。 是否存在一条从顶点 A A A 到 C C C,且经过 B B B 的简单路径? 数据范围: 3 ≤ N ≤ 2 1 0 5 3\le …...

21.4 CSS 盒子模型
1. 边框样式 border-style属性: 指定元素的边框样式.常用属性值: - none: 无边框(默认值). - solid: 实线边框. - dotted: 点状边框. - dashed: 虚线边框. - double: 双线边框. - groove: 凹槽状边框. - ridge: 脊状边框. - inset: 内阴影边框. - outset: 外阴影边框.这些值可…...
MybatisPlus入门
MybatisPlus入门 1.MyBatis-Plus1.1 ORM介绍1.2 MyBatis-Plus介绍 2.代码链接数据库2.1 创建项目2.2 添加依赖2.3 链接数据库2.3.1 准备数据库2.3.2 链接数据库2.3.3 创建实体类 2.4 创建Mapper层2.5 创建Controller层2.6 浏览器访问测试 MybatisPlus官方网站: 官网…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
