AtCoder Beginner Contest 318 G - Typical Path Problem 题解
G - Typical Path Problem
题目大意
给定一张 N N N 个点、 M M M 条边的简单无向图 G G G 和三个整数 A , B , C A,B,C A,B,C。
是否存在一条从顶点 A A A 到 C C C,且经过 B B B 的简单路径?
数据范围:
- 3 ≤ N ≤ 2 × 1 0 5 3\le N\le 2\times 10^5 3≤N≤2×105
- N − 1 ≤ M ≤ min ( N ( N − 1 ) 2 , 2 × 1 0 5 ) N-1\le M\le \min(\frac{N(N-1)}2,2\times 10^5) N−1≤M≤min(2N(N−1),2×105)
- 1 ≤ A , B , C ≤ N 1\le A,B,C\le N 1≤A,B,C≤N( A , B , C A,B,C A,B,C 互不相同)
什么是 简单路径 ?
简单路径 是不重复经过同一个点的路径。例如, 1 → 2 → 3 1\to 2\to 3 1→2→3 是简单路径,但 1 → 2 → 1 1\to 2\to 1 1→2→1 不是简单路径。
解法1:最大流
不难发现,存在一条 A → B → C A\to B\to C A→B→C 的简单路径,当且仅当存在一条 B → A B\to A B→A 和一条 B → C B\to C B→C 的路径,使得这两条路径不经过同一个点( B B B 除外)。因此,我们可以构建网络流模型来解决此问题。
考虑由 ( 2 N + 2 ) (2N+2) (2N+2) 个点组成的有向图 G ′ G' G′:
- 源点: s s s
- 汇点: t t t
- G G G 中每个点对应的入点: x 1 , … , x N x_1,\dots,x_N x1,…,xN
- G G G 中每个点对应的出点: y 1 , … , y N y_1,\dots,y_N y1,…,yN
然后进行连边:
- 对于每个 1 ≤ i ≤ N 1\le i\le N 1≤i≤N,从入点 x i x_i xi 向出点 y i y_i yi 连接一条流量为 1 1 1 的边;
- 从源点 s s s 到中转点的入点 x B x_B xB 连接一条流量为 2 2 2 的边;
- 从 A A A 和 C C C 的出点 y A , y C y_A,y_C yA,yC 向汇点 t t t 分别连接一条流量为 1 1 1 的边;
- 最后, ∀ ( u , v ) ∈ E G \forall (u,v)\in E_G ∀(u,v)∈EG,连接 y u → x v y_u \to x_v yu→xv 和 y v → x u y_v \to x_u yv→xu,流量为 1 1 1。
计算 s s s 到 t t t 的最大流,如果最大流为 2 2 2 则必定有存在不经过同一个顶点的 B → A , B → C B\to A,B\to C B→A,B→C 的路径。
证明
显然,如果最大流为 2 2 2,必然通过了 y A y_A yA 和 y C y_C yC 向汇点连接的边,则一定分别有 B → A B\to A B→A 和 B → C B\to C B→C 的路径。
假设选择的这两条路径经过了同一顶点 v v v,则两流都必须经过 x v → y v x_v\to y_v xv→yv 这一条流量为 1 1 1 的边,此时最大流不可能超过 1 1 1。而最大流为 2 2 2,说明假设不成立,故没有经过同一顶点。
若使用 Dinic \text{Dinic} Dinic 算法,由于最大流不超过 2 2 2,网络流的时间复杂度为 O ( N + M ) \mathcal O(N+M) O(N+M)。
代码实现
在以下的两种实现中,我们规定
- 源点: s = 0 s=0 s=0
- 汇点: t = 2 n + 1 t=2n+1 t=2n+1
- i i i 的入点: x i = i x_i=i xi=i
- i i i 的出点: y i = n + i y_i=n+i yi=n+i
AC Library 实现
AtCoder Library 内置最大流的 Dinic \text{Dinic} Dinic 实现。
#include <cstdio>
#include <atcoder/maxflow>
using namespace std;int main()
{int n, m, a, b, c;scanf("%d%d%d%d%d", &n, &m, &a, &b, &c);int s = 0, t = (n << 1) + 1;atcoder::mf_graph<int> G(t + 1);G.add_edge(s, b + n, 2);G.add_edge(a + n, t, 1);G.add_edge(c + n, t, 1);for(int i=1; i<=n; i++)G.add_edge(i, i + n, 1);while(m--){int x, y;scanf("%d%d", &x, &y);G.add_edge(x + n, y, 1);G.add_edge(y + n, x, 1);}puts(G.flow(s, t, 2) == 2? "Yes": "No");return 0;
}
Dinic 手写实现
Dinic \text{Dinic} Dinic 算法对于此图的时间复杂度为 O ( N + M ) \mathcal O(N+M) O(N+M)。如果不清楚算法原理可以参考 OI Wiki。
关于空间分配问题
由于新图 G ′ G' G′ 包含 ( N + 2 M + 3 ) (N+2M+3) (N+2M+3) 条边,若使用静态链式前向星存图,数组大小需要开到 2 ( N + 2 M + 3 ) 2(N+2M+3) 2(N+2M+3),其理论最大值为 1.2 × 1 0 6 + 6 1.2\times 10^6+6 1.2×106+6。此处建议使用 1.25 × 1 0 6 1.25\times 10^6 1.25×106 大小的数组。
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#define maxn 400005
#define maxm 1250005
using namespace std;int n, s, t, head[maxn], cur[maxn], dis[maxn],cnt, w[maxm], to[maxm], nxt[maxm];inline void add(int u, int v, int flow)
{nxt[cnt] = head[u];head[u] = cnt;to[cnt] = v;w[cnt++] = flow;
}inline void add_flow(int u, int v, int f)
{add(u, v, f);add(v, u, 0);
}inline bool bfs()
{memset(dis, -1, sizeof(int) * n);dis[s] = 0, cur[s] = head[s];queue<int> q;q.push(s);while(!q.empty()){int v = q.front(); q.pop();for(int i=head[v]; ~i; i=nxt[i])if(w[i]){int u = to[i];if(dis[u] == -1){dis[u] = dis[v] + 1, cur[u] = head[u];if(u == t) return true;q.push(u);}}}return false;
}int dfs(int v, int flow)
{if(v == t) return flow;int res = 0;for(int i=cur[v]; ~i && flow; i=nxt[i]){cur[v] = i;int u = to[i];if(w[i] && dis[u] == dis[v] + 1){int k = dfs(u, min(flow, w[i]));w[i] -= k;w[i ^ 1] += k;flow -= k;res += k;}}return res;
}int main()
{int n, m, a, b, c;scanf("%d%d%d%d%d", &n, &m, &a, &b, &c);s = 0, t = (n << 1) + 1, ::n = t + 1;memset(head, -1, sizeof(int) * ::n);add_flow(s, b + n, 2);add_flow(a + n, t, 1);add_flow(c + n, t, 1);for(int i=1; i<=n; i++)add_flow(i, i + n, 1);while(m--){int x, y;scanf("%d%d", &x, &y);add_flow(x + n, y, 1);add_flow(y + n, x, 1);}int mf = 0;while(bfs()) mf += dfs(s, 2);puts(mf == 2? "Yes": "No");return 0;
}
解法2:圆方树
注意到以下算法的正确性:
- 找到 A → C A\to C A→C 的任意简单路径。对于经过的每一个点双连通分量,如果 B B B 在此点双内,则必然存在 A → B → C A\to B\to C A→B→C 的简单路径;如果 B B B 不属于任一经过的点双,则不可能存在 A → B → C A\to B\to C A→B→C 的简单路径。
因此,可以使用 Tarjan \text{Tarjan} Tarjan 算法构造原图的圆方树 T T T 来解决此问题。将上述算法转换到圆方树上如下:
- 在 T T T 上找到 A → C A\to C A→C 的唯一简单路径。对于经过的每一个方点,如果 B B B 是与其相邻的圆点,则必然存在 A → B → C A\to B\to C A→B→C 的简单路径;如果 B B B 不与任一经过的方点相邻,则不可能存在 A → B → C A\to B\to C A→B→C 的简单路径。
总时间复杂度为 O ( N + M ) \mathcal O(N+M) O(N+M),实际运行时间优于网络流解法。
代码实现
小贴士:圆方树相关的数组要开到两倍大小,不然会 RE 哦~
#include <cstdio>
#include <cstdlib>
#include <vector>
#define maxn 200005
using namespace std;inline void setmin(int& x, int y)
{if(y < x) x = y;
}vector<int> G[maxn], T[maxn << 1];inline void add_edge(vector<int>* G, int x, int y)
{G[x].push_back(y);G[y].push_back(x);
}int dfc, dfn[maxn], low[maxn], top, st[maxn], cnt;void tarjan(int v)
{low[v] = dfn[v] = ++dfc;st[++top] = v;for(int u: G[v])if(!dfn[u]){tarjan(u);setmin(low[v], low[u]);if(low[u] == dfn[v]){add_edge(T, v, ++cnt);do add_edge(T, st[top], cnt);while(st[top--] != u);}}else setmin(low[v], dfn[u]);
}int n, m, a, b, c, ct[maxn << 1];
void dfs(int v, int par)
{if(v > n)for(int u: T[v])ct[u] ++;if(v == c){puts(ct[b]? "Yes": "No");exit(0);}for(int u: T[v])if(u != par)dfs(u, v);if(v > n)for(int u: T[v])ct[u] --;
}int main()
{scanf("%d%d%d%d%d", &n, &m, &a, &b, &c);while(m--){int x, y;scanf("%d%d", &x, &y);add_edge(G, x, y);}cnt = n;tarjan(1);dfs(a, -1);return 0;
}
总结
三种解法的对比参见下表:
| 解法 | 代码长度 | 运行时间 | 内存占用 |
|---|---|---|---|
| 最大流(AC Library)1 | 523 B 523~\mathrm{B} 523 B | 337 m s 337~\mathrm{ms} 337 ms | 106480 K B 106480~\mathrm{KB} 106480 KB |
| 最大流(Dinic)2 | 1650 B 1650~\mathrm{B} 1650 B | 334 m s 334~\mathrm{ms} 334 ms | 46980 K B 46980~\mathrm{KB} 46980 KB |
| 圆方树3 | 1142 B 1142~\mathrm{B} 1142 B | 162 m s 162~\mathrm{ms} 162 ms | 57824 K B 57824~\mathrm{KB} 57824 KB |
可见,圆方树算法的运行速度最快,最大流(AC Library)的代码最短,最大流(Dinic)的内存占用最小。
个人评价
这道题出得很好,题意简单而内涵丰富。
我赛时甚至没想到还可以网络流
https://atcoder.jp/contests/abc318/submissions/45209577 ↩︎
https://atcoder.jp/contests/abc318/submissions/45212257 ↩︎
https://atcoder.jp/contests/abc318/submissions/45210151 ↩︎
相关文章:

AtCoder Beginner Contest 318 G - Typical Path Problem 题解
G - Typical Path Problem 题目大意 给定一张 N N N 个点、 M M M 条边的简单无向图 G G G 和三个整数 A , B , C A,B,C A,B,C。 是否存在一条从顶点 A A A 到 C C C,且经过 B B B 的简单路径? 数据范围: 3 ≤ N ≤ 2 1 0 5 3\le …...

21.4 CSS 盒子模型
1. 边框样式 border-style属性: 指定元素的边框样式.常用属性值: - none: 无边框(默认值). - solid: 实线边框. - dotted: 点状边框. - dashed: 虚线边框. - double: 双线边框. - groove: 凹槽状边框. - ridge: 脊状边框. - inset: 内阴影边框. - outset: 外阴影边框.这些值可…...
MybatisPlus入门
MybatisPlus入门 1.MyBatis-Plus1.1 ORM介绍1.2 MyBatis-Plus介绍 2.代码链接数据库2.1 创建项目2.2 添加依赖2.3 链接数据库2.3.1 准备数据库2.3.2 链接数据库2.3.3 创建实体类 2.4 创建Mapper层2.5 创建Controller层2.6 浏览器访问测试 MybatisPlus官方网站: 官网…...

飞腾平台芯片测试固件(SFW)和开机启动log
一、说两句 最近公司飞腾产品越来越多了,FT-2000/4的D2000的X100的,最近又新出了E2000。越来越多新来的小孩儿开始加入到飞腾的调测试中,那么在他们实际的调试中会遇到很多的问题。在固件启动阶段有的板卡会有一些异常,有时我们需…...

【大数据实训】基于Hive的北京市天气系统分析报告(二)
博主介绍:✌全网粉丝6W,csdn特邀作者、博客专家、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于大数据技术领域和毕业项目实战✌ 🍅文末获取项目联系🍅 目录 1. 引言 1.1 项目背景 1 1.2 项目意义 1 2.…...

WPF列表样式
WPF的数据绑定系统自动生成列表项对象,为单个项应用所需的样式不是很容易。解决方案是ItemContainerStyle 属性。如果设置了ItemContainerStyle 属性,当创建列表项时,列表控件会将其向下传递给每个项。对于ListBox控件,每个项有Li…...
Android逆向学习(二)vscode进行双开与图标修改
Android逆向学习(二)vscode进行双开与图标修改 写在前面 这其实应该还是吾爱的第一个作业,但是写完上一个博客的时候已经比较晚了,如果继续敲机械键盘吵到室友,我怕我看不到明天的太阳,所以我决定分成两篇…...
一个基于YAPI接口生产代码的开源工具
前后端分离的开发模式是一种趋势,但如果缺少好的开发工具跟管理模式,会使得前后端开发人员相互等待,扯皮等问题。从而影响项目的交付进度。 通过实践摸索,YAPI是一款很适合前后端分离开发的协助工具。它以项目为维度,可…...

Redis 缓存穿透击穿和雪崩
一、说明 Redis 缓存的使用,极大的提升了应用程序的性能和效率,特别是数据查询方面。但同时,它也带来了一些问题。其中,最要害的问题,就是数据的一致性问题,从严格意义上讲,这个问题无解。如果对…...
在windows上配置ninja环境
ninja使用并行任务来编译工程,比cmake编译快了一个数量级,是谷歌在2010年为了提高cmake的编译速度而开发一款编译工具。下面介绍在windows上配置ninja环境。 1 下载ninja ninja官网地址: https://github.com/ninja-build/ninja/releases …...
③matlab向量和矩阵
目录 手动输入数组 创建等间距向量 数组创建函数 手动输入数组 1.背景 单个称为标量的数值实际上是一个 11 数组,也即它包含 1 行 1 列。 任务 创建一个名为 x 并且值为 4 的变量。 2.您可以使用方括号创建包含多个元素的数组。 x [3 5] x 3 5 任务 …...
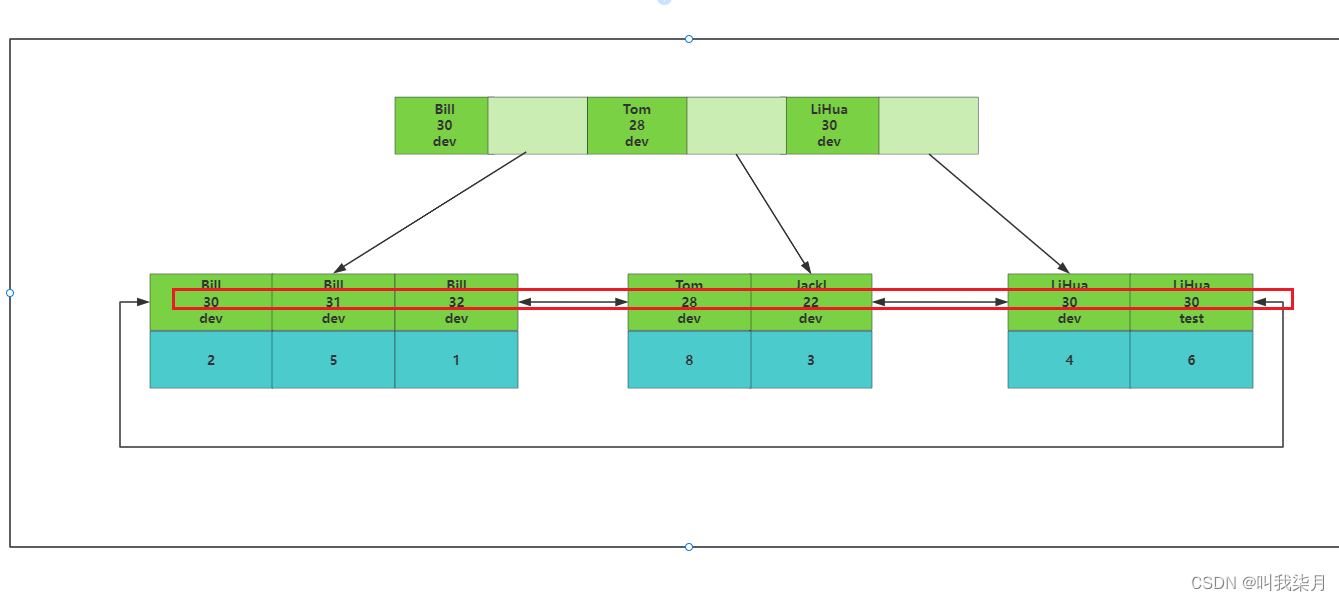
一、了解[mysql]索引底层结构和算法
目录 一、索引1.索引的本质2.mysql的索引结构 二、存储引擎1.MyISAM2.InnoDB3.为什么建议InnoDB表要建立主键并且推荐int类型自增?4.innodb的主键索引和非主键索引(二级索引)区别5.联合索引 一、索引 1.索引的本质 索引:帮助mysql高效获取数…...

DockerFile常用命令
以下是常见的Dockerfile命令: FROM:FROM命令用于指定基础镜像。基础镜像是构建镜像的起点。例如,FROM ubuntu:latest表示使用最新版本的Ubuntu作为基础镜像。 MAINTAINER:MAINTAINER命令用于指定镜像的维护者信息。一般格式为&am…...

Android 动画之插值器PathInterpolator
Android 的View动画、属性动画都可以设置动画插值器,以此来实现不同的动画效果。 这篇文章 Android View动画整理 有介绍各种插值器的效果,这一篇专访 PathInterpolator 。 参考官网 添加曲线动作 , PathInterpolator 基于 贝塞尔曲线 或 …...

递归学习(转载)
转载至 https://www.cnblogs.com/king-lps/p/10748535.html 为避免原文丢失,因此原文转载作者【三年一梦】的帖子 前言 相信不少同学和我一样,在刚学完数据结构后开始刷算法题时,遇到递归的问题总是很头疼,而一看解答,…...

python接口自动化(二)--什么是接口测试、为什么要做接口测试(详解)
简介 上一篇和大家一起科普扫盲接口后,知道什么是接口,接口类型等,对其有了大致了解之后,我们就回到主题-接口测试。 什么是接口测试 接口测试是测试系统组件间接口的一种测试。接口测试主要用于检测外部系统与系统之间以及内部各…...
)
HashMap源码阅读(一)
HashMap继承抽象类AbstractMap,AbstractMap抽象类实现了Map接口 一、HashMap中的静态常量 //默认初始容量 static final int DEFAULT_INITIAL_CAPACITY 1 << 4; // aka 16 //最大长度 static final int MAXIMUM_CAPACITY 1 << 30; //负载因子&#…...

C语言:动态内存(一篇拿捏动态内存!)
目录 学习目标: 为什么存在动态内存分配 动态内存函数: 1. malloc 和 free 2. calloc 3. realloc 常见的动态内存错误: 1. 对NULL指针的解引用操作 2. 对动态开辟空间的越界访问 3. 对非动态开辟内存使用free释放 4. 使用free释…...

Lua - 替换字符串中的特殊字符
//替换指定串 s string.gsub("Lua is good", "good", "bad") print(s) --> Lua is bad//替换特殊字符 a "我们使用$"; b string.gsub(a, "%$", "RMB"); print(b) --> 我们使用RMB//替换反斜杠 path …...

按钮控件之3---QRadioButton 单选按钮/单选框控件
本文详细的介绍了QRadioButton控件的各种操作,例如:QRadioButton分组、默认选中、禁用启用、重置样式等操作。 一、QRadioButton部件提供了一个带有文本标签的单选框(单选按钮)。QRadioButton是一个可以切换选中(chec…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...
