代码随想录算法训练营Day45 | 70. 爬楼梯 (进阶) | 322. 零钱兑换 | 279. 完全平方数
文章目录
- 70. 爬楼梯 (进阶)
- 322. 零钱兑换
- 二维数组
- 滚动数组
- 279. 完全平方数
70. 爬楼梯 (进阶)
题目链接 | 理论基础
以完全背包的思路来解题,正如组合总和 Ⅳ 中提到的一样。在本题中,先背包后物品的思路就显得非常合理明显了。
本题中的物品就是可以行走的步数 [1, 2],重量是 n,可以重复选取步数,求走到第 n 层有多少种走法。这样抽象过后,就和组合总和 Ⅳ 一样是求排列了。
- dp 的下标含义:
dp[j]是到达第 j 层的方法数 - dp 递推公式:
dp[j] += dp[j - i] - dp 数组的初始化:根据递推公式可以得知
dp[0]=1是必须的,也符合前两层的结果,其他的初始化为 0。 - dp 遍历顺序:需要得到排列结果,先背包后物品(在爬楼梯的背景下就很合理)
- 举例推导:省略
class Solution:def climbStairs(self, n: int) -> int:choices = [1, 2]# dp[i] represents the number of ways to reach position idp = [0] * (n+1)dp[0] = 1# dp formulafor j in range(n+1):for i in range(len(choices)):if j >= choices[i]:dp[j] += dp[j-choices[i]]return dp[-1]
本题看上去是个简单的爬楼梯,但实际上是个简单的完全背包,重要的是可以考验对物品和背包的遍历顺序的理解。事实上,以后遇到排列的完全背包问题,以爬楼梯的思路来理解会非常有效!
322. 零钱兑换
题目链接 | 理论基础
本题和 零钱兑换II 非常相似,依然是典型的完全背包问题。区别在于,零钱兑换II 需要组合数,这就规定了滚动数组的遍历顺序;本题只需要最小组合数,而不在乎得到该最小数的方式是组合或是排列。
二维数组
-
dp 数组的下标含义:
dp[i][j],使用硬币 [0, i] 组成金额j所使用的最小硬币数 -
dp 递推公式:
dp[i][j] = min(dp[i-1][j], dp[i-1][j-coins[i]] + 1) -
dp 的初始化:本题的大坑!
- 二维数组的初始化中 ,
coins[0](i=0)和 j=0 的情况是比较容易想到的:- 只能使用一个硬币时,只有该硬币面值的整数倍金额 j 会初始化为
j // coins[0] - 当金额为 0 的时候,不管有多少硬币可以使用,都只需要 0 个硬币即可达成金额 0
- 只能使用一个硬币时,只有该硬币面值的整数倍金额 j 会初始化为
- 那些不需要特殊初始化的位置才是需要小心的!
- 由于题目要求“无法构成金额的情况返回 -1”,自然想到应该优先把所有值初始化为 -1。这么做就会有下面第一种复杂的解法,要考虑
min()中每个元素为 -1 的情况,堪称崩溃。 - 由于
min()的特性,最好的初始化应该是float('inf'),这样不会影响后续的递推,也不会影响初始化,只需要在最后检查结果是否是float('inf')即可。 - 如果被题目默认的初始化条件所迷惑,而没有认识到
min()的需求,那就会踩坑(虽然也能解决问题)。
- 由于题目要求“无法构成金额的情况返回 -1”,自然想到应该优先把所有值初始化为 -1。这么做就会有下面第一种复杂的解法,要考虑
- 二维数组的初始化中 ,
-
dp 的遍历顺序:由于不需要排列,二维数组可以解决,物品和背包的顺序无所谓。
-
举例推导:
coins = [1, 2, 5], amount = 50 1 2 3 4 5 1 0 1 2 3 4 5 2 0 1 1 2 2 3 5 0 1 1 2 2 1
class Solution:def coinChange(self, coins: List[int], amount: int) -> int:# dp[i][j] represents the smallest number to make j using coins [0, i]dp = [[-1] * (amount + 1) for _ in range(len(coins))]for j in range(amount + 1):if j % coins[0] == 0:dp[0][j] = j // coins[0]for i in range(len(coins)):dp[i][0] = 0# dp formulafor i in range(1, len(coins)):for j in range(amount + 1):if j < coins[i]:dp[i][j] = dp[i-1][j]else:if dp[i-1][j] >= 0 and dp[i][j-coins[i]] >= 0:dp[i][j] = min(dp[i-1][j], dp[i][j-coins[i]] + 1)elif dp[i-1][j] == -1 and dp[i][j-coins[i]] >= 0:dp[i][j] = dp[i][j-coins[i]] + 1elif dp[i-1][j] >= 0 and dp[i][j-coins[i]] == -1:dp[i][j] = dp[i-1][j]else:dp[i][j] = -1return dp[-1][-1]
正确初始化的解法
class Solution:def coinChange(self, coins: List[int], amount: int) -> int:# dp[i][j] represents the smallest number to make j using coins [0, i]dp = [[float('inf')] * (amount + 1) for _ in range(len(coins))]for j in range(amount + 1):if j % coins[0] == 0:dp[0][j] = j // coins[0]for i in range(len(coins)):dp[i][0] = 0# dp formulafor i in range(1, len(coins)):for j in range(amount + 1):if j < coins[i]:dp[i][j] = dp[i-1][j]else:dp[i][j] = min(dp[i-1][j], dp[i][j-coins[i]] + 1)return dp[-1][-1] if dp[-1][-1] != float('inf') else -1
滚动数组
之前做过的几道完全背包,先物品后背包是求组合种类问题,先背包后物品是求排列种类问题。如上所述,本题只要求满足金额的硬币数,不在意满足金额的结果的顺序,所以物品、背包的遍历顺序都可以。
class Solution:def coinChange(self, coins: List[int], amount: int) -> int:# dp[i][j] represents the smallest number to make j using coins [0, i]dp = [-1] * (amount + 1)dp[0] = 0# dp formulafor i in range(len(coins)):for j in range(amount + 1):if j >= coins[i]:if dp[j] >= 0 and dp[j-coins[i]] >= 0:dp[j] = min(dp[j], dp[j-coins[i]] + 1)elif dp[j] == -1 and dp[j-coins[i]] >= 0:dp[j] = dp[j-coins[i]] + 1elif dp[j] >= 0 and dp[j-coins[i]] == -1:dp[j] = dp[j]else:dp[j] = -1return dp[-1]
正确初始化的解法
class Solution:def coinChange(self, coins: List[int], amount: int) -> int:# dp[i][j] represents the smallest number to make j using coins [0, i]dp = [float('inf')] * (amount + 1)dp[0] = 0# dp formulafor i in range(len(coins)):for j in range(amount + 1):if j >= coins[i]:dp[j] = min(dp[j], dp[j-coins[i]] + 1)return dp[-1] if dp[-1] != float('inf') else -1
279. 完全平方数
题目链接 | 理论基础
本题乍一看和完全背包没什么关系。将完全平方数 1,4,9 … 看作是物品,n 看作是背包容量的话,就又是一道标准的完全背包问题:求填满背包使用的最少物品数。抽象过后,本题和上一题几乎是一模一样。
唯一的区别在于,由于 n 的范围很大,在 n 取较大值的时候会耗时较长。二维数组会直接超时,而滚动数组也需要直接利用更新范围来减少遍历时间。这也是第一道二维数组无法解题的背包问题。
class Solution:def numSquares(self, n: int) -> int:# dp[j] represents the number of ways to make jdp = [float('inf')] * (n+1)dp[0] = 0max_sqrt_num = int(sqrt(n))# dp formulafor i in range(max_sqrt_num):for j in range((i+1) * (i+1), n+1):dp[j] = min(dp[j], dp[j-(i+1)*(i+1)] + 1)return dp[-1]
相关文章:
 | 322. 零钱兑换 | 279. 完全平方数)
代码随想录算法训练营Day45 | 70. 爬楼梯 (进阶) | 322. 零钱兑换 | 279. 完全平方数
文章目录 70. 爬楼梯 (进阶)322. 零钱兑换二维数组滚动数组 279. 完全平方数 70. 爬楼梯 (进阶) 题目链接 | 理论基础 以完全背包的思路来解题,正如组合总和 Ⅳ 中提到的一样。在本题中,先背包后物品的思路就显得非常合理明显了。 本题中的物品就是可…...
| 动态规划Part11:最长公共子序列)
算法训练营第四十一天(9.2)| 动态规划Part11:最长公共子序列
Leecode 1143.最长公共子序列 题目地址:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目类型:最长子序列 class Solution { public:int longestCommonSubsequence(string text1, string text2) {int m text1.size(), n t…...

k8s基于rbac权限管理serviceAccount授权管理
测试通过http访问apiServer curl没有证书不能通过https来访问apiServer需要使用kubectl代理 #使用kubectl代理 kubectl proxy --port8111& #curl访问 api/v1 是资源所属群组/版本 即创建资源时定义的apiVersion #后边跟的是要访问的资源 #查看所有命名空间 #查看核心资源用…...

linux URL访问工具
URL访问工具 有时候想在命令行下通过http访问接口/网页,可以使用curl来进行操作 发起请求 curl www.baidu.com 会返回网页内容 参数选项 -i参数 使用-i参数,会返回响应header curl -i www.baidu.com -I参数 使用-I参数,只会返回响应header cu…...

CCF-CSP 29次 第五题【202303-5 施肥】
计算机软件能力认证考试系统 题解(35分): 枚举每个区间,再枚举每个施肥车,看所有的施肥车能不能把这个区间填满 #include<bits/stdc.h> using namespace std; const int N410; int n,m; typedef pair<int,…...
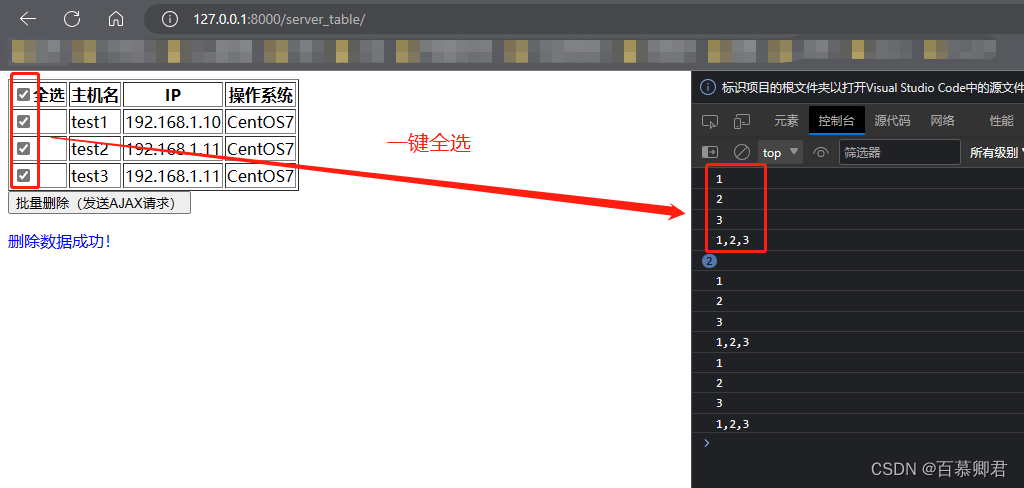
前端基础4——jQuery
文章目录 一、基本了解1.1 导入jQuery库1.2 基本语法1.3 选择器 二、操作HTML2.1 隐藏和显示元素2.2 获取与设置内容2.3 获取、设置和删除属性2.4 添加元素2.5 删除元素2.6 设置CSS样式 三、jQuery Ajax3.1 基本语法3.2 回调函数3.3 常用HTTP方法3.4 案例一3.4.1 准备工作3.4.2…...
测试人:“躺平?不可能的“, 盘点测试人在职场的优势
之前有这么一个段子:有人喜欢创造世界,他们做了程序员;有人喜欢拯救世界,他们做了测试员!近几年,测试工程师在企业究竟是怎么样的发展?随着企业对于用户体验的满意度越来越重视,更加…...

C++:初识类与this指针
文章目录 前言一、类类的定义和实例化类的访问限定符类的作用域计算类的大小 二、类的成员函数的this指针总结 个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》 前言 一、类 类的定义和实例化 注意类定义结束时后面分号( ; )不能省略。 类…...

2023应届生java面试紧张失误之一:CAS口误说成开心锁-笑坏面试官
源于:XX网,如果冒犯,表示歉意 面试官:什么是CAS 我:这个简单,开心锁 面试官:WTF? 我:一脸自信,对,就是这个 面试官:哈哈大笑ÿ…...

Excel_VBA程序文件的加密及解密说明
VBA应用技巧及疑难解答 Excel_VBA程序文件的加密及解密 在您看到这个文档的时候,请和我一起念:“唵嘛呢叭咪吽”“唵嘛呢叭咪吽”“唵嘛呢叭咪吽”,为自己所得而感恩,为付出者赞叹功德。 本不想分享之一技术,但众多学…...

Flutter关于StatefulWidget中State刷新时机的一点实用理解
刚入门flutter开发,使用StatefulWidget踩了很多坑,就我遇到典型问题谈谈见解。 1.initState方法只会在控件初始化的时候执行一遍。 2.控件内部执行setState方法,则会每次执行build方法。 3.控件销毁会执行dispose方法,所以一些…...

CS420 课程笔记 P2 - 内存编辑和基础的 GameHacking 尝试
文章目录 IntroductionOperating SystemToolsMemory ScanningMemory ScanExamples!Conclusion Introduction 本节将介绍操作系统的基础知识和内存扫描,这可以说是 game hacking 中最重要的技能,我们不会深入讨论操作系统,因为这本身就是一门…...

【sql】MongoDB 查询 高级用法
【sql】MongoDB 查询 高级用法 一、基本查询指定字段 db.getCollection(students).find({}, {name: 1, score: 1}) 二、指定字段别名 db.getCollection(students).find({}, {"name":1, "score":1, "grade":"$grade.grade"}) 这里将…...

监督学习的介绍
一、定义 监督学习是利用一组已知类别的样本调整分类器的参数,使其达到所要求性能的过程,也称为监督训练或有教师学习。它是一种机器学习的方法,目的是让模型能够从已知的输入和输出之间的关系中学习,并且能够对新的输入做出正确…...

【DRONECAN】(三)WSL2 及 ubuntu20.04 CAN 驱动安装
【DRONECAN】(三)WSL2 及 ubuntu20.04 CAN 驱动安装 前言 这一篇文章主要介绍一下 WSL2 及 ubuntu20.04 CAN 驱动的安装,首先说一下介绍本文的目的。 大家肯定都接触过 ubuntu 系统,但是我们常用的操作系统都是 Windows&#x…...
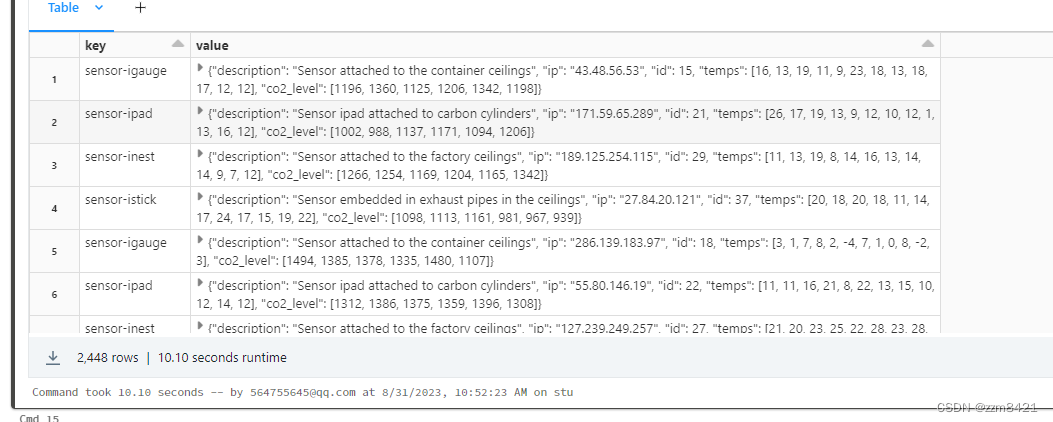
Databricks 入门之sql(二)常用函数
1.类型转换函数 使用CAST函数转换数据类型(可以起别名) SELECTrating,CAST(timeRecorded as timestamp) FROMmovieRatings; 支持的数据类型有: BIGINT、BINARY、BOOLEAN、DATE 、DECIMAL(p,s)、 DOUBLE、 FLOAT、 INT、 INTERVAL interva…...
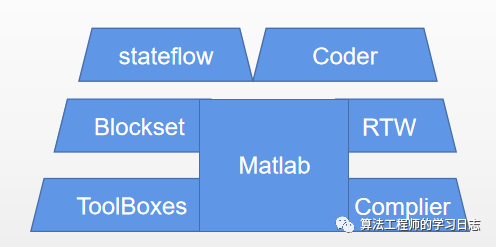
Simulink建模与仿真(3)-Simulink 简介
分享一个系列,关于Simulink建模与仿真,尽量整理成体系 1、Simulink特点 Simulink是一个用来对动态系统进行建模、仿真和分析的软件包。使用Simulink来建模、分析和仿真各种动态系统(包括连续系统、离散系统和混合系统),将是一件非常轻松的事…...

(超简单)将图片转换为ASCII字符图像
将一张图片转换为ASCII字符图像 原图: 效果图: import javax.imageio.ImageIO; import java.awt.image.BufferedImage; import java.io.File; import java.io.FileWriter; import java.io.IOException;public class ImageToASCII {/*** 将图片转换为A…...

In-Context Retrieval-Augmented Language Models
本文是LLM系列文章,针对《In-Context Retrieval-Augmented Language Models》的翻译。 上下文检索增强语言模型 摘要1 引言2 相关工作3 我们的框架4 实验细节5 具有现成检索器的上下文RALM的有效性6 用面向LM的重新排序改进上下文RALM7 用于开放域问答的上下文RALM…...

多种免费天气api
多种免费天气api推荐 一、高德天气二、格点天气三、香港天文台 一、高德天气 api说明文档:https://lbs.amap.com/api/webservice/guide/api/weatherinfo 实例代码: import requests# 香港天文台API的URL api_url "https://restapi.amap.com/v3/w…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
