算法训练营 day51 动态规划 打家劫舍系列
算法训练营 day51 动态规划 打家劫舍系列
打家劫舍
198. 打家劫舍 - 力扣(LeetCode)
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
-
确定dp数组(dp table)以及下标的含义
dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。
-
确定递推公式
决定dp[i]的因素就是第i房间偷还是不偷。
如果偷第i房间,那么dp[i] = dp[i - 2] + nums[i] ,即:第i-1房一定是不考虑的,找出 下标i-2(包括i-2)以内的房屋,最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。
如果不偷第i房间,那么dp[i] = dp[i - 1],即考 虑i-1房,(注意这里是考虑,并不是一定要偷i-1房,这是很多同学容易混淆的点)
然后dp[i]取最大值,即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
-
dp数组如何初始化
从递推公式dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);可以看出,递推公式的基础就是dp[0] 和 dp[1]
从dp[i]的定义上来讲,dp[0] 一定是 nums[0],dp[1]就是nums[0]和nums[1]的最大值即:dp[1] = max(nums[0], nums[1]);
-
定遍历顺序
dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的,那么一定是从前到后遍历!
-
举例推导dp数组
以示例二,输入[2,7,9,3,1]为例。

红框dp[nums.size() - 1]为结果。
public static int rob(int[] nums) {int[] dp = new int[nums.length];if (nums.length<2){return nums[0];}dp[0] = nums[0];dp[1] = Math.max(dp[0],nums[1]);for (int i = 2;i < nums.length; i++) {dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i]);}return dp[nums.length-1];}
打家劫舍II
213. 打家劫舍 II - 力扣(LeetCode)
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
这道题目和198. 打家劫舍 是差不多的,唯一区别就是成环了。
对于一个数组,成环的话主要有如下三种情况:
- 情况一:考虑不包含首尾元素

- 情况二:考虑包含首元素,不包含尾元素

- 情况三:考虑包含尾元素,不包含首元素

注意我这里用的是"考虑",例如情况三,虽然是考虑包含尾元素,但不一定要选尾部元素! 对于情况三,取nums[1] 和 nums[3]就是最大的。
而情况二 和 情况三 都包含了情况一了,所以只考虑情况二和情况三就可以了。
分析到这里,本题其实比较简单了。 剩下的和198. 打家劫舍 就是一样的了。
class Solution {public int rob(int[] nums) {if (nums == null || nums.length == 0) return 0;if (nums.length == 1) return nums[0];return Math.max(robAction(nums,0, nums.length-2),robAction(nums,1, nums.length-1));}public int robAction(int[] nums, int start, int end) {if(start==end) return nums[start];int[] dp = new int[nums.length];dp[start] = nums[start];dp[start+1] = Math.max(nums[start],nums[start+1]);for (int i = start+2; i <=end ; i++) {dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i]);}return dp[end];}
}
打家劫舍III
337. 打家劫舍 III - 力扣(LeetCode)
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
这道题目算是树形dp的入门题目,因为是在树上进行状态转移,我们在讲解二叉树的时候说过递归三部曲,那么下面我以递归三部曲为框架,其中融合动规五部曲的内容来进行讲解。
-
确定递归函数的参数和返回值
这里我们要求一个节点 偷与不偷的两个状态所得到的金钱,那么返回值就是一个长度为2的数组。
dp数组(dp table)以及下标的含义:下标为0记录不偷该节点所得到的的最大金钱,下标为1记录偷该节点所得到的的最大金钱。
所以本题dp数组就是一个长度为2的数组!
-
确定终止条件
在遍历的过程中,如果遇到空节点的话,很明显,无论偷还是不偷都是0,所以就返回
-
确定遍历顺序
首先明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。
通过递归左节点,得到左节点偷与不偷的金钱。
通过递归右节点,得到右节点偷与不偷的金钱。
-
确定单层递归的逻辑
如果是偷当前节点,那么左右孩子就不能偷,val1 = cur.val + left[0] + right[0]; (如果对下标含义不理解就再回顾一下dp数组的含义)
如果不偷当前节点,那么左右孩子就可以偷,至于到底偷不偷一定是选一个最大的,所以:val2 = max(left[0], left[1]) + max(right[0], right[1]);
最后当前节点的状态就是{val2, val1}; 即:{不偷当前节点得到的最大金钱,偷当前节点得到的最大金钱}
-
举例推导dp数组
以示例1为例,dp数组状态如下:(注意用后序遍历的方式推导)

最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱。
class Solution {public int rob(TreeNode root) {int[] res = robTree(root);return Math.max(res[0],res[1]);}public int[] robTree(TreeNode root) {int[] res = new int[2];if (root==null) return new int[]{0,0};int[] left = robTree(root.left);int[] right = robTree(root.right);res[0] = Math.max(left[0],left[1])+Math.max(right[0],right[1]);res[1] = root.val +left[0]+right[0];return res;}
}
相关文章:

算法训练营 day51 动态规划 打家劫舍系列
算法训练营 day51 动态规划 打家劫舍系列 打家劫舍 198. 打家劫舍 - 力扣(LeetCode) 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统&#…...

【蓝桥集训】第六天——递归
作者:指针不指南吗 专栏:Acwing 蓝桥集训每日一题 🐾或许会很慢,但是不可以停下来🐾 文章目录1.树的遍历2.递归求阶乘3.求斐波那契数列1.树的遍历 一个二叉树,树中每个节点的权值互不相同。 现在给出它的后…...
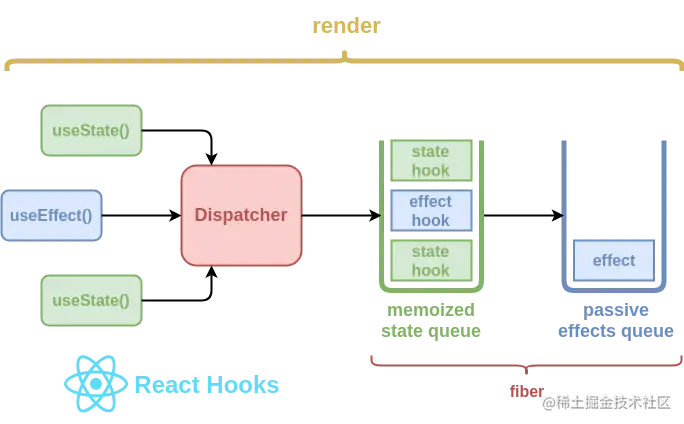
react源码中的hooks
今天,让我们一起深入探究 React Hook 的实现方法,以便更好的理解它。但是,它的各种神奇特性的不足是,一旦出现问题,调试非常困难,这是由于它的背后是由复杂的堆栈追踪(stack trace)支…...

038.Solidity入门——25调用其他合约的方法
Solidity 提供了几种方式用于调用其他合约:方法描述直接调用使用 address.call 函数,可以向另一个合约发送消息并返回结果。低级调用使用 address.call 或 address.callcode 函数,可以执行一个外部合约中的代码。与直接调用不同,低…...
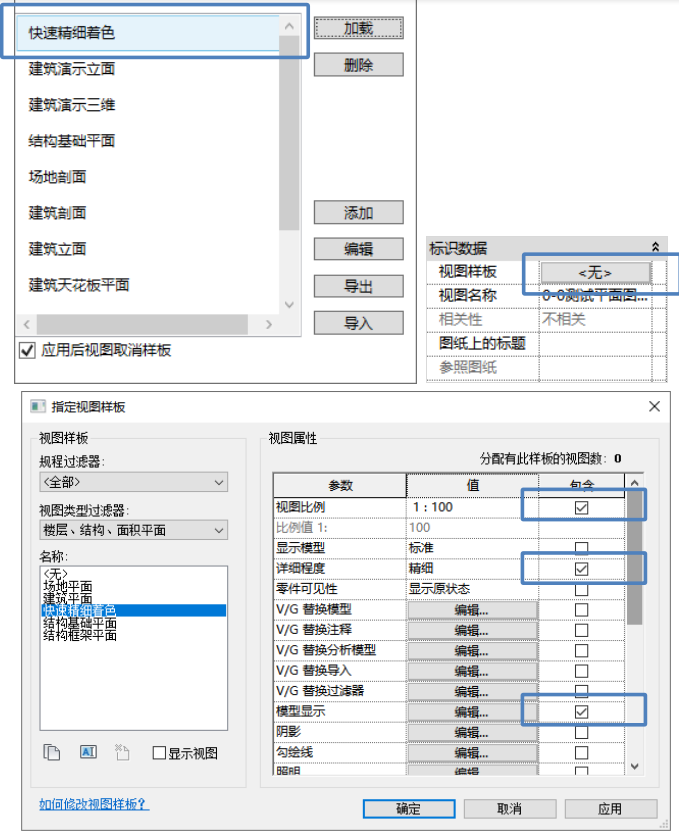
Revit项目浏览器的标准设置应用和快速视图样板?
一、Revit项目浏览器的标准设置应用 设计院阶段的BIM应用,主要是Revit出施工图方面,需要涉及到很多标准的制定方面的问题,而且这个标准不仅仅是一个命名标准,还有很多的符合本院的出图标准等等,本期就不做详细讨论&…...

安装MQTT Server遇到报错“cannot verify mosquitto.org‘s certificate”,该如何解决?
MQTT是基于发布/订阅的轻量级即时通讯协议,很适合用于低带宽、不稳定的网络中进行远程传感器和控制设备通讯等操作中。在我们的软件研发中,也经常使用MQTT协议进行消息通信等。今天来和大家分享一些关于在安装MQTT Server中遇到的疑难问题及解决思路。当…...

程序员如何向架构师转型?看完就明白该怎么做了
软件行业技术开发从业人员众多,但具备若干年开发经验的普通的开发人员往往面临个人发展的瓶颈,即如何从普通开发人员转型成高层次的系统架构师和技术管理人员。想成为一名架构师,应当具备全面的知识体系,需要进行系统的学习和实践…...
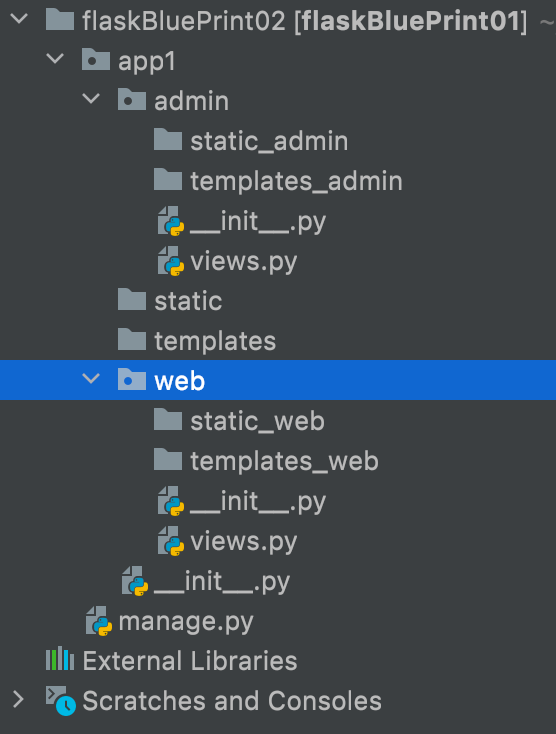
Flask入门(9):蓝图
目录9.蓝图9.1 概述9.2 蓝图项目结构结构1结构29.3 添加前缀9.4 静态文件9.5 模板9.6 构建 URLs9.蓝图 参考:http://www.pythondoc.com/flask/blueprints.html 9.1 概述 Flask 使用了 蓝图 的概念在一个应用或者跨应用中构建应用组件以及支持通用模式。 蓝图很好…...

跑步戴哪种耳机好,最适合运动跑步的蓝牙耳机
经常跑步使用的耳机,还是要选择佩戴着舒适以及牢固的运动耳机最为合适,在运动当中会遇到耳机掉落或者长时间佩戴耳道感到难受的现象发生,那么什么蓝牙耳机是最适合运动当中佩戴呢?下面这些耳机分享希望能够帮助大家。 1、南卡Run…...

微信小程序实现瀑布流布局
微信小程序实现瀑布流布局1、简单实例,纯图片后台返回图片高度https://blog.csdn.net/qq_45967222/article/details/1190318762、纯图片后台返回图片高度、通过wx.getImageInfo获取在线图片高度、按照奇数偶数来显示https://blog.csdn.net/baidu_35290582/article/d…...

2023最新网络工程师HCIA-Datacom“1000”道题库,光速刷题拿证
HCIA认证是华为认证体系的初级认证,可以说是网工进入IT行业的一张从业资格证! HCIA-Datacom考试覆盖数通基础知识 包括 TCP/IP 协议栈基础知识,OSPF 路由协议基本原理以及在华为路由器中的配置实现,以太网技术、生成树、VLAN 原…...

[蓝桥杯] 递归与递推习题训练
文章目录 一、递归实现指数型枚举 1、1 题目描述 1、2 题解关键思路与解答 二、递归实现排列型枚举 2、1 题目描述 2、2 题解关键思路与解答 三、递归实现组合型枚举 3、1 题目描述 3、2 题解关键思路与解答 四、带分数 4、1 题目描述 4、2 题解关键思路与解答 五、费解的开关…...

领航智能汽车信息安全新征程 | 云驰未来乔迁新址
2月20日,在北京朝阳百子湾东朝时代创意园,云驰未来迎来乔迁之喜,智能汽车和自动驾驶领域的行业领导、合作伙伴与客户、投资人及媒体嘉宾齐聚现场,共同见证云驰未来迈上新的发展征程。 作为中国智能网联汽车和自动驾驶信息安全行业…...
Kaldi语音识别技术(七) ----- 训练GMM
Kaldi语音识别技术(七) ----- GMM 文章目录Kaldi语音识别技术(七) ----- GMM训练GMMtrain_mono.sh 用于训练GMM训练GMM—生成文件训练GMM—final模型查看训练GMM—final.occs查看训练GMM—对齐信息查看训练GMM—fsts.*.gz查看训练GMM—tree决策树查看align_si.sh 用于对齐训练G…...

Java 集合基础
文章目录一、集合概念二、ArrayList1. 构造方法和添加方法2. 常用方法三、案例演示1. 存储字符串并遍历2. 存储学生对象并遍历3. 键盘录入学生对象并遍历一、集合概念 编程的时候如果要存储多个数据,使用长度固定的数组存储格式,不一定满足我们的需要&a…...

Day896.MySql的kill命令 -MySQL实战
MySql的kill命令 Hi,我是阿昌,今天学习记录的是关于MySql的kill命令的内容。 在 MySQL 中有两个 kill 命令: 一个是 kill query 线程 id,表示终止这个线程中正在执行的语句;一个是 kill connection 线程 id&#…...

L2-010 排座位
布置宴席最微妙的事情,就是给前来参宴的各位宾客安排座位。无论如何,总不能把两个死对头排到同一张宴会桌旁!这个艰巨任务现在就交给你,对任何一对客人,请编写程序告诉主人他们是否能被安排同席。 输入格式࿱…...
C++的完美讲解,还不快来看看?
目录 简介: 创建C程序: Windows编译简介: Hello,C World! 简介: C融合了3中不同的编程传统:C语言代表的过程性传统、C在C语言基础上添加的类代表的面向对象语言的传统以及C模板支持的通用编程传统。一般来说,计算机语言…...
C语言学习_DAY_5_循环结构while和for语句【C语言学习笔记】
高质量博主,点个关注不迷路🌸🌸🌸! 目录 I. 案例引入 II. while语句 III. do while语句 IV. for语句 前言: 书接上回,判断结构已经解决,接下来是另一种很重要的结构:循环结构的实…...

JavaScript高级程序设计读书分享之4章——4.3垃圾回收
JavaScript高级程序设计(第4版)读书分享笔记记录 适用于刚入门前端的同志 4.3.3 性能 垃圾回收程序会周期性运行,如果内存中分配了很多变量,则可能造成性能损失,因此垃圾回收的 时间调度很重要。尤其是在内存有限的移动设备上,垃圾…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...
