算法基础第三章
算法基础第三章
- 1、dfs(深度搜索)
- 1.1、 递归+回溯
- 1.2、递归+剪枝(剪枝就是判断接下来的递归都不会满足条件,直接回溯,不再继续往下无意义的递归)
- 2、bfs(广度搜索)
- 2.1、最优路径(只适合于边权都相等的题)
- 3、邻接表存储树和图(邻接表就是单链表 )
- 3.1、深度优先遍历(特殊的深搜)
- 3.2、宽度优先遍历(特殊的宽搜)
- 3.3、有向图的拓扑序列(有环的有向图不可能是拓扑序列)
- 4、最短路
- 4.1、单源最短路
- 4.1.1、所有边权都是整数
- 4.1.2、存在负权边
- 4.2、多源汇最短路
- 5、最小生成树
- 5.1、prim算法
- 5.2、Kruskal算法(稀疏图)
- 6、二分图
- 6.1、染色法
- 6.2、匈牙利算法
1、dfs(深度搜索)
1.1、 递归+回溯
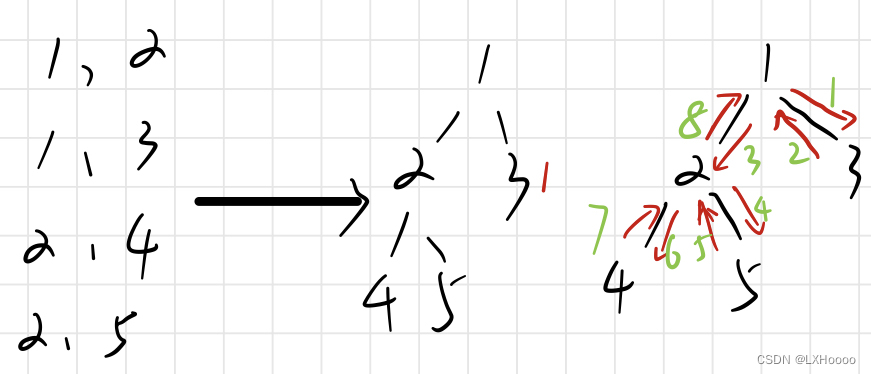
- 解析:下图为1,2,3三个数的全排列过程,从0层开始,一直往下递归,直到数的个数用完,每次使用了一个数需要将这个数标记为已使用过,回溯的时候再恢复为未使用过。
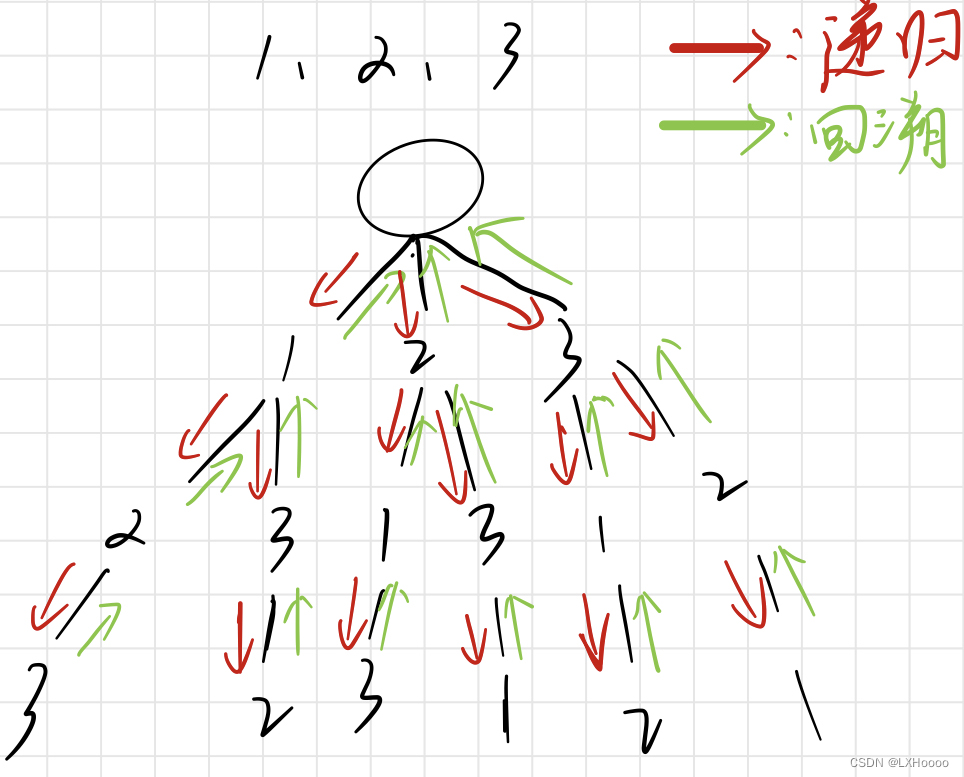
- 题目链接:一个数的全排列
- 代码
#include <iostream>
#include<stdio.h>//加了这个头文件时间快了1msusing namespace std;const int N = 7;
bool use[N];//这个数被用过的话则记为true,排列的时候位置上只能放没被用过的
int path[N],n;
void dfs(int num)
{if(num == n)//输入3,怎有3个空位排列,填满之后就输出{for(int i = 0; i < n; i++){printf("%d ",path[i]);}puts("");return;}for(int i = 1; i <= n; i++){if(!use[i]){path[num] = i;use[i] = true;dfs(num + 1);use[i] = false;}}
}int main() {cin >> n;dfs(0);//从0开始return 0;
}
1.2、递归+剪枝(剪枝就是判断接下来的递归都不会满足条件,直接回溯,不再继续往下无意义的递归)
- 解析:
- 题目链接:n皇后问题
- 代码:代码并没有全a,路过的大佬可以给个补充
#include <iostream>
using namespace std;const int N = 20;
int n;
bool col[N],dg[N],udg[N];
long long ret;void dfs(int num)
{if(num == n){ret++;return;}for(int i = 0; i < n; i++){if(!col[i] && !dg[i+num] && !udg[n-num+i]){col[i] = dg[i+num] = udg[n-num+i] = true;dfs(num+1);col[i] = dg[i+num] = udg[i-num+n] = false;}}
}
int main() {scanf("%d",&n);dfs(0);printf("%lld",ret);
}
2、bfs(广度搜索)
//基本框架,伪代码
queue_init;
while(!queue.empty())
{t = queue.pop();//弹出队头元素queue.push(t.child->node);//这里包括左右子节点
}
2.1、最优路径(只适合于边权都相等的题)
- 解析:
- 题目链接:走迷宫
- 代码
#include <iostream>
#include <algorithm>
#include <cstring>using namespace std;typedef pair<int,int> PII;const int N = 1010;
char g[N][N];//存储地图数据
int d[N][N];//存储距离
int n,m,posx1,posy1,posx2,posy2;//传入的行和列数以及起始终止点的位置
PII q[N*N];//数组模拟队列,需要开元素的个数的大小int bfs(int posx2,int posy2)
{int hh=0,tt=0;//队头和队尾指针q[0] = {posx1-1,posy1-1};//队列初始化,放入起始位置的坐标memset(d,-1,sizeof d);//d初始化为-1,-1表示这个位置还未经过,sizeof(d) = N*N*4,int是个字节,所以乘4d[posx1-1][posy1-1] = 0;//起始位置与自己的距离是0int dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1};//四个方向的移动x和y的坐标的变化while(hh <= tt)//队列非空{auto t = q[hh++];//弹出队头元素for(int i = 0; i < 4; i++)//四个方向的移动{int x = t.first + dx[i],y = t.second + dy[i];if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == '.' && d[x][y] == -1)//这个点未走过且在边界内且无障碍物{d[x][y] = d[t.first][t.second] + 1;//这个点与起始位置的点的距离在上一个点的距离上加1q[++tt] = {x,y};//从队尾压入新的位置的坐标}if(d[posx2-1][posy2-1] != -1)//表示到达终止点,返回{return d[posx2-1][posy2-1];}}}return -1;
}
int main()
{scanf("%d%d%d%d%d%d",&n,&m,&posx1,&posy1,&posx2,&posy2);getchar();for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){scanf("%c",&g[i][j]);}getchar();//读取换行符}printf("%d",bfs(posx2,posy2));return 0;
}
3、邻接表存储树和图(邻接表就是单链表 )
- 树是特殊的有向图,是无环连通图
- 无向图也是一种特殊的有向图,是双向的
- 邻接表的存储代码
#include<cstring>
#include<iostream>
#include<algorithm>using namespace std;const int N = 100010,M = N*2;
int h[N],e[M],ne[M],idx;/* a:被插入的节点* b:新插入的节点,之后有a指向b的边*/
void add(int a,int b)
{e[idx] = b, ne[idx] = h[a],h[a] = idx++;
}
int main()
{memset(h,-1,sizeof h);//h数组是图里面的节点,初始都是指向-1,也就是相当于nullptr
}
3.1、深度优先遍历(特殊的深搜)
- 解析:有向图的遍历,深度遍历,逮住一个起点一直往下递归,每个点只遍历一次,直到结束再回溯再递归,一直遍历完所有的点
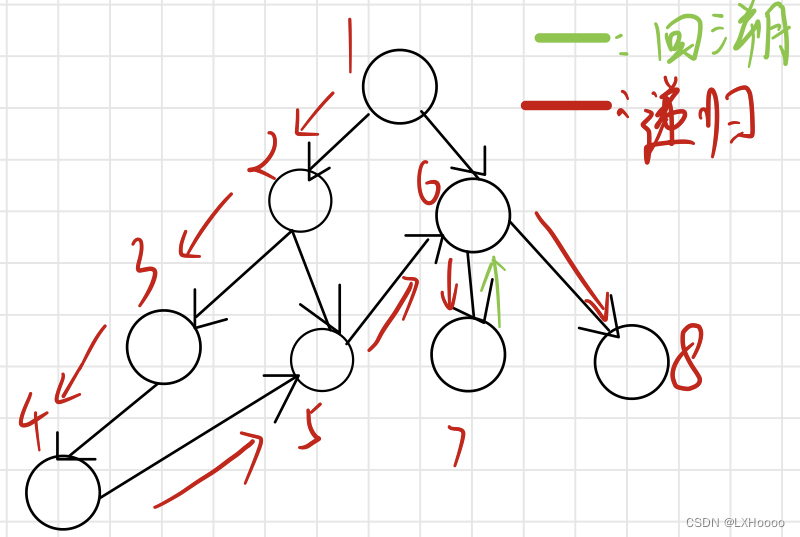
- 题目链接:未找到对应的题目,贴上acwing原题
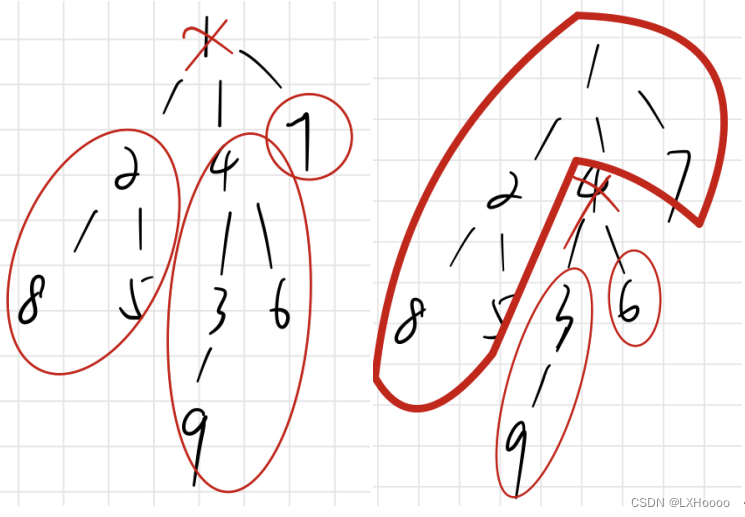
- 题目解析:图中的无向图,可以看到左图删除节点1,有三个连通域,大小分别是3,4,1,最大值为4,我们只需要遍历节点1 的子节点就能得到三个大小。右图删除节点4,三个连通域大小分别为5,2,1,上面连通域的大小我们只要求出节点4的子节点数,用总数减去就能得到。那对应的每删除一个节点都有相应的连通域,要求出这些连通域中最大值中的最小值。
- 代码解析:下面的代码初看是有点绕的,图中举了一个较短的例子遍历,可以先把数组的内容全都列出来,假设从1节点开始:1)dfs(1),i=h[1]=2,j=e[2]=3;2)dfs(3),i=h[3]=3,j=e[3]=1,continue;3)i=ne[3]=-1;4)i=ne[2]=0,j=e[0]=2;5)dfs(2),i=h[2]=6,j=e[6]=5;6)dfs(5),i=h[5]=7,j=e[7]=2,continue;7)i=ne[7]=-1;8)i=ne[6]=4,j=e[4]=4;9)dfs(4),i=h[4]=5,j=e[5]=2,continue;10)i=ne[5]=-1;11)i=ne[4]=1,j=e[1]=1,continue;12)i=ne[1]=-1结束。遍历的顺序是1->3->-1再返回1,接着1->2->5->-1再返回2,接着2->4->-1再返回2,2再返回1,1->-1结束遍历。可以看到3的ne保存这到2路径,也就是直接从1到2,中间省去了1。
- 代码(acwing源码)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 100010, M = N * 2;//因为需要建立两份边,所以 M = 2 * N;int n;
int h[N], e[M], ne[M], idx;
int ans = N;
bool st[N];
//添加边的模板,要求熟练的默写,这部分的解释在 链表 专题中
void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
//返回以u为根的子树中节点的个数,包括u节点
int dfs(int u)
{st[u] = true;int size = 0, sum = 0;//size存储的是以u为根的数的一个子儿子的节点数的最大值//sun存储以u为根的树的节点数, 包括ufor (int i = h[u]; i != -1; i = ne[i]){int j = e[i];if (st[j]) continue;int s = dfs(j); //s存储的就是以 j 为根的子树的节点数,包括 jsize = max(size, s); //每次找出最大的子图的节点数sum += s; //以j为根的树的节点数}size = max(size, n - sum - 1); //求 dfs 遍历的所有子树中最大的节点数的个数和 dfs 未遍历的那棵树的节点数的最大值ans = min(ans, size);return sum + 1; //这里返回的个数加上根节点
}int main()
{scanf("%d", &n);memset(h, -1, sizeof h);for (int i = 0; i < n - 1; i ++ ){int a, b;scanf("%d%d", &a, &b);add(a, b), add(b, a); //处理无向图的添边方式}dfs(1); //可以选择任意一个点开始进行 dfs,又u <= n,且 n 的最小值为1,所以只能从 1 开始//当然本题数据是从 5 开始的,所以对于本题写 dfs (1 ~ 5)均可ACprintf("%d\n", ans);return 0;
}3.2、宽度优先遍历(特殊的宽搜)
- 解析:套用宽度优先搜索的模板,逮住一个点开始,遍历所有的节点,看保存的节点个数是否和输入的相等,相等的话则是全连通的,否则不是
- 题目链接:宽度优先遍历
- 代码
#include <iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N = 1010,M = N * 2;//因为无向图需要建立两份边,所以 M = 2 * N;
int e[M],ne[M],h[N];
int n,m,idx;int bfs()//广度优先遍历
{int hh=0,tt=0;//队头和队尾指针int q[N];//数组模拟队列bool st[N];//是否遍历过标记q[0] = 1;//队列初始化,模板步骤st[1] = true;//这个元素被遍历过了int ret = 0;//保存节点数while(hh <= tt)//队列不为空{int t = q[hh++];//弹出队头for(int i = h[t]; i != -1; i = ne[i])//按照边去遍历{int j = e[i];if(st[j])continue;elsest[j] = true,ret++,q[++tt] = j;//该节点未被遍历过,则压进队尾,标记被遍历,节点数加1}}return ret+1;//因为开始的节点本身没被算进去,需要加1
}
void add(int x,int y)//无向图的建立,前面已经解释过了
{e[idx] = y,ne[idx] = h[x],h[x] = idx++;
}int main() {memset(h,-1,sizeof h);while(cin >> n >> m){if(!n && !m)break;while(m--){int x,y;cin >> x >> y;add(x,y),add(y,x);//建立双边}if(bfs()==n){cout << "YES" << endl;memset(h,-1,sizeof h);//因为输入是有很多图的,处理完一个无序图需要重新清空准备处理下一个无序图memset(e,0,sizeof e);memset(ne,0,sizeof ne);idx = 0;}else{cout << "NO" << endl;memset(h,-1,sizeof h);memset(e,0,sizeof e);memset(ne,0,sizeof ne);idx = 0;}}
}
3.3、有向图的拓扑序列(有环的有向图不可能是拓扑序列)
- 入度:一个点有多少指向自己的边
- 出度:一个点有多少边从自己这出去
- 解析:当一个图按拓扑序排好之后,起点一定是在终点的前面,如图中所示,当按1,2,3排序就是一个拓扑序列,所有边的起点都在终点的前面。当求解一个有向图是否能够组成拓扑排序的时候,也就是看看能否将所有的节点的入度都处理为0,能的话就能拓扑排序,否则就不能

- 题目连接:拓扑排序
- 代码
#include <iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N = 200010;int e[N],ne[N],h[N];
int d[N];
int n,m,idx;
int q[N];//宽搜的模板队列void add(int x,int y)//图的构建
{e[idx] = y,ne[idx] = h[x],h[x] = idx++;
}bool tuposort()//拓扑排序
{int hh = 0,tt = -1;for(int i =1; i <= n; i++){if(!d[i])q[++tt] = i;//首先把所有入度为0的点压入队列}while(hh <= tt)//宽搜模板{int t = q[hh++];//弹出队头,元素还在数组里面,只是用了头尾指针来表示弹出与压入for(int i = h[t]; i != -1; i = ne[i])//宽搜遍历,这个是有向图,不会重复遍历{int j = e[i];d[j]--;//该节点的入度减1if(d[j] == 0)q[++tt] = j;//该节点入度变为0之后就压入队列}}return tt == n-1;//所有的点都能够被入队说明是一个有向无环图,即能构成拓扑排序
}int main() {memset(h,-1,sizeof h);scanf("%d%d",&n,&m);while(m--){int x,y;cin >> x >> y;add(x,y);d[y]++;//保存这个点的入度}if(tuposort()){for(int i = 0; i < n; i++){if(i!=n-1)printf("%d ",q[i]);else printf("%d",q[i]);//答案最后有一个数不能有空格,有空格提交不成功}}else {printf("%d",-1);//无拓扑排序输出-1}
}
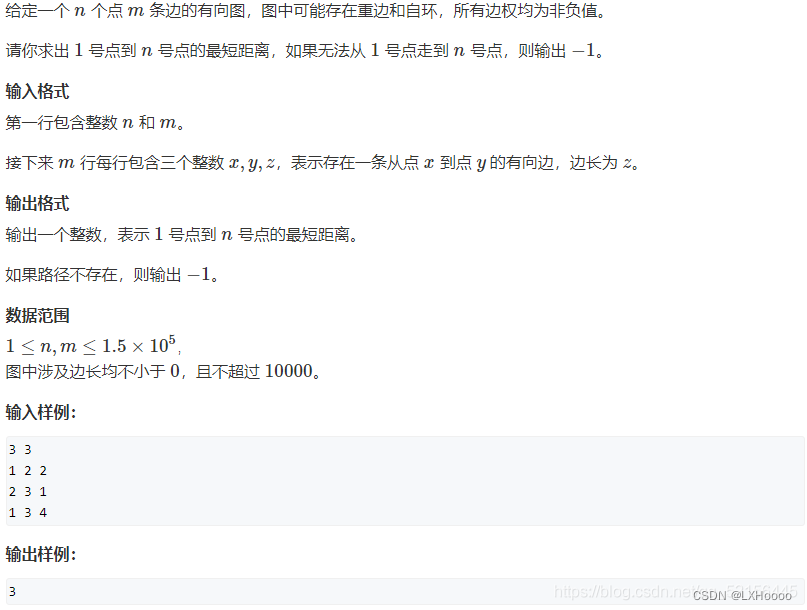
4、最短路
4.1、单源最短路
- 求一个点到其他所有点的最短路
4.1.1、所有边权都是整数
- 朴素Dijkstra:稠密图(邻接矩阵),m(边数)~n^2(点数)
- 模板:
- 1.dist[1] = 0,dist[i] = 正无穷
- 2.for i 1~n(迭代)
- t<-不在s中的,距离最近的点
- s<-t;//s是当前已确定最短距离的点
- 用t更新其他点的距离
- 题目链接:Dijkstra求最短路径
- 代码
- 模板:
class Solution {
public:int networkDelayTime(vector<vector<int>> ×, int n, int k) {const int inf = INT_MAX/2;//构建邻接矩阵int g[n][n];memset(g,0x3f3f3f3f,sizeof g);//这里初始化后的值不等于inffor(auto &t:times){int x = t[0]-1,y = t[1]-1;g[x][y] = min(g[x][y],t[2]);}
-
- //存储距离的数组,初始化为g数组一样的最大值vector<int>dist(n,0x3f3f3f3f);//保存距离dist[k-1] = 0;//k是出发点,将出发点的距离设为0,数组中的坐标与节点值是-1的关系vector<int> st(n,0);//保存是否遍历过的标记for(int i = 0; i < n;i++)//这个循环是遍历n个节点{int t = -1;for(int j = 0; j < n; j++)//这个循环是找到出发点{if(!st[j] && (t == -1 || dist[j] < dist[t])){t = j;}}st[t] = true;//标记这个点被遍历了for(int j = 0; j < n; j++)//这个循环是计算出出发点最到他点的最短距离{dist[j] = min(dist[j],dist[t] + g[t][j]);}}int ans = *max_element(dist.begin(),dist.end());return ans == 0x3f3f3f3f ? -1 : ans;}
};
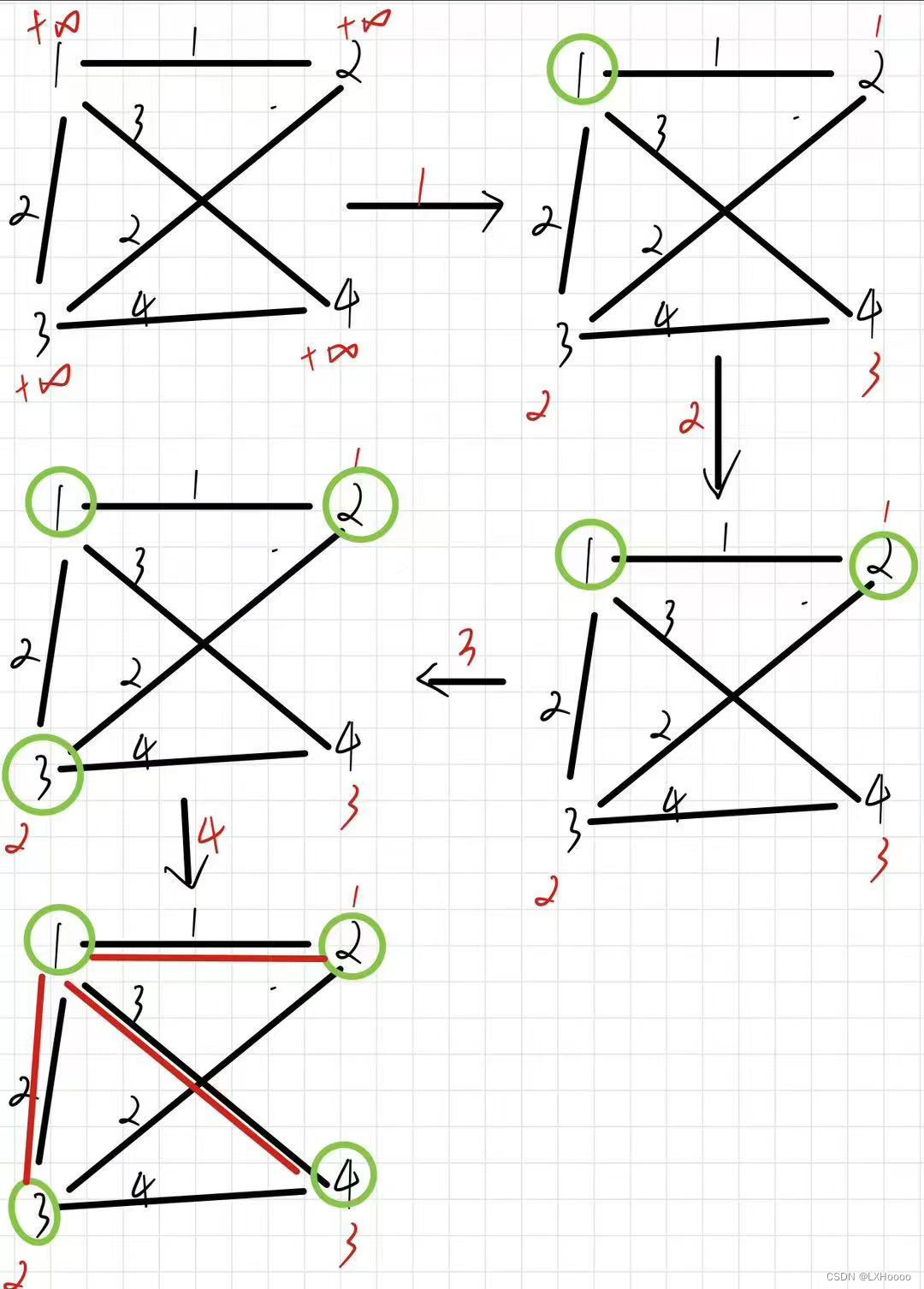
- 堆优化版的Dijkstra算法:稀疏图(邻接表),m(边数)~n(点数)
- 解析:堆优化版的改进是在朴素版的基础上,在for循环找到目标最近点用堆来替代,从而减小时间复杂度,题意中可以看到n和m的数量级是相等的,因此是稀疏图,用邻接表来做
- 题目链接:未找到,acwing原题
- 代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include<vector>
#include<queue>using namespace std;typedef pair<int,int>PII;const int N = 1e6+10;int n,m;
int h[N],w[N],e[N],ne[N],idx;
int dist[N];
bool st[N];void add(int a,int b,int c)
{e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
}int dijkstra()
{memset(dist,0x3f,sizeof dist);dist[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;//优先队列定义一个小根堆heap.push({0,1});//整个代码就是邻接表加宽搜模板,初始化队列while(heap.size()){auto t = heap.top();//取出队头heap.pop();//弹出队头int ver = t.second,distance = t.first;if(st[ver])continue;//是否已经遍历过for(int i = h[ver]; i != -1; i = ne[i])//最短路径替换{int j = e[i];if(dist[j] > dist[ver] + w[i]){dist[j] = dist[ver] + w[i];heap.push({dist[j],j});}}}if(dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}int main()
{scanf("%d%d",&n,&m);memset(h,-1,sizeof h);while(m--){int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c);//添加有向边}printf("%d\n",dijkstra());return 0;
}
4.1.2、存在负权边
- Bellman-Ford算法
- 模板
- for n 次
- for 所有边a,b,w
- dist[b] = min(dist[b],dist[a]+w)
- for 所有边a,b,w
- for n 次
- 题目链接:bellman-ford模板算法
- 代码
- 模板
class Solution {
public:int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {int m = flights.size();//写成int m = flights.size()+10; int dist[m],backup[m];会报错int dist[m+10],backup[m+10];//为了防止超出数组界限,所以在长度上加10memset(dist,0x3f,sizeof dist);dist[src] = 0;//从哪个点开始,那个点起始的距离为0for(int i = 0; i < k+1; i++)//这里k是中转站点,而不是边数,所以是k+1,因为得加上起点{memcpy(backup,dist,sizeof dist);//加备份,防止出现串联for(int j = 0; j < m; j++){auto t = flights[j];dist[t[1]] = min(dist[t[1]],backup[t[0]] + t[2]);//防止串联,因为要满足k的限制,所以必须保证不能用这次的更新去更新后面的距离}}if(dist[dst] > 0x3f3f3f3f/2) return -1;else return dist[dst];}
};
- SPFA算法
- 使用宽搜的队列对Dellman-Ford算法的改进
- 使用SPFA判断负环,也能用于Dijkstra算法解决的最短路径问题
- 题目链接:判断负环
#include <iostream>
#include <queue>
#include <cstring>using namespace std;const int N = 210,M = 2010;
int n,m,a,b,c;
int h[N],e[M],ne[M],w[M],idx;
int dist[N],cnt[N];
bool st[N];//使用邻接表构建图
void add(int a,int b,int c)
{e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
}bool spfa()
{queue<int>q;memset(dist,0x3f,sizeof dist);dist[1] = 0;//因为能到达的话是输出从1号点到n号点的距离,所以1号点的距离初始化为0for(int i = 1; i <= n; i++){st[i] = true;q.push(i);//先把所有的点入队列}while(q.size()){int t = q.front();q.pop();st[t] = false;for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];if(dist[j] > dist[t] + w[i])//这个条件保证了是负边环{dist[j] = dist[t] + w[i];cnt[j] = cnt[t] + 1;if(cnt[j] >= n) return true;//cnt里面存的是边数,如果边数大等于n,那么点数大等于n+1,因为只有n个点,所以一定是有环的if(!st[j]){q.push(j);st[j] = true;}}}}return false;
}int main() {scanf("%d%d",&n,&m);memset(h,-1,sizeof h);while(m--){int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c);}if(spfa())puts("circle");else{if(dist[n] == 0x3f3f3f3f) puts("can't arrive!");elsecout << dist[n];}
}
4.2、多源汇最短路
- 源:起点;汇:终点
- 任选两个点,求这两个点之间的最短路
- Floyd算法
- 模板,用邻接矩阵存储边
- d[i,j]
- for(k=1;k<=n;k++)
- for(i=1; i<=m; i++)
- for(j=1; j<=n; j++)
- d[i,j] = min(d[i,j],d[i,j] + d[k,j]);//使用了动态规划的原理
- for(j=1; j<=n; j++)
- for(i=1; i<=m; i++)
- for(k=1;k<=n;k++)
- d[i,j]
- 题目链接:Floyd算法
- 代码
- 模板,用邻接矩阵存储边
在这里插入代码片
5、最小生成树
5.1、prim算法
-
朴素版:稠密图
- 模板
- dist[i]<-inf
- for(i=0;i<n;i++)
- t<-找到集合外距离最近的点
- 用t更新其他点到集合的距离
- st[t] = true;
- 模板
-
解析:起始每个点存储的距离初始化都是inf,随后随便找到一个点开始,图中从1开始,用1到其他点的距离去更新各个点存储的距离,然后1被放入集合
-
堆优化版(一般不用)
5.2、Kruskal算法(稀疏图)
6、二分图
6.1、染色法
6.2、匈牙利算法
相关文章:

算法基础第三章
算法基础第三章 1、dfs(深度搜索)1.1、 递归回溯1.2、递归剪枝(剪枝就是判断接下来的递归都不会满足条件,直接回溯,不再继续往下无意义的递归) 2、bfs(广度搜索)2.1、最优路径(只适合于边权都相等的题) 3、…...

ElementUI浅尝辄止20:Pagination 分页
分页组件常见于管理系统的列表查询页面,数据量巨大时需要分页的操作。 当数据量过多时,使用分页分解数据。 1.如何使用? /*设置layout,表示需要显示的内容,用逗号分隔,布局元素会依次显示。prev表示上一页…...

Docker从认识到实践再到底层原理(二-1)|容器技术发展史+虚拟化容器概念和简介
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...

什么是大模型?1750亿、700GB的GPT大模型大在哪?
文章目录 什么是大模型?1750亿、700GB的GPT大模型大在哪? 什么是大模型? 在人工智能领域,模型是指一种对数据进行处理和分析的数学结构。模型越复杂,能够处理的数据量和处理的准确性都会得到提高。 随着人工智能技术…...

剑指 Offer 10- II. 青蛙跳台阶问题
剑指 Offer 10- II. 青蛙跳台阶问题 和 剑指 Offer 10- I. 斐波那契数列 很像,改一下初始值就行了。 方法一 class Solution {int mod (int) 1e9 7;public int numWays(int n) {if(n < 1) return 1;int[] dp new int[n 1];dp[1] 1;dp[2] 2;for(int i 3…...

oracle10和11功能说明比较
Oracle 10g/11g的特点和优势 首先,Oracle 10g/11g具有以下几个特点: 1. 可靠性和稳定性:Oracle 10g采用了多种技术来确保数据的可靠性和稳定性,如ACID事务处理和数据备份与恢复机制。它还提供了高可用性的解决方案,如…...
golang-bufio 缓冲写
1. 缓冲写 在阅读这篇博客之前,请先阅读上一篇:golang-bufio 缓冲读 // buffered output// Writer implements buffering for an io.Writer object. // If an error occurs writing to a Writer, no more data will be // accepted and all subsequent…...
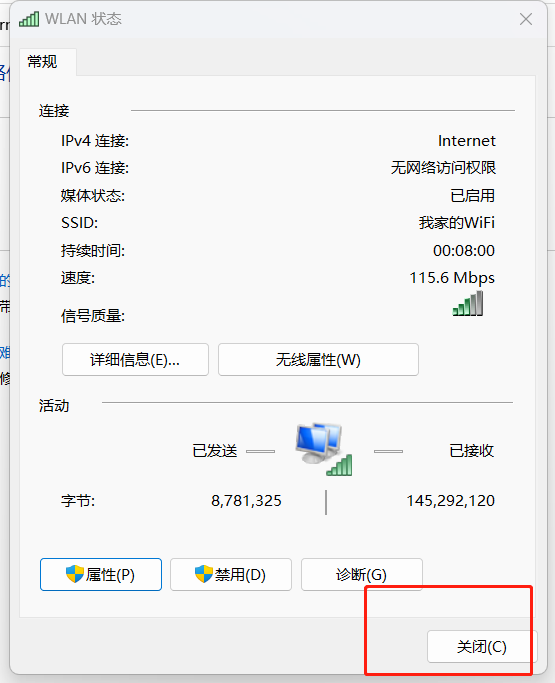
Windows修改电脑DNS
访问浏览器出现无法访问此页面,找不到DNS地址,则可以通过如下方式修改DNS 按下windows键R键(两个键一起按) 出现下面窗口 输入control按回车键(Enter键)就会出现下面的窗口 DNS可以填下面这些: 114.114.114.114 和 114.114.115.115 阿里DNS&a…...

Linux驱动之Linux自带的LED灯驱动
目录 一、简介 二、使能Linux自带LED驱动 三、Linux内核自带LED驱动框架 四、设备树节点编写 五、运行测试 一、简介 前面我们都是自己编写 LED 灯驱动,其实像 LED 灯这样非常基础的设备驱动, Linux 内核已经集成了。 Linux 内核的 LED 灯驱动采用 …...
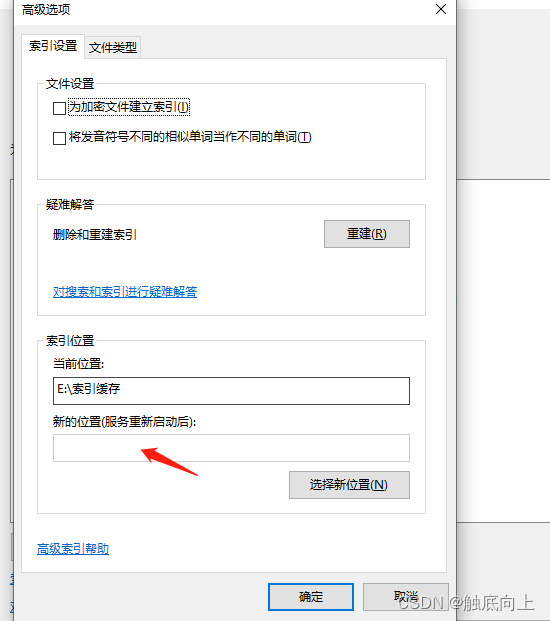
C盘清理 “ProgramData\Microsoft\Search“ 文件夹过大
修改索引存放位置 进入控制面板->查找方式改成大图标, 选择索引选项 进入高级 填写新的索引位置 删除C盘索引信息 删除C:\ProgramData\Microsoft\Search\Data\Applications 下面的文件夹 如果报索引正在使用,参照第一步替换索引位置。关闭索引...

深入了解字符串处理算法与文本操作技巧
深入了解字符串处理算法与文本操作技巧 引言 字符串处理是计算机科学和数据处理的核心领域之一。本博客将深入介绍一些常见的字符串处理算法和文本操作技巧,包括字符串匹配、搜索、正则表达式、字符串操作和文本标准化等。 暴力匹配算法 什么是暴力匹配…...

Python爬虫:打开盈利大门的利器
导言: 随着互联网的迅速发展,越来越多的企业和个人开始意识到数据的重要性。而Python爬虫作为一种自动化获取互联网信息的技术,为人们提供了更便捷、高效的数据获取方式。本文将介绍基于Python爬虫的五种盈利模式,并提供实际案例…...

17.CSS发光按钮悬停特效
效果 源码 <!DOCTYPE html> <html> <head><title>CSS Modern Button</title><link rel="stylesheet" type="text/css" href="style.css"> </head> <body><a href="#" style=&quo…...

CSS中如何实现弹性盒子布局(Flexbox)的换行和排序功能?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 换行(Flexbox Wrapping)⭐ 示例:实现换行⭐ 排序(Flexbox Ordering)⭐ 示例:实现排序⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得…...

spark底层为什么选择使用scala语言开发
Spark 底层使用 Scala 开发有以下几个原因: 基于Scala的语言特性 集成性:Scala 是一种运行在 Java 虚拟机(JVM)上的静态类型编程语言,可以与 Java 代码无缝集成。由于 Spark 涉及到与大量 Java 生态系统的交互&#x…...

基于RabbitMQ的模拟消息队列之三——硬盘数据管理
文章目录 一、数据库管理1.设计数据库2.添加sqlite依赖3.配置application.properties文件4.创建接口MetaMapper5.创建MetaMapper.xml文件6.数据库操作7.封装数据库操作 二、文件管理1.消息持久化2.消息文件格式3.序列化/反序列化4.创建文件管理类MessageFileManager5.垃圾回收 …...

DHorse v1.3.2 发布,基于 k8s 的发布平台
版本说明 新增特性 构建版本、部署应用时的线程池可配置化; 优化特性 构建版本跳过单元测试; 解决问题 解决Vue应用详情页面报错的问题;解决Linux环境下脚本运行失败的问题;解决下载Maven安装文件失败的问题; 升…...
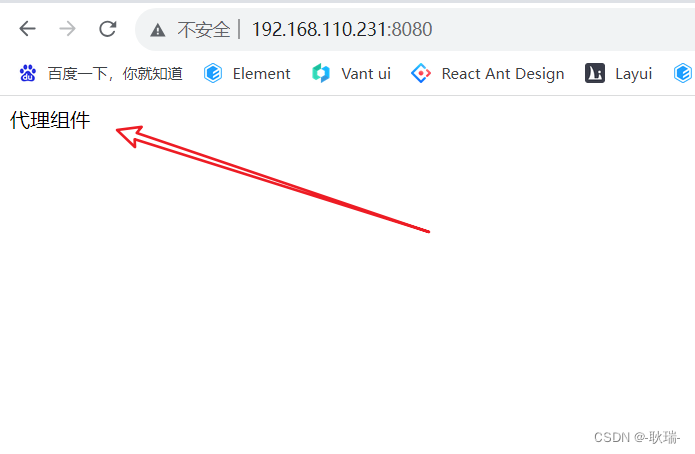
在vue.config.js中配置文件路径代理名
今天在公司项目中看到一个非常有趣的导入路径 crud 先是一蒙 这是个啥 突然想起一个被自己遗漏的知识点 在vue.config.js中配置路径指向 这里 我们随便找一个vue项目 在src下找到 components 目录 如果没有就创建一个 下面找到HelloWorld.vue 如果没有也是自己创建一个就好 然…...

深度学习优化算法相关文章
综述性文章 一个框架看懂优化算法之异同 SGD/AdaGrad/Adam 从 SGD 到 Adam —— 深度学习优化算法概览(一)...

echarts自定义Y轴刻度及其颜色
yAxis: [{min:0,max:5,axisLabel: {color: "#999",textStyle: {fontSize: 14,fontWeight: 400,// 设置分段颜色color: function (value) {console.log("试试", value);if (value 1) {return "rgba(140,198,63,1)";} else if (value 2) {return…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
