0202插入删除-算法第四版红黑树-红黑树-数据结构和算法(Java)
文章目录
- 4 插入
- 4.1 序
- 4.2 向单个2-结点插入新键
- 4.3 向树底部的2-结点插入新键
- 4.4 向一棵双键树(3-结点)中插入新键
- 4.5 颜色调整
- 4.6 根结点总是黑色
- 4.7 向树底部的3-结点插入新键
- 4.8 将红链接在树中向上传递
- 4.9 实现
- 5 删除
- 5.1 删除最小键
- 5.2 删除
- 6 有序性相关方法
- 6.1 floor(),ceiling()
- 6.2 rank()
- 6.3 keys()
- 后记
4 插入
4.1 序
在插入新键时我们可以使用旋转操作帮助我们保证2-3树和红黑树直接的一一对应关系,因为旋转操作可以保持红黑树的两个重要性质:有序性和完美平衡性。下面讲解如何使用旋转操作保持红黑树的另外两个重要性质:不存在两条连续的红色链接和不存在红色的右链接。简单情况热身。
4.2 向单个2-结点插入新键
一棵只含有一个键的红黑树只含有一个2-结点。插入一个新键,如果新键小于老键,我们只需新增一个红色左子结点;如果新键大于老键,那么新增的红色结点形成一条红色的右链接。通过root=rotateLeft(root),将其旋转为红色的左链接,插入操作完成。两种情况的结果均为一棵和单个3-结点等价的红黑树,树的黑链高度1。如下图所示:
4.3 向树底部的2-结点插入新键
用和二叉查找树相同的方式向一棵红黑树中插入一个新键会在树的底部新增一个结点(保证有序性),新插入的结点链接总是红色。如果它的父链接是2-结点,情况同上。
4.4 向一棵双键树(3-结点)中插入新键
这种情况分为3种子情况:新键小于树中的2个键,在两者之间,或者大于两者。每种情况都会产生一个链接到两条红色链接的结点,需要调整:
- 最简单的情况新键大于原树中的两个键,新键被连接到3-结点的右链接。此时树是平衡的,根结点为中间大小的键,它有两条红链接分别和较小和较大的结点相连。此时我们只需要把两条链接颜色有红变黑,得到一棵由3个结点组成、高为2的平衡树。
- 新键小于原树中的两个键,它被链接到最左边的空链接,产出两条连续的红链接。此时将上层的红链接右旋,得到第一种情况。
- 新键介于原树中的两个键之间,它被连接到较小结点的右链接。此时先通过较小结点左旋,形成第二种情况。
图示如下: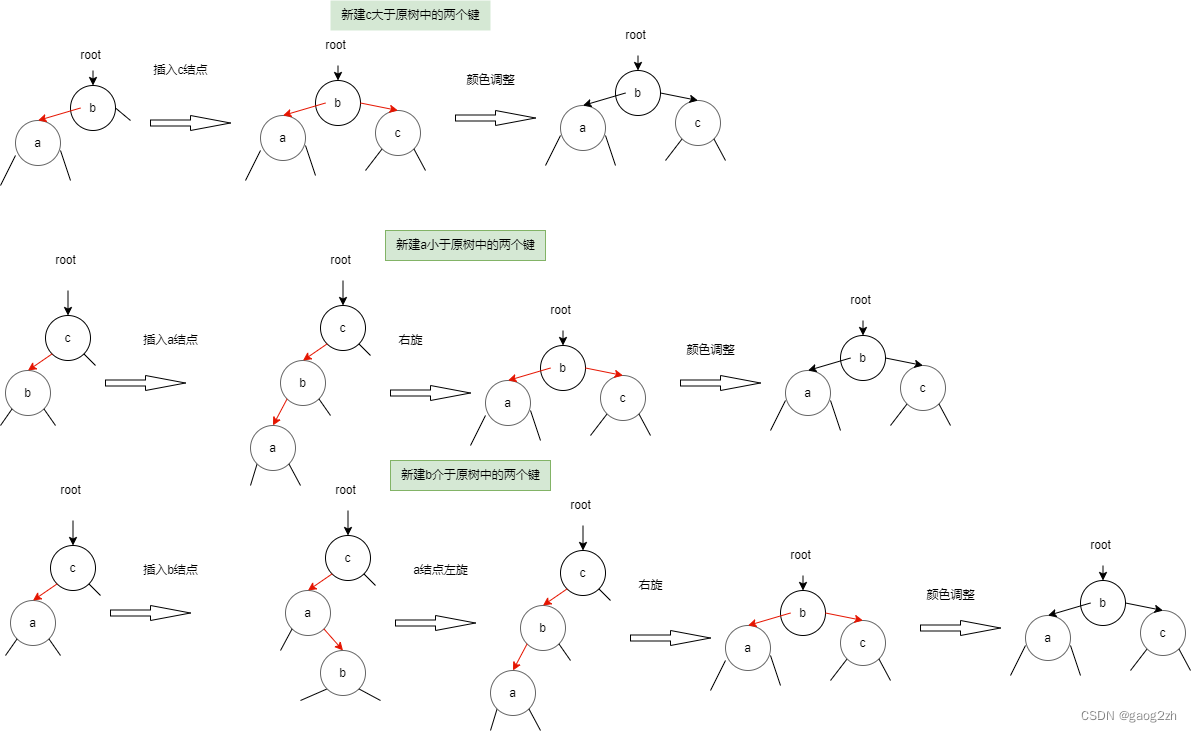
4.5 颜色调整
我们通过flipColor()方法来转换一个结点两个红色子节点的颜色。把两个子节点由红变黑,同时把父结点由黑变红。该操作是局部变换,不会影响整棵树的黑色平衡性。flipColor()源代码如下:
/*** 变化双子链接为红色为黑色,红色转义到父结点* @param p 当前结点*/
private void flipColors(Node p) {p.color = !p.color;p.left.color = !p.left.color;p.right.color = !p.right.color;
}
4.6 根结点总是黑色
上述颜色调整,根结点由黑变红,因此我们每次插入后都需要显示把根结点设为黑色。当根结点有红变黑时,树的黑脸高度+1。
4.7 向树底部的3-结点插入新键
现在假设我们需要在树的底部的一个3-结点下加入一个新结点。前面讨论的3种情况都会出现。颜色转换会使到中结点的链接变红,相当于把它送入父结点。这意味着父结点插入一个新键,继续用相同的办法解决这个问题。
4.8 将红链接在树中向上传递
插入算法的关键步骤:要在一个3-结点下插入新键,先创建一个临时的4-结点,将其分解并将红链接由中间键传递给它的父结点。重复这个过程,知道遇到一个2-结点或者根结点。
4.9 实现
插入给递归实现如下:
/*** 插入键值对* @param key 键* @param value 值*/@Overridepublic void put(K key, V value) {// 树为空if (root == null) {root = new Node(key, value);return;}// 查找key是否在树中,且记录访问路径Stack<Node> stack = new Stack<>();Node cur = root;Node p = null;int type = 0;while (cur != null) {stack.push(cur);p = cur;int cmp = key.compareTo(cur.key);if (cmp < 0) {cur = cur.left;type = 1;} else if (cmp > 0) {cur = cur.right;type = 2;} else {cur.value = value;return;}}// key不在树中Node n = new Node(key, value);if (type == 1) {// 新结点为左子结点p.left = n;} else {// 新结点为右子结点p.right = n;}// 插入新结点后,为满足红黑树性质沿遍历路径自下向上做平衡调整
// boolean ajusted = false;while (!stack.isEmpty()) {
// ajusted = false;cur = stack.pop();cur.n += 1;// 如果右链接为红色且左链接为黑色,则左旋if (isRed(cur.right) && !isRed(cur.left)) {
// ajusted = true;if (cur == root) {root = cur = rotateLeft(cur);} else {p = stack.peek();if (p.left == cur) {p.left = cur = rotateLeft(cur);} else {p.right = cur = rotateLeft(cur);}}}// 如果左链接和左链接的左链接都为红色,则右旋if (isRed(cur.left) && isRed(cur.left.left)) {
// ajusted = true;if (cur == root) {root = cur = rotateRight(cur);} else {p = stack.peek();if (p.left == cur) {p.left = cur = rotateRight(cur);} else {p.right = cur = rotateRight(cur);}}}// 如果左右链接都为红色,则把红色转移到父链接if (isRed(cur.left) && isRed(cur.right)) {
// ajusted = true;flipColors(cur);}
// // 如果当前没做调整,那么它的祖先结点也无需调整
// if (!ajusted) {
// break;
// }}// 剩余祖先结点计数计算
// for (Node node : stack) {
// node.n++;
// }// 保证根结点为黑色root.color = BLACK;}
5 删除
5.1 删除最小键
从树底部的3-结点删除键很简单,但是2-结点删除后,一般会替换为空链接,会破坏树的完美平衡性。所以为了确保不会删除一个2-结点,在沿着左链接向下过程中:
- 如果当前结点的左子结点不是2-结点,完成
- 如果当前结点是2-结点而它的亲兄弟结点不是2-结点,把左子结点的兄弟结点中的一个键移动到左子结点中
- 如果当前结点的左子结点和它的亲兄弟结点都是2-结点,将左子结点、父结点中的最小键和左子结点最近的兄弟结点合并为一个4-结点
在遍历完成后,最后得到一个含有最小键的3-结点或者4-结点,直接删除。然后在回头向上分解所有的4-结点。
非递归代码如下:
/*** 删除最小结点* @return 最小结点对应的value*/public void deleteMin() {if (isEmpty()) {throw new NoSuchElementException("BST underflow");}// 如果根结点左右链接都为黑色,变为4-结点if (!isRed(root.left) && !isRed(root.right)) {root.color = RED;}root = deleteMin(root);if (!isEmpty()) {root.color = BLACK;}
}/*** 删除以p为根结点的树中最小结点* @param p 根结点* @return 删除最小结点后的新树*/
private Node deleteMin(Node p) {// 目标结点的左子树Node pl;// 目标结点的父结点Node pp = null;// 栈记录遍历结点(路径),用于删除后自下向上调整红黑树,以满足红黑树的性质Stack<Node> stack = new Stack<>();while ((pl = p.left) != null) {// 如果左链接为2-结点,从兄弟结点或者父结点借if (!isRed(pl) && !isRed(pl.left)) {p = moveRedLeft(p);if (pp != null) {pp.left = p;}}// 记录遍历结点stack.push(p);// 继续沿左子树遍历pp = p;p = pp.left;}// pp为空说明要删除的为根结点if (pp == null) {return null;} else {// 要删除的结点为非根结点,父结点的左链接置空pp.left = null;}// 调整删除结点后的二叉树,以满足红黑树的性质while (!stack.isEmpty()) {p = stack.pop();p.n--;if (!stack.isEmpty()) {stack.peek().left = balance(p);} else {return balance(p);}}return null;
}
5.2 删除
在查找路径上进行和删除最小键相同的变换,可以保证在查找过程中任意当前结点不是2-结点。如果被查找的键在树的底部,可以直接删除;如果不在,我们需要把它和它的后继结点交换,问题转换为在一棵根结点不是2-结点的子树中删除最小的键。
非递归代码如下:
/*** 删除指定的key* @param key 指定key*/
public void delete(K key) {if (key == null) {throw new IllegalArgumentException("argument to delete() is null");}if (!contains(key)) {return;}// if both children of root are black, set root to redif (!isRed(root.left) && !isRed(root.right)) {root.color = RED;}root = delete(root, key);if (!isEmpty()) {root.color = BLACK;}
}/*** 在以h为根结点的树中删除指定key* @param h 树的根结点* @param key key* @return 删除后调整完的新树*/private Node delete(Node h, K key) {// assert get(h, key) != null;// 存储遍历的结点Stack<Node> stack = new Stack<>();Node t;Node pp = null;while (true) {if (key.compareTo(h.key) < 0) {// 比当前结点key小,确保当前结点不为2-结点if (!isRed(h.left) && !isRed(h.left.left)) {// 当前结点为2-结点,从兄弟结点借一个结点t = moveRedLeft(h);if (pp != null) {adjustParentLink(h, pp, t);}h = t;}stack.push(h);// 继续遍历左子树pp = h;h = h.left;} else {if (isRed(h.left)) {t = rotateRight(h);if (pp != null) {adjustParentLink(h, pp, t);}h = t;}if (key.compareTo(h.key) == 0 && (h.right == null)) {// 命中叶子结点if (stack.isEmpty()) {// 要删除的为根结点return null;} else {// 非根结点,父链接置空Node p = stack.peek();if (p.left == h) {p.left = null;} else {p.right = null;}}break;}if (!isRed(h.right) && !isRed(h.right.left)) {// 右子树为2-结点,从左子树结点借t = moveRedRight(h);if (pp != null) {adjustParentLink(h, pp, t);}h = t;}if (key.compareTo(h.key) == 0) {// 命中非叶子结点,与后继结点交换Node m = min(h.right);swap(h, m);// 删除替换后的后继结点h.right = deleteMin(h.right);break;}else {// 继续遍历右子树stack.push(h);h = h.right;}}}// 调整删除结点后的二叉树,以满足红黑树的性质Node b;while (!stack.isEmpty()) {h = stack.pop();h.n--;b = balance(h);if (!stack.isEmpty()) {t = stack.peek();adjustParentLink(h, t, b);} else {return b;}}return null;}
6 有序性相关方法
6.1 floor(),ceiling()
- floor() :查找小于等于给定key的最大键
执行流程如下:
- 遍历树,从根结点开始
- 比较key与当前结点key大小cmp
- 如果key等于当前节点key直接返回
- 如果key小于当前结点key,表明要么有,要么在左子树中,继续遍历左子树
- 如果key大于当前结点key,表明当前结点为目前为止小于等于key的最大结点;记录当前结点,继续遍历右子树。
- 循环结束,返回结果
非递归实现如下:
/*** 查找小于等于给定key的最大键* @param key 指定key* @return 小于等于给定key的最大键*/
public K floor(K key) {if (key == null) {throw new IllegalArgumentException("argument to floor() is null");}if (isEmpty()) {throw new NoSuchElementException("calls floor() with empty symbol table");}Node x = floor(root, key);if (x == null) {throw new NoSuchElementException("argument to floor() is too small");} else {return x.key;}
}/*** 查找以x为根结点树中小于等于给定key的最大键* @param key 指定key* @return 小于等于给定key的最大键*/
private Node floor(Node x, K key) {Node t = null;while (x != null) {int cmp = key.compareTo(x.key);if (cmp == 0) {// 名字直接返回return x;} else if (cmp < 0) {// 给定键小于当前结点键,继续遍历左子结点x = x.left;} else {// 目前为止当前结点为小于等于key的最大结点t = x;x = x.right;}}// 返回最终小于等于给定key的最大键return t;
}
注:ceiling()方法同理,代码参考仓库
6.2 rank()
- rank(K key):查找小于key的键的数量
- rank(K key,Node x):查找以x为根结点树小于key的键的数量
rank(K key,Node x)算法思想:
- 如果x为空,返回0
- 比较key与当前结点key的大小,结果cmp
- 如果cmp小于0,查找左子树中小于key的数量
- 如果cmp大于0,计数为:1(当前结点) + 左子树中键的数量+查找右子树中小于key的数量
- 如果相等,计数初始化为左子树中键的数量
非递归实现如下:
/*** 查找小于key的键的数量* @param key 给定的key* @return 小于key的键的数量*/
public int rank(K key) {if (key == null) {throw new IllegalArgumentException("argument to rank() is null");}return rank(key, root);
}/*** 查找以x为根结点小于key的键的数量* 算法:* 当前结点为空,返回0* 比较key与当前结点key大小* 如果key小于当前结点的key,返回:左子树中的小于key的键的数量* 如果key大于当前结点的key,返回:1+当前结点左子树键数量+右子树中小于key的数量* 1 为当前结点* 如果key等于当前节点中的key,返回:当前结点左子树键的数量** @param key 给定的key* @return 小于key的键的数量*/
private int rank(K key, Node x) {// 记录经过的结点Stack<Node> nodes = new Stack<>();// 同步记录下一个结点是左子结点还是右子结点,0表示左,1表示右Stack<Integer> dir = new Stack<>();// 计数int c = 0;while (x != null) {int cmp = key.compareTo(x.key);if (cmp < 0) {// 小于当前结点,记录结点,继续查找左子树nodes.push(x);dir.push(0);x = x.left;} else if (cmp > 0) {// 大于当前结点,记录结点,继续查找右子树nodes.push(x);dir.push(1);x = x.right;} else {// 命中当前结点,计数初始化为左子树结点个数c = size(x.left);break;}}while (!nodes.isEmpty()) {x = nodes.pop();if (dir.pop() == 1) {c += 1 + size(x.left);}}return c;
}
6.3 keys()
- keys(K lo, K hi):位于[lo,hi]之间键的集合
- 算法思想
- 寻找树中位于该范围内左侧临界点
- 按中序遍历判断当前键是否在[lo,hi]范围内,在加入队列;
- 判断当前结点键是否小于最大值hi
- 是,继续遍历后继节点
- 不是,超出范围,结束
源代码如下:
/*** 位于[lo,hi]之间键的集合** @param lo 低位key* @param hi 高位key* @return [lo, hi]之间键的集合*/
public Iterable<K> keys(K lo, K hi) {if (lo == null) {throw new IllegalArgumentException("first argument to keys() is null");}if (hi == null) {throw new IllegalArgumentException("second argument to keys() is null");}Queue<K> queue = new LinkQueue<>();// if (isEmpty() || lo.compareTo(hi) > 0) return queue;keys(root, queue, lo, hi);return queue;
}/*** 以x为根结点树中位于[lo,hi]之间键的集合** @param lo 低位key* @param hi 高位key* @return [lo, hi]之间键的集合*/
private void keys(Node x, Queue<K> queue, K lo, K hi) {Stack<Node> s = new Stack<>();while (x != null || !s.isEmpty()) {while (x != null && lo.compareTo(x.key) < 0) {// 当前结点键大于低位键lo,继续遍历左子树 s.push(x);x = x.left;}if (!s.isEmpty()) {if (x == null) {x = s.pop();}// lo <= x.key <= hi ,加入队列if (lo.compareTo(x.key) <= 0 && hi.compareTo(x.key) >= 0) {queue.offer(x.key);}}if (x != null && hi.compareTo(x.key) > 0) {// 当前结点key小于最大值hi,继续遍历右子树x = x.right;} else {// 当前结点key大于等于最大值hi,结束break;}}
}
到此处,关于算法第四版红黑树主要方法,讲解完毕。下面分析下性能,之后和标准红黑树做下对比。
后记
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10
相关文章:

0202插入删除-算法第四版红黑树-红黑树-数据结构和算法(Java)
文章目录4 插入4.1 序4.2 向单个2-结点插入新键4.3 向树底部的2-结点插入新键4.4 向一棵双键树(3-结点)中插入新键4.5 颜色调整4.6 根结点总是黑色4.7 向树底部的3-结点插入新键4.8 将红链接在树中向上传递4.9 实现5 删除5.1 删除最小键5.2 删除6 有序性…...

vue 生成二维码插件 vue-qr使用方法
一、安装 npm install vue-qr --save二、引入 import VueQr from vue-qrcomponents:{VueQr,},三、使用 <vue-qr:text"dyQrcode":size"170":logoSrc"logo":margin"6":logoScale"0.2"></vue-qr>四、属性说明 …...
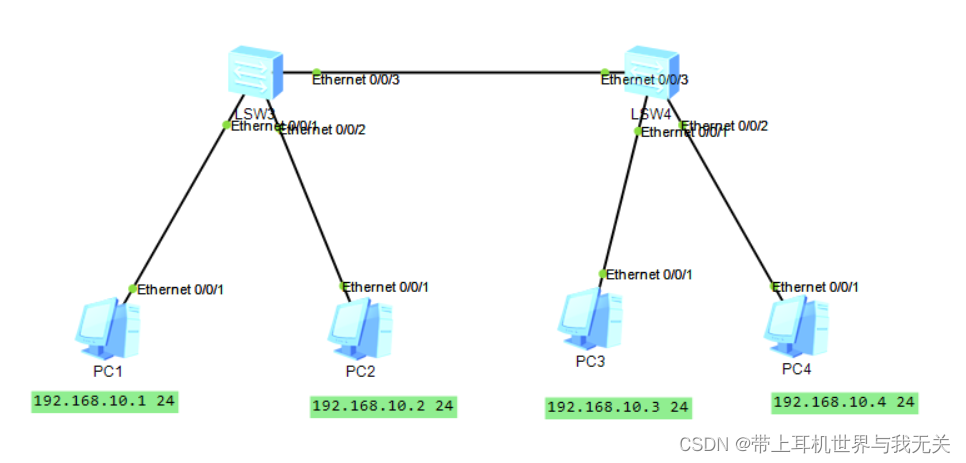
网络工程课(二)
ensp配置vlan 一、配置计算机ip地址和子网掩码 二、配置交换机LSW1 system-view [Huawei]sysname SW1 [SW1]vlan batch 10 20 [SW1]interface Ethernet0/0/1 [SW1-Ethernet0/0/1]port link-type access 将接口设为access接口 [SW1-Ethernet0/0/1]port default vlan 10 [SW1-E…...
: 梯度累加)
Pytorch并行计算(三): 梯度累加
梯度累加 梯度累加(Gradient Accmulation)是一种增大训练时batch size的技巧。当batch size在一张卡放不下时,可以将很大的batch size分解为一个个小的mini batch,分别计算每一个mini batch的梯度,然后将其累加起来优…...
最小覆盖子串(滑动窗口解法))
蓝桥杯入门即劝退(十八)最小覆盖子串(滑动窗口解法)
欢迎关注点赞评论,共同学习,共同进步! ------持续更新蓝桥杯入门系列算法实例-------- 如果你也喜欢Java和算法,欢迎订阅专栏共同学习交流! 你的点赞、关注、评论、是我创作的动力! -------希望我的文章…...

Android一~
进程和线程的区别https://zhuanlan.zhihu.com/p/60375108https://zhuanlan.zhihu.com/p/138689342线程池的用法和原理tcp三次握手和四次挥手、tcp基础http请求报文格式二叉树中序遍历(算法)activity启动模式OKhttp源码讲解Java修饰符Java线程同步的方法s…...

一月券商金工精选
✦研报目录✦ ✦简述✦ 按发布时间排序 国盛证券 “薪火”量化分析系列研究(二)-票据逾期数据中的选股信息 发布日期:2023-01-04 关键词:股票、票据、票据预期 主要内容:本文深入探讨了“票据持续逾期名单”这一…...
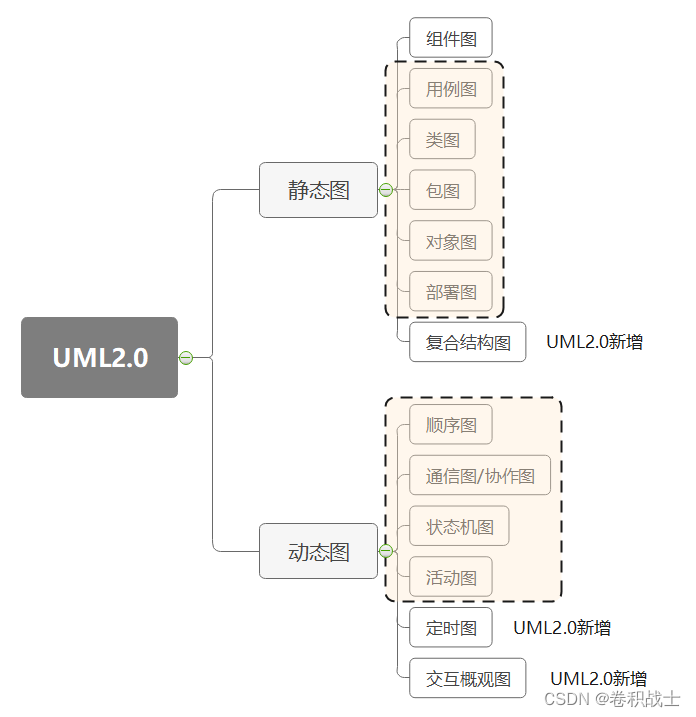
UML中常见的9种图
UML是Unified Model Language的缩写,中文是统一建模语言,是由一整套图表组成的标准化建模语言。UML用于帮助系统开发人员阐明,展示,构建和记录软件系统的产出。通过使用UML使得在软件开发之前, 对整个软件设计有更好的…...
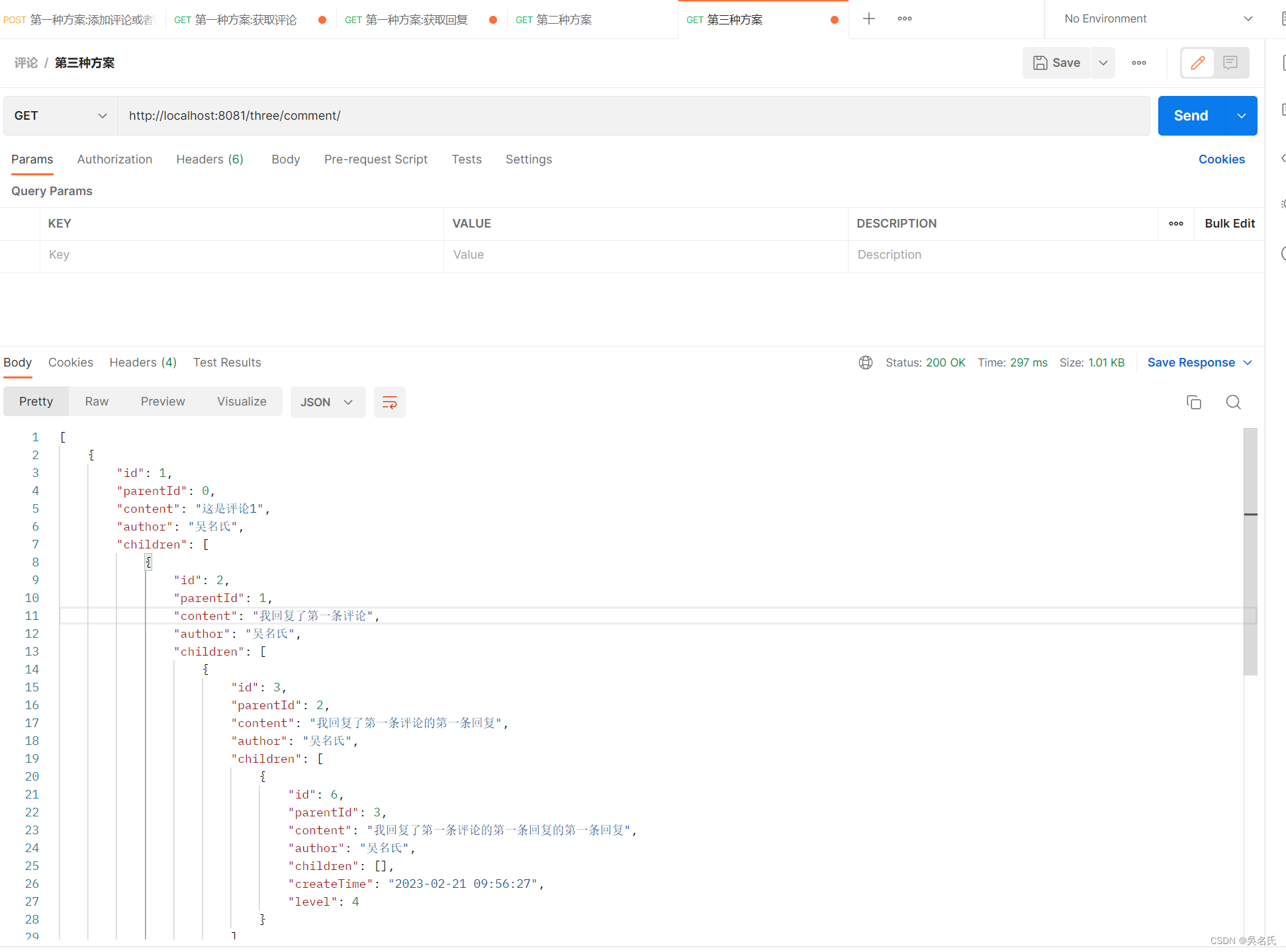
使用SpringBoot实现无限级评论回复功能
评论功能已经成为APP和网站开发中的必备功能。本文采用springbootmybatis-plus框架,通过代码主要介绍评论功能的数据库设计和接口数据返回。我们返回的格式可以分三种方案,第一种方案是先返回评论,再根据评论id返回回复信息,第二种方案是将评论回复直接封装成一个类似于树的数据…...
Kafka 介绍和使用
文章目录前言1、Kafka 系统架构1.1、Producer 生产者1.2、Consumer 消费者1.3、Consumer Group 消费者群组1.4、Topic 主题1.5、Partition 分区1.6、Log 日志存储1.7、Broker 服务器1.8、Offset 偏移量1.9、Replication 副本1.10、Zookeeper2、Kafka 环境搭建2.1、下载 Kafka2.…...
[学习笔记]Rocket.Chat业务数据备份
Rocket.Chat 的业务数据主要存储于mongodb数据库的rocketchat库中,聊天中通过发送文件功能产生的文件储存于/app/uploads中(文件方式设置为"FileSystem"),因此在对Rocket.Chat做数据移动或备份主要分为两步,…...
)
【ZOJ 1090】The Circumference of the Circle 题解(海伦公式+正弦定理推论)
计算圆的周长似乎是一项简单的任务——只要你知道它的直径。但如果你没有呢? 我们给出了平面中三个非共线点的笛卡尔坐标。 您的工作是计算与所有三个点相交的唯一圆的周长。 输入规范 输入文件将包含一个或多个测试用例。每个测试用例由一条包含六个实数x1、y1、x…...

【go】slice原理
slice包含3个部分: 1.内存的起始位置 2.切片的大小(已经存放的元素数量) 3.容量(可以存放的元素数量) 使用make初始化切片会开辟底层内存,并初始化元素值为默认值,如数字为0,字符串为空 使用New初始化切片不会开辟底层数组&…...
,真的很详细,一篇文章你就会了)
【数据库】MySQL概念知识语法-基础篇(DQL),真的很详细,一篇文章你就会了
目录通用语法及分类DQL(数据查询语言)基础查询条件查询聚合查询(聚合函数)分组查询排序查询分页查询内连接查询外连接查询自连接查询联合查询子查询列子查询行子查询表子查询总结通用语法及分类 ● DDL: 数据定义语言,…...
博客界的至高神:属于自己的WordPress网站,你值得拥有!
【如果暂时没时间安装,可以直接跳转到最后先看展示效果】 很多朋友都想有一个对外展示的窗口,在那里放一些个人的作品或者其他想对外分享的东西。大部分人选择了在微博、公众号等平台,毕竟这些平台流量大,我们可以很轻易地把自己…...
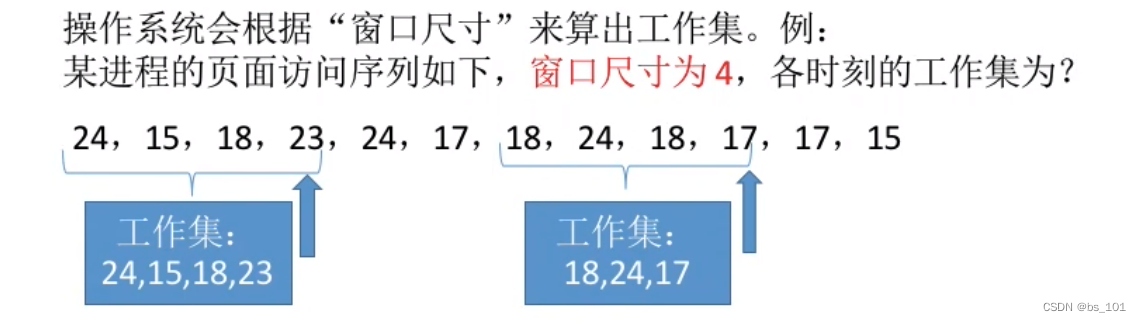
操作系统(day13)-- 虚拟内存;页面分配策略
虚拟内存管理 虚拟内存的基本概念 传统存储管理方式的特征、缺点 一次性: 作业必须一次性全部装入内存后才能开始运行。驻留性:作业一旦被装入内存,就会一直驻留在内存中,直至作业运行结束。事实上,在一个时间段内&…...
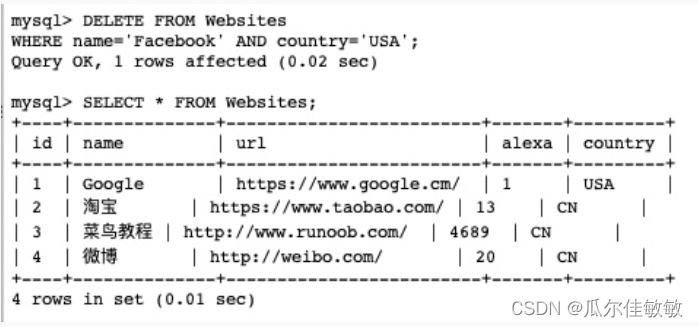
SQL零基础入门学习(四)
SQL零基础入门学习(三) SQL INSERT INTO 语句 INSERT INTO 语句用于向表中插入新记录。 SQL INSERT INTO 语法 INSERT INTO 语句可以有两种编写形式。 第一种形式无需指定要插入数据的列名,只需提供被插入的值即可: INSERT …...
19岁就患老年痴呆!这些前兆别忽视!
在大部分人的印象中,阿尔兹海默症好像是专属于老年人的疾病,而且它的另一个名字就是老年痴呆症。然而,前不久,一位19岁的男生患上了阿尔兹海默症,是迄今为止最年轻的患者。这个男生从17岁开始,就出现了注意…...
【C++】thread|mutex|atomic|condition_variable
本篇博客,让我们来认识一下C中的线程操作 所用编译器:vs2019 阅读本文前,建议先了解线程的概念 👉 线程概念 1.基本介绍 在不同的操作系统,windows、linux、mac上,都会对多线程操作提供自己的系统调用接口…...
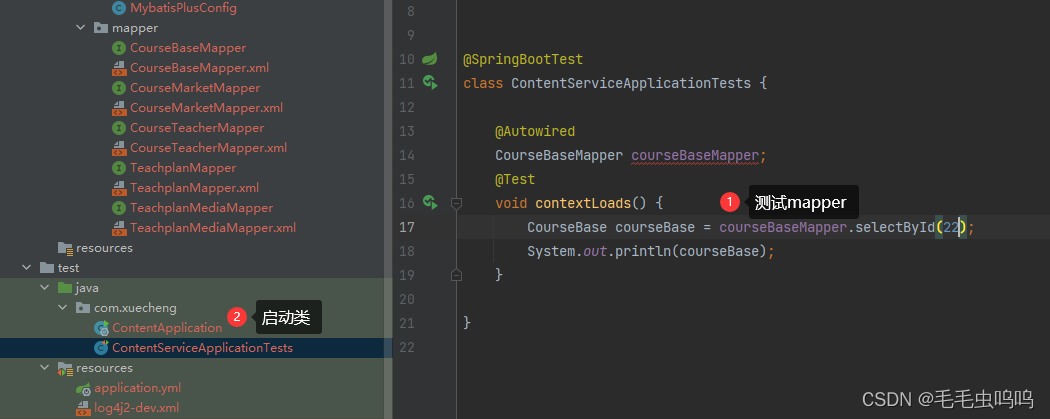
学成在线项目笔记
业务层开发 DAO开发示例 生成实体类对应的mapper和xml文件 定义MybatisPlusConfig,用于扫描mapper和配置分页拦截器 MapperScan("com.xuecheng.content.mapper") Configuration public class MybatisPlusConfig {Beanpublic MybatisPlusInterceptor myb…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
