数学建模:拟合算法
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛
数学建模:拟合算法
文章目录
- 数学建模:拟合算法
- 拟合算法
- 多项式拟合
- 非线性拟合
- cftool工具箱的使用
拟合算法
根据1到12点间的温度数据求出温度与时间之间的近似函数关系 F ( t ) F(t) F(t),由 F ( t ) F(t) F(t) 推断 t =13.5 时的温度。这种根据离散数据求数据间近似函数关系的问题称为曲线拟合问题。
拟合问题与插值问题的区别在于:
- 插值函数过已知点,而拟合函数不一定过已知点.
- 插值主要用于求函数值,而拟合的主要目的是求函数关系,从而进行预测等进一步的分析。
多项式拟合
[p,S] = polyfit(x,y,n);
x和y是被拟合数据的自变量和因变量;n为拟合多项式的次数;a为拟合多项式系数构成的向量;S为 分 析 拟 合 效 果 所需的指标(可省略)。
%% 多项式拟合,使用cftool工具箱
clc;clear;
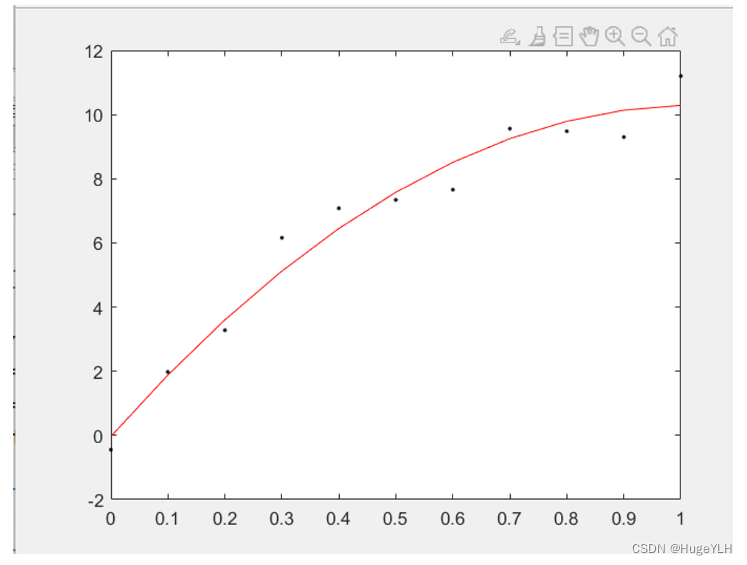
x=0:0.1:1;
y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];
%%
[p,~] = polyfit(x,y,2);
xp = 0:0.1:1;
yp = polyval(p,xp);
plot(x,y,'.k',xp,yp,'r');
非线性拟合
clc;clear;
% 指定函数拟合步骤
% (1) 输入待拟合数据x,y
%(2)指定函数关系式
syms t;
x=[0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15];
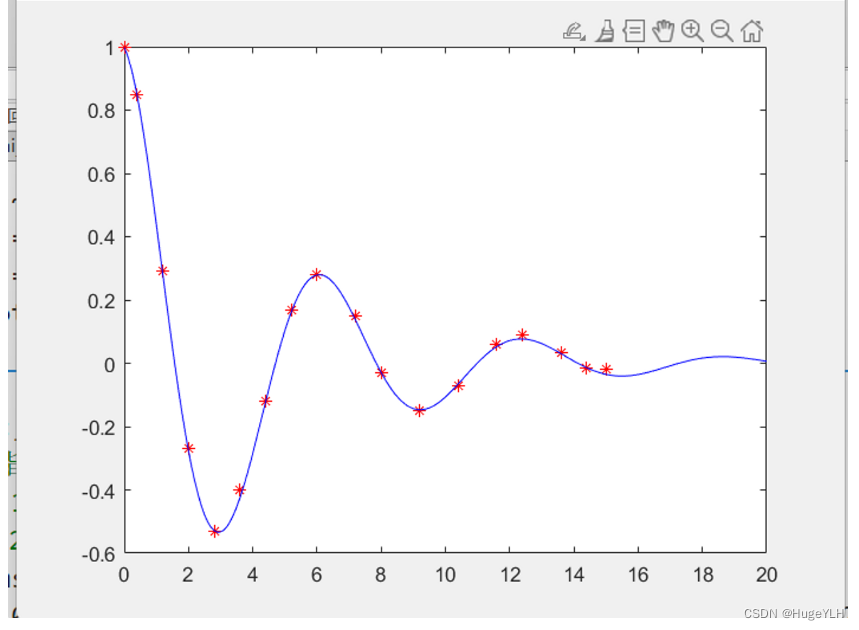
y=[1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.09;0.032;-0.015;-0.02];%指定函数形式为f(t)=acos(kt)e^(wt),进行拟合
f=fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{'a','k','w'});
cfun=fit(x,y,f) %显示拟合函数
xi=0:.1:20;
yi=cfun(xi);
plot(x,y,'r*',xi,yi,'b-');
cftool工具箱的使用
26 老哥带你学数模—拟合算法原理及案例分析(P47-P74).pdf
相关文章:

数学建模:拟合算法
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:拟合算法 文章目录 数学建模:拟合算法拟合算法多项式拟合非线性拟合cftool工具箱的使用 拟合算法 根据1到12点间的温度数据求出温度与时间之间的近似函数关系 F ( t ) F(…...

计算机网络-笔记-汇总
目录 📚 前言 🌸章节汇总 🚀 学习心得 ⌛2023年8月31日 星期四 📚 前言 在学习了【操作系统】、【计算机组成原理】之后 再来学习【计算机网络】,对计算机之间如何通信,有了一个大致的认识。 可以想象…...
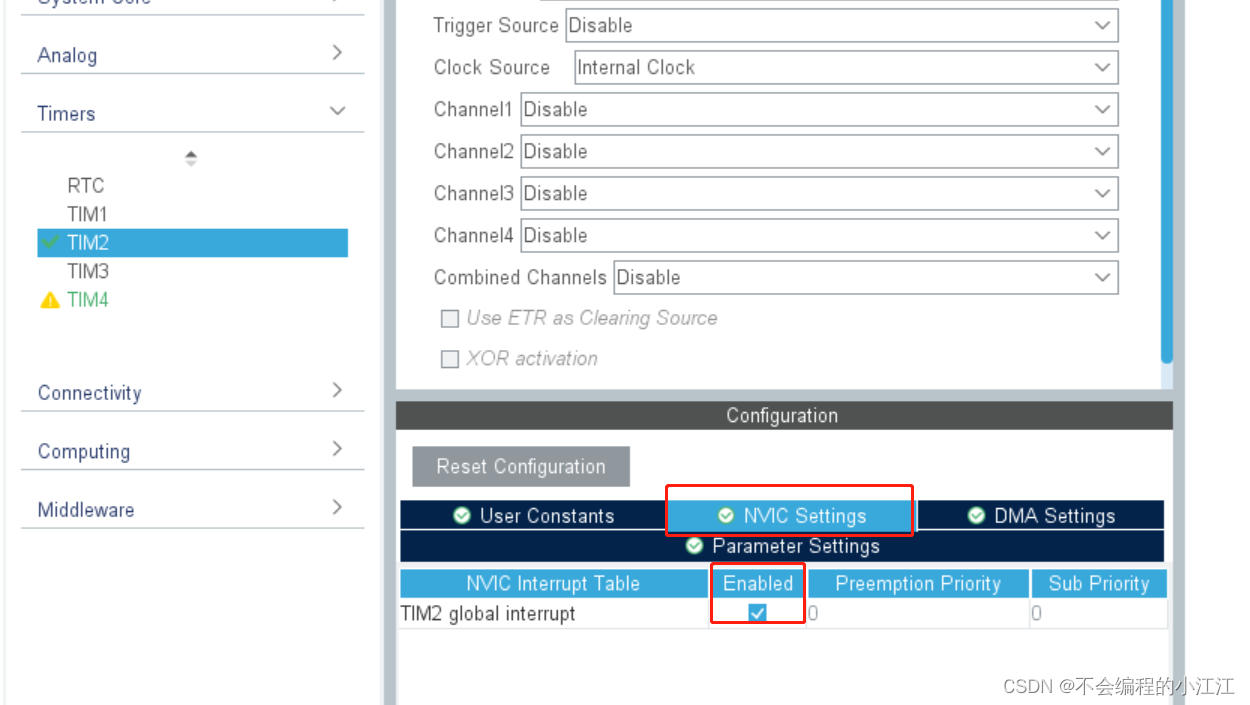
STM32定时器定时及其应用
STM32定时器定时及其应用 定时器概述☆定时器相关配置CubeMX工程配置及程序实现固件库程序设计及实现 定时器概述 1. 工作原理 使用精准的时基,通过硬件的方式,实现定时功能。定时器核心就是计数器 2. 定时器分类 基本定时器(TIM6~TIM7…...
 游游的字符重排(next_permutation的使用))
(牛客) 游游的字符重排(next_permutation的使用)
题目描述 游游定义一个字符串是“好串”,当且仅当该字符串相邻的字符不相等。例如"arcaea"是好串,而"food"不是好串。 游游拿到了一个字符串,她可以将该字符串的各个字符顺序随意打乱。她想知道一共可以生产多少种不同的…...
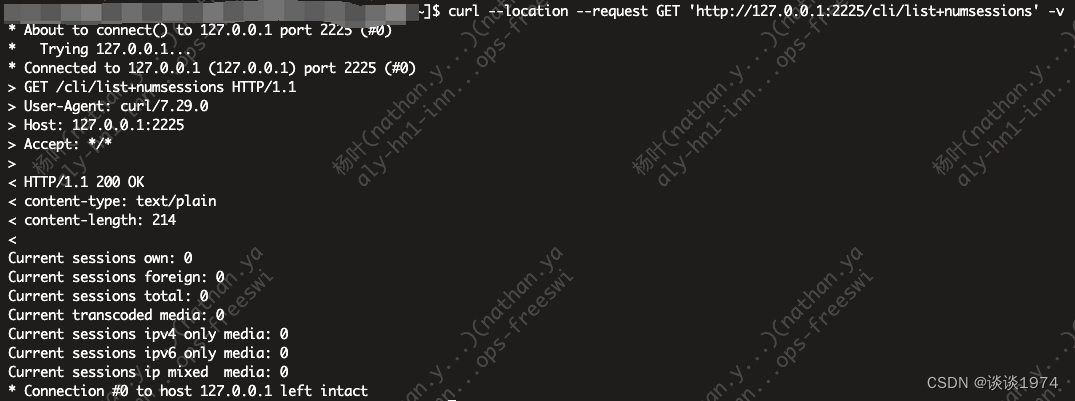
RTPEngine 通过 HTTP 获取指标的方式
文章目录 1.背景介绍2.RTPEngine 支持的 HTTP 请求3.通过 HTTP 请求获取指标的方法3.1 脚本配置3.2 请求方式 1.背景介绍 RTPEngine 是常用的媒体代理服务器,通常被集成到 SIP 代理服务器中以减小代理服务器媒体传输的压力,其架构如下图所示。这种使用方…...

聚鑫数藏平台——引领数字资产管理新风向
随着数字经济的飞速发展,新金融生态应运而生。区块链技术的崭新突破,使数字资产的重要性日益凸显,为投资者带来了前所未有的机遇和挑战。在此背景下,聚鑫数藏平台横空出世,引领着数字资产管理的新风向。 聚鑫数藏平台&…...

web3j solidity 转java
需要使用的环境 web3j,nodejs 安装编译sol工具 1 $ npm install -g solc 保存为hello.sol文件到本地 1 2 3 4 5 6 7 8 pragma solidity 0.4.19; contract hello { function main(uint a) constant returns (uint b) { uint result a * 8; …...

uniapp项目实战系列(3):底部导航栏与头部导航栏的配置
目录 系列往期文章(点击跳转)uniapp项目实战系列(1):导入数据库,启动后端服务,开启代码托管(点击跳转)uniapp项目实战系列(2):新建项目,项目搭建,微信开发工具…...

Jwt工具类
导入依赖 <dependency><groupId>io.jsonwebtoken</groupId><artifactId>jjwt</artifactId><version>0.9.1</version> </dependency> <dependency><groupId>javax.xml.bind</groupId><artifactId>jax…...

计算机网络-笔记-第五章-运输层
🌸章节汇总 一、第一章——计算机网络概述 二、第二章——物理层 三、第三章——数据链路层 四、第四章——网络层 五、第五章——运输层 六、第六章——应用层 目录 五、第五章——运输层 1、运输层概述 2、运输层端口号、复用、分用 (1࿰…...
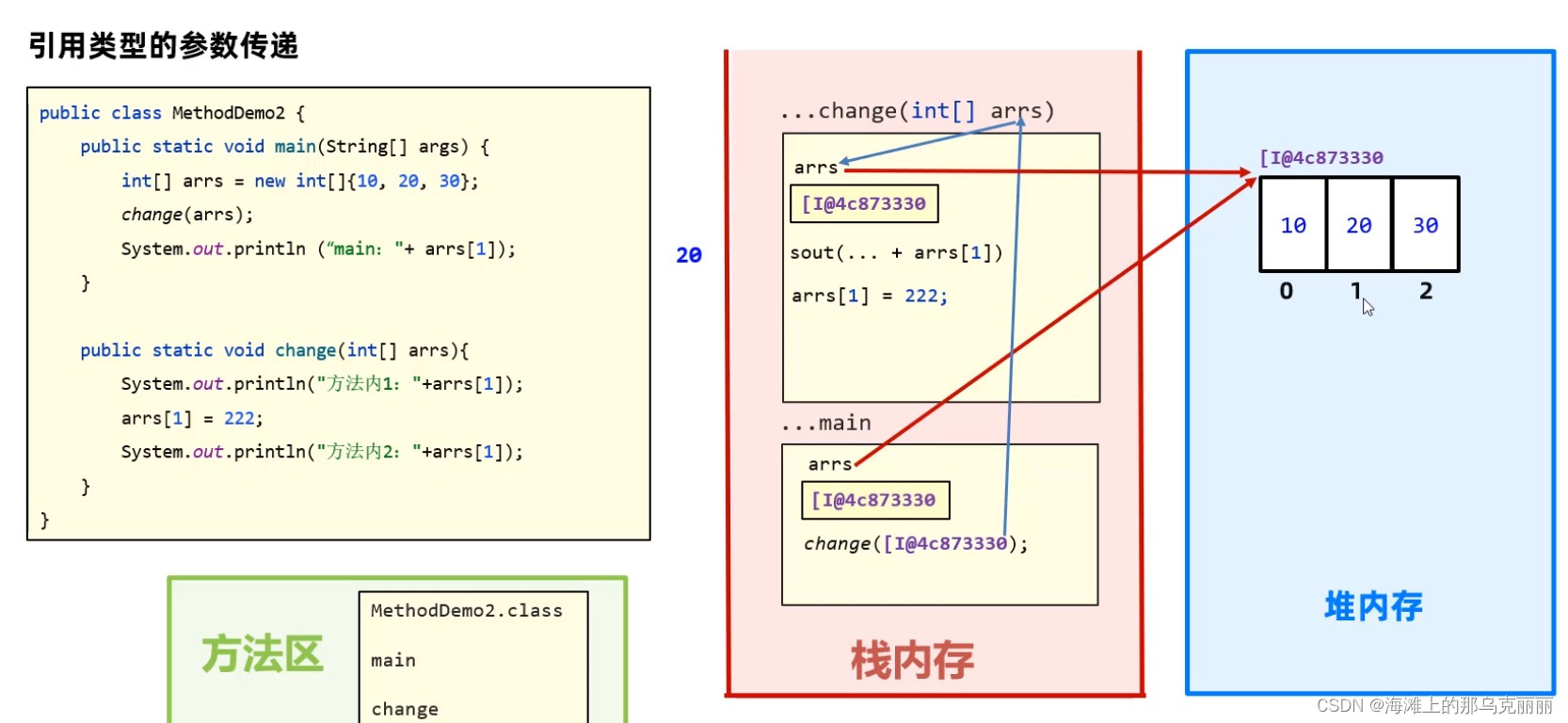
java-参数传递机制
java参数传递机制都是值传递。 基本类型参数传输都是数据值。 传递到方法中的值是拷贝后的值。 引用类型参数传输的都是地址值。 如果是数组的参数传递,那么是引用传递(本质上还是值传递,但是由于数组的值传递是传递数组的内存地址…...

Python编程练习与解答 练习96:字符串是否表示整数
本练习将编写一个名为isInteger的函数,用于确定字符串中的字符是否代表有效整数,确定字符串是否表示整数时,则应忽略开通要或者结尾的任何空白。一旦这个空白被忽略,如果字符串的长度至少是1,且只包含数字,…...

Scala的特质trait与java的interface接口的区别,以及Scala特质的自身类型和依赖注入
1. Scala的特质trait与java接口的区别 Scala中的特质(trait)和Java中的接口(interface)在概念和使用上有一些区别: 默认实现:在Java中,接口只能定义方法的签名,而没有默认实现。而在…...

检查js中的字符串是否可以成为回文
探索 JavaScript 中的字符串操作领域揭示了一个令人着迷的挑战:确定给定的字符串是否可以转换为回文。回文,即正反读相同的单词或短语,具有固有的吸引力,并激发了寻求揭开其神秘属性的开发人员的好奇心。在本文中,我们…...

时序预测 | MATLAB实现CNN-LSTM卷积长短期记忆神经网络时间序列预测(风电功率预测)
时序预测 | MATLAB实现CNN-LSTM卷积长短期记忆神经网络时间序列预测(风电功率预测) 目录 时序预测 | MATLAB实现CNN-LSTM卷积长短期记忆神经网络时间序列预测(风电功率预测)预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1…...
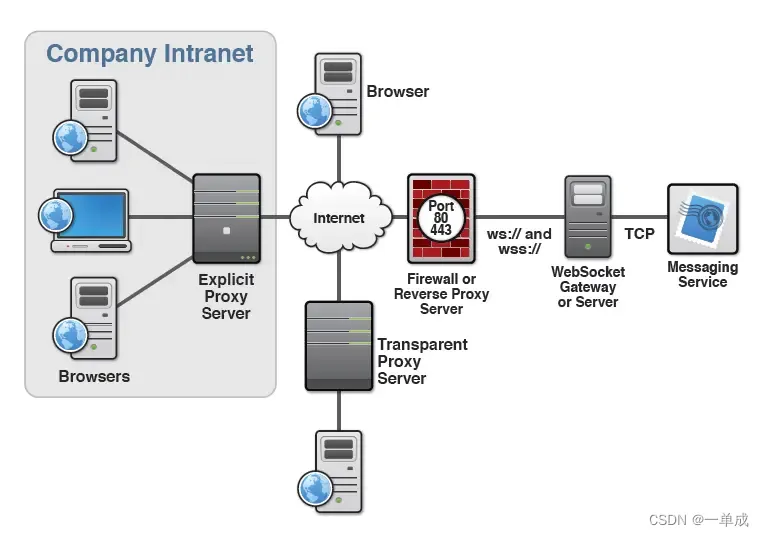
WebSocket--技术文档--基本概念--《快速了解WebSocket协议》
阿丹: 不断学习新技术,丰富自己了解更多才能扩展更多世界可能。 官网 WebSocket首页、文档和下载 - HTML5开发相关 - OSCHINA - 中文开源技术交流社区 软件简介 WebSocket 是 HTML5 开始提供的一种浏览器与服务器间进行全双工通讯的网络技术。 WebS…...
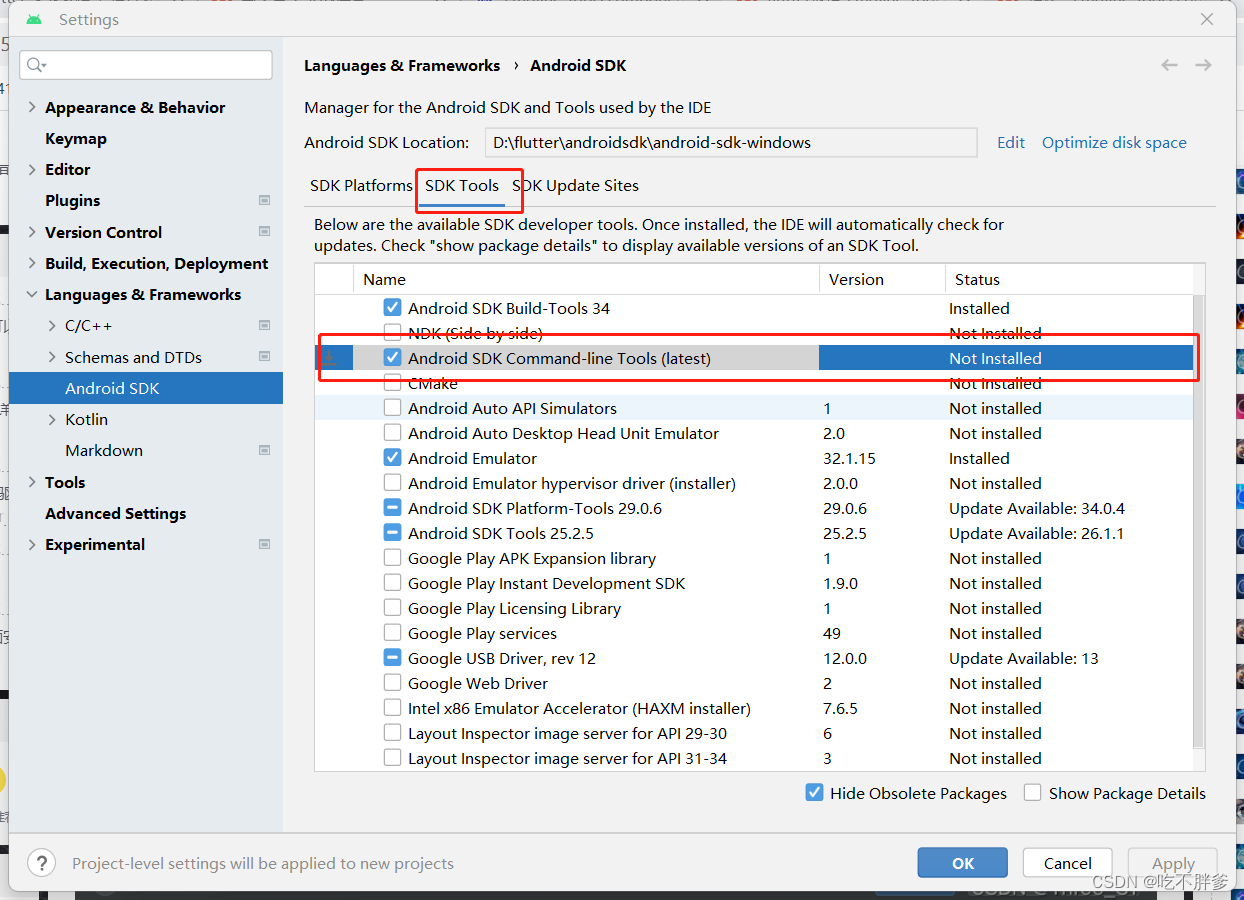
flutter报错-cmdline-tools component is missing
安装完androidsdk和android studio后,打开控制台,出现错误 解决办法 找到自己安装android sdk的位置,然后安装上,并将下面的勾选上 再次运行 flutter doctor 不报错,出现以下画面 Doctor summary (to see all det…...
torch.bmm功能解读
bmm 是 batched matrix multiple 的简写,即批量矩阵乘法,矩阵是二维的,加上batch一个维度,因此该函数的输入必须是两个三维的 tensor,三个维度代表的含义分别是:(批量,行,…...

如何使用Puppeteer进行金融数据抓取和预测
导语 Puppeteer是一个基于Node.js的库,可以用来控制Chrome或Chromium浏览器,实现网页操作、截图、PDF生成等功能。本文将介绍如何使用Puppeteer进行金融数据抓取和预测,以及如何使用亿牛云爬虫代理提高爬虫效果。 概述 金融数据抓取是指从…...

Linux下 Socket服务器和客户端文件互传
目录 1.项目描述 2.函数准备 2.1 gets函数 2.2 popen函数、fread函数 2.3 access 函数 2.4 exit 函数 2.5 strtok 函数 2.6 chdir函数 3.项目代码 3.1服务器代码 3.2客户端代码 4.问题总结 1.项目描述 基于Soket聊天服务器,实现服务器和客户端的文件传输。…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
