球球的排列
题目传送门
引
计数DP,好像特别经典,有两种做法,我只会 O ( n 3 ) O(n^3) O(n3),有 O ( n 2 ) O(n^2) O(n2)的
解法
首先, 若 x y = p 2 且 x z = q 2 , 则 y z = ( p q x ) 2 若xy=p^2且xz=q^2,则yz=(\frac{pq}{x} )^2 若xy=p2且xz=q2,则yz=(xpq)2 所以题目中给出的关系具有传递性,故先预处理,不可相邻的球分在一个组
为了方便,下面叫同一组的球为同色
伪代码如下:
bool check(ll x){ll tmp=sqrt(x);return (tmp*tmp==x);
}for(int i=1;i<=n;i++) {a[i]=read(),b[i]=i;for(int j=1;j<i;j++) {if(check(1ll*a[i]*a[j])) {b[i]=j;break;}}
}
接下来,
设计状态
首先我们无脑枚举一维 i i i表示前 i i i个球,注意同色的球排序后的序列是连续的
观察题目的限制相当于同色的球不能相邻,设计后两维要考虑好同色和相邻
f i , j , . k : 前 i 个球,共有 j + k 对相邻的球同色,其中 j 对跟第 i 个球异色, k 对同色 f_{i,j,.k}:前i个球,共有j+k对相邻的球同色,其中j对跟第i个球异色,k对同色 fi,j,.k:前i个球,共有j+k对相邻的球同色,其中j对跟第i个球异色,k对同色
那么最后的答案 a n s = f n , 0 , 0 ans=f_{n,0,0} ans=fn,0,0
设计出了状态其实就成功了一半,但这道题的转移也很毒瘤,客官且看
状态转移
考虑 f i f_i fi与 f i − 1 f_{i-1} fi−1的关系, f i f_i fi的状态都是由 i − 1 i-1 i−1个球的 i i i个空隙插入一个球而来的
那么第 i i i个球与第 i − 1 i-1 i−1个球有两种关系:a.同色;b.异色
第 i i i个球插入的位置也有两种可能:c.插入两个同色球之间;d.插入两个异色球之间
所以对6种可能分别考虑转移:
1. a与c
发现,此时前 i − 1 i-1 i−1个球已有与 i i i同色的,那么明显第 i i i个球放在与其同色的球旁边转移不同,设排列中已有 c n t cnt cnt个球与 i i i同色,此时有:
f i , j , k = f i − 1 , j , k − 1 ∗ ( c n t ∗ 2 − ( k − 1 ) ) f_{i,j,k}=f_{i-1,j,k-1}*(cnt*2-(k-1)) fi,j,k=fi−1,j,k−1∗(cnt∗2−(k−1))
然后第 i i i个球插入的位置是与自己异色的球间,让 j j j减少了1,此时有:
f i , j , k = f i − 1 , j + 1 , k ∗ ( j + 1 ) f_{i,j,k}=f_{i-1,j+1,k}*(j+1) fi,j,k=fi−1,j+1,k∗(j+1)
2.a与d
减去前两种情况,还剩 i − c n t ∗ 2 + k − j i-cnt*2+k-j i−cnt∗2+k−j种情况, j , k j,k j,k不变,此时有:
f i , j , k = f i − 1 , j , k ∗ ( i − c n t ∗ 2 + k − j ) f_{i,j,k}=f_{i-1,j,k}*(i-cnt*2+k-j) fi,j,k=fi−1,j,k∗(i−cnt∗2+k−j)
3.b与c
可知第 i i i个球的颜色是首次出现,故 k k k=0,让 ( j + k ) (j+k) (j+k)减少了1,所以要枚举 j ‘ j‘ j‘和 k ’ k’ k’,有:
f i , j , 0 = ∑ j ′ + k ′ = j + 1 f i , j ′ , k ′ ∗ ( j + 1 ) f_{i,j,0}=\sum_{j'+k'=j+1} f_{i,j',k'} *(j+1) fi,j,0=j′+k′=j+1∑fi,j′,k′∗(j+1)
4.b与d
对 j , k j,k j,k不产生影响,枚举即可,此时有:
f i , j , 0 = ∑ j ′ + k ′ = j f i , j ′ , k ′ ∗ ( i − j ) f_{i,j,0}=\sum_{j'+k'=j} f_{i,j',k'}*(i-j) fi,j,0=j′+k′=j∑fi,j′,k′∗(i−j)
代码实现倒是简单,放一下
code:
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 3e2 + 5,mod=1e9+7;
int n,cnt;
int f[2][N][N],a[N],b[N];
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();return x*f;
}
bool check(ll x){ll tmp=sqrt(x);return (tmp*tmp==x);
}
int main() {n=read();for(int i=1;i<=n;i++) {a[i]=read(),b[i]=i;for(int j=1;j<i;j++) {if(check(1ll*a[i]*a[j])) {b[i]=j;break;}}}sort(b+1,b+1+n);f[0][0][0]=1;for(int i=1;i<=n;i++,cnt++) {int now=i&1,pre=now^1;memset(f[now],0,sizeof f[now]);if(b[i]==b[i-1]){for(int j=0;j<i;j++) {for(int k=0;k<=cnt;k++){if(k) f[now][j][k]=(1ll*f[now][j][k]+1ll*f[pre][j][k-1]*(cnt*2-(k-1)))%mod;f[now][j][k]=(1ll*f[now][j][k]+1ll*f[pre][j+1][k]*(j+1))%mod;f[now][j][k]=(1ll*f[now][j][k]+1ll*f[pre][j][k]*(i-cnt*2+k-j))%mod;}}}else {cnt=0;for(int j=0;j<i;j++){for(int k=0;k<=j+1;k++){if(k<=j) f[now][j][0]=(1ll*f[now][j][0]+1ll*f[pre][k][j-k]*(i-j))%mod;f[now][j][0]=(1ll*f[now][j][0]+1ll*f[pre][k][(j+1)-k]*(j+1))%mod;}}}}printf("%d\n",f[n&1][0][0]);
}
TXL
相关文章:

球球的排列
题目传送门 引 计数DP,好像特别经典,有两种做法,我只会 O ( n 3 ) O(n^3) O(n3),有 O ( n 2 ) O(n^2) O(n2)的 解法 首先, 若 x y p 2 且 x z q 2 , 则 y z ( p q x ) 2 若xyp^2且xzq^2,则yz(\frac{pq}{x} )^2 若xyp2且xzq2,则yz(xpq…...
1783_CMD启动MATLAB同时执行一个脚本
全部学习汇总: GitHub - GreyZhang/g_matlab: MATLAB once used to be my daily tool. After many years when I go back and read my old learning notes I felt maybe I still need it in the future. So, start this repo to keep some of my old learning notes…...

C语言中内存分配的几种方式
目录 C语言中内存分配的几种方式静态内存分配栈内存分配堆内存分配内存映射文件 C语言中内存分配的几种方式 静态内存分配 静态内存分配是在程序编译时分配内存,通常用于全局变量和静态变量。这些变量的内存空间在程序的整个运行期间都是存在的。 栈内存分配 栈内存…...
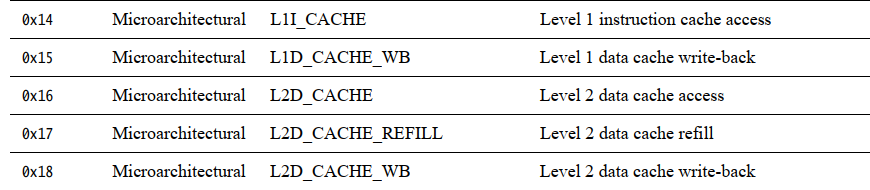
组相联cache如何快速实现cache line eviction并使用PMU events验证
如何快速实现cache line eviction 一,什么是cache hit、miss、linefill、evict ?1.1 如果要程序员分别制造出cache hit、miss、linefill、evict这四种场景,该怎么做? 二,实现cache line eviction的方法1.1 直接填充法3…...
【Stable Diffusion安装】支持python3.11 window版
前言 主要的安装步骤是参考B站播放量第一的视频,但是那位阿婆主应该是没有编程经验,只强调使用3.10,而python最新版本是3.11。 理论上来说,只是一个小版本的不同,应该是可以安装成功了。自己摸索了下,挺费…...

Anycloud37D平台移植wirelesstools
0. 环境准备 下载 :https://www.linuxfromscratch.org/blfs/view/svn/basicnet/wireless_tools.html 1. 交叉编译wireless_tools tar xzf wireless_tools.29.tar.gz cd wireless_tools.29/打开Makefile,修改配置: ## Compiler to use (mo…...

海康机器人工业相机 Win10+Qt+Cmake 开发环境搭建
文章目录 一. Qt搭建海康机器人工业相机开发环境 一. Qt搭建海康机器人工业相机开发环境 参考这个链接安装好MVS客户端 Qt新建一个c项目 cmakeList中添加海康机器人的库,如下: cmake_minimum_required(VERSION 3.5)project(HIKRobotCameraTest LANG…...
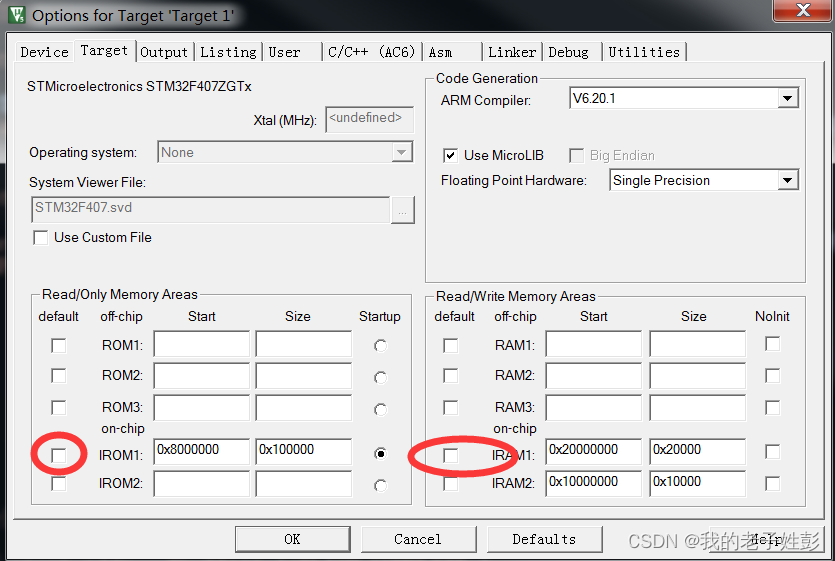
使用MDK5的一些偏僻使用方法和谋个功能的作用
程序下载后无法运行 需要勾选如下库,是优化后的库; MicroLib和标准C库之间的主要区别是: 1、MicroLib是专为深度嵌入式应用程序而设计的。 2、MicroLib经过优化,比使用ARM标准库使用更少的代码和数据内存。 3、MicroLib被设计成在没有操作…...
【实战】十一、看板页面及任务组页面开发(六) —— React17+React Hook+TS4 最佳实践,仿 Jira 企业级项目(二十八)
文章目录 一、项目起航:项目初始化与配置二、React 与 Hook 应用:实现项目列表三、TS 应用:JS神助攻 - 强类型四、JWT、用户认证与异步请求五、CSS 其实很简单 - 用 CSS-in-JS 添加样式六、用户体验优化 - 加载中和错误状态处理七、Hook&…...

在 Amazon 搭建无代码可视化的数据分析和建模平台
现代企业常常会有利用数据分析和机器学习帮助解决业务痛点的需求。如制造业中,利用设备采集上来的数据做预测性维护,质量控制;在零售业中,利用客户端端采集的数据做渠道转化率分析,个性化推荐等。 亚马逊云科技开发者…...

Pinely Round 2 (Div. 1 + Div. 2) G. Swaps(组合计数)
题目 给定一个长度为n(n<1e6)的序列,第i个数ai(1<ai<n), 操作:你可以将当前i位置的数和a[i]位置的数交换 交换可以操作任意次,求所有本质不同的数组的数量,答案对1e97取模 思路来源 力扣群 潼神 心得 感…...

elasticSearch+kibana+logstash+filebeat集群改成https认证
文章目录 一、生成相关证书二、配置elasticSearh三、配置kibana四、配置logstash五、配置filebeat六、连接https es的java api 一、生成相关证书 ps:主节点操作 切换用户:su es 进入目录:cd /home/es/elasticsearch-7.6.2 创建文件&#x…...

GPT带我学-设计模式-迭代器模式
1 什么是迭代器设计模式? 迭代器设计模式是一种行为型设计模式,用于提供一种统一的方式来遍历一个集合对象中的元素,而不需要暴露该对象的内部结构。它将集合对象的遍历操作与集合对象本身分离开来,使得遍历操作可以独立于集合对…...
的Python实现)
数学建模--层次分析法(AHP)的Python实现
目录 1.算法流程简介 2.算法核心代码 3.算法效果展示 1.算法流程简介 """ AHP:层次分析法,层次分析法还是比较偏向于主观的判断的,所以在建模的时候尽可能不要去使用层次分析法 不过在某些创新的评价方法上,也是能够运用层次分析使得评价变得全面一些,有可…...

机器学习笔记之最优化理论与方法(三)凸集的简单认识(下)
机器学习笔记之最优化理论与方法——凸集的简单认识[下] 引言回顾:基本定义——凸集关于保持集合凸性的运算仿射变换 凸集基本性质:投影定理点与凸集的分离支撑超平面定理 引言 继续凸集的简单认识(上)进行介绍,本节将介绍凸集的基本性质以及…...
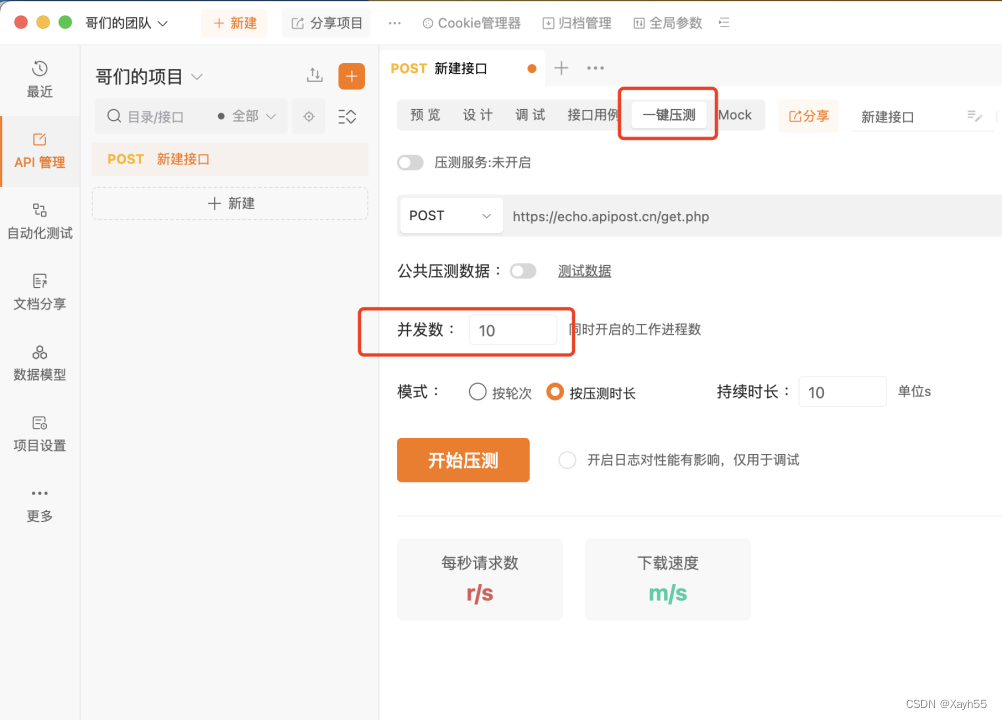
Apipost:API文档、调试、Mock与测试的一体化协作平台
随着数字化转型的加速,API(应用程序接口)已经成为企业间沟通和数据交换的关键。而在API开发和管理过程中,API文档、调试、Mock和测试的协作显得尤为重要。Apipost正是这样一款一体化协作平台,旨在解决这些问题…...

Homebrew下载安装及使用教程
Homebrew是什么? 简单来说,就是用命令行的形式去管理mac系统的包或软件。 安装命令 /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)"国内请使用镜像源进行下载 执行上述命令后会要求输入…...

【Codeforces】CF193D Two Segments
题目链接 CF方向 Luogu方向 题目解法 考虑在值域上的问题:有多少段区间,对应在排列上不超过 2 2 2 段 肯定需要枚举一个端点,另一个快速算出,考虑枚举值域区间右端点 r r r,计算 l l l 可以发现,新增…...

内存管理概述
前言 在学习计算机科学时,内存管理是一个非常重要的概念。简单地说,内存是计算机用来存储和访问数据的地方。而内存管理是计算机系统如何分配、使用和管理内存的过程。 为什么要学习内存管理? 1. 高效性:内存管理能够帮助计算机更…...
Spring的重试机制-SpringRetry
在我们的日常开发中,经查会遇到调用接口失败的情况,这时候就需要通过一些方法来进行重试,比如通过while循环手动重复调用或,或者通过记录错误接口url和参数到数据库,然后手动调用接口,或者通过JDK/CGLib动态…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...

【阅读笔记】MemOS: 大语言模型内存增强生成操作系统
核心速览 研究背景 研究问题:这篇文章要解决的问题是当前大型语言模型(LLMs)在处理内存方面的局限性。LLMs虽然在语言感知和生成方面表现出色,但缺乏统一的、结构化的内存架构。现有的方法如检索增强生成(RA…...
