数学建模--整数规划匈牙利算法的Python实现
目录
1.算法流程简介
2.算法核心代码
3.算法效果展示
1.算法流程简介
#整数规划模型--匈牙利算法求解
"""
整数规划模型及概念:规划问题的数学模型一般由三个因素构成 决策变量 目标函数 约束条件;线性规划即以线性函数为目标函数,线性条件为约束条件;如果一个线性规划模型中的部分或全部决策变量取整数值,则称该线性规划模型为整数线性规划模型,除此还有非线性整数规划。
整数规划的几种类型:1:纯整数规划:全部决策变量都必须取整数值的整数规划模型;2:混合整数规划:决策变量中有一部分必须取整数值,另一部分可以不取整数值的整数规划模型;3:0-1整数规划:决策变量只能取0或1的整数规划。
匈牙利算法基本思路:对费用矩阵C的行和列减去某个常数,将C化为有n个位于不同行不同列的零元素,令这些零元素对应的变量取1,其余变量取0,即得到指派问题的最优解。匈牙利法是基于指派问题的标准型的,标准型需满足以下3个条件:(1)目标函数求min;(2)效率矩阵为n阶方阵;(3)效率矩阵中所有的元素Cij>=0,且为常数
处理效率矩阵的原则:匈牙利算法的本质工作就是处理效率矩阵,时期变的符合一定的输入要求最终效果:效率矩阵通过一定的变换之后,每行每列都至少存在一个0,记这个矩阵为B。1.如果行列本身就有0,该行列不需要处理2.如果某行没有0,寻找到该行的min元素,此行都减去min。3.如果某列没有0,寻找到该列的min元素,此列都减去min。
"""2.算法核心代码
#开始求解整数规划问题
from scipy.optimize import linear_sum_assignment
import numpy as np
#1.导入cost/效率矩阵:
cost_arr=np.array([[4,1,3],[2,0,5],[3,2,2]])
n=len(cost_arr)
row_best,col_best=linear_sum_assignment(cost_arr)
print("开销矩阵最优行索引解:",row_best)
print("开销矩阵最优列索引解:",col_best)
#求解最优解:
ans=0
best_ans=[]
for i in range(n):ans+=cost_arr[row_best[i]][col_best[i]]best_ans.append(cost_arr[row_best[i]][col_best[i]])
print("最优解由",n,"个数据进行组成")
for i in range(n):print("第",i+1,"个数据是位于开销矩阵第",row_best[i],"行第",col_best[i],"列的值:",cost_arr[row_best[i]][col_best[i]])
print("综上所示本题最优解组成是:",best_ans)
print("本题规划的最优解是:",ans)3.算法效果展示

相关文章:

数学建模--整数规划匈牙利算法的Python实现
目录 1.算法流程简介 2.算法核心代码 3.算法效果展示 1.算法流程简介 #整数规划模型--匈牙利算法求解 """ 整数规划模型及概念:规划问题的数学模型一般由三个因素构成 决策变量 目标函数 约束条件;线性规划即以线性函数为目标函数&a…...
OpenCV(十三):图像中绘制直线、圆形、椭圆形、矩形、多边形和文字
目录 1.绘制直线line() 2.绘制圆形circle() 3.绘制椭圆形ellipse() 4.绘制矩形rectangle() 5.绘制多边形 fillPoly() 6.绘制文字putText() 7.例子 1.绘制直线line() CV_EXPORTS_W void line(InputOutputArray img,Point pt1, Point pt2,const Scalar& color,int t…...
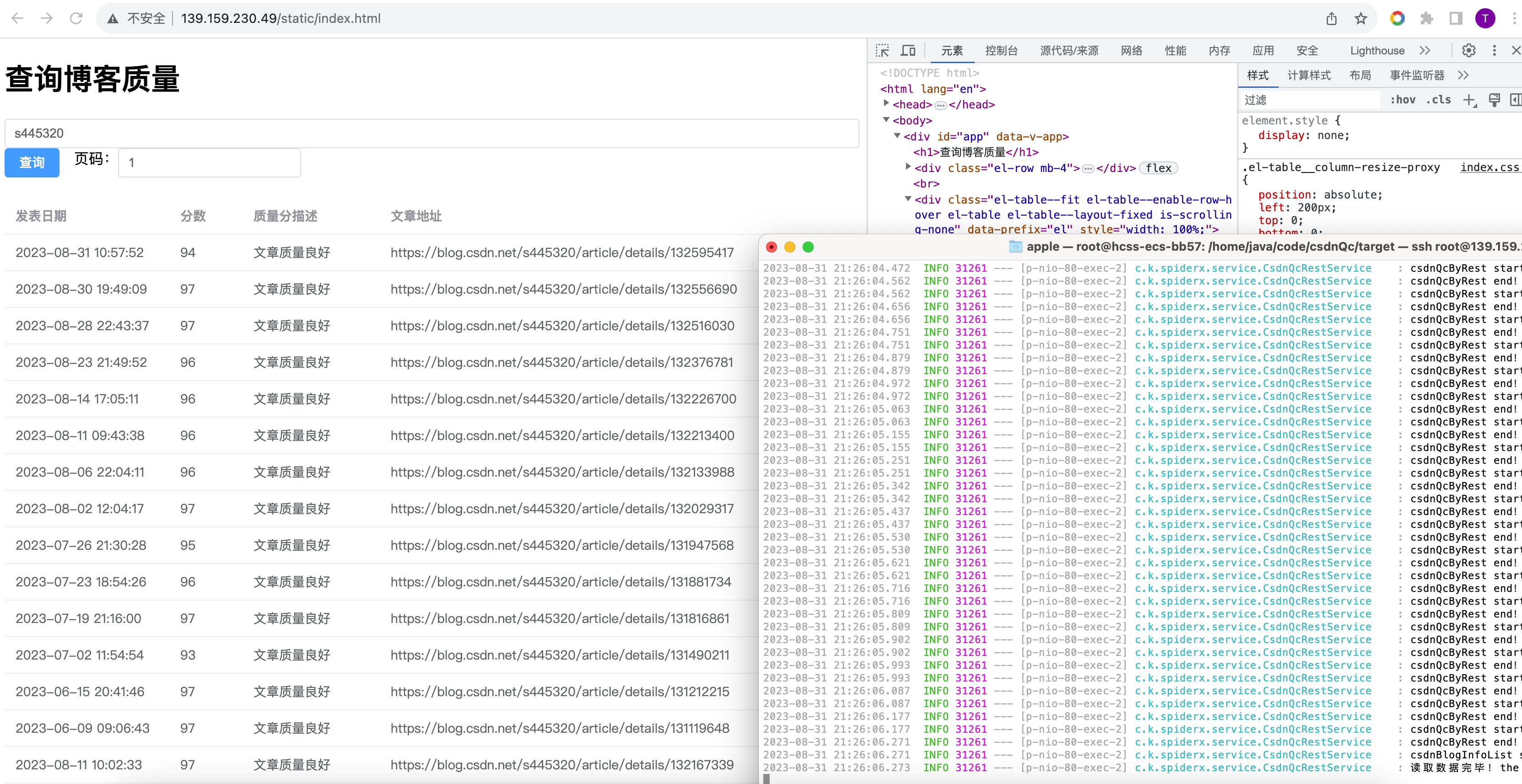
[华为云云服务器评测] Unbutnu添加SSH Key、编译启动Springboot项目
系列文章目录 第一章 [linux实战] 华为云耀云服务器L实例 Java、node环境配置 第二章 [linux实战] Unbutnu添加SSH Key、启动Springboot项目 文章目录 系列文章目录前言一、任务拆解二、配置git,添加SSH Key2.1、登录远程主机2.2、配置git用户名和邮箱2.3、生成SSH key2.4、查…...
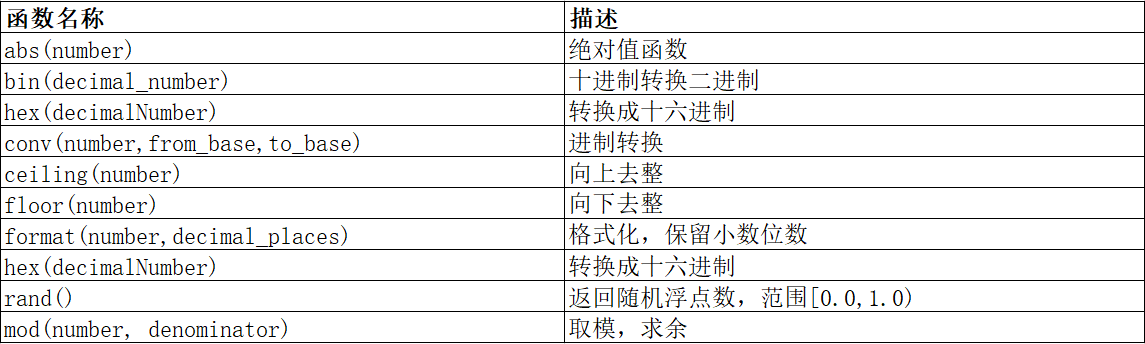
【MySQL学习笔记】(七)内置函数
内置函数 日期函数示例案例-1案例-2 字符串函数示例 数学函数其他函数 日期函数 示例 获得当前年月日 mysql> select current_date(); ---------------- | current_date() | ---------------- | 2023-09-03 | ---------------- 1 row in set (0.00 sec)获得当前时分秒…...

《Python魔法大冒险》004第一个魔法程序
在图书馆的一个安静的角落,魔法师和小鱼坐在一张巨大的桌子前。桌子上摆放着那台神秘的笔记本电脑。 魔法师: 小鱼,你已经学会了如何安装魔法解释器和代码编辑器。是时候开始编写你的第一个Python魔法程序了! 小鱼:(兴奋地两眼放光)我准备好了! 魔法师: 不用担心,…...

架构,平台,框架的区别和联系
1、解释说明 - 架构:在软件开发中,架构是指软件的整体设计和组织方式。它包括了软件的结构、组件和交互方式等方面的设计。架构定义了系统的高级结构和组织方式,以及各个组件之间的关系和交互方式。一个良好的架构可以提高软件的可维护性、可…...
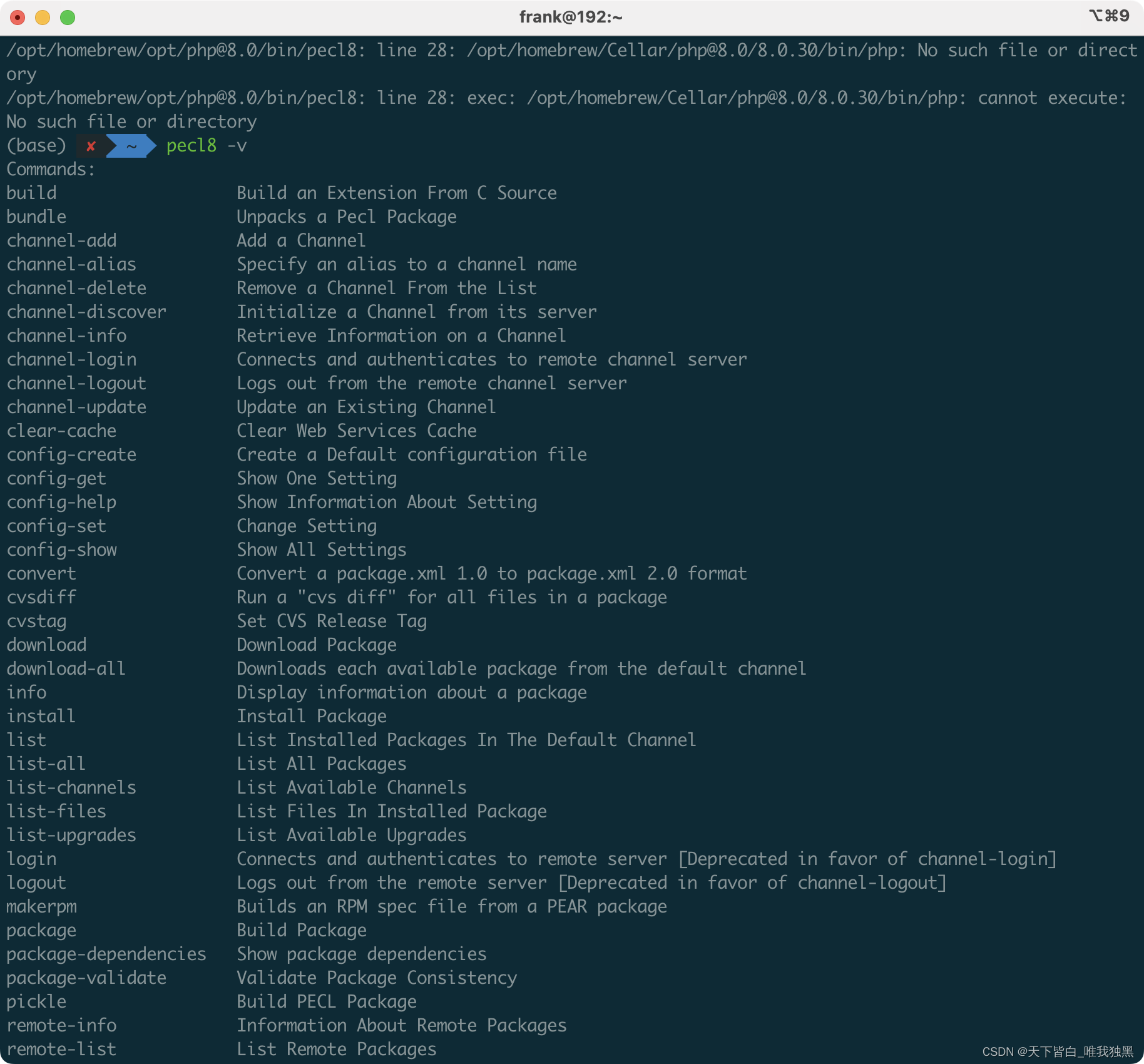
Mac 安装php多版本,brew安装php8.0
因为需要我要在mac上装两个php版本,先前我已经装过php7.4,下面我们逐步安装php8.0 开始安装8.0: 直接运行安装 brew install php8.0 遇到问题怀疑是仓库太老了,更新一下homebrew ,重新安装 brew update 安装成功了,不过看了下版本好像不能正…...
【100天精通Python】Day53:Python 数据分析_NumPy数据操作和分析进阶
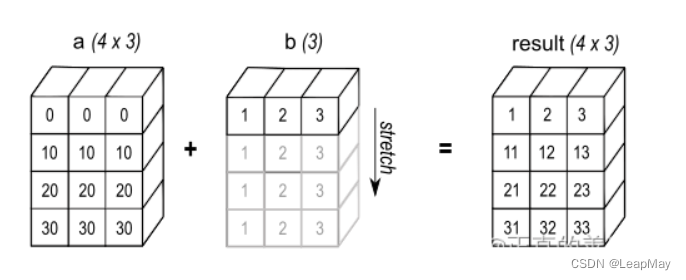
目录 1. 广播 2 文件输入和输出 3 随机数生成 4 线性代数操作 5 进阶操作 6 数据分析示例 1. 广播 广播是NumPy中的一种机制,用于在不同形状的数组之间执行元素级操作,使它们具有兼容的形状。广播允许你在不显式复制数据的情况下,对不同…...

druid连接不上doris有哪些可能原因
如果你在使用Druid连接池连接Doris时遇到问题,无法连接上数据库,可能有以下几个原因和解决方案: 网络配置问题:确保你的应用程序能够与Doris数据库所在的服务器进行通信。检查防火墙设置、网络配置以及Doris数据库的监听端口是否…...

双边滤波 Bilateral Filtering
本文是对图像去噪领域经典的双边滤波法的一个简要介绍与总结,论文链接如下: https://users.soe.ucsc.edu/~manduchi/Papers/ICCV98.pdf 1.前言引入 对一副原始灰度图像,我们将它建模为一张二维矩阵u,每个元素称为一个像素pixel&am…...
PXE批量装机
目录 前言 一、交互式 (一)、搭建环境 (二)、配置dhcp服务 (三)、FTP服务 (四)、配置TFTP服务 (五)、准备pxelinx.0文件、引导文件、内核文件 &#…...
Linux--VMware的安装和Centos
一、VMware和Linux的关系 二、VMware的安装 VM_ware桌面虚拟机 最新中文版 软件下载 (weizhen66.cn) VMware-Workstation-Lite-16.2.2-19200509-精简安装注册版.7z - 蓝奏云 如果安装不成功,则设置BIOS 三、在VMware中加入Centos 下载地址: CentOS-…...
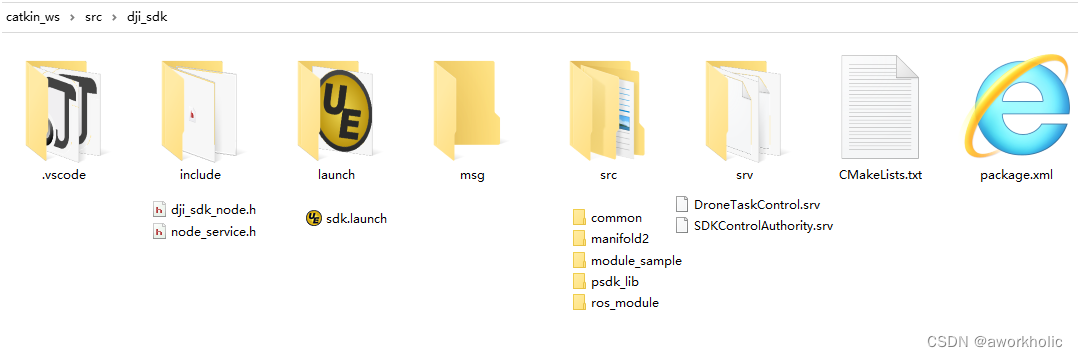
dji uav建图导航系列()ROS中创建dji_sdk节点包(一)项目结构
文章目录 1、整体项目结构1.1、 目录launch1.2、文件CMakeLists.txt1.3、文件package.xml1.4、目录include1.4、目录srv在ROS框架下创建一个无人机的节点dji_sdk,实现必需的订阅(控制指令)、发布(无人机里程计)、服务(无人机起飞降落、控制权得很)功能,就能实现一个类似…...
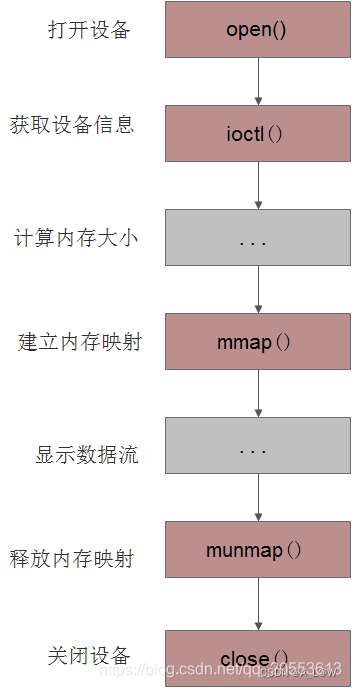
基于x86_64 ubuntu22.04的framebuffer编程
文章目录 前言一、framebuffer简介二、framebuffer接口1.framebuffer设备描述信息2.framebuffer访问接口3.查询/设置可更改信息 三、使用步骤 前言 前段时间由于笔记本没有保管好,LCD显示屏压碎了。于是,将笔记本电脑拆开查看LCD型号。在淘宝上下单买了…...

解密回文--栈
“ xyzyx ”是一个回文字符串,所谓回文字符 串就是指正读反读均相同的字符序列,如“席主席”、“记书记”、“ aha ”和“ ahaha ”均是回 文,但“ ahah ”不是回文。通过栈这个数据结构我们将很容易判断一个字符串是否为回文。 首先我们需…...

Mysql主从服务安装配置
1.下载地址 MySQL :: Download MySQL Community Server (Archived Versions)https://downloads.mysql.com/archives/community/ 2.安装配置 1.下载解压后,拷贝一份作为slave的安装目录 3.配置my.ini 由于下载mysql8版本,解压后,没有相关的my…...

双向BFS
1034 Number Game 分数 35 作者 陈越 单位 浙江大学 A number game is to start from a given number A, and to reach the destination number B by a sequence of operations. For the current number X, there are 3 types of operations: XX1 XX−1 XXN Your job is to f…...
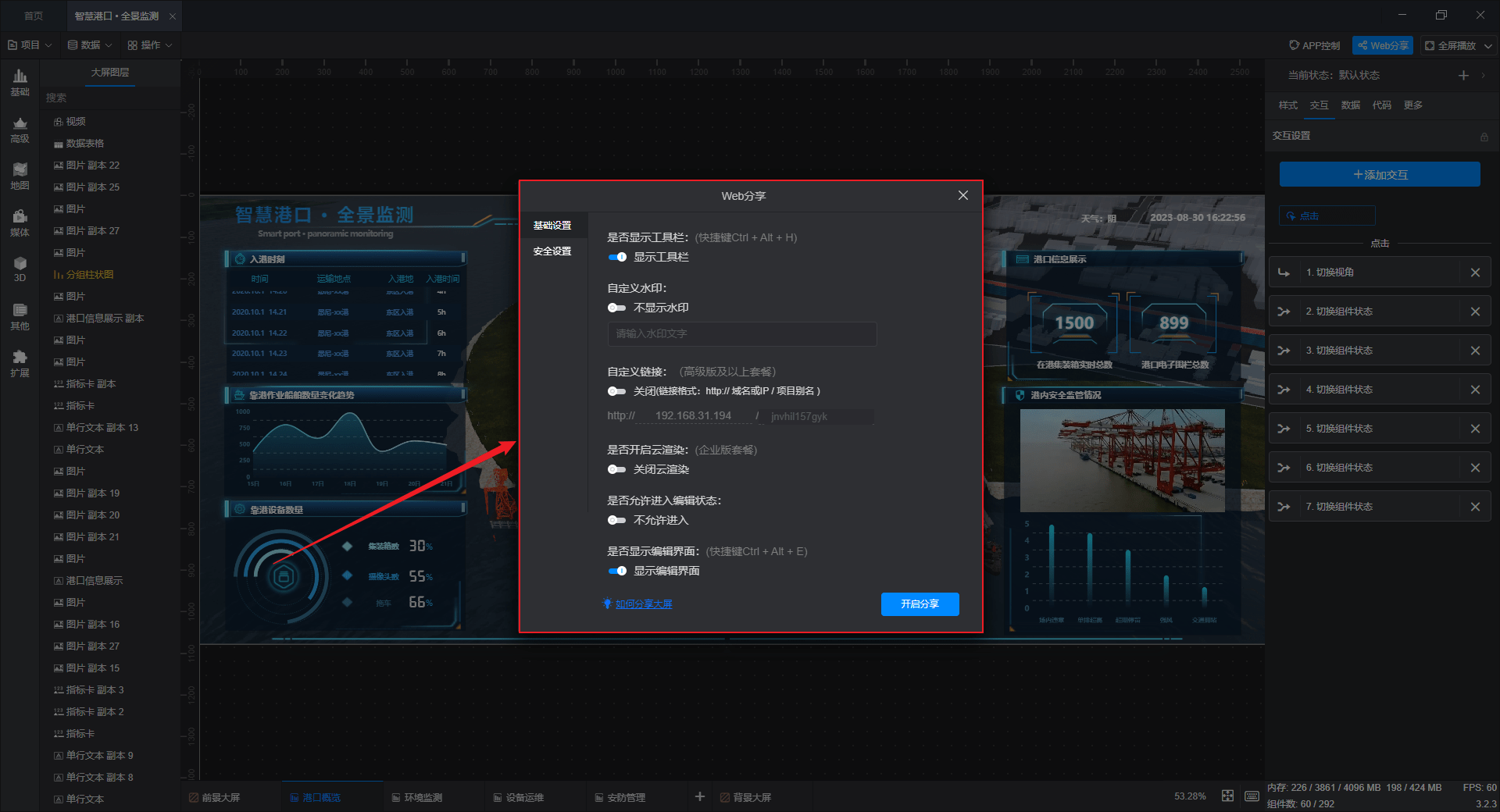
数据艺术:精通数据可视化的关键步骤
数据可视化是将复杂数据转化为易于理解的图表和图形的过程,帮助我们发现趋势、关联和模式。同时数据可视化也是数字孪生的基础,本文小编带大家用最简单的话语为大家讲解怎么制作一个数据可视化大屏,接下来跟随小编的思路走起来~ 1.数据收集和…...

MySQL 是如何实现事务的四大特性的?
分析&回答 如果你不知道事务更不知道四大特性请先看看:说说什么是事务 原子性 语句要么都执行,要么都不执行,是事务最核心的特性,事务本身来说就是以原子性来定义的,实现主要是基于undo log undo logÿ…...
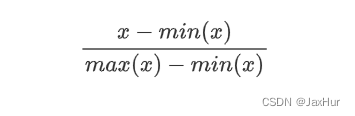
python实现zscore归一化和minmax标准化
zscore归一化: minmax from sklearn import preprocessing from sklearn.preprocessing import StandardScaler import numpy as np# 数据 x np.array([[1.,-1.,2.],[2.,0.,0.],[0.,1.,-1.]]) print(----------------minmaxscaler标准化-------------) # 调用minma…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...
