双向BFS
1034 Number Game
分数 35
作者 陈越
单位 浙江大学
A number game is to start from a given number A, and to reach the destination number B by a sequence of operations.
For the current number X, there are 3 types of operations:
X=X+1
X=X−1
X=X×N
Your job is to find the minimum number of steps required to reach B from A.
Input Specification:
Each input file contains several test cases. The first line gives a positive integer K (≤10) which is the total number of cases. For each case, three integers are given: A, B and N, where −10
5
≤A,B≤10
5
and 1<N<10. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print in a line the minimum number of steps required to reach B from
创建两个队列和两个哈希表
queue<string> que1;
queue<string> que2;
unordered_map da<string,int> da1;
unordered_map db <string,int> db2;
(25)分 双向bfs
还能怎么优化呢? 请赐教
#include <bits/stdc++.h>
using namespace std;
const int K = 20;
int k;int extend(queue<int>& que,int N,map<int,int>& set_1,map<int,int>& set_2,bool temp,int d){int len = que.size();int ans = 0xffffffff;while(len--){int top = que.front();que.pop();if(set_1.find(top+1) == set_1.end()){set_1[top+1] = d;que.push(top+1);if(set_2.find(top+1) != set_2.end()){ans = max(d + set_2[top+1],ans);}}if(set_1.find(top-1) == set_1.end()){set_1[top-1] = d;que.push(top-1);if(set_2.find(top-1) != set_2.end()){ans = max(d+set_2[top-1],ans);}}if(temp == true){if(set_1.find(top*N) == set_1.end()){set_1[top*N] = d;que.push(top*N);if(set_2.find(top*N) != set_2.end()){ans = min(set_2[top*N] + d,ans);}}}else{if(N != 0 && top % N == 0){if(set_1.find(top/N) == set_1.end()){set_1[top/N] = d;que.push(top/N);if(set_2.find(top/N) != set_2.end()){ans = min(set_2[top/N]+d,ans);}}}}}return ans;
}
int bfs(int s,int e,int n){queue<int> que1;queue<int> que2;map<int,int> set1;map<int,int> set2;que1.push(s);set1[s] = 0;que2.push(e);set2[e] = 0;if(s == e){return 0;}int d1 = 0;int d2 = 0;while(que1.size() && que2.size()){if(que1.size() < que2.size()){d1++;int t = extend(que1,n,set1,set2,true,d1);if(t != 0xffffffff){//cout<<d1<<" "<<d2<<endl;return t;}}else{d2++;int t = extend(que2,n,set2,set1,false,d2);if(t != 0xffffffff){// cout<<d1<<" "<<d2<<endl;return t;}}}return -1;
}
int main(){cin>>k;while(k--){int s,e,n;cin>>s>>e>>n;int a = bfs(s,e,n);cout<<a<<endl;}
}
相关文章:

双向BFS
1034 Number Game 分数 35 作者 陈越 单位 浙江大学 A number game is to start from a given number A, and to reach the destination number B by a sequence of operations. For the current number X, there are 3 types of operations: XX1 XX−1 XXN Your job is to f…...
数据艺术:精通数据可视化的关键步骤
数据可视化是将复杂数据转化为易于理解的图表和图形的过程,帮助我们发现趋势、关联和模式。同时数据可视化也是数字孪生的基础,本文小编带大家用最简单的话语为大家讲解怎么制作一个数据可视化大屏,接下来跟随小编的思路走起来~ 1.数据收集和…...

MySQL 是如何实现事务的四大特性的?
分析&回答 如果你不知道事务更不知道四大特性请先看看:说说什么是事务 原子性 语句要么都执行,要么都不执行,是事务最核心的特性,事务本身来说就是以原子性来定义的,实现主要是基于undo log undo logÿ…...
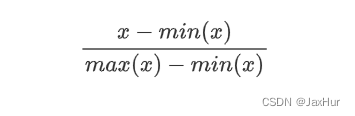
python实现zscore归一化和minmax标准化
zscore归一化: minmax from sklearn import preprocessing from sklearn.preprocessing import StandardScaler import numpy as np# 数据 x np.array([[1.,-1.,2.],[2.,0.,0.],[0.,1.,-1.]]) print(----------------minmaxscaler标准化-------------) # 调用minma…...

架构师成长之路Redis第三篇|Redis key过期清除策略
Eviction policies maxmemory 100mb 当我们设置的内存达到指定的内存量时,清除策略的配置方式决定了默认行为。Redis可以为可能导致使用更多内存的命令返回错误,也可以在每次添加新数据时清除一些旧数据以返回到指定的限制。 当达到最大内存限制时,Redis所遵循的确切行为是…...
C++智能指针之weak_ptr(保姆级教学)
目录 C智能指针之weak_ptr 概述 作用 本文涉及的所有程序 使用说明 weak_ptr的常规操作 lock(); use_count(); expired(); reset(); shared_ptr & weak_ptr 尺寸 智能指针结构框架 常见使用问题 shared_ptr多次引用同一数据,会导致两次释放同一内…...
ElementUI浅尝辄止18:Avatar 头像
用图标、图片或者字符的形式展示用户或事物信息。 常用于管理系统或web网站的用户头像,在用户账户模块更换头像操作也能看到关于Avatar组件的应用。 1.如何使用? 通过 shape 和 size 设置头像的形状和大小。 <template><el-row class"de…...
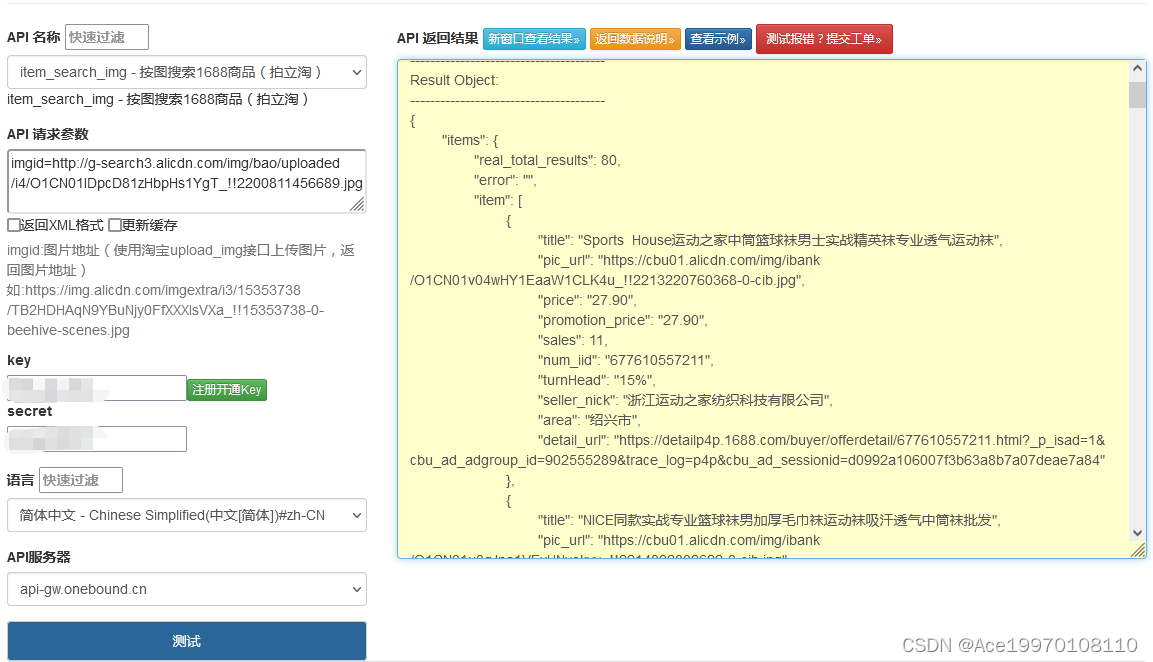
1688API技术解析,实现按图搜索1688商品(拍立淘)
一种可能的解决方案是使用图像识别和相似度匹配的算法。您可以通过将输入的图片与1688上的商品图片进行比对,找出最相似的商品。这涉及到图像特征提取、相似度计算以及数据库匹配等技术。您可以使用开源的图像处理库(如OpenCV)来进行图像处理…...

【面试经典150题】买卖股票的最佳时机
题目链接 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交易中获取的…...
selenium可以编写自动化测试脚本吗?
Selenium可以用于编写自动化测试脚本,它提供了许多工具和API,可以与浏览器交互,模拟用户操作,检查网页的各个方面。下面是一些步骤,可以帮助你编写Selenium自动化测试脚本。 1、安装Selenium库和浏览器驱动程序 首先…...

CXL.mem M2S Message 释义
🔥点击查看精选 CXL 系列文章🔥 🔥点击进入【芯片设计验证】社区,查看更多精彩内容🔥 📢 声明: 🥭 作者主页:【MangoPapa的CSDN主页】。⚠️ 本文首发于CSDN,…...
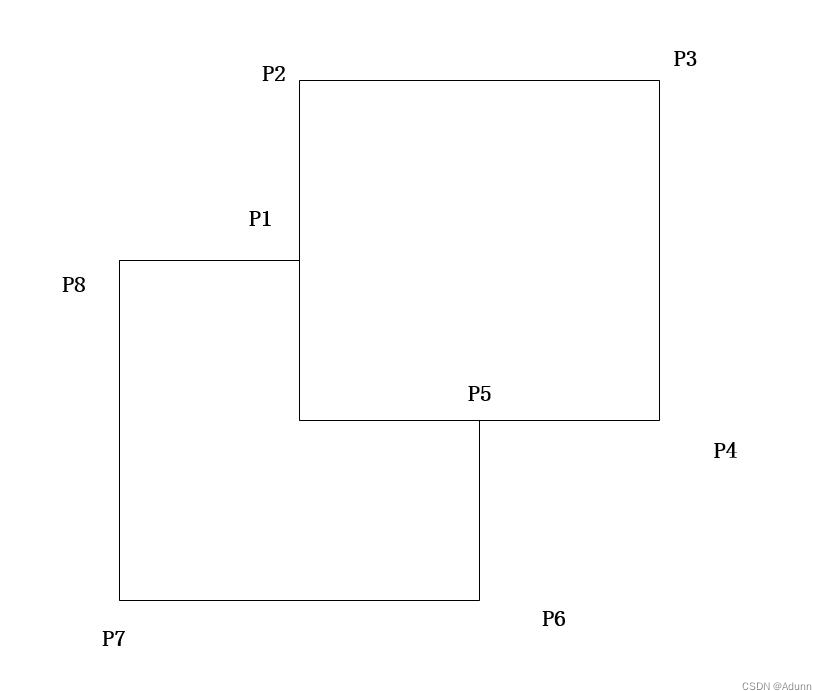
使用boost::geometry::union_ 合并边界(内、外):方案二
使用boost::geometry::union_ 合并边界(内、外):方案二 typedef boost::geometry::model::d2::point_xy<double> boost_point; typedef boost::geometry::model::polygon<boost_point> boost_Polygon;struct Point {float x;floa…...
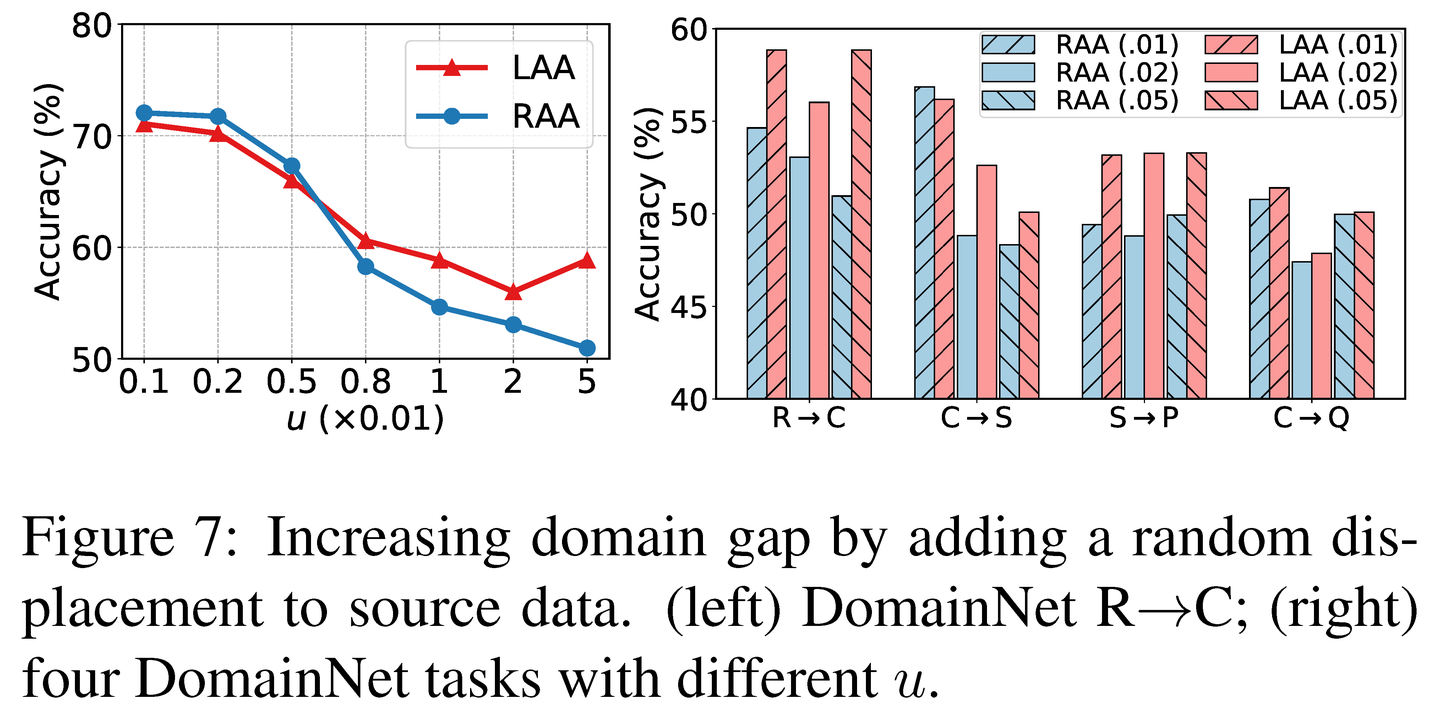
ICCV 2023 | 小鹏汽车纽约石溪:局部上下文感知主动域自适应LADA
摘要 主动域自适应(ADA)通过查询少量选定的目标域样本的标签,以帮助模型从源域迁移到目标域。查询数据的局部上下文信息非常重要,特别是在域间差异较大的情况下,然而现有的ADA方法尚未充分探索这一点。在本文中&#…...

stable diffusion实践操作-黑白稿线稿上色
系列文章目录 本文专门开一节【黑白稿线稿上色】写相关的内容,在看之前,可以同步关注: stable diffusion实践操作 文章目录 系列文章目录前言一、操作步骤1. 找到黑白线稿图 总结 前言 本章主要介绍黑白稿线稿上色,这是通过Cont…...

Python学习教程:集合操作的详细教程
前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 Python中有两种可以遍历的容器类型: 序列类型:包含字符串、列表、元祖 序列类型是线性表,就像数组一样,是在内存中开辟一块连续空间,连续存储的, 那么查找…...

球球的排列
题目传送门 引 计数DP,好像特别经典,有两种做法,我只会 O ( n 3 ) O(n^3) O(n3),有 O ( n 2 ) O(n^2) O(n2)的 解法 首先, 若 x y p 2 且 x z q 2 , 则 y z ( p q x ) 2 若xyp^2且xzq^2,则yz(\frac{pq}{x} )^2 若xyp2且xzq2,则yz(xpq…...
1783_CMD启动MATLAB同时执行一个脚本
全部学习汇总: GitHub - GreyZhang/g_matlab: MATLAB once used to be my daily tool. After many years when I go back and read my old learning notes I felt maybe I still need it in the future. So, start this repo to keep some of my old learning notes…...

C语言中内存分配的几种方式
目录 C语言中内存分配的几种方式静态内存分配栈内存分配堆内存分配内存映射文件 C语言中内存分配的几种方式 静态内存分配 静态内存分配是在程序编译时分配内存,通常用于全局变量和静态变量。这些变量的内存空间在程序的整个运行期间都是存在的。 栈内存分配 栈内存…...
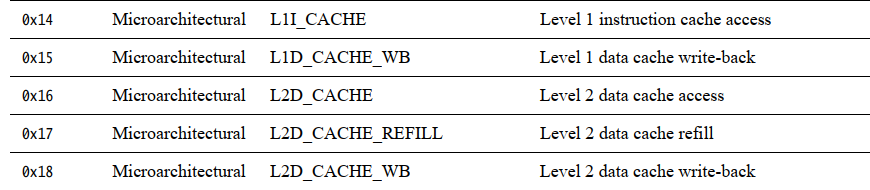
组相联cache如何快速实现cache line eviction并使用PMU events验证
如何快速实现cache line eviction 一,什么是cache hit、miss、linefill、evict ?1.1 如果要程序员分别制造出cache hit、miss、linefill、evict这四种场景,该怎么做? 二,实现cache line eviction的方法1.1 直接填充法3…...
【Stable Diffusion安装】支持python3.11 window版
前言 主要的安装步骤是参考B站播放量第一的视频,但是那位阿婆主应该是没有编程经验,只强调使用3.10,而python最新版本是3.11。 理论上来说,只是一个小版本的不同,应该是可以安装成功了。自己摸索了下,挺费…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
