代码随想录训练营第41天|343.整数拆分,96.不同的二叉搜索树
代码随想录训练营第41天|343.整数拆分,96.不同的二叉搜索树
- 343.整数拆分
- 文章
- 思路
- 代码
- 96.不同的二叉搜索树
- 文章
- 思路
- 代码
- 总结
343.整数拆分
文章
代码随想录|0343.整数拆分
思路
二刷不难
d p [ i ] = M a x j ( m a x ( j + 1 , d p [ j ] ) ∗ ( i − j ) ) \begin{equation} dp[i]=Max_j(max(j + 1, dp[j]) * (i - j)) \end{equation} dp[i]=Maxj(max(j+1,dp[j])∗(i−j))
代码
class Solution {public int integerBreak(int n) {int[] dp = new int[n];int i, j;int prefix;for (i = 1; i < n; ++i) {for (j = 0; j < i; ++j) {dp[i] = Math.max(dp[i], Math.max(j + 1, dp[j]) * (i - j));}}// for (i = 0; i < n; ++i) {// System.out.print(" " + dp[i]);// }return dp[n - 1];}
}
96.不同的二叉搜索树
文章
代码随想录|0096.不同的二叉搜索树
思路
二刷不难
二叉搜索树的数量等于左子树的数量乘右子树的数量
其组合有(0, n - 1), … (n - 1, 0)共n种
d p [ i ] = ∑ j < i d p [ j ] ∗ d p [ i − 1 − j ] dp[i] = \sum_{j<i} dp[j]*dp[i - 1 - j] dp[i]=j<i∑dp[j]∗dp[i−1−j]
代码
class Solution {public int numTrees(int n) {int[] dp = new int[n + 1];int i, j;dp[0] = 1;for (i = 1; i < n + 1; ++i) {for (j = 0; j < i; ++j) {dp[i] += dp[j] * dp[i - 1 - j];}}return dp[n];}
}
总结
二刷就乏善可陈
相关文章:

代码随想录训练营第41天|343.整数拆分,96.不同的二叉搜索树
代码随想录训练营第41天|343.整数拆分,96.不同的二叉搜索树 343.整数拆分文章思路代码 96.不同的二叉搜索树文章思路代码 总结 343.整数拆分 文章 代码随想录|0343.整数拆分 思路 二刷不难 d p [ i ] M a x j ( m a x ( j 1 , d p [ j ] ) ∗ ( i − j ) ) \…...

高防服务器与云防产品都适用哪些情况
高防服务器与云防护产品(如高防IP,高防CDN)都可以对DDOS、CC等攻击进行防护,在现如今的互联网市场上,不法分子经常会通过DDOS、CC等攻击服务器,干扰业务正常运行,以此来获得利益。 高防服务器是…...

【广州华锐互动】AR远程连接专家进行协同管理,解放双手让协同更便捷
AR远程协同系统是一种基于AR技术,实现远程设备维修和技术支持的系统。该系统通过将虚拟信息叠加在现实世界中,实现对设备的全方位监控和管理,并可以通过AR眼镜等终端设备,实时查看设备的各项数据和信息,为设备维修提供…...

PNG图片压缩原理
png??png的图片我们每天都在用,可是png到底是什么,它的压缩原理是什么? 很好,接下来我将会给大家一一阐述。 什么是PNG PNG的全称叫便携式网络图型(Portable Network Graphics)是…...

[ Linux Audio 篇 ] Linux Audio 子系统资料集锦
Linux Audio 子系统资料 背景OSS VS ALSAALSA 驱动ALSA libALSA Plugin音频延迟音频调试音频书籍 背景 最近需要准备Linux Audio 相关的PPT,于是将以往的知识点和遇到的问题进行整理和梳理,以便向大家讲解。同时,还整理了在这个过程中发现的…...

VR全景对行业发展有什么帮助?VR全景制作需要注意什么?
引言: 虚拟现实(Virtual Reality,简称VR)早已不再是科幻电影的概念,而是在以惊人的速度改变着我们的世界。VR全景,作为其中的重要组成部分,正为多个行业带来了全新的机遇。 一、VR全景的应用领…...

Unity网络请求队列
引子 最近的一个项目中由于某个需求,需要多次请求后台接口数据,就自己封装了一下网络请求的队列;刚刚好给大家分享一下,互相交流学习 简述 Unity 的网络请求队列是由 UnityWebRequestQueue 类实现的。这个类继承自 MonoBehaviou…...

【Spring Boot】使用XML配置文件实现数据库操作(一)
使用XML配置文件实现数据库操作(一) 1.SQL映射文件 SQL映射文件就是我们通常说的mapper.xml配置文件,主要实现SQL语句的配置和映射,同时实现Java的POJO对象与数据库中的表和字段进行映射关联的功能。 1.1 mapper.xml的结构 下…...

PMP中常用英文术语
常用术语(五) Project 项目 为完成一个唯一的产品或服务的一种一次性努力。 Project Charter 项目许可证 由高级管理部门提供的一个文档,它给项目经理特权把组织的资源应用到项目工作中。 Project Communication Management 项目沟通管理 项目…...

【Apollo学习笔记】——规划模块TASK之SPEED_BOUNDS_PRIORI_DECIDERSPEED_BOUNDS_FINAL_DECIDER
文章目录 前言SPEED_BOUNDS_PRIORI_DECIDER功能简介SPEED_BOUNDS_FINAL_DECIDER功能简介SPEED_BOUNDS_PRIORI_DECIDER相关配置SPEED_BOUNDS_FINAL_DECIDER相关配置SPEED_BOUNDS_DECIDER流程将障碍物映射到ST图中ComputeSTBoundary(PathDecision* path_decision)ComputeSTBounda…...

score_inverse_problems运行环境,pycharm重新安装,jax,jaxlib的GPU版本安装-230831
尝试运行https://github.com/yang-song/score_inverse_problems pycharm2019不支持python3.10,其实后来我用来3.8…… pycharm2022.3.3的安装,涉及激活(淘宝5元),搜狗拼音输入(shift不能切换输入法&#x…...

VSC++: 奇怪的风吹
void 奇怪的风吹() {//缘由https://ask.csdn.net/questions/1062454int aa[]{15, 30, 12, 36, 11, 20, 19, 17, 16, 18, 38, 15, 30, 12, 36, 11, 20, 19, 17, 16, 18, 38, -1},j 0, a 0, y 0, z 0;while (aa[j] > 0){if (j && aa[j] > 35 || aa[j] < 15)…...

被动操作系统指纹识别的强大功能可实现准确的物联网设备识别
到 2030 年,企业网络和互联网上的物联网设备数量预计将达到290 亿。这种指数级增长无意中增加了攻击面。 每个互连设备都可能为网络攻击和安全漏洞创造新的途径。Mirai 僵尸网络通过使用数千个易受攻击的 IoT 设备对关键互联网基础设施和热门网站发起大规模 DDoS 攻…...
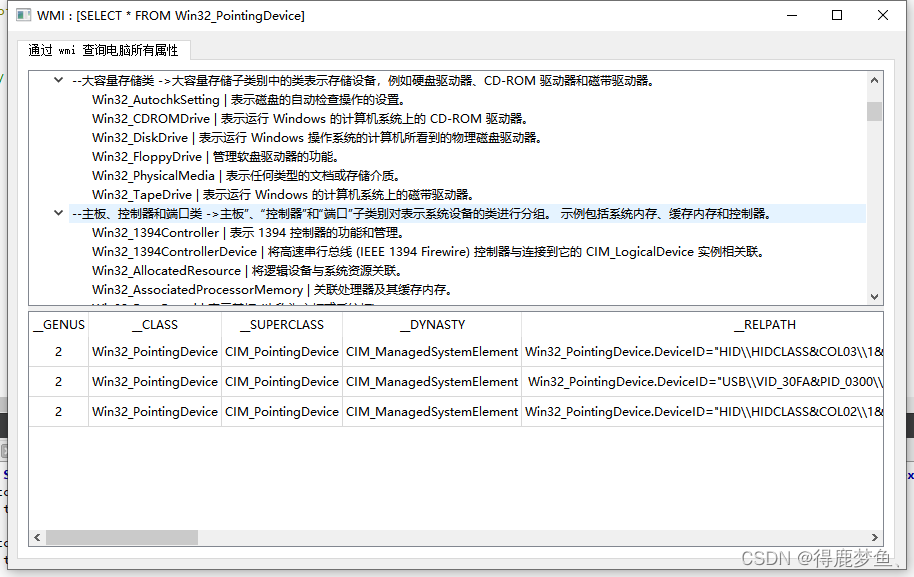
QT/C++获取电脑系统,主板型号,CPU型号,硬盘型号,内存大小等相关信息(二)通过Windows Server (WMI)查询
Qt/C调用windows Api库通过wmi的方式查询电脑能获取更多详细信息,也更加合理有技术性。 建议使用MSCV编译器,如MSCV 2017 ,Qt版本 : 5.13.1 目录导读 关于 WMI示例:创建 WMI 应用程序示例:打印Wmi执行的查询项的所有属性头文件引用…...
自建音乐服务器Navidrome之一
这里写自定义目录标题 1.1 官方网站 2. Navidrome 简介2.1 简介2.2 特性 3. 准备工作4. 视频教程5. 界面演示5.1 初始化页5.2 专辑页 前言 之前给大家介绍过 Koel 音频流服务,就是为了解决大家的这个问题:下载下来的音乐,只能在本机欣赏&…...

ACL 访问控制 过滤数据 维护网络安全(第七课)
一 ACL 简介 ACL是Access Control List(访问控制列表)的缩写,是一种用于控制文件、目录、网络设备等资源访问权限的方法。ACL可以对每个用户或用户组设置不同的访问权,即在访问控制清单中为每个用户或用户组指定允许或禁止访问该资源的权限。它通常由一系列规则组成,规则…...

3D视觉测量:面对面的对称度 点对(附源码)
文章目录 0. 测试效果1. 基本内容2. 3D视觉测量对称度测量思路3. 代码实现4. 参考文章目录:3D视觉测量目录微信:dhlddxB站: Non-Stop_目标:通过3D视觉方法计算面对面的对称度0. 测试效果 数据说明:此测试点云是通过UG建模,Meshlab降采样得到,数据比较理想,仅作为测试使用…...

无涯教程-JavaScript - RANK函数
RANK函数取代了Excel 2010中的RANK.EQ函数。 描述 该函数返回数字列表中数字的等级。数字的等级是其相对于列表中其他值的大小。 如果对列表进行排序,则数字的排名将是其位置。 语法 RANK (number,ref,[order])争论 Argument描述Required/OptionalNumberThe number whose…...
蓝牙发展现状
目录 一、产品分类1、Bluetooth经典2、Bluetooth低能耗(LE)3、二者差异 二、出货量三、未来需要加强的方向四、技术行业细分五、学习资料1、蓝牙官网2、大神博客——于忠军 一、产品分类 1、Bluetooth经典 Bluetooth Classic无线电,也被称为Bluetooth 基本速率/增强…...
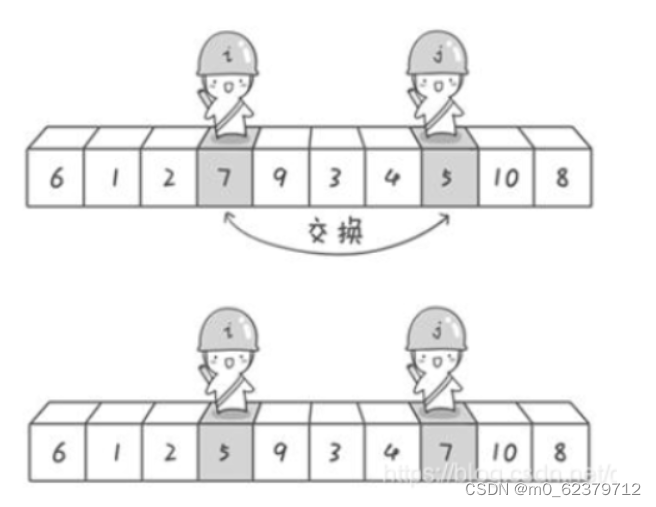
排序算法问题
给你一个整数数组 nums,请你将该数组升序排列。 示例 1: 输入:nums [5,2,3,1] 输出:[1,2,3,5] 示例 2: 输入:nums [5,1,1,2,0,0] 输出:[0,0,1,1,2,5] 代码如下: 1.插入排序(简…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
