第 361 场 LeetCode 周赛题解
A 统计对称整数的数目
枚举 x x x
class Solution {
public:int countSymmetricIntegers(int low, int high) {int res = 0;for (int i = low; i <= high; i++) {string s = to_string(i);if (s.size() & 1)continue;int s1 = 0, s2 = 0;for (int k = 0; k < s.size(); k++)if (k < s.size() / 2)s1 += s[k] - '0';elses2 += s[k] - '0';if (s1 == s2)res++;}return res;}
};
B 生成特殊数字的最少操作
双指针:则若字符串操作完后为 0 0 0 ,设字符串长为 n n n ,则需要 n n n 或 n − 1 n-1 n−1 (字符串中含
0)操作使得字符串变为 0 0 0 , 若字符串操作完后至少有两位数字,则其最后两位只能是 { 25 , 50 , 75 , 00 } \{25, 50, 75, 00\} {25,50,75,00} 其中之一,枚举可能的后两位,用双指针计算要得到当前枚举值的最少操作数
class Solution {
public:int minimumOperations(string num) {vector<string> tar{"25", "50", "75", "00"};int n = num.size();int res = num.find('0') == num.npos ? n : n - 1;for (auto &s: tar) {int i = s.size() - 1;int j = n - 1;int cur = 0;//得到当前枚举值的最少操作数for (; i >= 0 && j >= 0;) {if (s[i] == num[j]) {i--;j--;} else {j--;cur++;}}if (i < 0)res = min(res, cur);}return res;}
};
C 统计趣味子数组的数目


前缀和:设数组 l i li li 有: l i i = { 1 , n u m s [ i ] % m o d = k 0 , n u m s [ i ] % m o d ≠ k li_i=\left\{\begin{matrix} 1 & , nums[i]\%mod=k \\ 0 & , nums[i]\%mod\ne k \end{matrix}\right. lii={10,nums[i]%mod=k,nums[i]%mod=k,设 l i li li 上的前缀和为 p s i = ( ∑ j = 0 j < i l i i ) % m o d ps_i=(\sum_{j=0}^{j<i} li_i)\%mod psi=(∑j=0j<ilii)%mod ,设子数组 n u m s [ l , r ] nums[l,r] nums[l,r] 为趣味子数组,则有: ( p s r + 1 − p s l ) % m o d = k (ps_{r+1}-ps_{l})\%mod=k (psr+1−psl)%mod=k,即有 p s l = ( ( p s r + 1 − k ) % m o d + m o d ) % m o d ps_l=((ps_{r+1}-k)\%mod+mod)\%mod psl=((psr+1−k)%mod+mod)%mod。
class Solution {
public:using ll = long long;long long countInterestingSubarrays(vector<int> &nums, int modulo, int k) {unordered_map<int, ll> cnt;//cnt[val]: 前缀和val出现的次数cnt[0] = 1;//前缀为空int s = 0;//当前前缀和ll res = 0;for (int i = 0; i < nums.size(); i++) {if (nums[i] % modulo == k)s = (s + 1) % modulo;int s_l = ((s - k) % modulo + modulo) % modulo;res += cnt[s_l];cnt[s]++;}return res;}
};
D 边权重均等查询
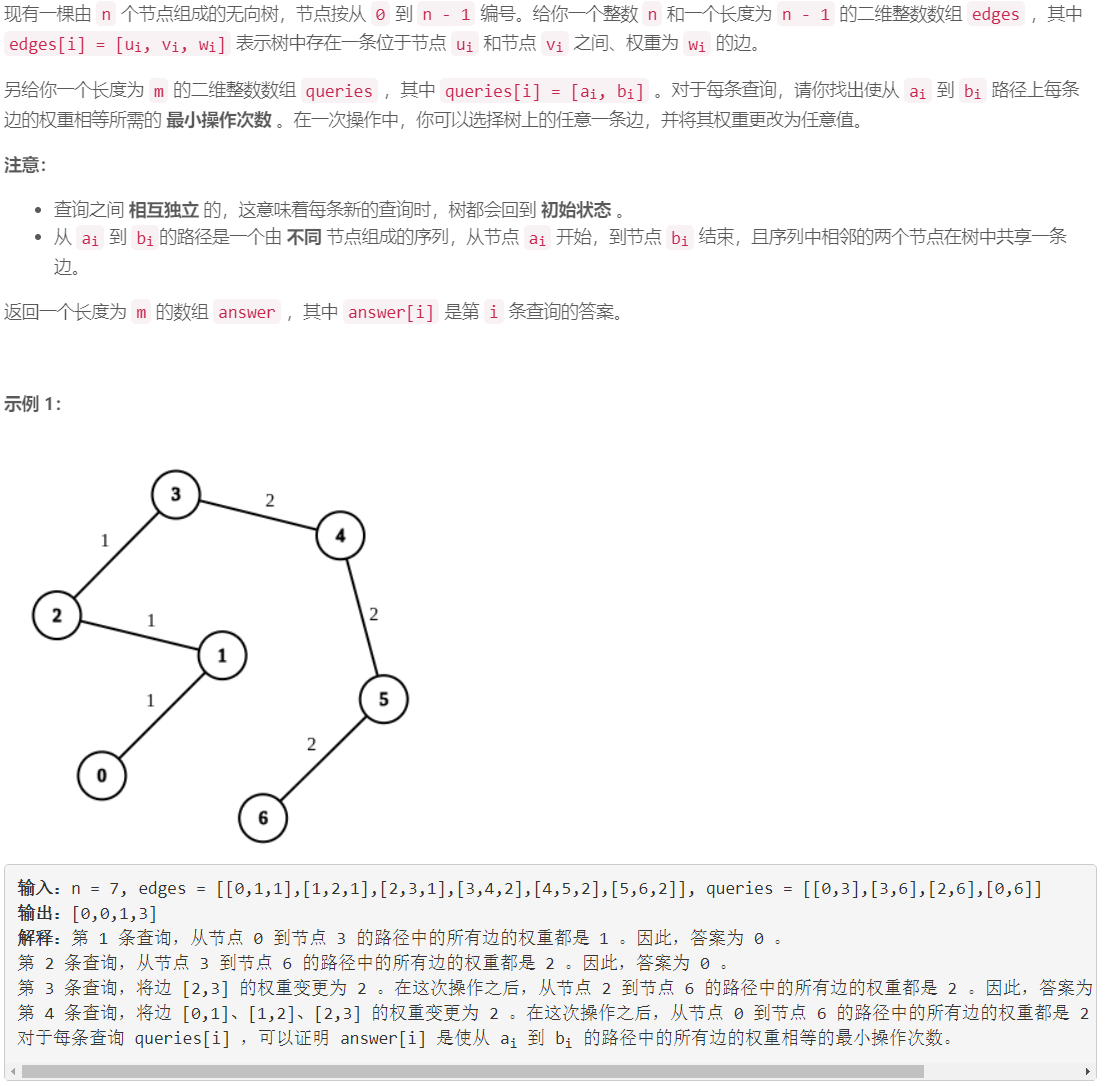
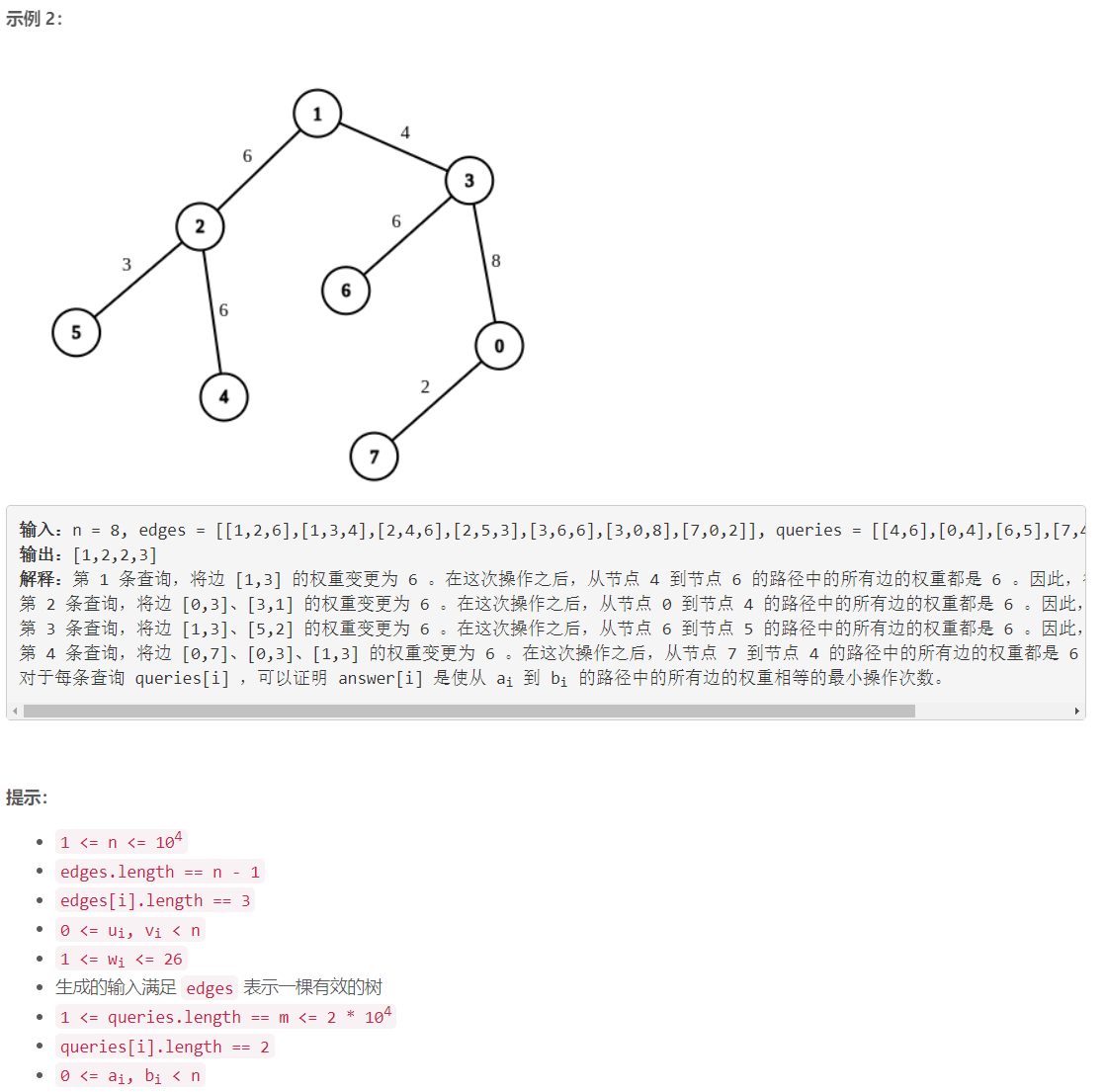
倍增+枚举:1)预处理:设 0 0 0 为树的根节点,枚举边的权重 w _ i d w\_id w_id,从树根开始 d f s dfs dfs ,计算各节点 u u u 到树根的路径上的边数 l e v e l [ u ] level[u] level[u],以及节点 u u u 到树根的路径上边权重为 w _ i d w\_id w_id 的边的数目 s [ u ] [ w _ i d ] s[u][w\_id] s[u][w_id],求倍增数组 p p p: p [ u ] [ j ] p[u][j] p[u][j]为与 u u u 距离为 2 j 2^j 2j的祖先节点。2)对一个查询 ( a , b ) (a,b) (a,b),用倍增的方式求 a a a 和 b b b 的最近公共祖先 c c c ,然后枚举 w _ i d w\_id w_id ,将 a a a 和 b b b 间路径上的边的边权统一为 w _ i d w\_id w_id 的操作数为: ( l e v e l [ a ] − l e v e l [ c ] − ( s [ a ] [ w _ i d ] − s [ c ] [ w _ i d ] ) ) + ( l e v e l [ b ] − l e v e l [ c ] − ( s [ b ] [ w _ i d ] − s [ c ] [ w _ i d ] ) ) \left ( level[a] - level[c] - (s[a][w\_id] - s[c][w\_id]) \right ) + \left ( level[b] - level[c] - (s[b][w\_id] - s[c][w\_id]) \right ) (level[a]−level[c]−(s[a][w_id]−s[c][w_id]))+(level[b]−level[c]−(s[b][w_id]−s[c][w_id]))
class Solution {
public:vector<int> minOperationsQueries(int n, vector<vector<int>> &edges, vector<vector<int>> &queries) {vector<pair<int, int>> e[n];//邻接表int mx_w = 0, mn_w = INT32_MAX;//最大权重、最小权重for (auto &ei: edges) {e[ei[0]].emplace_back(ei[1], ei[2]);e[ei[1]].emplace_back(ei[0], ei[2]);mx_w = max(mx_w, ei[2]);mn_w = min(mn_w, ei[2]);}int level[n], s[n][27];int p[n][15];function<void(int, int, int, int, int)> dfs = [&](int cur, int par, int lev, int sum, int w_id) {if (w_id == mn_w)//倍增数组一轮dfs即可计算for (int i = 0; i < 15; i++)p[cur][i] = i != 0 ? p[p[cur][i - 1]][i - 1] : par;level[cur] = lev;s[cur][w_id] = sum;for (auto &[j, w]: e[cur])if (j != par)dfs(j, cur, lev + 1, w == w_id ? sum + 1 : sum, w_id);};for (int i = mn_w; i <= mx_w; i++)//枚举w_iddfs(0, 0, 0, 0, i);vector<int> res;res.reserve(queries.size());for (auto &qi: queries) {int a = qi[0], b = qi[1];if (a == b) {res.push_back(0);continue;}if (level[a] < level[b])swap(a, b);int c = a;//c最终为a和b的最近公共祖先for (int step = level[a] - level[b], ind = 0; step >= (1 << ind); ind++)if (step >> ind & 1)c = p[c][ind];if (c != b) {int b_ = b;for (int ind = 14; ind >= 0; ind--) {if (p[c][ind] != p[b_][ind]) {c = p[c][ind];b_ = p[b_][ind];}}c = p[c][0];}int res_i = INT32_MAX;for (int w_id = mn_w; w_id <= mx_w; w_id++) {//枚举w_idint t1 = level[a] - level[c] - (s[a][w_id] - s[c][w_id]);int t2 = level[b] - level[c] - (s[b][w_id] - s[c][w_id]);res_i = min(res_i, t1 + t2);}res.push_back(res_i);}return res;}
};
相关文章:

第 361 场 LeetCode 周赛题解
A 统计对称整数的数目 枚举 x x x class Solution { public:int countSymmetricIntegers(int low, int high) {int res 0;for (int i low; i < high; i) {string s to_string(i);if (s.size() & 1)continue;int s1 0, s2 0;for (int k 0; k < s.size(); k)if …...

07-架构2023版-centos+docker部署Canal 实现多端数据同步
canal 工作原理 canal 模拟 MySQL slave 的交互协议,伪装自己为 MySQL slave ,向 MySQL master 发送dump 协议MySQL master 收到 dump 请求,开始推送 binary log 给 slave (即 canal )canal 解析 binary log 对象(原始为 byte 流)基于日志增量订阅和消费的业务包括 数据库镜…...
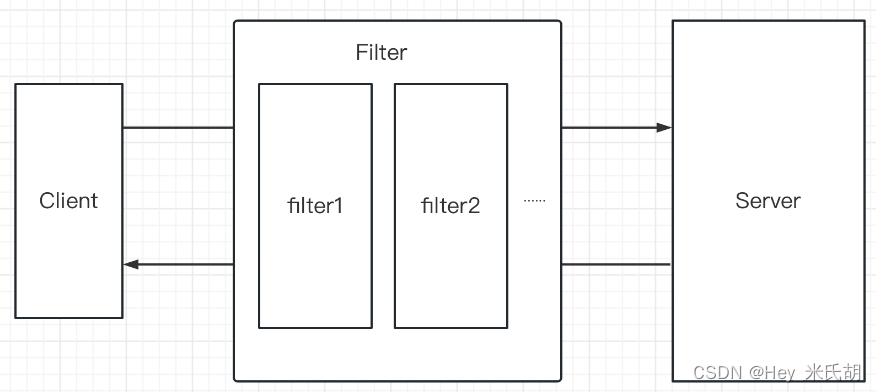
过滤器的应用-Filter
过滤器 1.工作原理 2.创建Filter 2.1通过注解的方式实现 //创建一个类,实现Filter接口 WebFilter(urlPatterns "/myfilter") //urlPatterns表示需要拦截的路径 public class MyFilter implements Filter {Overridepublic void doFilter(ServletReques…...

leetcode236. 二叉树的最近公共祖先(java)
二叉树的最近公共祖先 题目描述递归法代码演示 上期经典 题目描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q …...

spacy安装旧版本en_core_web_sm的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
Qt +VTK+Cmake 编译和环境配置(第一篇 采坑)
VTK下载地址:https://vtk.org/download/ cmake下载地址:https://cmake.org/download/ 版本对应方面,如果你的项目对版本没有要求,就不用在意。我就是自己随机搭建的,VTK选择最新版本吧,如果后面其他的库不…...

2023开学礼《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书南宁师范大学图书馆
2023开学礼《乡村振兴战略下传统村落文化旅游设计》许少辉八一新书南宁师范大学图书馆...

C++/C# : C#和C++的不同
C#和C是两种不同的编程语言,虽然在某些方面它们具有相似之处,但它们也有一些明显的不同点,如下: C是一种静态类型编程语言,而C#是一种动态类型编程语言。 C允许开发者手动管理内存的分配和释放,但是C#的垃…...

PCL-直通滤波器原理及实验
文章目录 原理使用过程代码实验总结 原理 直通滤波器的作用是过滤在指定维度方向上取值不在给定值域内的点,即点云数据有xyz三维坐标,选择一个方向的维度的数据,设置一个范围,在这个范围中的点云会被保留,不在此范围内…...
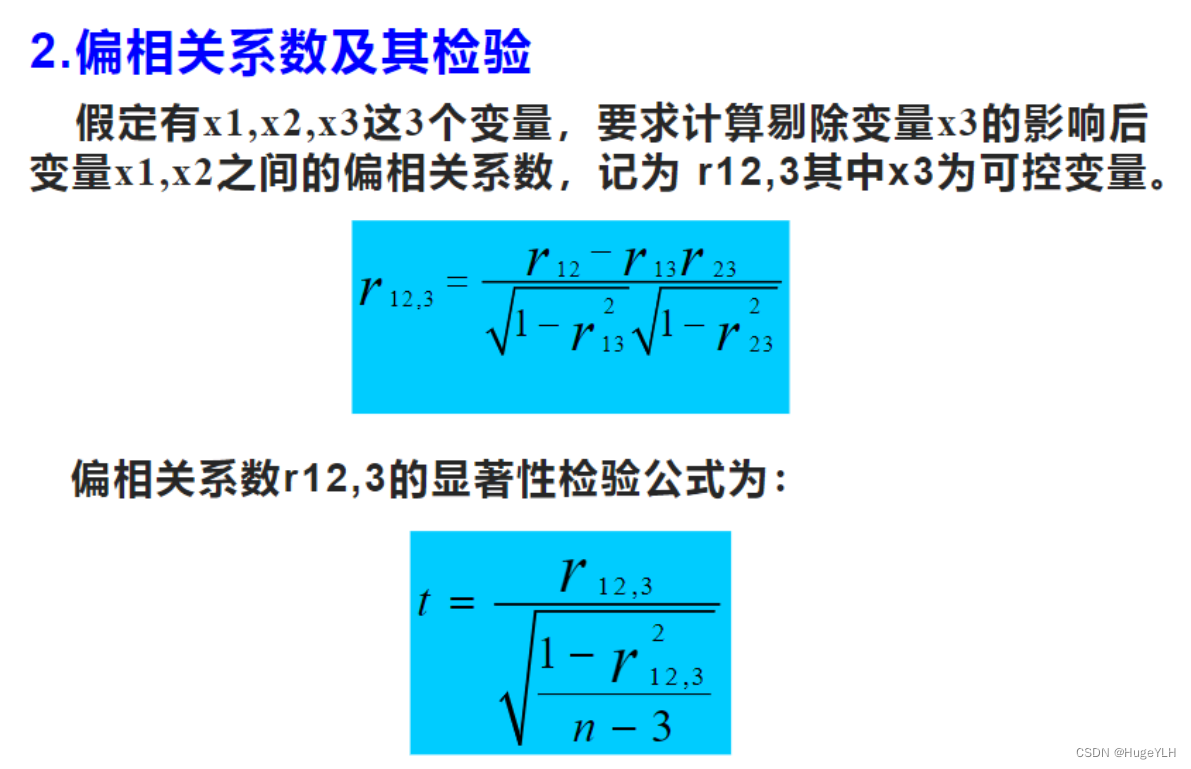
数学建模:相关性分析
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:相关性分析 文章目录 数学建模:相关性分析相关性分析两变量的相关分析PearsonSpearmanKendall tua-b 双变量关系强度测量的指标相关系数的性质代码实现example偏相关分析 相…...
thinkPHP项目搭建
1 宝塔添加站点 (1)打开命令提示行,输入以下命令,找到hosts文件。 for /f %P in (dir %windir%\WinSxS\hosts /b /s) do copy %P %windir%\System32\drivers\etc & echo %P & Notepad %P (2)添加域…...

C++中几种处理函数返回值的方式
目录 C中几种处理函数返回值的方式:值返回引用返回指针返回总结 C中几种处理函数返回值的方式: 值返回 函数可以返回一个具体的值,例如整数、浮点数、结构体、类对象等。返回值被复制到函数调用点,在调用点可以直接使用或赋给其…...

跟我学c++中级篇——c++中的Abominable Function Types
一、Abominable Function Types Abominable Function Types,令人讨厌(憎恶)的函数类型。这个在c的技术点中,很少有人了解。那么什么是Abominable Function Types呢?看下面的例子: using func void(); using func…...
计算机毕设之基于python+django+mysql的影片数据爬取与数据分析(包含源码+文档+部署教程)
影片数据爬取与数据分析分为两个部分,即管理员和用户。该系统是根据用户的实际需求开发的,贴近生活。从管理员处获得的指定账号和密码可用于进入系统和使用相关的系统应用程序。管理员拥有最大的权限,其次是用户。管理员一般负责整个系统的运…...

slog正式版来了:Go日志记录新选择!
在大约一年前,我就写下了《slog:Go官方版结构化日志包[1]》一文,文中介绍了Go团队正在设计并计划在下一个Go版本中落地的Go官方结构化日志包:slog[2]。但slog并未如预期在Go 1.20版本[3]中落地,而是在golang.org/x/exp…...
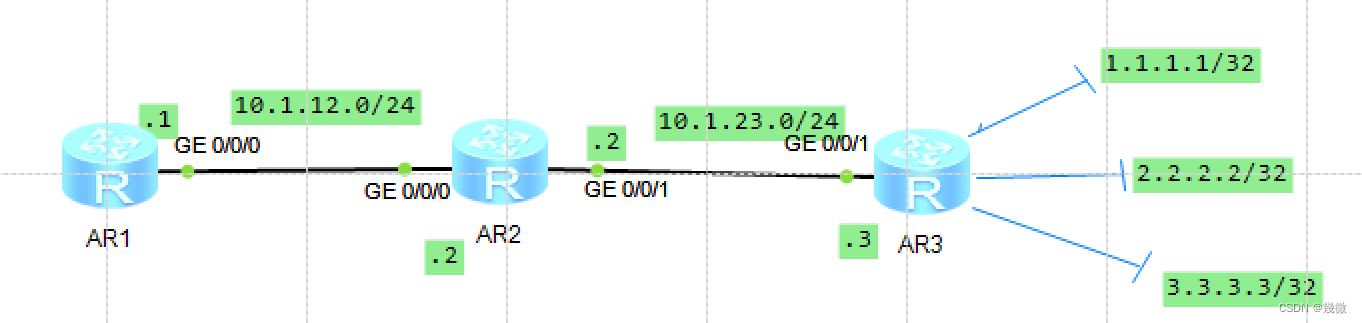
华为静态路由配置实验(超详细讲解+详细命令行)
系列文章目录 华为数通学习(7) 前言 一,静态路由配置 二,网络地址配置 AR1的配置: AR2的配置: AR3的配置: 三,测试是否连通 AR1的配置: 讲解: AR2的配置&#…...

axios源码学习
1 判断一个对象是否普通对象 Symbol.toStringTag:可以修改Object.prototype.toString.call返回的后缀,普通对象自带该属性,不需要设置,如果设置说明该对象不是普通对象Symbol.iterator:拥有该属性的对象可以使用for o…...

【SpingBoot】详细介绍SpringBoot项目中前端请求到数据库再返回前端的完整数据流转,并用代码实现
在SpringBoot项目中,前端请求到最终返回的完整数据流转一般包括以下几个步骤: 前端发送HTTP请求到后端Controller。 Controller接收到请求后,调用相关Service处理业务逻辑。 Service调用DAO层获取数据。 DAO层访问数据库获取数据。 数据库…...

kubesphere devops使用
一、创建项目 1 创建项目 企业管理员切换到相应企业空间(租户),创建项目,k8s集群会创建一个相同名字的namespace。如下图所示管理员创建一个ipaas-devops项目。 2.创建镜像拉取密钥信息 进入项目如ipaas-devops,选择配置->保密字典->创建…...

Selenium如何用于编写自动化测试脚本?
Selenium如何用于编写自动化测试脚本?它提供了许多测试工具和API,可以与浏览器交互,模拟用户操作,检查网页的各个方面。下面是一些步骤,可以帮助你编写Selenium自动化测试脚本。 1、安装Selenium库和浏览器驱动程序 首…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
