学习高级数据结构:探索平衡树与图的高级算法
文章目录
- 1. 平衡树:维护数据的平衡与高效性
- 1.1 AVL 树:严格的平衡
- 1.2 红黑树:近似平衡
- 2. 图的高级算法:建模复杂关系与优化
- 2.1 最小生成树:寻找最优连接方式
- 2.2 拓扑排序:解决依赖关系
- 拓展思考

🎉欢迎来到数据结构学习专栏~学习高级数据结构:探索平衡树与图的高级算法
- ☆* o(≧▽≦)o *☆嗨~我是IT·陈寒🍹
- ✨博客主页:IT·陈寒的博客
- 🎈该系列文章专栏:数据结构学习
- 📜其他专栏:Java学习路线 Java面试技巧 Java实战项目 AIGC人工智能 数据结构学习
- 🍹文章作者技术和水平有限,如果文中出现错误,希望大家能指正🙏
- 📜 欢迎大家关注! ❤️
在计算机科学领域,数据结构是构建算法和程序的基础。在初级阶段,我们已经掌握了一些基本的数据结构,如数组、链表、栈和队列等。然而,在实际应用中,涉及到大规模数据处理、高效搜索以及复杂关系建模等场景,我们需要更高级的数据结构来满足这些需求。在这篇文章中,我们将深入学习两个重要的高级数据结构:平衡树和图的高级算法。

1. 平衡树:维护数据的平衡与高效性
平衡树是一种特殊的二叉搜索树,它在每次插入或删除操作后能够自动调整,以保持树的平衡状态。这种平衡性质使得树的高度保持在对数级别,从而保证了查找、插入和删除操作的时间复杂度都在 O(log n) 级别。

1.1 AVL 树:严格的平衡
AVL 树是一种最早提出的平衡二叉搜索树,它要求任何节点的左子树和右子树的高度差(平衡因子)不超过 1。当插入或删除节点后破坏了平衡性,AVL 树会通过旋转操作来重新平衡。下面是一个简单的 AVL 树示例:
class AVLNode {int key;AVLNode left;AVLNode right;int height;
}

1.2 红黑树:近似平衡
红黑树是另一种广泛使用的平衡二叉搜索树,它通过在每个节点上增加一个额外的颜色信息(红色或黑色)来保持平衡。红黑树的平衡性要求是:每个节点要么是红色,要么是黑色,根节点是黑色,红色节点的子节点都是黑色。这些规则确保了红黑树的高度不会超过 2 倍的最小高度。
class RedBlackNode {int key;RedBlackNode left;RedBlackNode right;RedBlackNode parent;int color; // 0 for black, 1 for red
}

2. 图的高级算法:建模复杂关系与优化
图是一种由节点和边构成的数据结构,用于表示对象之间的关系。图的高级算法在社交网络分析、路径搜索、网络优化等领域有着广泛的应用。
2.1 最小生成树:寻找最优连接方式
最小生成树是一个无向图的子图,它包含图中的所有节点,并且连接了这些节点,使得总边权最小。常用的算法包括 Prim 算法和 Kruskal 算法。Prim 算法从一个起始节点出发,逐步添加与当前树相连且权值最小的边;Kruskal 算法则按照边的权值从小到大逐步加入。
class Edge {int source;int destination;int weight;
}// Prim's Algorithm
List<Edge> primMST(Graph graph) {// Implementation here
}// Kruskal's Algorithm
List<Edge> kruskalMST(Graph graph) {// Implementation here
}

2.2 拓扑排序:解决依赖关系
拓扑排序用于有向无环图(DAG)中,将图的节点线性排序,使得对于每一条有向边 (u, v),节点 u 在排序中出现在节点 v 之前。拓扑排序在任务调度、编译器优化等领域有着广泛的应用。
// Kahn's Algorithm
List<Integer> topologicalSort(Graph graph) {// Implementation here
}

拓展思考
- 平衡树在数据库索引中的应用:了解 B 树、B+ 树等在数据库索引中的应用,以提高查询效率。
- 图的高级算法在社交网络分析中的作用:如何利用图算法挖掘社交网络中的信息、关系和影响力。
- 平衡树与哈希表的对比:分析在不同场景下,平衡树和哈希表的优势和劣势。

在本文中,我们深入学习了高级数据结构中的平衡树和图的高级算法。通过了解它们的原理、应用和代码示例,我们能够更好地解决实际问题,优化算法效率,构建更高效的程序。在实际开发中,根据问题的需求,选择合适的数据结构和算法是提升系统性能的重要一环。
🧸结尾
❤️ 感谢您的支持和鼓励! 😊🙏
📜您可能感兴趣的内容:
- 【Java面试技巧】Java面试八股文 - 掌握面试必备知识(目录篇)
- 【Java学习路线】2023年完整版Java学习路线图
- 【AIGC人工智能】Chat GPT是什么,初学者怎么使用Chat GPT,需要注意些什么
- 【Java实战项目】SpringBoot+SSM实战:打造高效便捷的企业级Java外卖订购系统
- 【数据结构学习】从零起步:学习数据结构的完整路径
相关文章:

学习高级数据结构:探索平衡树与图的高级算法
文章目录 1. 平衡树:维护数据的平衡与高效性1.1 AVL 树:严格的平衡1.2 红黑树:近似平衡 2. 图的高级算法:建模复杂关系与优化2.1 最小生成树:寻找最优连接方式2.2 拓扑排序:解决依赖关系 拓展思考 …...

centos7离线安装neo4j
一、准备需要的rpm包 本地环境执行如下命令: docker pull couchbase/centos7-systemd docker run -it couchbase/centos7-systemd bash # 可能需要换源 yum update -y vi /etc/yum.conf # 修改其中的keepcache1 rpm --import https://debian.neo4j.com/neotechnol…...
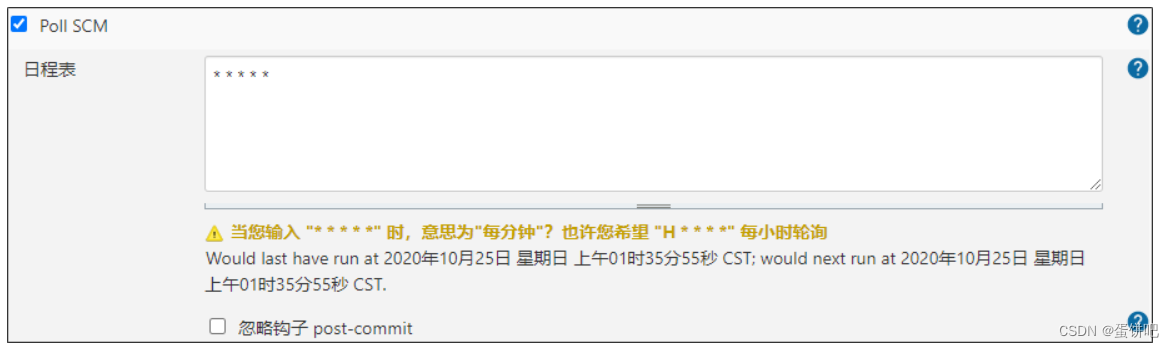
【黑马头条之项目部署_持续集成Jenkins】
本笔记内容为黑马头条项目的项目部署_持续集成部分 目录 一、内容介绍 1、什么是持续集成 2、持续集成的好处 3、今日内容 二、软件开发模式 1、软件开发生命周期 2、软件开发瀑布模型 3、软件的敏捷开发 三、Jenkins安装配置 1、Jenkins介绍 2、Jenkins环境搭建 …...
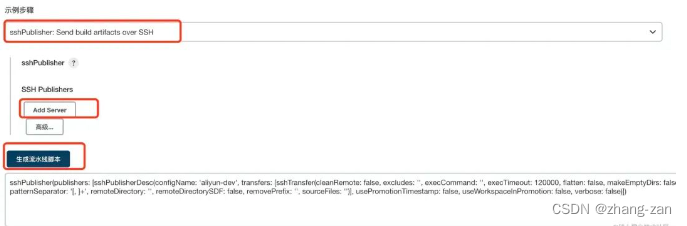
前端自动化部署,Devops,CI/CD
DevOps 提到 Jenkins,想到的第一个概念就是 CI/CD 在这之前应该再了解一个概念。 DevOps Development 和 Operations 的组合,是一种方法论,并不特指某种技术或者工具。DevOps 是一种重视 Dev 开发人员和 Ops 运维人员之间沟通、协作的流程。…...

22 元类技术(面向切片编程)|ORM的实现|抽象类与接口类
文章目录 前情知识补充hasattr 函数setattr函数getattr函数join 函数 元类技术使用type创建类什么是元类(概念总结)\_\_metaclass\_\_属性使用metaclass 的函数方式进行创建类使用metaclass 的类方式进行创建类 自定义元类 元类实现ORM接口类与抽象类抽象…...

fuchsia系统介绍
fuchsia系统 Fuchsia,是由Google公司开发的继Android和Chrome OS之后的第三个系统,已在Github中公开的部分源码可以得知。Google对于Fuchsia的说明是“Pink(粉红)Purple(紫色)Fuchsia(灯笼海棠…...

解决Jenkins执行Python脚本不能实时输出打印信息的问题
问题: 在使用Jenkins的shell command来执行python脚本时,总是会等脚本执行完毕,最后一次性才把脚本中的print语句给打印出来; 解决方法: 在print语句后加上sys.stdout.flush(), 就可以达到实时输出的目的了。...

2021年03月 C/C++(五级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:最小新整数 给定一个十进制正整数n(0 < n < 1000000000),每个数位上数字均不为0。n的位数为m。 现在从m位中删除k位(0<k < m),求生成的新整数最小为多少? 例如: n = 9128456, k = 2, 则生成的新整数最小为12456 时间…...
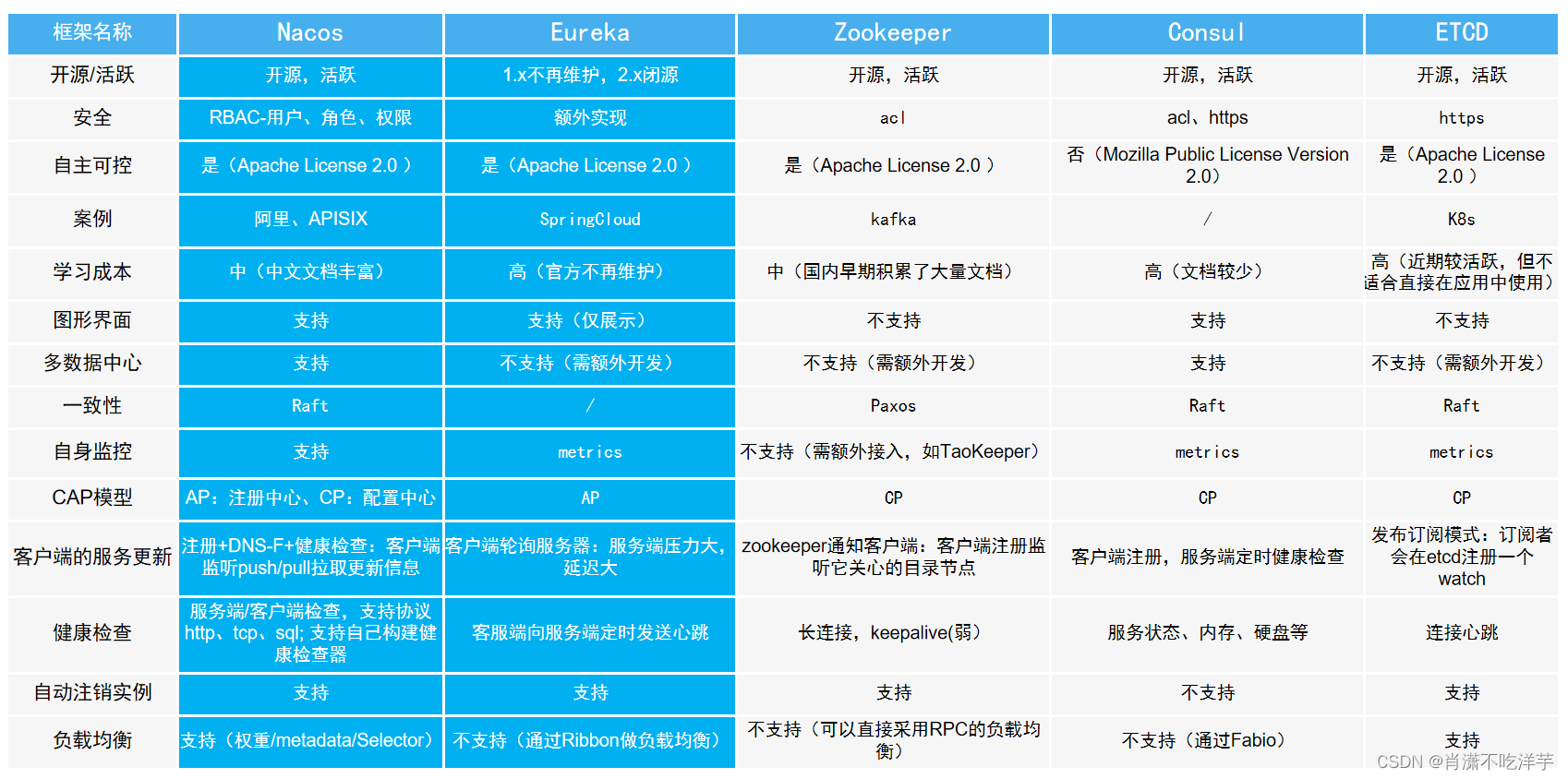
【微服务】服务发现和管理技术框架选型调研
选型背景 方案对比 结论 结合实际业务和开发需要,着重考虑性能可靠性、功能和社区支持程度三方面,认为Nacos更适合作为服务发现和管理的技术框架。具体理由如下: 性能更好,可靠性更高 经过阿里、APISIX、SpringCloudAlibaba,阿…...
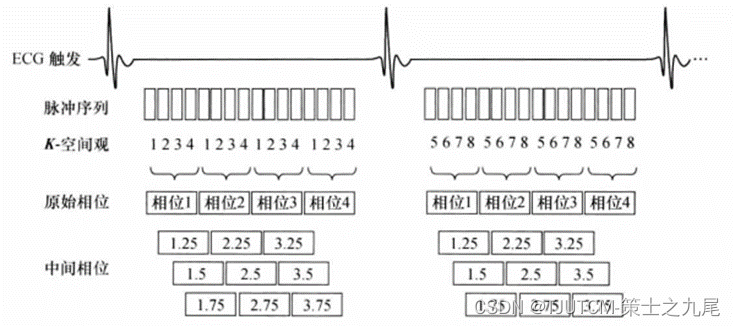
【核磁共振成像】观共享重建
目录 一、K空间关键孔技术-数据采集二、BRISK技术三、TRICKS技术四、实时成像和滑动窗重建五、心电触发电影(CINE)采集六、分段心脏采集和观共享 一、K空间关键孔技术-数据采集 对于笛卡尔K空间,一个相位编码行有时称为一个K空间观。一般情况下,每帧图像…...

〔020〕Stable Diffusion 之 骨骼姿势 篇
✨ 目录 🎈 姿势检测 / OpenPose🎈 姿势检测 OpenPose 参数介绍🎈 姿势检测 OpenPose 基本使用🎈 深度库 / Depth Lib🎈 深度库 Depth Lib 参数介绍🎈 3D姿势检测 / 3D Openpose Editor🎈 3D姿势检测 3D Openpose Editor 参数介绍🎈 3D姿势检测 3D Openpose Ed…...

使用Python进行Base64编码和解码
假设您有一个想要通过网络传输的二进制图像文件。您很惊讶对方没有正确接收该文件 - 该文件只是包含奇怪的字符! 嗯,您似乎试图以原始位和字节格式发送文件,而所使用的媒体是为流文本而设计的。 避免此类问题的解决方法是什么?答…...

MongoDB的数据恢复与备份
MongoDB的数据恢复与备份 在MongoDB中,备份和恢复数据是一项关键任务,可以确保数据的安全性并防止意外数据丢失。本文将介绍MongoDB的数据恢复与备份原理并提供相关的编程代码和配置。 1. 数据备份原理 MongoDB提供了多种备份数据…...
Java之SpringCloud Alibaba【五】【微服务 Sentinel整合openfeign进行降级】
一、Sentinel整合openfeign 1、复制一下order-openfeign项目(创建order-openfeign-sentinel) 然后在stock-nacos当中编写对应的接口 RequestMapping("/reduct2")public String reduct2(){int a 1/0;System.out.println("扣减库存"…...
电脑前置耳机没声音怎么办
有很多小伙伴反映在将自己的耳机连接到主机前面时没有声音,这是怎么回事呢,遇到这种情况应该怎么解决呢,下面小编就给大家详细介绍一下电脑前置耳机没声音的解决方法,有需要的小伙伴可以来看一看电脑前面耳机没声音。 解决方法&a…...

package.json 详解
文章目录 package.json1. name2. version3. description4. homepage5. bugs6. license7. author, contributors8. funding9. files10. main11. module12. browser13. bin14. man15. directories15.1 directories.bin15.2 directories.man 16. repository17. scripts18. config1…...

springboot配置ym管理各种日记(log)
1:yml配置mybatis_plus默认日记框架 mybatis-plus:#这个作用是扫描xml文件生效可以和mapper接口文件使用,#如果不加这个,就无法使用xml里面的sql语句#启动类加了MapperScan是扫描指定包下mapper接口生效,如果不用MapperScan可以在每一个mapp…...

你知道Vue 3.0中Treeshaking特性吗?
介绍 Vue 3.0引入了Tree-shaking特性,旨在优化构建过程并减小最终生成的代码大小。Tree-shaking是一种在构建时移除未使用代码的技术,通过分析模块的依赖关系,将没有被引用的部分从最终的打包文件中排除掉。这可以大大减少应用的体积&#x…...
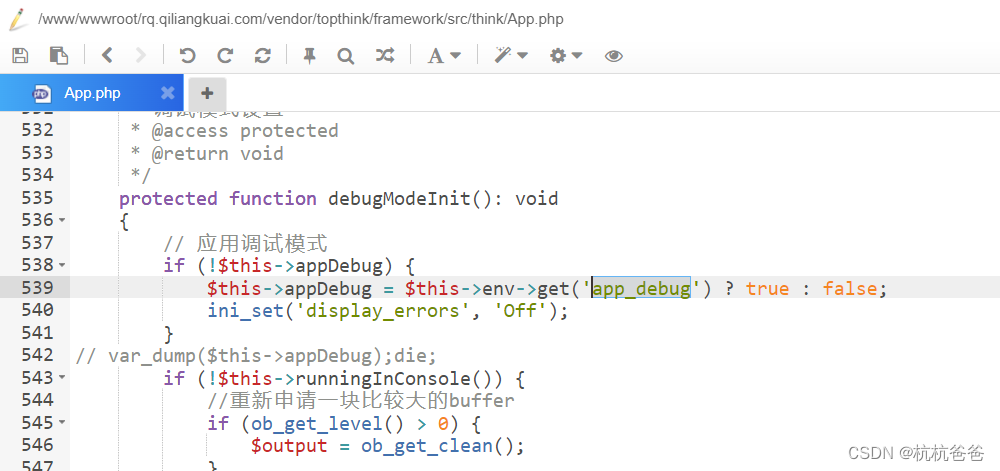
TP6 开启关闭debug
config 不起作用,还得来这里改: 或者单个方法里加: $this->app->debug(true); //临时错误调试...
Linux centos7 bash编程(break和continue)
在学习shell知识时,简单编程要从格式入手。 首先学习好单行注释和多行注释。 先学习简单整数的打印输出,主要学习echo命令,学习选项-e -n的使用。 下面的练习是常用的两个分支跳转程序:break和continue。 #!/bin/bash # 这是单…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
