解决SpringBoot项目war部署到tomcat下无法Nacos中注册服务问题
问题说明
怎么解决Spring Boot项目部署到tomcat下无法Nacos中注册服务问题",希望能够解决您遇到有关问题。
在使用Nacos作为注册中心的Spring Boot项目,以war包形式部署到服务器上,启动项目发现该服务无法在Nacos中注册。
分析
查看源码,需从nacos的注册类找起,查找后发现,nacos注册类NacosAutoServiceRegistration继承了Spring Cloud中AbstractAutoServiceRegistration, 而在AbstractAutoServiceRegistration中绑定了一个监听事件,监听内置容器启动完成事件,监听到获取容器端口后向注册中心注册。
@EventListener({WebServerInitializedEvent.class})public void bind(WebServerInitializedEvent event) {ApplicationContext context = event.getApplicationContext();if (!(context instanceof ConfigurableWebServerApplicationContext) || !"management".equals(((ConfigurableWebServerApplicationContext)context).getServerNamespace())) {this.port.compareAndSet(0, event.getWebServer().getPort());this.start();}}而使用外部容器时,不能监听到事件,所以自动注册失败。
解决方案
Spring Boot提供了PostConstruct注解属性和ApplicationRunner接口并实现run方法即可前者比较简单,是在应用起好之后执行一些初始化动作。通过这个接口我们可以实现启动项目后注册服务。使用这种方法,需要在配置文件中配置端口号,如果一个应用部署很多端口,每个应用都要配置,很不方便。故可获取外部tomcat自动设置端口。经测试,方法可行。
代码如下:
@Component
@Slf4j
public class NacosRegister {@Autowiredprivate NacosRegistration registration;@Autowiredprivate NacosAutoServiceRegistration nacosAutoServiceRegistration;@Value("${server.port}")String serverPort;@PostConstructpublic void registerInstance() throws Exception {if (registration != null && serverPort != null) {String tomcatPort = serverPort;try {tomcatPort = getPort();} catch (Exception e) {log.warn("获取外部Tomcat端口异常:", e);}registration.setPort(Integer.parseInt(tomcatPort));nacosAutoServiceRegistration.start();}}/*** 获取外部tomcat端口*/public String getPort() {try {MBeanServer beanServer = ManagementFactory.getPlatformMBeanServer();Set<ObjectName> objectNames = beanServer.queryNames(new ObjectName("*:type=Connector,*"), Query.match(Query.attr("protocol"), Query.value("HTTP/1.1")));String port = objectNames.iterator().next().getKeyProperty("port");return port;} catch (Exception ex) {log.error("NacosRegister.getPort()动态获取端口异常:", ex.toString());return serverPort;}}
提示
部署项目要注意版本问题,如Spring Boot 2.0.6应该部署在tomcat8以上版本,tomcat8以下版本可能有些变化,导致项目启动报错。所以大家尽量使用tomcat8以上版本吧
相关文章:

解决SpringBoot项目war部署到tomcat下无法Nacos中注册服务问题
问题说明 怎么解决Spring Boot项目部署到tomcat下无法Nacos中注册服务问题",希望能够解决您遇到有关问题。 在使用Nacos作为注册中心的Spring Boot项目,以war包形式部署到服务器上,启动项目发现该服务无法在Nacos中注册。 分析 …...

C++中的##、#符号含义
在C中,## 和 # 是两个不同的预处理符号。这些符号都是在C的预处理阶段使用的,用于在代码编译之前对文本进行操作。 #(字符串化操作符): 用于将宏参数转换为字符串常量。 #define STRINGIZE(x) #x const char* str S…...

探究Vue3中的Composition API:优化组件逻辑的新利器
一、toRef函数 在 Vue 3.0 中,引入了一种新的响应式 API,即 toRef。toRef 函数可以将一个普通值转换为响应式引用类型,这样就可以在模板中直接使用这个响应式引用类型的属性,并且当该属性发生变化时,视图会自动更新。 <templat…...

Google Services Framework 谷歌服务框架的安装以及遇到的常见问题
安装谷歌三件套: 1、Google 服务框架(Google Services Framework)下载地址: https://www.apkmirror.com/apk/google-inc/google-services-framework/ 注意一定要选择与自己手机对应的安卓系统版本的服务框架。 2、Google Play Se…...

学习高级数据结构:探索平衡树与图的高级算法
文章目录 1. 平衡树:维护数据的平衡与高效性1.1 AVL 树:严格的平衡1.2 红黑树:近似平衡 2. 图的高级算法:建模复杂关系与优化2.1 最小生成树:寻找最优连接方式2.2 拓扑排序:解决依赖关系 拓展思考 …...

centos7离线安装neo4j
一、准备需要的rpm包 本地环境执行如下命令: docker pull couchbase/centos7-systemd docker run -it couchbase/centos7-systemd bash # 可能需要换源 yum update -y vi /etc/yum.conf # 修改其中的keepcache1 rpm --import https://debian.neo4j.com/neotechnol…...
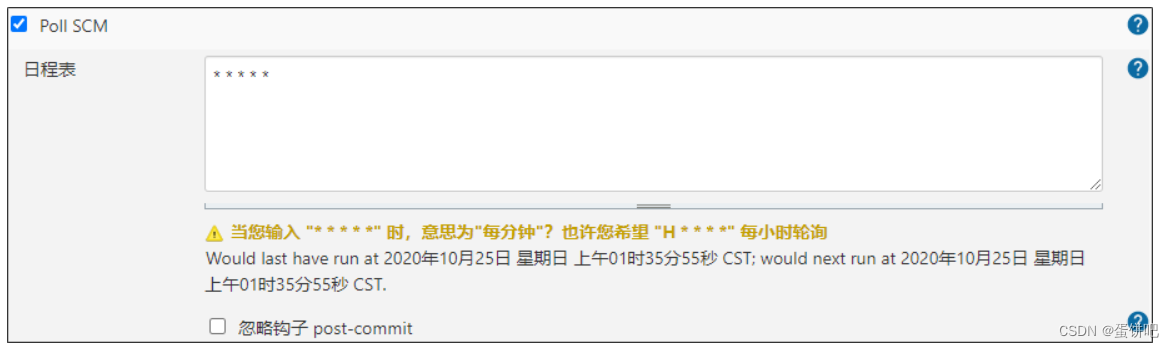
【黑马头条之项目部署_持续集成Jenkins】
本笔记内容为黑马头条项目的项目部署_持续集成部分 目录 一、内容介绍 1、什么是持续集成 2、持续集成的好处 3、今日内容 二、软件开发模式 1、软件开发生命周期 2、软件开发瀑布模型 3、软件的敏捷开发 三、Jenkins安装配置 1、Jenkins介绍 2、Jenkins环境搭建 …...
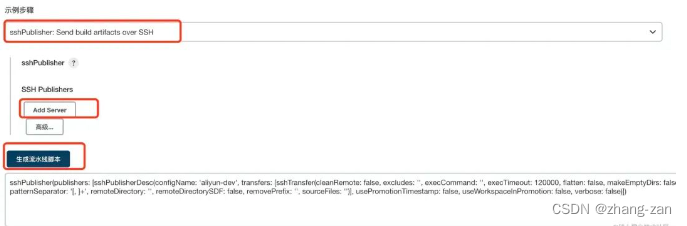
前端自动化部署,Devops,CI/CD
DevOps 提到 Jenkins,想到的第一个概念就是 CI/CD 在这之前应该再了解一个概念。 DevOps Development 和 Operations 的组合,是一种方法论,并不特指某种技术或者工具。DevOps 是一种重视 Dev 开发人员和 Ops 运维人员之间沟通、协作的流程。…...

22 元类技术(面向切片编程)|ORM的实现|抽象类与接口类
文章目录 前情知识补充hasattr 函数setattr函数getattr函数join 函数 元类技术使用type创建类什么是元类(概念总结)\_\_metaclass\_\_属性使用metaclass 的函数方式进行创建类使用metaclass 的类方式进行创建类 自定义元类 元类实现ORM接口类与抽象类抽象…...

fuchsia系统介绍
fuchsia系统 Fuchsia,是由Google公司开发的继Android和Chrome OS之后的第三个系统,已在Github中公开的部分源码可以得知。Google对于Fuchsia的说明是“Pink(粉红)Purple(紫色)Fuchsia(灯笼海棠…...

解决Jenkins执行Python脚本不能实时输出打印信息的问题
问题: 在使用Jenkins的shell command来执行python脚本时,总是会等脚本执行完毕,最后一次性才把脚本中的print语句给打印出来; 解决方法: 在print语句后加上sys.stdout.flush(), 就可以达到实时输出的目的了。...

2021年03月 C/C++(五级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:最小新整数 给定一个十进制正整数n(0 < n < 1000000000),每个数位上数字均不为0。n的位数为m。 现在从m位中删除k位(0<k < m),求生成的新整数最小为多少? 例如: n = 9128456, k = 2, 则生成的新整数最小为12456 时间…...
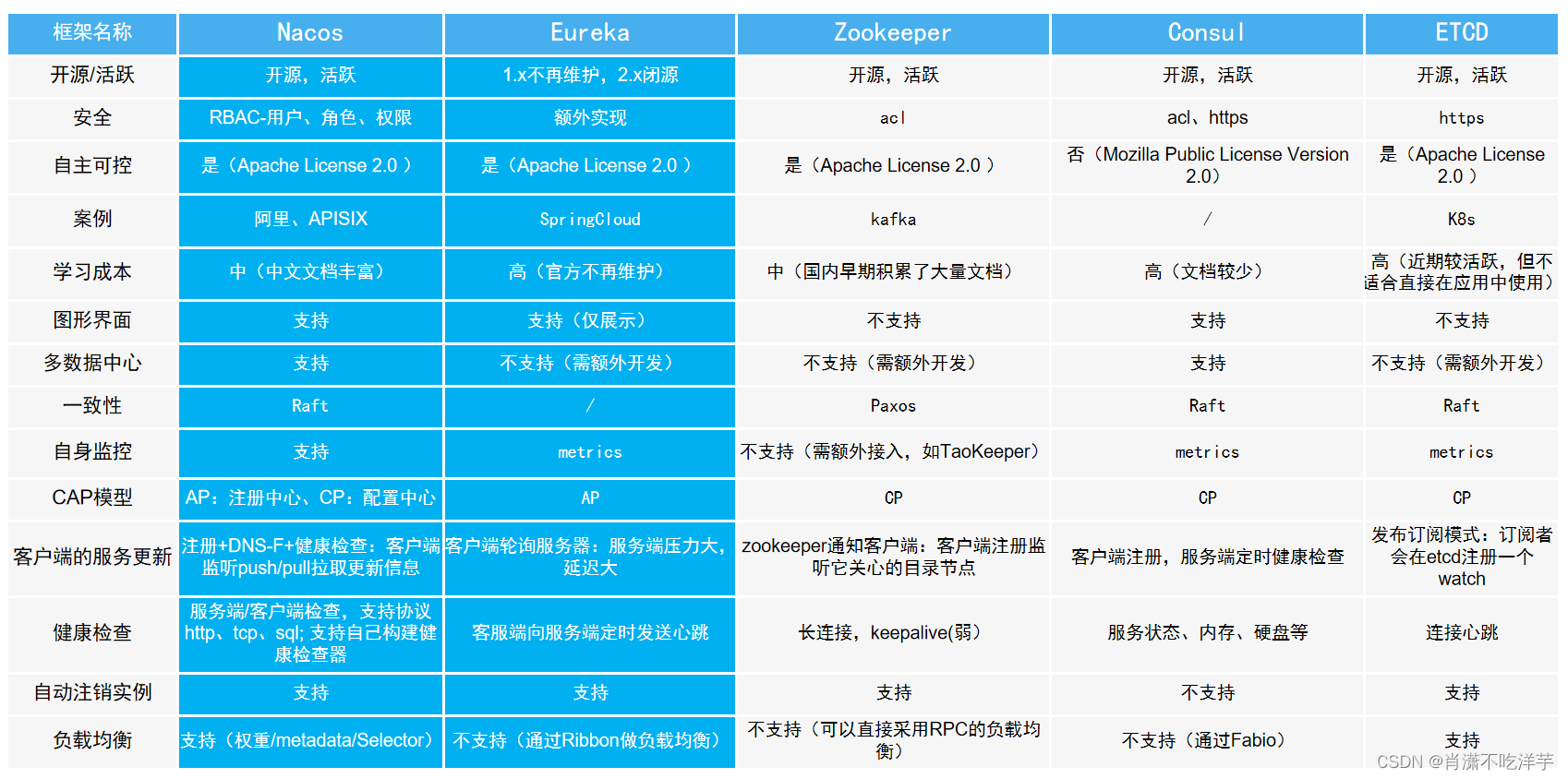
【微服务】服务发现和管理技术框架选型调研
选型背景 方案对比 结论 结合实际业务和开发需要,着重考虑性能可靠性、功能和社区支持程度三方面,认为Nacos更适合作为服务发现和管理的技术框架。具体理由如下: 性能更好,可靠性更高 经过阿里、APISIX、SpringCloudAlibaba,阿…...
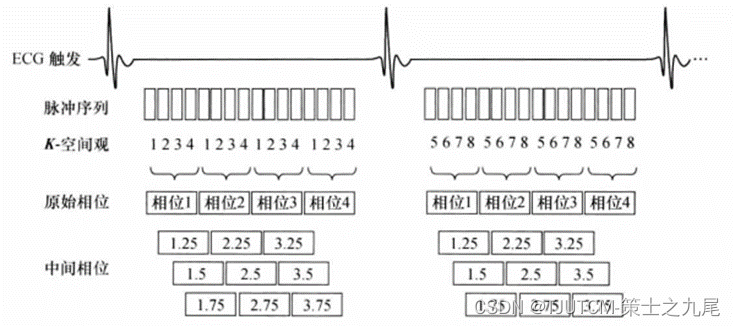
【核磁共振成像】观共享重建
目录 一、K空间关键孔技术-数据采集二、BRISK技术三、TRICKS技术四、实时成像和滑动窗重建五、心电触发电影(CINE)采集六、分段心脏采集和观共享 一、K空间关键孔技术-数据采集 对于笛卡尔K空间,一个相位编码行有时称为一个K空间观。一般情况下,每帧图像…...

〔020〕Stable Diffusion 之 骨骼姿势 篇
✨ 目录 🎈 姿势检测 / OpenPose🎈 姿势检测 OpenPose 参数介绍🎈 姿势检测 OpenPose 基本使用🎈 深度库 / Depth Lib🎈 深度库 Depth Lib 参数介绍🎈 3D姿势检测 / 3D Openpose Editor🎈 3D姿势检测 3D Openpose Editor 参数介绍🎈 3D姿势检测 3D Openpose Ed…...

使用Python进行Base64编码和解码
假设您有一个想要通过网络传输的二进制图像文件。您很惊讶对方没有正确接收该文件 - 该文件只是包含奇怪的字符! 嗯,您似乎试图以原始位和字节格式发送文件,而所使用的媒体是为流文本而设计的。 避免此类问题的解决方法是什么?答…...

MongoDB的数据恢复与备份
MongoDB的数据恢复与备份 在MongoDB中,备份和恢复数据是一项关键任务,可以确保数据的安全性并防止意外数据丢失。本文将介绍MongoDB的数据恢复与备份原理并提供相关的编程代码和配置。 1. 数据备份原理 MongoDB提供了多种备份数据…...
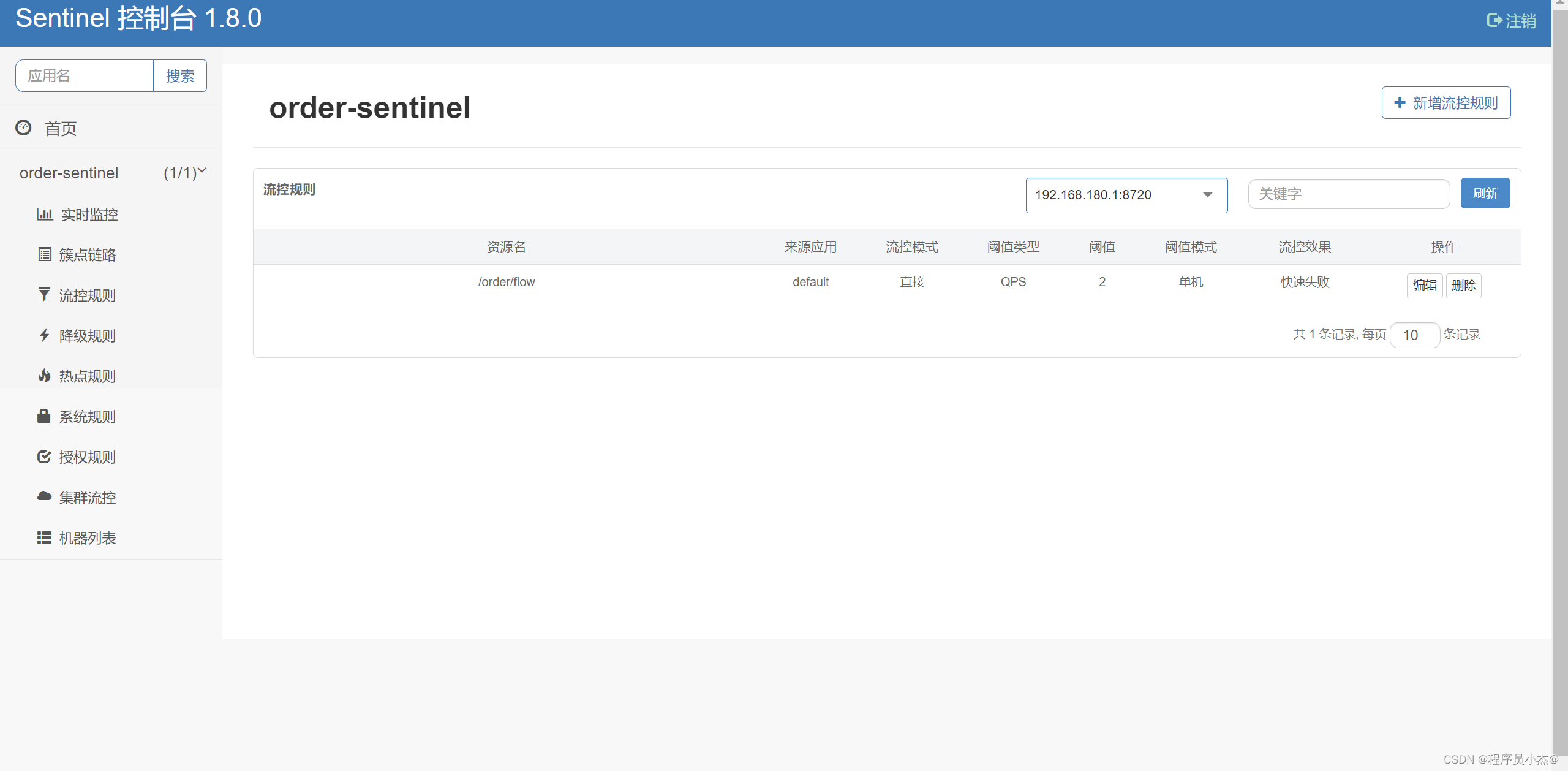
Java之SpringCloud Alibaba【五】【微服务 Sentinel整合openfeign进行降级】
一、Sentinel整合openfeign 1、复制一下order-openfeign项目(创建order-openfeign-sentinel) 然后在stock-nacos当中编写对应的接口 RequestMapping("/reduct2")public String reduct2(){int a 1/0;System.out.println("扣减库存"…...
电脑前置耳机没声音怎么办
有很多小伙伴反映在将自己的耳机连接到主机前面时没有声音,这是怎么回事呢,遇到这种情况应该怎么解决呢,下面小编就给大家详细介绍一下电脑前置耳机没声音的解决方法,有需要的小伙伴可以来看一看电脑前面耳机没声音。 解决方法&a…...

package.json 详解
文章目录 package.json1. name2. version3. description4. homepage5. bugs6. license7. author, contributors8. funding9. files10. main11. module12. browser13. bin14. man15. directories15.1 directories.bin15.2 directories.man 16. repository17. scripts18. config1…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...
