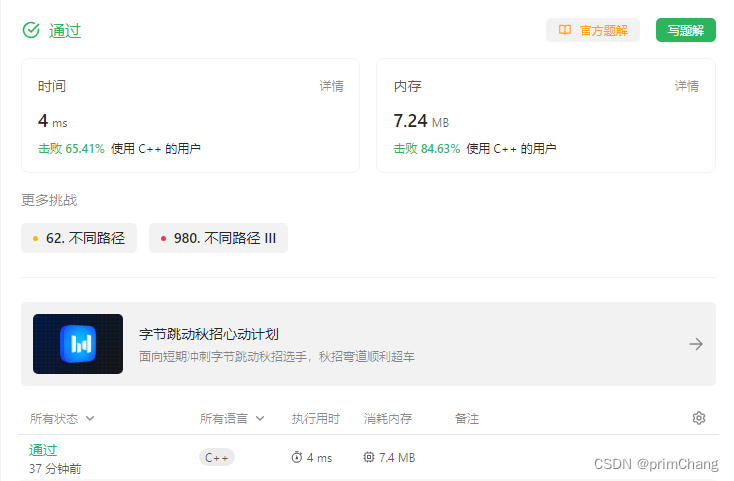
leetCode动态规划“不同路径II”
迷宫问题是比较经典的算法问题,一般可以用动态规划、回溯等方法进行解题,这道题目是我昨晚不同路径这道题趁热打铁继续做的,思路与原题差不多,只是有需要注意细节的地方,那么话不多说,直接上coding和解析!
题目描述
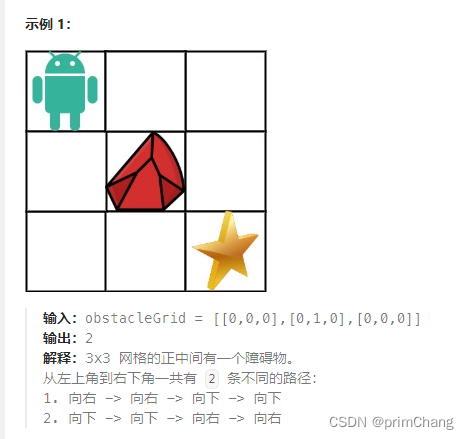
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
解析
如果做过类似迷宫问题的读者,对于这道题目的思路想必也会第一时间想到仍然使用动态规划的思路去解答,但是对于路径中的障碍物在这里却需要着重的单独讨论,因为有了障碍物,那么对于部分目标点的路径数会发生改变。此题目中需要考虑的特殊位置有如下图所示;
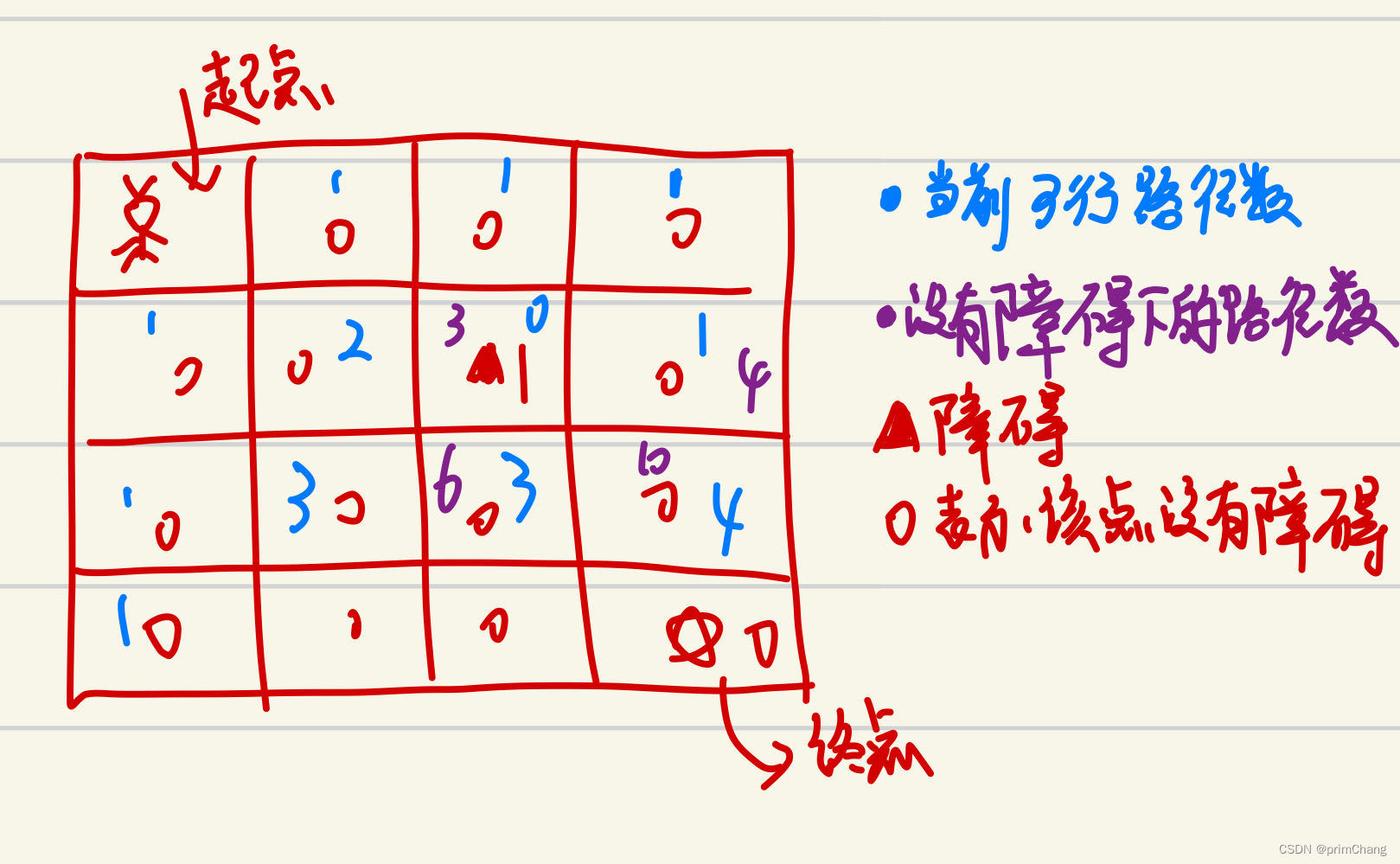
所画图给出了一种情况下的各个点下的路径数,可以看到,对于紫色笔给出的新的当前的节点路径数,仍满足原始状态下的dp[i][j] = dp[i-1][j]+dp[i][j-1]的动态递推式(但对于有障碍的节点不满足,那么障碍节点可达到路径数直接为0),对于迷宫问题,当前节点的可通行路线是由当前节点的左侧节点和正上方节点的可通过路径数相加得到,那对于左上方存在障碍的情况,当前节点的可通过数就需要变化。如下图所示。
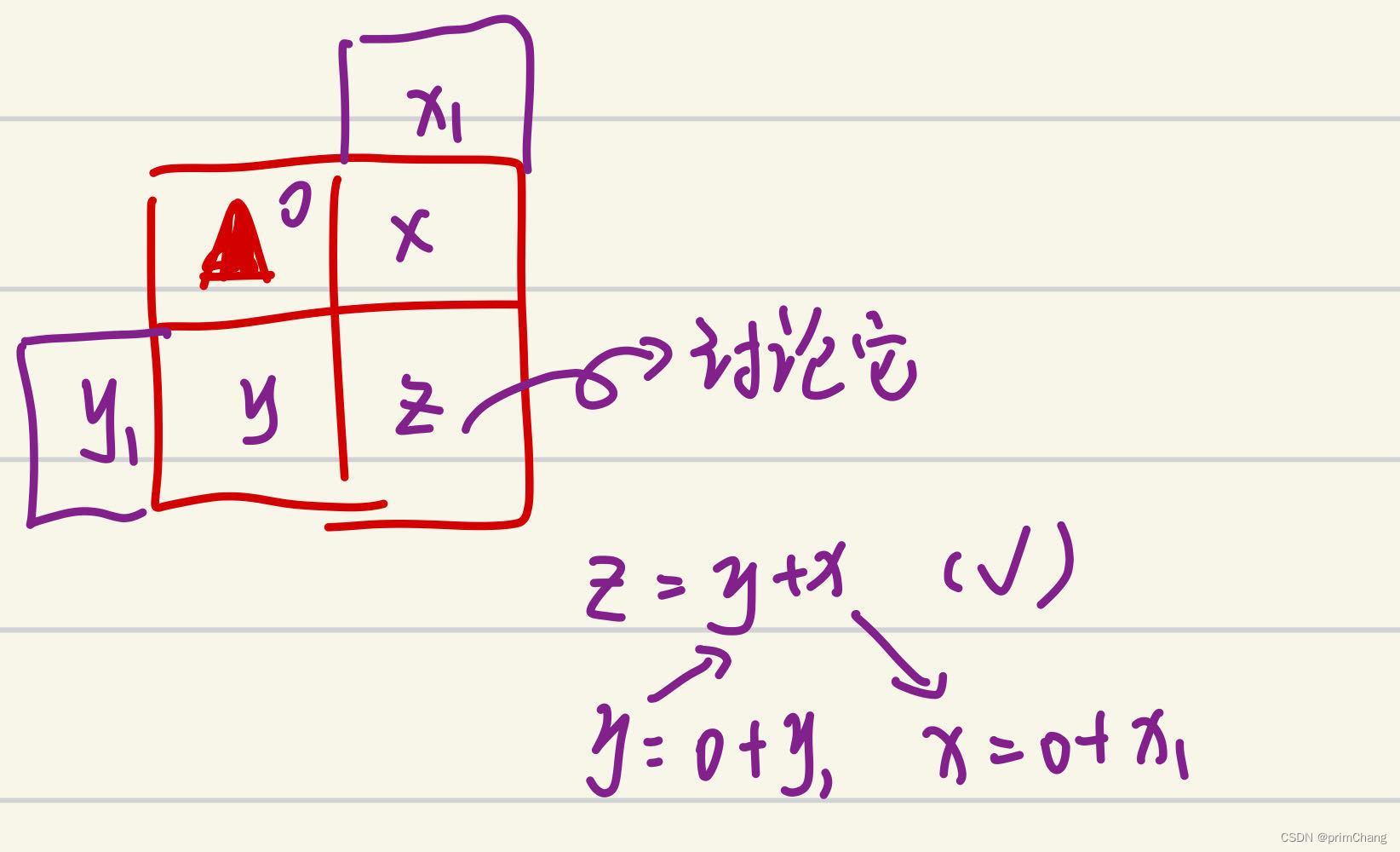
这是相对于原始题目的第一处变化,考虑了障碍物,那么就得讨论一下障碍物在某些特殊位置下的特殊情况,比如障碍物在初始行、列上的时候,比如:
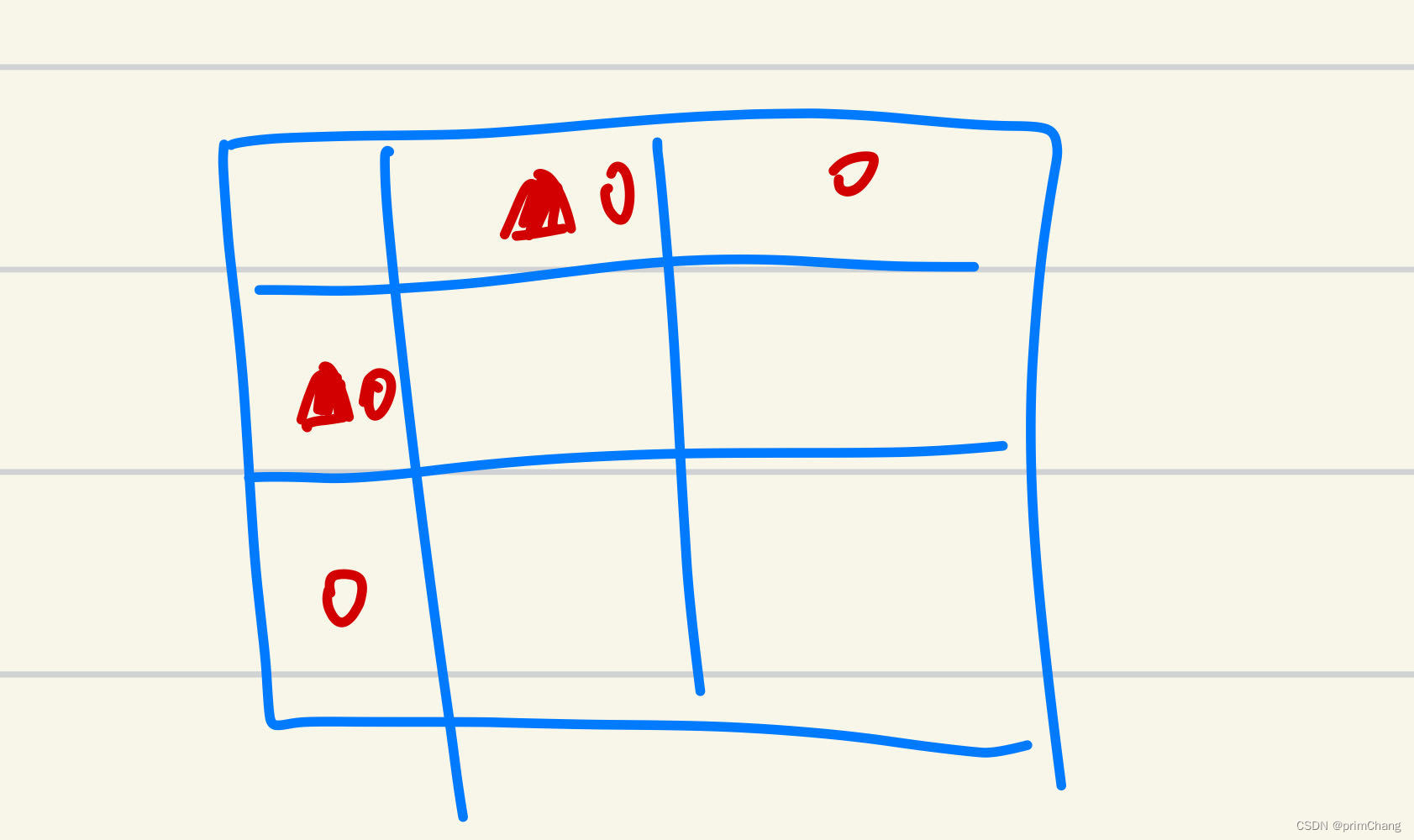
这种情况下,我们就不能单纯的只能把障碍物所处的位置上的路径数置为0,而是要把往后的那一列/一行上的数据都要置为0,为什么,因为机器人只能向下或者向右走,所以,对于初始行、列上的障碍物往后的点,机器人是无法到达的!!!
当然,还剩下最后一个情况,起点就有障碍物,那直接return 0咯~
代码
1.初始化dp数组
//初始化dp数组,我这里全给的-1,方便后续判别障碍物、无障碍物和路径数
int dp[110][110];for(int i=0;i<110;i++){for(int j =0;j<110;j++){dp[i][j] = -1;}}
2.根据地图,将地图中障碍物所处对应的dp数组位置置路径数为0
for(int i=0;i<obstacleGrid.size();i++){for(int j=0;j<obstacleGrid[i].size();j++){if(i == 0 && j ==0){//起点是障碍物if(obstacleGrid[i][j] == 1){return 0;}}if(i == 0){//障碍物在初始行上if(obstacleGrid[i][j] == 1){for(int m = j;m<obstacleGrid[i].size();m++){dp[i][m] = 0;}}}if(j == 0){//障碍物在初始列上if(obstacleGrid[i][j] == 1){dp[i][j] = 0;for(int x = i+1;x<obstacleGrid.size();x++){dp[x][j] = 0;}}}else if(i != 0 && j!= 0){//障碍物不在特殊位置上,那直接对应位置dp设置为0即可if(obstacleGrid[i][j] == 1){dp[i][j] = 0;}}}}
3.计算dp数组
for(int i=0;i<obstacleGrid.size();i++){for(int j=0;j<obstacleGrid[i].size();j++){if(i == 0 || j == 0){if(dp[i][j] == -1){dp[i][j] = 1;}}if(i != 0 && j != 0){if(dp[i][j] != 0){dp[i][j] = dp[i-1][j] + dp[i][j-1];}}}}
4. 完整代码和结果
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {// 跟第一种情况是一样的,只是对于地图中有障碍物的地方,对应的dp数组置为1int dp[110][110];for(int i=0;i<110;i++){for(int j =0;j<110;j++){dp[i][j] = -1;}}for(int i=0;i<obstacleGrid.size();i++){for(int j=0;j<obstacleGrid[i].size();j++){if(i == 0 && j ==0){if(obstacleGrid[i][j] == 1){return 0;}}if(i == 0){if(obstacleGrid[i][j] == 1){for(int m = j;m<obstacleGrid[i].size();m++){dp[i][m] = 0;}// break;}}if(j == 0){if(obstacleGrid[i][j] == 1){dp[i][j] = 0;for(int x = i+1;x<obstacleGrid.size();x++){dp[x][j] = 0;}// break;}}else if(i != 0 && j!= 0){if(obstacleGrid[i][j] == 1){dp[i][j] = 0;}}}}for(int i=0;i<obstacleGrid.size();i++){for(int j=0;j<obstacleGrid[i].size();j++){if(i == 0 || j == 0){if(dp[i][j] == -1){dp[i][j] = 1;}}if(i != 0 && j != 0){if(dp[i][j] != 0){dp[i][j] = dp[i-1][j] + dp[i][j-1];}}// else{// dp[i][j] = dp[i-1][j] + dp[i][j-1];// }}}cout<<dp[obstacleGrid.size()-1][obstacleGrid[0].size()-1];return dp[obstacleGrid.size()-1][obstacleGrid[0].size()-1];}
};
总结
个人感觉,这类题目是十分具有代表性的动态规划算法题 ,为什么这么说,因为动态规划要满足最优子结构,而恰恰这类题的子结构十分清晰,就比如我要知道当前位置有几种路径可以到达,就可以直接从我的前一步,也就是我的左边那一步和正上面的那一步就能到达,也就是我的左边和上面是与我当前可联通的,那么就直接得到了我当前的可通行路径数。有的人可能会说,那这样的话,应该是两者之和再加1才是最终的路径数呀?
其实不然,我最开始也陷入了这样的思维模式中去了,而其实应该这么想,我们所要求的是路径,而不是步数,讨论的不是走了几步,而是有几种到达的方法,换言之就是,只要我能到达左边那个位置或者上面那个位置,那么我一定能够到达当前所求的这个位置,那么也就说明,到达上面/左边位置的路径均能到达我当前的位置,那么两个地方的路径数之和就是到达当前位置的路径数之和~ 这里就不贴图了 ,如果文字描述不清楚,可以结合上面的xyz那张图(也就是所有图中的第三张图)进行结合理解。
动态规划变种很多,前些时候做了些公司面试笔试题 ,发现很多题可以用动态规划来做,但是不得其解,文中的题目是比较清晰的,容易推出动态规划递推式的类型,对于一些变种,还需要多做多总结!欢迎各位读者在评论区进行讨论,有更好的方法我也很愿意与您交流学习!
如果文章对您有帮助,可以点个小赞哦~
相关文章:

leetCode动态规划“不同路径II”
迷宫问题是比较经典的算法问题,一般可以用动态规划、回溯等方法进行解题,这道题目是我昨晚不同路径这道题趁热打铁继续做的,思路与原题差不多,只是有需要注意细节的地方,那么话不多说,直接上coding和解析&a…...

100天精通Python(可视化篇)——第99天:Pyecharts绘制多种炫酷K线图参数说明+代码实战
文章目录 专栏导读一、K线图介绍1. 说明2. 应用场景 二、配置说明三、K线图实战1. 普通k线图2. 添加辅助线3. k线图鼠标缩放4. 添加数据缩放滑块5. K线周期图表 书籍推荐 专栏导读 🔥🔥本文已收录于《100天精通Python从入门到就业》:本专栏专…...

哈希表与有序表
哈希表与有序表 Set结构 key Map结构 key-value 哈希表 哈希表的时间复杂度都是常数项级别的,但常数较大 增删改查的时间都是常数级别的,与数据量无关 当哈希表存储的值是基础数据类型(Integer - int),哈希表中内…...

什么时候使用RPA?如何使用RPA?需要什么样的硬件支持?需要安装哪些软件?
RPA(Robotic Process Automation)是一种用于自动化执行重复性任务的技术,它可以帮助企业提高工作效率,降低人力成本,并减少人为错误。RPA适用于各种行业和场景,例如财务、人力资源、客户服务、IT运维等。 …...
R语言入门——line和lines的区别
目录 0 引言一、 line()二、 lines() 0 引言 首先,从直观上看,lines比line多了一个s,但它们还是有很大的区别的,下面将具体解释这个两个函数的区别。 一、 line() 从R语言的帮助文档中找到,line()的使用,…...
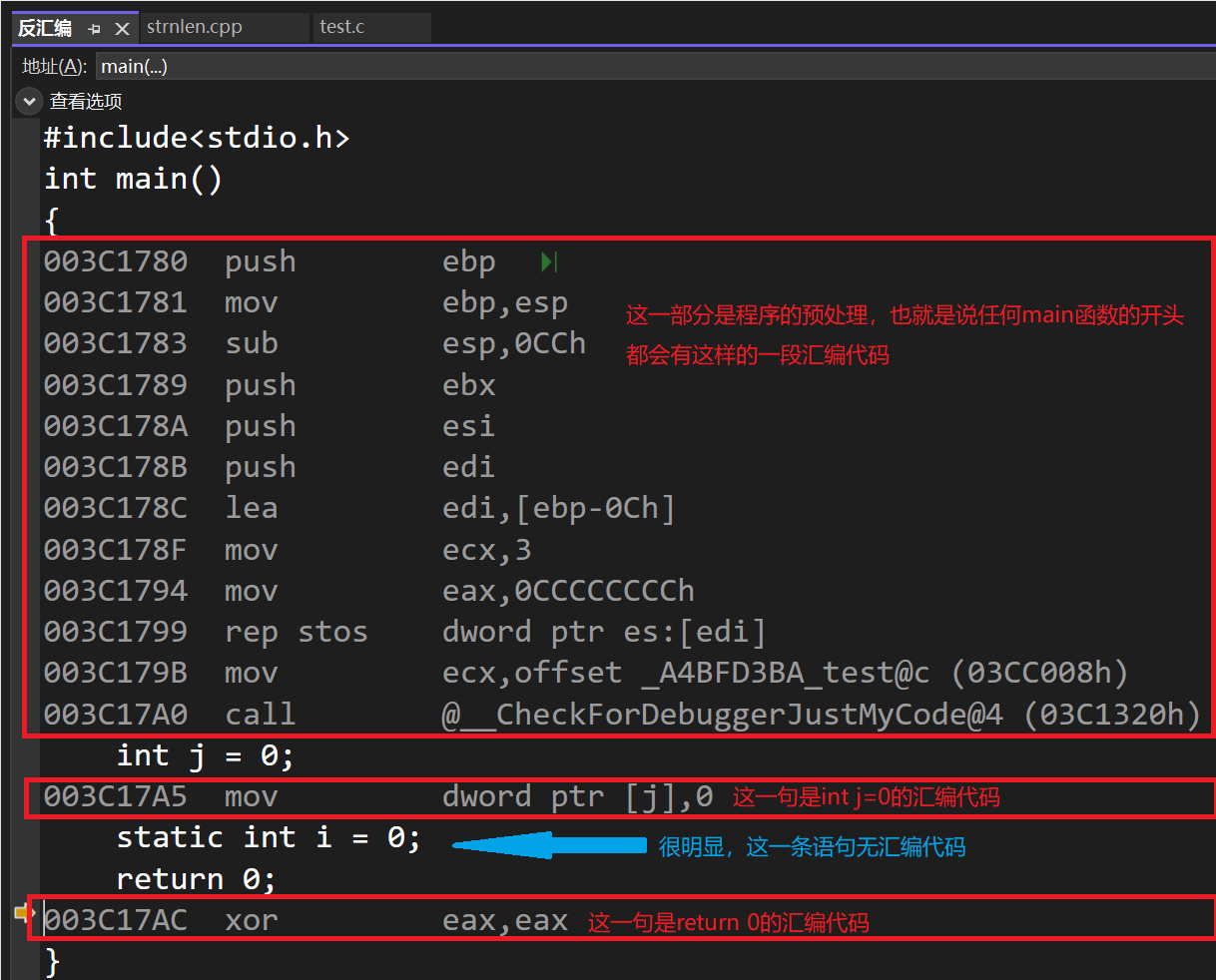
C语言:static关键字的使用
1.static修饰局部变量 这是static关键字使用最多的情况。我们知道局部变量是在程序运行阶段在栈上创建的,但是static修饰的局部变量是在程序编译阶段在代码段(静态区)创建的。所以在static修饰的变量所在函数执行结束后该变量依然存在。 //…...
:ECUM的ISOLAR-AB配置及代码解析)
AUTOSAR知识点 之 ECUM (三):ECUM的ISOLAR-AB配置及代码解析
目录 1、概述 2、ISOLAR-AB配置 2.1、EcuMGeneral 2.2、EcuMConfiguration 2.2.1、EcuMDefaultShutdownTarget 2.2.2、EcuMDriverInitListOne...
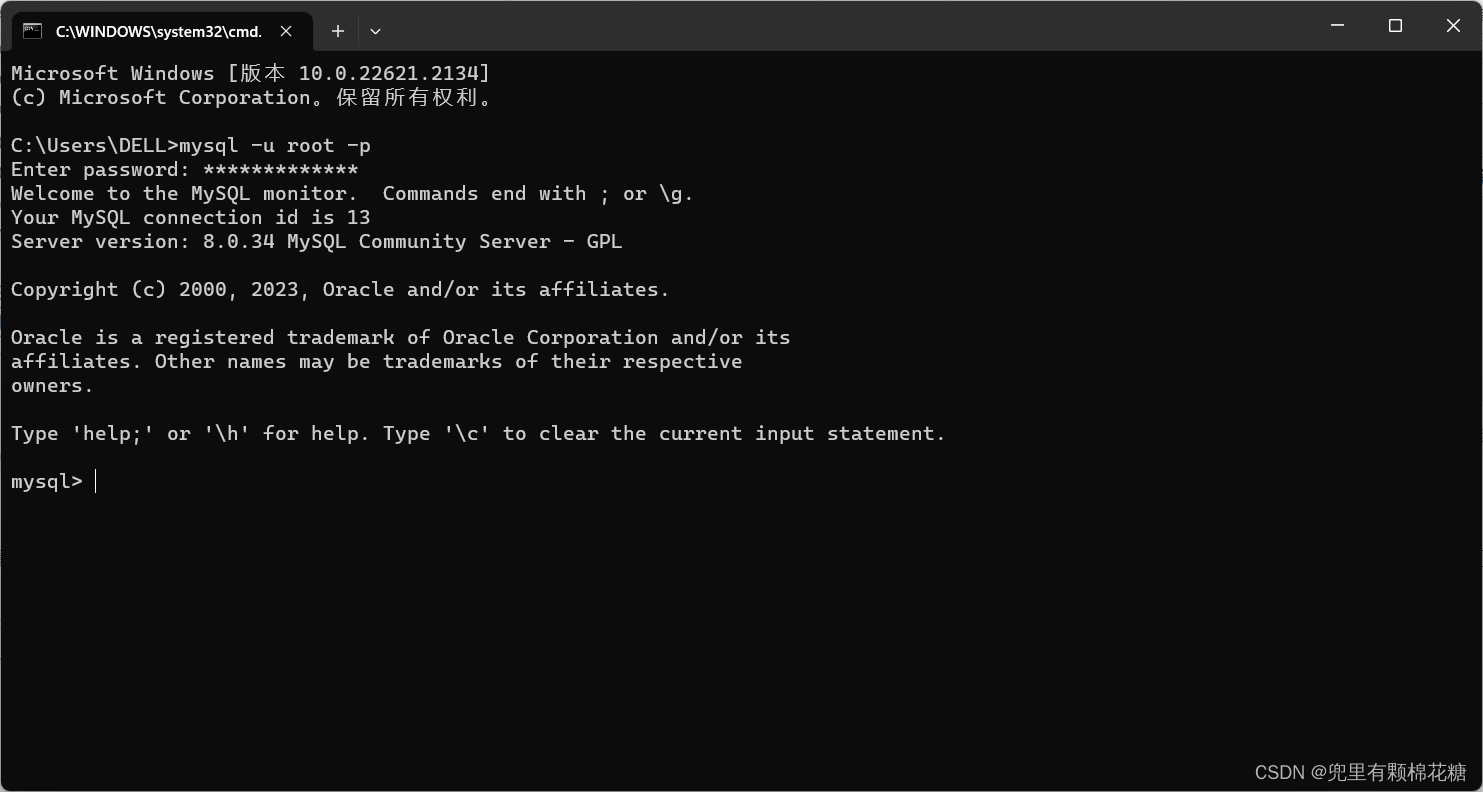
2023年MySQL-8.0.34保姆级安装教程
重点放前面:演示环境为windows环境。 MySQL社区版本安装教程如下: 一、MySQL安装包下载二、安装配置设置三、配置环境变量 大体分为3个步骤:①安装包的下载;②安装配置设置;③配置环境变量 一、MySQL安装包下载 下载官…...
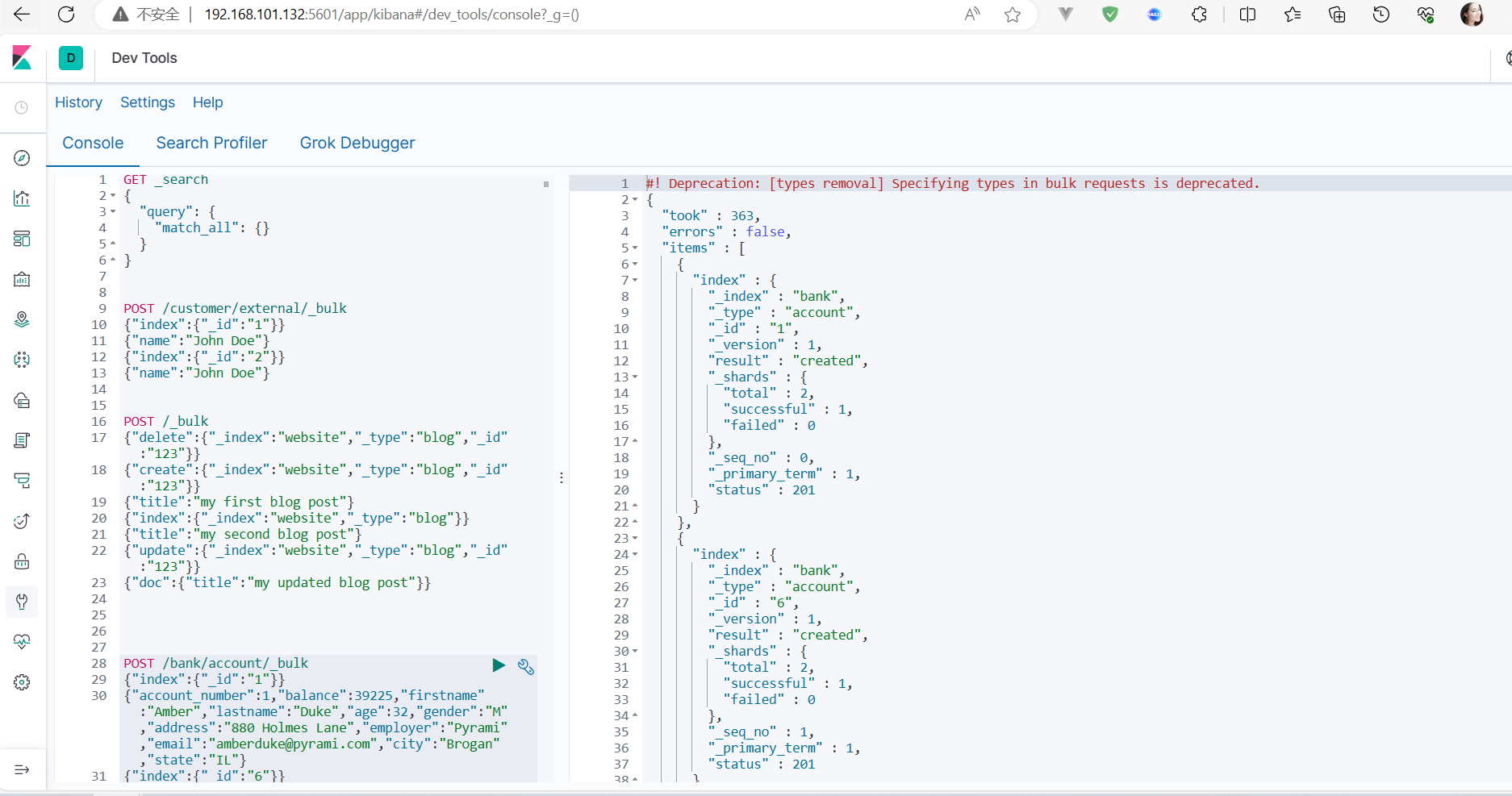
ElasticSearch入门
一、基本命令_cat 1、查看节点信息 http://192.168.101.132:9200/_cat/nodes2、查看健康状况 http://192.168.101.132:9200/_cat/health3、查看主节点的信息 http://192.168.101.132:9200/_cat/master4、查看所有索引 http://192.168.101.132:9200/_cat/indices二、索引一…...

RocketMQ的Broker
1 Broker角色 Broker角色分为ASYNC_MASTER (异步主机)、SYNC_MASTER (同步主机)以及SLAVE (从机)。如果对消息的可靠性要求比较严格,可以采用SYNC_MASTER加SLAV E的部署方式。如果对消息可靠性要求不高,可以采用ASYNC_MASTER加ASL AVE的部署方式。如果只…...

使用Puppeteer进行游戏数据可视化
导语 Puppeteer是一个基于Node.js的库,可以用来控制Chrome或Chromium浏览器,实现网页操作、截图、测试、爬虫等功能。本文将介绍如何使用Puppeteer进行游戏数据的爬取和可视化,以《英雄联盟》为例。 概述 《英雄联盟》是一款由Riot Games开…...

【Flask】from flask_sqlalchemy import SQLAlchemy报错
【可能出现的情况】 1、未安装 Flask-SQLAlchemy: 在使用 flask_sqlalchemy 之前,你需要确保已经通过 pip 安装了 Flask-SQLAlchemy。可以通过以下命令安装它: pip install Flask-SQLAlchemy 2、包名大小写问题: Python 是区分大…...

索引简单概述(SQL)
一、什么是索引? 索引是一种特殊的文件(InnoDB数据表上的索引是表空间的一个组成部分),他们包含着对数据表里所有记录的引用指针。 索引是一种数据结构。数据库索引,是数据库管理系统中一个排序的数据结构࿰…...

union all 和 union 的区别,mysql union全连接查询
602. 好友申请 II :谁有最多的好友(力扣mysql题,难度:中等) RequestAccepted 表: ------------------------- | Column Name | Type | ------------------------- | requester_id | int | | accepter_id | int | | accept_date …...

UDP和TCP的区别
UDP (User Datagram Protocol) 和 TCP (Transmission Control Protocol) 是两种常见的传输层协议。它们在设计和用途上有很大的区别,以下是它们的主要差异: 连接性: TCP: 是一个连接导向的协议。它首先需要建立连接,数据传输完毕后再终止连接…...

阿里云 MSE 助力开迈斯实现业务高增长背后带来的服务挑战
开迈斯新能源科技有限公司于 2019 年 5 月 16 日成立,目前合资股东分别为大众汽车(中国)投资有限公司、中国第一汽车股份有限公司、一汽-大众汽车有限公司[增资扩股将在取得适当监督(包括反垄断)审批后完成]、万帮数字…...

消灭怪物的最大数量【力扣1921】
一、题目分析 需要满足的条件: 只能在每分钟的开始使用武器武器能杀死距离城市最近的怪兽怪兽到达城市就会输掉游戏 游戏最优策略:我们可以在每分钟的开始都使用一次武器,用来杀死距离城市最近的怪兽。这样可以在力所能及的范围内…...

数据结构之算法
算法的基本概念 计算机解题的过程实际上是在实施某种算法,这种算法称为计算机算法 算法的基本要素 一个算法是由两种基本要素组成:一是对数据对象的运算和操作;二是算法的控制结构 算法中对数据的运算和操作 在一般计算机系统中…...

MyBatis与MyBatis-Plus的分页以及转换
一、介绍 MyBatis和MyBatis-Plus都是Java持久化框架,用于简化数据库访问和操作。它们提供了面向对象的方式来管理关系型数据库中的数据。 MyBatis是一个轻量级的持久化框架,通过XML或注解配置,将SQL语句与Java对象进行映射,使开…...
 套接字协议及其数据传输特性)
TCP/IP网络编程(二) 套接字协议及其数据传输特性
文章目录 套接字协议及其数据传输特性关于协议创建套接字协议族套接字类型1:面向连接的套接字(SOCK_STREAM)套接字类型2:面向消息的套接字(SOCK_DGRAM)协议的最终选择面向连接的套接字:TCP套接字…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
